{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Probability Distribution\n",
    "\n",
    "확률 분포"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<style>.container { width:100% !important; }</style>"
      ],
      "text/plain": [
       "<IPython.core.display.HTML object>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "python ver=3.8.9 (default, Jun 27 2021, 02:41:12) \n",
      "[GCC 7.5.0]\n",
      "pandas ver=1.2.5\n",
      "numpy ver=1.19.5\n",
      "scipy ver=1.6.3\n"
     ]
    }
   ],
   "source": [
    "# 경고 메시지 출력 끄기\n",
    "import warnings \n",
    "warnings.filterwarnings(action='ignore')\n",
    "\n",
    "# 노트북 셀 표시를 브라우저 전체 폭 사용하기\n",
    "from IPython.core.display import display, HTML\n",
    "display(HTML(\"<style>.container { width:100% !important; }</style>\"))\n",
    "from IPython.display import clear_output\n",
    "\n",
    "%matplotlib inline\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "import os, sys, shutil, functools\n",
    "import collections, pathlib, re, string\n",
    "\n",
    "rseed = 22\n",
    "import random\n",
    "random.seed(rseed)\n",
    "\n",
    "import numpy as np\n",
    "np.random.seed(rseed)\n",
    "np.set_printoptions(precision=5)\n",
    "np.set_printoptions(formatter={'float_kind': \"{:.5f}\".format})\n",
    "\n",
    "import pandas as pd\n",
    "pd.set_option('display.max_rows', None) \n",
    "pd.set_option('display.max_columns', None) \n",
    "pd.set_option('display.max_colwidth', None)\n",
    "pd.options.display.float_format = '{:,.5f}'.format\n",
    "\n",
    "import scipy as sp\n",
    "\n",
    "import seaborn as sns\n",
    "\n",
    "from pydataset import data\n",
    "\n",
    "print(f\"python ver={sys.version}\")\n",
    "print(f\"pandas ver={pd.__version__}\")\n",
    "print(f\"numpy ver={np.__version__}\")\n",
    "print(f\"scipy ver={sp.__version__}\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "<class 'pandas.core.frame.DataFrame'>\n",
      "Int64Index: 150 entries, 1 to 150\n",
      "Data columns (total 5 columns):\n",
      " #   Column        Non-Null Count  Dtype  \n",
      "---  ------        --------------  -----  \n",
      " 0   Sepal.Length  150 non-null    float64\n",
      " 1   Sepal.Width   150 non-null    float64\n",
      " 2   Petal.Length  150 non-null    float64\n",
      " 3   Petal.Width   150 non-null    float64\n",
      " 4   Species       150 non-null    object \n",
      "dtypes: float64(4), object(1)\n",
      "memory usage: 7.0+ KB\n"
     ]
    }
   ],
   "source": [
    "# Iris 데이터 셋의 컬럼 정보 살피기\n",
    "df_iris = data('iris')\n",
    "df_iris.info()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 확률과 확률 분포 (Probability and Probability Distribution)\n",
    "\n",
    "주사위를 실제 던져보기 전까지는 주사위의 어떤 수가 나오게 될지 알수 없지만 주사위를 던졌을 때 각 수가 나오는 가능성은 1/6 으로 예측 할 수 있습니다. 추측 통계에서는 결과 예측시 확률과 확률의 분포를 이용합니다.\n",
    "\n",
    "* 사상: 시행 (실험, 관측 등)에 의해 생긴 결과 (주사위 예에서는 던져서 나온 수)\n",
    "* 확률: 사상이 어느정도 일어나기 쉬운지를 수치화, 모든 사상의 합은 1 (주사위 예에서는 각 눈의 확률)\n",
    "* 확률변수: 시행해 봐야 결과를 알 수 있는 변수를 확률 변수라 정의\n",
    "  * 이산확률변수: 변수가 취할 수 있는 값이 이산형인 확률 변수 (예, 주사위, 동전 등)\n",
    "  * 연속확률변수: 변수가 취할 수 있는 값이 연속형인 활률 변수 (예, 키, 몸무게 등)\n",
    "* 확률분포: 확률 변수(전체 합 = 1)가 취할 수 있는 값이 어떻게 분포하고 있는지 나타냄\n",
    "\n",
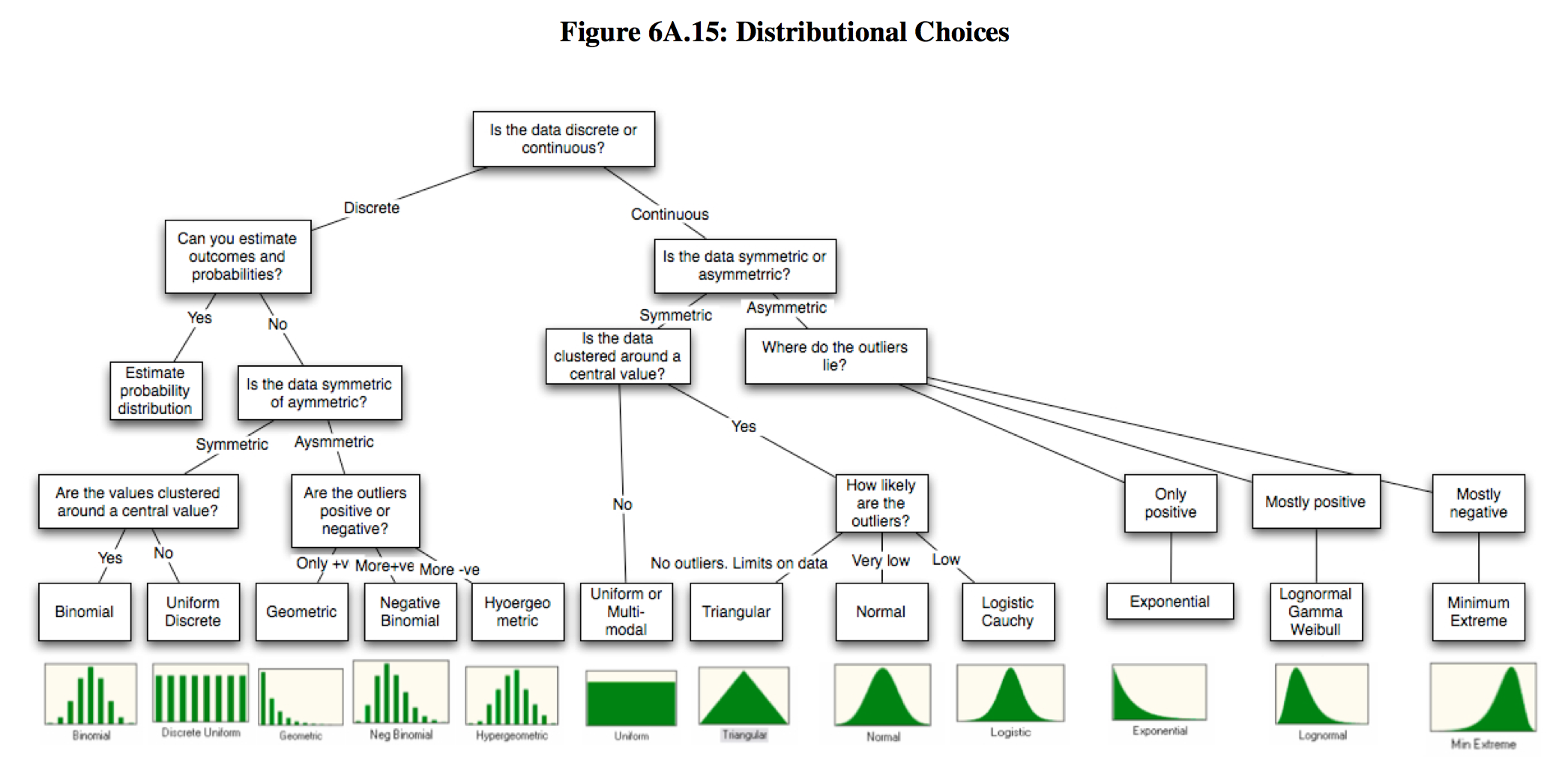    "![](https://tinyheero.github.io/assets/prob-distr/overview-prob-distr.png)\n",
    "\n",
    "https://tinyheero.github.io/2016/03/17/prob-distr.html\n",
    "\n",
    "**Further Reading**\n",
    "* [Probability Distributions in Python Tutorial](https://www.datacamp.com/community/tutorials/probability-distributions-python)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "**도수분포표 (Frequency Distribution Table)**\n",
    "\n",
    "도수분포표는 데이터를 계급으로 나누고 계급에 대한 빈도를 세어 표시하는 테이블입니다. 범주형 변수의 경우는 간단하게 구할 수 있지만, 연속형 변수의 경우에는 어떻게 계급을 나누어 표시해야 하는지에 대한 어려운 부분이 존재합니다. \n",
    "\n",
    "연속형 변수의 적장한 계급 수를 구하는 방법은 주로 Sturge’s rule 또는 Freedman-Diaconis rule 을 사용합니다.\n",
    "\n",
    "**Sturge's rule**\n",
    "\n",
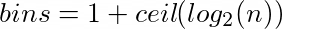    "![](https://miro.medium.com/max/324/1*E2cFPT9fMhdF74FVANGchQ.png)\n",
    "\n",
    "**Freedman-Diaconis rule**\n",
    "\n",
    "![](https://miro.medium.com/max/409/1*K04B59josTwu3Yp2acpfmA.png)\n",
    "\n",
    "https://medium.datadriveninvestor.com/how-to-decide-on-the-number-of-bins-of-a-histogram-3c36dc5b1cd8\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th>col_0</th>\n",
       "      <th>frequency</th>\n",
       "      <th>cumulative_frequency</th>\n",
       "      <th>relative_frequency</th>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>Species</th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>setosa</th>\n",
       "      <td>50</td>\n",
       "      <td>50</td>\n",
       "      <td>0.33333</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>versicolor</th>\n",
       "      <td>50</td>\n",
       "      <td>100</td>\n",
       "      <td>0.33333</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>virginica</th>\n",
       "      <td>50</td>\n",
       "      <td>150</td>\n",
       "      <td>0.33333</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "col_0       frequency  cumulative_frequency  relative_frequency\n",
       "Species                                                        \n",
       "setosa             50                    50             0.33333\n",
       "versicolor         50                   100             0.33333\n",
       "virginica          50                   150             0.33333"
      ]
     },
     "execution_count": 3,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df_iris = data('iris')\n",
    "\n",
    "# 범주형 변수의 도수 분포표\n",
    "fdt = pd.crosstab(index=df_iris['Species'], columns='frequency')\n",
    "fdt['cumulative_frequency'] = fdt['frequency'].cumsum() # 누적도수\n",
    "fdt['relative_frequency'] = fdt['frequency'] / fdt['frequency'].sum() # 상대도수\n",
    "fdt"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th>col_0</th>\n",
       "      <th>frequency</th>\n",
       "      <th>cumulative_frequency</th>\n",
       "      <th>relative_frequency</th>\n",
       "      <th>cumulative_relative_frequency</th>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>Sepal.Length</th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "      <th></th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>[4.3, 4.7)</th>\n",
       "      <td>9</td>\n",
       "      <td>9</td>\n",
       "      <td>0.06000</td>\n",
       "      <td>0.06000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[4.7, 5.1)</th>\n",
       "      <td>23</td>\n",
       "      <td>32</td>\n",
       "      <td>0.15333</td>\n",
       "      <td>0.21333</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[5.1, 5.5)</th>\n",
       "      <td>20</td>\n",
       "      <td>52</td>\n",
       "      <td>0.13333</td>\n",
       "      <td>0.34667</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[5.5, 5.9)</th>\n",
       "      <td>28</td>\n",
       "      <td>80</td>\n",
       "      <td>0.18667</td>\n",
       "      <td>0.53333</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[5.9, 6.3)</th>\n",
       "      <td>28</td>\n",
       "      <td>108</td>\n",
       "      <td>0.18667</td>\n",
       "      <td>0.72000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[6.3, 6.7)</th>\n",
       "      <td>14</td>\n",
       "      <td>122</td>\n",
       "      <td>0.09333</td>\n",
       "      <td>0.81333</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[6.7, 7.1)</th>\n",
       "      <td>17</td>\n",
       "      <td>139</td>\n",
       "      <td>0.11333</td>\n",
       "      <td>0.92667</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[7.1, 7.5)</th>\n",
       "      <td>5</td>\n",
       "      <td>144</td>\n",
       "      <td>0.03333</td>\n",
       "      <td>0.96000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>[7.5, 7.904)</th>\n",
       "      <td>6</td>\n",
       "      <td>150</td>\n",
       "      <td>0.04000</td>\n",
       "      <td>1.00000</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "col_0         frequency  cumulative_frequency  relative_frequency  \\\n",
       "Sepal.Length                                                        \n",
       "[4.3, 4.7)            9                     9             0.06000   \n",
       "[4.7, 5.1)           23                    32             0.15333   \n",
       "[5.1, 5.5)           20                    52             0.13333   \n",
       "[5.5, 5.9)           28                    80             0.18667   \n",
       "[5.9, 6.3)           28                   108             0.18667   \n",
       "[6.3, 6.7)           14                   122             0.09333   \n",
       "[6.7, 7.1)           17                   139             0.11333   \n",
       "[7.1, 7.5)            5                   144             0.03333   \n",
       "[7.5, 7.904)          6                   150             0.04000   \n",
       "\n",
       "col_0         cumulative_relative_frequency  \n",
       "Sepal.Length                                 \n",
       "[4.3, 4.7)                          0.06000  \n",
       "[4.7, 5.1)                          0.21333  \n",
       "[5.1, 5.5)                          0.34667  \n",
       "[5.5, 5.9)                          0.53333  \n",
       "[5.9, 6.3)                          0.72000  \n",
       "[6.3, 6.7)                          0.81333  \n",
       "[6.7, 7.1)                          0.92667  \n",
       "[7.1, 7.5)                          0.96000  \n",
       "[7.5, 7.904)                        1.00000  "
      ]
     },
     "execution_count": 4,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# 연속형 변수의 도수 분포표\n",
    "# Sturges's Rule 에 따른 Binning \n",
    "n_data = df_iris['Sepal.Length'].count()\n",
    "n_bins = int(np.ceil(np.log2(n_data) + 1))\n",
    "bins = pd.cut(x=df_iris['Sepal.Length'], bins=n_bins, right=False)\n",
    "fdt = pd.crosstab(index=bins, columns='frequency')\n",
    "fdt['cumulative_frequency'] = fdt['frequency'].cumsum() # 누적도수\n",
    "fdt['relative_frequency'] = fdt['frequency'] / fdt['frequency'].sum() # 상대도수\n",
    "fdt['cumulative_relative_frequency'] = fdt['relative_frequency'].cumsum() # 누적상대도수\n",
    "fdt"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "**히스토그램 (Histogram)**\n",
    "\n",
    "도수분포표를 통해 구한 계급 구간을 이용하여 히스토그램으로 데이터를 시각화 하여 살펴 봅니다. 히스토그램을 통한 데이터 시각화를 하면 좀 더 데이터 분포에 대하여 직관적으로 살펴볼 수 있습니다."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<AxesSubplot:>"
      ]
     },
     "execution_count": 5,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXIAAAD4CAYAAADxeG0DAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAOHklEQVR4nO3dbYxc5X2G8euu7TQJQYHULtlibKMIIVGpAbqipEQRLUlEqQWJiiqQSiEKMm1DG9pIheZDG/VTkPJS9UWkDtDQFmhSAo1rkRREI6FILaohLhicCEpszNbGJqhAX8Hm3w97TJbN7s54d2ZnHvv6SaM9c86zM7cfWfeeffbMTKoKSVK7fmTUASRJS2ORS1LjLHJJapxFLkmNs8glqXErl/PJVq9eXRs2bFjOp5Sk5j388MPPV9Wa+Y4va5Fv2LCBbdu2LedTSlLzkuxe6LhLK5LUOItckhpnkUtS4yxySWqcRS5JjbPIJalxFrkkNc4il6TGWeSS1LhlfWWnjj4Ta9exb2rPSDOseNObOfTK/440A8A7Tz6Fvc8+M+oYOgZZ5FqSfVN7WH/91pFm2H3jxpFnOJxDGgWXViSpcRa5JDXOIpekxlnkktQ4i1ySGmeRS1LjLHJJapxFLkmNs8glqXEWuSQ1ziKXpMZZ5JLUOItckhpnkUtS4yxySWqcRS5JjbPIJalxPYs8ySlJvpnkiSSPJ/l4t/9TSaaSbO9uFw0/riRptn4+6u0g8ImqeiTJ8cDDSe7vjn2+qj4zvHiSpF56FnlV7QX2dtsvJ9kJnDzsYJKk/hzRGnmSDcBZwEPdrmuTPJrk1iQnzvM9m5JsS7LtwIEDS0srSfohfRd5krcBXwWuq6qXgJuAdwFnMn3G/tm5vq+qNlfVZFVNrlmzZumJJUlv0FeRJ1nFdInfXlV3A1TVc1V1qKpeA74InDO8mJKk+fRz1UqAW4CdVfW5GfsnZgz7MLBj8PEkSb30c9XKecAVwGNJtnf7PglcnuRMoIBdwDVDyCdJ6qGfq1a+BWSOQ/cOPo4k6Uj5yk5JapxFLkmNs8glqXEWuSQ1ziKXpMZZ5JLUOItckhpnkUtS4yxySWqcRX6EJtauI8nIbxNr1416KiSNiX7ea0Uz7Jvaw/rrt446Brtv3DjqCJLGhGfkktQ4i1ySGmeRS1LjLHJJapxFLkmNs8glqXEWuSQ1ziKXpMZZ5JLUOItckhpnkUtS4yxySWqcRS5JjbPIJalxFrkkNc4il6TGWeSS1LieRZ7klCTfTPJEkseTfLzb/44k9yd5svt64vDjSpJm6+eM/CDwiao6AzgX+FiSM4AbgAeq6jTgge6+JGmZ9SzyqtpbVY902y8DO4GTgUuA27phtwEfGlJGSdICjujDl5NsAM4CHgJOqqq93aF9wEnzfM8mYBPAunV+8vvArFhFklGnkDQG+i7yJG8DvgpcV1UvzSyRqqokNdf3VdVmYDPA5OTknGO0CIdeZf31W0edgt03bhx1BOmY19dVK0lWMV3it1fV3d3u55JMdMcngP3DiShJWkg/V60EuAXYWVWfm3FoC3Blt30l8LXBx5Mk9dLP0sp5wBXAY0m2d/s+CXwa+EqSjwK7gV8eSkJJ0oJ6FnlVfQuY769qFww2jiTpSPnKTklqnEUuSY2zyCWpcRa5JDXOIpekxlnkktQ4i1ySGmeRS1LjLHJJapxFLkmNs8glqXEWuSQ1ziKXpMZZ5JLUOItckhpnkUtS4yxy6SgzsXYdSUZ+m1i7btRTcczo56PeJDVk39Qe1l+/ddQx2H3jxlFHOGZ4Ri5JjbPIJalxFrkkNc4il6TGWeSS1DiLXJIaZ5FLUuMscklqnEUuSY2zyCWpcT2LPMmtSfYn2TFj36eSTCXZ3t0uGm5MSdJ8+jkj/xJw4Rz7P19VZ3a3ewcbS5LUr55FXlUPAi8sQxZJ0iIsZY382iSPdksvJ843KMmmJNuSbDtw4MASnk6SNJfFFvlNwLuAM4G9wGfnG1hVm6tqsqom16xZs8inkyTNZ1FFXlXPVdWhqnoN+CJwzmBjSZL6tagiTzIx4+6HgR3zjZUkDVfPTwhKcidwPrA6ybPAHwDnJzkTKGAXcM3wIkqSFtKzyKvq8jl23zKELJKkRfCVnZLUOD98WRqUFatIMuoUOgZZ5NKgHHrVT6/XSLi0IkmNs8glqXEWuSQ1ziKXpMZZ5JLUOItckhpnkUtS4yxySWqcRS5JjbPIJalxFrkkNc4il6TGWeSS1DiLXJIaZ5FLUuMscklqnEUuSY2zyCWpcRa5JDXOIpekxlnkktQ4i1ySGmeRS1LjLHJJapxFLkmN61nkSW5Nsj/Jjhn73pHk/iRPdl9PHG5MSdJ8+jkj/xJw4ax9NwAPVNVpwAPdfUnSCPQs8qp6EHhh1u5LgNu67duADw02liSpX4tdIz+pqvZ22/uAk+YbmGRTkm1Jth04cGCRTydJms+S/9hZVQXUAsc3V9VkVU2uWbNmqU8nSZplsUX+XJIJgO7r/sFFkiQdicUW+Rbgym77SuBrg4kjSTpS/Vx+eCfwT8DpSZ5N8lHg08AHkjwJvL+7L0kagZW9BlTV5fMcumDAWSRJi+ArOyWpcT3PyMfFxNp17JvaM+oYkjR2minyfVN7WH/91lHHYPeNG0cdQZLewKUVSWqcRS5JjbPIJalxFrkkNc4il6TGWeSS1DiLXJIaZ5FLUuMscklqnEUuSY2zyCWpcRa5JDXOIpekxlnkktQ4i1ySGmeRS1LjLHJJapxFLkmNs8glqXEWuSQ1ziKXdFSbWLuOJCO/TaxdN7R/48qhPbIkjYF9U3tYf/3WUcdg940bh/bYnpFLUuMscklqnEUuSY1b0hp5kl3Ay8Ah4GBVTQ4ilCSpf4P4Y+fPVdXzA3gcSdIiuLQiSY1b6hl5AfclKeDPq2rz7AFJNgGbANatG951lJLGzIpVJBl1imPCUov8vVU1leTHgfuTfKeqHpw5oCv3zQCTk5O1xOeT1IpDrx7112+PiyUtrVTVVPd1P3APcM4gQkmS+rfoIk9yXJLjD28DHwR2DCqYJKk/S1laOQm4p1sDWwncUVXfGEgqSVLfFl3kVfU08O4BZpEkLYKXH0pS4yxySWqcRS5JjbPIJalxFrkkNc4il6TGWeSS1DiLXJIaZ5FLUuMscklqnEUuSY2zyCWpcRa5JDXOIpekxlnkktQ4i1ySGmeRS1LjLHJJapxFLkmNs8glqXEWuSQ1ziKXpMZZ5JLUOItckhpnkUtS4yxySWqcRS5JjbPIJalxSyryJBcm+W6Sp5LcMKhQkqT+LbrIk6wA/gz4BeAM4PIkZwwqmCSpP0s5Iz8HeKqqnq6qV4C/AS4ZTCxJUr9SVYv7xuRS4MKqurq7fwXwM1V17axxm4BN3d3Tge8uPu6SrQaeH+Hz96uVnNBOVnMOVis5oZ2sC+VcX1Vr5vvGlcPJ8wNVtRnYPOzn6UeSbVU1OeocvbSSE9rJas7BaiUntJN1KTmXsrQyBZwy4/7abp8kaRktpcj/BTgtyalJ3gRcBmwZTCxJUr8WvbRSVQeTXAv8A7ACuLWqHh9YsuEYiyWePrSSE9rJas7BaiUntJN10TkX/cdOSdJ48JWdktQ4i1ySGnfUFnmSFUm+nWTrHMeuSnIgyfbudvWIMu5K8liXYdscx5Pkj7u3QHg0ydljmvP8JC/OmM/fH0XOLssJSe5K8p0kO5O8Z9bxcZnTXjlHPqdJTp/x/NuTvJTkulljxmU++8k68jntcvx2kseT7EhyZ5I3zzr+o0m+3M3pQ0k29HzQqjoqb8DvAHcAW+c4dhXwp2OQcReweoHjFwFfBwKcCzw0pjnPn2ueR5T1NuDqbvtNwAljOqe9co7NnHZ5VgD7mH5hytjNZ59ZRz6nwMnA94C3dPe/Alw1a8xvAF/oti8DvtzrcY/KM/Ika4FfBG4edZYlugT4y5r2z8AJSSZGHWpcJXk78D7gFoCqeqWq/mPWsJHPaZ85x80FwL9V1e5Z+0c+n3OYL+u4WAm8JclK4K3Av886fgnTP+gB7gIuSJKFHvCoLHLgj4DfBV5bYMwvdb8K3pXklAXGDVMB9yV5uHsrg9lOBvbMuP9st2+59coJ8J4k/5rk60l+cjnDzXAqcAD4i25Z7eYkx80aMw5z2k9OGI85Pewy4M459o/DfM42X1YY8ZxW1RTwGeAZYC/wYlXdN2vY63NaVQeBF4EfW+hxj7oiT7IR2F9VDy8w7O+BDVX1U8D9/OCn33J7b1WdzfQ7SH4syftGlKOXXjkfYfrX2HcDfwL83TLnO2wlcDZwU1WdBfwXMI5vr9xPznGZUzL9gr+Lgb8dVYZ+9cg68jlNciLTZ9ynAj8BHJfkV5b6uEddkQPnARcn2cX0OzL+fJK/njmgqr5fVf/X3b0Z+Onljfh6jqnu637gHqbfUXKmsXgbhF45q+qlqvrPbvteYFWS1cudk+mzwWer6qHu/l1MF+ZM4zCnPXOO0ZzC9A/wR6rquTmOjcN8zjRv1jGZ0/cD36uqA1X1KnA38LOzxrw+p93yy9uB7y/0oEddkVfV71XV2qrawPSvWP9YVW/4iTdrDe9iYOcyRjyc4bgkxx/eBj4I7Jg1bAvwq92VAecy/WvY3nHLmeSdh9fwkpzD9P+rBf/jDUNV7QP2JDm923UB8MSsYSOf035yjsucdi5n/qWKkc/nLPNmHZM5fQY4N8lbuywX8MP9swW4stu+lOkOW/CVm0N/98NxkeQPgW1VtQX4rSQXAweBF5i+imW5nQTc0/2/WgncUVXfSPJrAFX1BeBepq8KeAr4b+AjY5rzUuDXkxwE/ge4rNd/vCH6TeD27lfsp4GPjOGc9pNzLOa0++H9AeCaGfvGcT77yTryOa2qh5LcxfQyz0Hg28DmWf10C/BXSZ5iup8u6/W4vkRfkhp31C2tSNKxxiKXpMZZ5JLUOItckhpnkUtS4yxySWqcRS5Jjft/pOud6c8up0cAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Pandas를 이용한 시각화\n",
    "df_iris['Sepal.Length'].hist(bins=n_bins, grid=False, edgecolor='black')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Text(0.5, 1.0, 'bins = 9')"
      ]
     },
     "execution_count": 6,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEWCAYAAABv+EDhAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUgUlEQVR4nO3df7RdZX3n8fcHAiqCRUsmgzFpqKWsidSiRKoRqxbboR0KdcoysByLHTXpoK1MqbMoztSusZ3Rqf1hrSJRqHSKNJbCFBxHQQv+GBymAVN+M1IKJgQhqIC2Vgl854+zgze398e5Iefsc3ner7XOuvvs/Zy9v3nWzfnc/ex9npOqQpLUnn36LkCS1A8DQJIaZQBIUqMMAElqlAEgSY0yACSpUQaAntSS3JXkVbNse1mS28ddkzQpDAA1q6o+X1VH9F3HLkl+NslNSb6V5Jokq/uuSU9uBoA0AZIcDlwI/BJwMHA5cFmSJX3WpSc3A0AteFGSW5J8I8kfJ3kqQJJXJNm2q1E3XPRrSW5I8lCSTVPaHpLk40keTPL1JJ9Psjf///xL4PNV9YWq2gm8G1gOvHwvHkPajQGgFryWwRvsc4EfBv7jHG1fAxwPHAY8H3h9t/5MYBuwFFgGnA3MOI9KFyAPzvL4wBzHzrTlAEfO94+T9pQBoBb8UVVtraqvA78NnDpH2z+squ1d28uBo7r1jwCHAj9QVY901w9mDICqen5VHTzL4/RZjvtp4OXdWcn+DAJmf+CAhf9zpeEYAGrB1inLdwPPnqPtV6cs/wNwYLf8O8AdwBVJ7kxy1t4ssKpuA04D/gi4FzgEuIXBWYc0EgaAWrBiyvJKYPtCd1BV36yqM6vqB4ETgV9NctxMbZPc3N3JM9Pjg3Mc4+KqOrKqvh94B7AK+OuF1ioNyzsM1II3J/k4g7/o3w5sWugOkpwA3Ab8LfAQ8Cjw2Extq+p5e1JkkqOBLcCzgPcDl3VnBtJIeAagFnwUuAK4k8Eb+G/twT4OZzBO/y3gi8AHquqqvVbhwHuBB4HbgW8Ab9rL+5d2E78QRpLa5BmAJDXKAJCkRhkAktQoA0CSGrUobgM95JBDatWqVX2XIUmLynXXXfdAVS2dbfuiCIBVq1axefPmvsuQpEUlyd1zbXcISJIaZQBIUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGrUoPgmsJ5/lK1ayfdvW+RuO0L77PYVHH/lOrzUAPPs5K7hn61f6LkMNMgDUi+3btrLu3Gt6rWHThrW917CrDqkPDgFJUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSo0YWAElWJLkqyS1Jbk7y1m79bya5J8mW7vEzo6pBkjS7UX4l5E7gzKq6PslBwHVJruy2/X5VvWeEx5YkzWNkAVBV9wL3dsvfTHIrsHxUx5MkLcxYrgEkWQW8ALi2W/WWJDckOT/JM2d5zfokm5Ns3rFjxzjKlKSmjDwAkhwI/AVwRlU9DJwDPBc4isEZwu/O9Lqq2lhVa6pqzdKlS0ddpiQ1Z6QBkGQ/Bm/+F1bVJQBVdV9VPVpVjwEfAo4ZZQ2SpJmN8i6gAOcBt1bV701Zf+iUZq8GbhpVDZKk2Y3yLqCXAq8DbkyypVt3NnBqkqOAAu4CNoywBknSLEZ5F9AXgMyw6ROjOqYkaXh+EliSGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAIzJ8hUrSdL7Y/mKlX13haQJMcq5gDTF9m1bWXfuNX2XwaYNa/suQdKE8AxAkhplAEhSowwASWqUASBJjTIAJKlRBoAkNcoAkKRGGQCS1CgDQJIaZQBIUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGjWyAEiyIslVSW5JcnOSt3brn5XkyiRf7n4+c1Q1SJJmN8ozgJ3AmVW1Gngx8OYkq4GzgM9U1eHAZ7rnkqQxG1kAVNW9VXV9t/xN4FZgOXAScEHX7ALg50ZVgyRpdmP5Uvgkq4AXANcCy6rq3m7TV4Fls7xmPbAeYOXKlWOoshH7LCFJ31VImgAjD4AkBwJ/AZxRVQ9PffOpqkpSM72uqjYCGwHWrFkzYxvtgcd2su7ca/qugk0b1vZdgtS8kd4FlGQ/Bm/+F1bVJd3q+5Ic2m0/FLh/lDVIkmY2yruAApwH3FpVvzdl02XAad3yacBfjqoGSdLsRjkE9FLgdcCNSbZ0684G3gV8LMkbgLuB14ywBknSLEYWAFX1BWC2q43Hjeq4kqTh+ElgSWqUASBJjTIAJKlRBoAkNcoAkKRGGQCS1CgDQJIaZQBIUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGmUASFKjDABJACxfsZIkvT+Wr1jZd1c0Y5RfCSlpEdm+bSvrzr2m7zLYtGFt3yU0wzMASWqUASBJjTIAJKlRQwVAkpcOs06StHgMewbwviHXSZIWiTnvAkryEmAtsDTJr07Z9Axg31EWJkkarfluA90fOLBrd9CU9Q8DJ4+qKEnS6M0ZAFX1WeCzST5SVXePqSZJ0hgM+0GwpyTZCKya+pqq+olRFCVJGr1hA+DPgQ8CHwYeHV05kqRxGTYAdlbVOQvZcZLzgROA+6vqyG7dbwJvAnZ0zc6uqk8sZL+SpL1j2NtAL09yepJDkzxr12Oe13wEOH6G9b9fVUd1D9/8Jaknw54BnNb9fNuUdQX84GwvqKrPJVm1h3VJkkZsqACoqsP24jHfkuQXgM3AmVX1jZkaJVkPrAdYudLpYSVpbxsqALo37H+iqv5kgcc7B3gng7OHdwK/C/zbWfa9EdgIsGbNmlrgcSRJ8xh2COhFU5afChwHXA8sKACq6r5dy0k+BHx8Ia+XJO09ww4B/fLU50kOBv5soQdLcmhV3ds9fTVw00L3IUnaO/b0G8H+HpjzukCSi4BXAIck2Qa8A3hFkqMYDAHdBWzYw+NLkp6gYa8BXM7gTRsGk8D9C+Bjc72mqk6dYfV5C6pOkjQyw54BvGfK8k7g7qraNoJ6JEljMuw1gM8mWcb3LgZ/eXQlSY3ZZwlJ+q5CDRp2COg1wO8AVwMB3pfkbVV18Qhrk9rw2E7WnXtN31WwacPavkvQmA07BPR24EVVdT9AkqXApwEDQJIWqWHnAtpn15t/52sLeK0kaQINewbwySSfAi7qnq8DnMhNkhax+b4T+IeAZVX1tiT/Gji22/RF4MJRFydJGp35zgD+APh1gKq6BLgEIMmPdNt+doS1SZJGaL5x/GVVdeP0ld26VSOpSJI0FvMFwMFzbHvaXqxDkjRm8wXA5iRvmr4yyRuB60ZTkiRpHOa7BnAGcGmS1/K9N/w1wP4MZvOUJC1ScwZAN3//2iSvBI7sVv/PqvqrkVcmSRqpYecCugq4asS1SJLGyE/zSlKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlRBoAkNcoAkKRGjSwAkpyf5P4kN01Z96wkVyb5cvfzmaM6viRpbqM8A/gIcPy0dWcBn6mqw4HPdM8lST0YWQBU1eeAr09bfRJwQbd8AfBzozq+JGlu474GsKyq7u2Wvwosm61hkvVJNifZvGPHjvFUJ0kN6e0icFUVUHNs31hVa6pqzdKlS8dYmSS1YdwBcF+SQwG6n/eP+fiSpM64A+Ay4LRu+TTgL8d8fElSZ5S3gV4EfBE4Ism2JG8A3gX8ZJIvA6/qnkuSerBkVDuuqlNn2XTcqI4pSRqenwSWpEaN7AxgUixfsZLt27b2XYYkTZwnfQBs37aVdede03cZbNqwtu8SJGk3DgFJUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlRBoAkzWD5ipUk6f2xfMXKkf0bl4xsz5K0iG3ftpV1517Tdxls2rB2ZPv2DECSGmUASFKjDABJalQv1wCS3AV8E3gU2FlVa/qoQ5Ja1udF4FdW1QM9Hl+SmuYQkCQ1qq8zgAKuSFLAuVW1cXqDJOuB9QArV47uPlhJE2afJSTpu4om9BUAx1bVPUn+GXBlktuq6nNTG3ShsBFgzZo11UeRknrw2M4n/f33k6KXIaCquqf7eT9wKXBMH3VIUsvGHgBJnp7koF3LwE8BN427DklqXR9DQMuAS7sxviXAR6vqkz3UIUlNG3sAVNWdwI+O+7iSpN15G6gkNcoAkKRGGQCS1CgDQJIaZQBIUqMMAElqlAEgSY0yACSpUQaAJDXKAJCkRhkAktQoA0CSGmUASFKjDABJapQBIEmNMgAkqVEGgCQ1ygCQpEYZAJLUKANAkhplAEhSowwASWqUASBJjTIAJKlRBoAkNcoAkKRGGQCS1CgDQJIa1UsAJDk+ye1J7khyVh81SFLrxh4ASfYF3g/8NLAaODXJ6nHXIUmt6+MM4Bjgjqq6s6q+C/wZcFIPdUhS01JV4z1gcjJwfFW9sXv+OuDHquot09qtB9Z3T48Abh9robs7BHigx+MPa7HUCYunVuvcuxZLnbB4ap2rzh+oqqWzvXDJaOp54qpqI7Cx7zoAkmyuqjV91zGfxVInLJ5arXPvWix1wuKp9YnU2ccQ0D3AiinPn9OtkySNUR8B8NfA4UkOS7I/cApwWQ91SFLTxj4EVFU7k7wF+BSwL3B+Vd087joWaCKGooawWOqExVOrde5di6VOWDy17nGdY78ILEmaDH4SWJIaZQBIUqMMgGmS7JvkS0k+PsO21yfZkWRL93hjTzXeleTGrobNM2xPkj/sptq4IckLJ7TOVyR5aEp//kYfdXa1HJzk4iS3Jbk1yUumbZ+UPp2vzt77NMkRU46/JcnDSc6Y1mZS+nOYWnvv066Of5/k5iQ3JbkoyVOnbX9Kkk1dn16bZNV8+5zYzwH06K3ArcAzZtm+afqH1nryyqqa7cMfPw0c3j1+DDin+9mHueoE+HxVnTC2amb3XuCTVXVyd3faAdO2T0qfzlcn9NynVXU7cBQ8PvXLPcCl05pNRH8OWSv03KdJlgO/Aqyuqm8n+RiDOyg/MqXZG4BvVNUPJTkFeDewbq79egYwRZLnAP8K+HDftTxBJwF/UgP/Bzg4yaF9FzWpknwf8OPAeQBV9d2qenBas977dMg6J81xwN9W1d3T1vfenzOYrdZJsQR4WpIlDIJ/+7TtJwEXdMsXA8clyVw7NAB29wfAfwAem6PNz3enrBcnWTFHu1Eq4Iok13VTZky3HNg65fm2bt24zVcnwEuS/E2S/5XkeeMsborDgB3AH3fDfx9O8vRpbSahT4epEyajT3c5BbhohvWT0J/TzVYr9NynVXUP8B7gK8C9wENVdcW0Zo/3aVXtBB4Cvn+u/RoAnSQnAPdX1XVzNLscWFVVzweu5HtpO27HVtULGZxGvznJj/dUx3zmq/N6BnOV/CjwPuB/jLm+XZYALwTOqaoXAH8PTOI05cPUOSl9SjdEdSLw533VMKx5au29T5M8k8Ff+IcBzwaenuTfPNH9GgDf81LgxCR3MZih9CeS/OnUBlX1tar6Tvf0w8DR4y3x8Tru6X7ez2C88phpTSZiuo356qyqh6vqW93yJ4D9khwy7joZ/PW5raqu7Z5fzOCNdqpJ6NN565ygPoVB8F9fVffNsG0S+nOqWWudkD59FfB3VbWjqh4BLgHWTmvzeJ92w0TfB3xtrp0aAJ2q+vWqek5VrWJwKvhXVbVbwk4bozyRwcXisUry9CQH7VoGfgq4aVqzy4Bf6O60eDGD08V7J63OJP981xhlkmMY/D7O+Qs7ClX1VWBrkiO6VccBt0xr1nufDlPnpPRp51RmH1LpvT+nmbXWCenTrwAvTnJAV8tx/NP3n8uA07rlkxm8h835SV/vAppHkv8MbK6qy4BfSXIisBP4OvD6HkpaBlza/T4uAT5aVZ9M8ksAVfVB4BPAzwB3AP8A/OKE1nky8O+S7AS+DZwy3y/sCP0ycGE3FHAn8IsT2KfD1DkRfdqF/k8CG6asm8T+HKbW3vu0qq5NcjGD4aidwJeAjdPen84D/nuSOxi8P50y336dCkKSGuUQkCQ1ygCQpEYZAJLUKANAkhplAEhSowwALXpJ3t7NknhDBrM17rVJxTKYCXKmmWFXJZn++Yu9KsnZ4zye2mMAaFHLYDrkE4AXdlN0vIrd55hZzM6ev4m05wwALXaHAg/smqKjqh6oqu1Jjk7y2W4iuk/t+hR3kquTvLc7U7ip+2QnSY5J8sVukrVrpnzadkHmOe67k/zfJP8vycu69Qck+ViSW5JcmsE87muSvIvBzI9bklzY7X7fJB/qznauSPK0J9h3apwBoMXuCmBF96b6gSQvT7Ifg0m7Tq6qo4Hzgd+e8poDquoo4PRuG8BtwMu6SdZ+A/gvCy1kiOMuqapjgDOAd3TrTmcwh/tq4D/RzS9VVWcB366qo6rqtV3bw4H3V9XzgAeBn19ojdJUTgWhRa2qvpXkaOBlwCuBTcBvAUcCV3ZTUezLYArdXS7qXvu5JM9IcjBwEHBBksMZTGO93x6Uc8Q8x72k+3kdsKpbPpbBl7xQVTcluWGO/f9dVW2ZYR/SHjEAtOhV1aPA1cDVSW4E3gzcXFUvme0lMzx/J3BVVb06g6/Su3oPSsk8x901k+yj7Nn/ve9MWX4UcAhIT4hDQFrUMvhO18OnrDqKwSyJS7sLxCTZL7t/ice6bv2xDGahfIjB1Lm7piN+/R6Wc/s8x53J/wZe07VfDfzIlG2PdMNK0kgYAFrsDmQwdHNLN3yymsEY/snAu5P8DbCF3edO/8ckXwI+yOB7VAH+G/Bfu/Uz/nXeXZyd+nWhRyTZtuvB4As75jruTD7AIDRuYTB0dTODb3IC2AjcMOUisLRXORuompLkauDXqmpz37XA419Evl9V/WOS5wKfBo6oqu/2XJoa4DUAqV8HAFd1Qz0BTvfNX+PiGYAkNcprAJLUKANAkhplAEhSowwASWqUASBJjfr/6lQTy1MZ/EQAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Seaborn을 이용한 시각화\n",
    "sns.histplot(x=df_iris['Sepal.Length'],bins=n_bins)\n",
    "plt.title(f'bins = {n_bins}')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 이산확률분포\n",
    "\n",
    "확률변수가 취할 수 있는 값이 이산적인 확률변수\n",
    "\n",
    "**확률질량함수(Probability mass function)**\n",
    "\n",
    "확률변수 X 가 취할 수 있는 값에 대한 집합 $X = {x_1, x_2, x_3, ...}$ 일때, 확률변수 X가 $x_k$를 취할 확률\n",
    "\n",
    "$$f(x) = P(X = x_k) = p_k \\quad (k = 1, 2, 3, ...)$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**누적분포함수(Cumulative distribution function)**\n",
    "\n",
    "확률변수 X가 x이하가 될 때의 확률\n",
    "\n",
    "$$F(x) = P(X \\leq x_k) = \\sum_{x_k \\leq x}f(x_k)$$ \n",
    "\n",
    "**기대값(Expted value)**\n",
    "\n",
    "확률변수의 평균\n",
    "\n",
    "$$E(X) = \\sum_kx_kf(x_k)$$\n",
    "\n",
    "**분산(Variance)**\n",
    "\n",
    "$$V(X) = \\sum_k(x_k - \\mu)^2f(x_k)$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 이산균등분포 (Discrete Uniform Distribution)\n",
    "\n",
    "사상이 일어나는 확률이 같은 분포, 확률변수가 x = {1, ..., n} 1,2,3, .. 값은 이산 값을 취할때,\n",
    "\n",
    "**확률질량함수**\n",
    "\n",
    "베르누이 분포에서 1이 나오는 확률을 p 라고 할때, \n",
    "\n",
    "$$f(x) = \\frac{1}{n} \\quad (x \\in {1, 2, ..., n})$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = \\frac{n+1}{2} \\quad V(X) = \\frac{n^2 - 1}{12}$$\n",
    "\n",
    "![](https://www.researchgate.net/profile/Lakshmi-Padmaja-Dhyaram/publication/319013233/figure/fig3/AS:525690496917504@1502345789065/Uniform-Distribution-Types.png)\n",
    "\n",
    "https://www.researchgate.net/figure/Uniform-Distribution-Types_fig3_319013233\n",
    "\n",
    "**Further Reading**\n",
    "* [이산균등분포](https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%82%B0%EA%B7%A0%EB%93%B1%EB%B6%84%ED%8F%AC)\n",
    "* [Discrete uniform distribution](https://en.wikipedia.org/wiki/Discrete_uniform_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution '), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 7,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEGCAYAAACkQqisAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAVb0lEQVR4nO3dfbRddX3n8fdH4gM4KiCRaoAGLZVBi0rDQ5djfaAiamuYGXRpbY0OmlktttVpp4LTVRwtXdgHqdSqZYThoSgipZJRHCeiaOsaHoKggg+TLBVJBIkGxSoVg9/54/xuOYR7w8kv95yTm/t+rXXX3fu3f3vv79kk+bAfzm+nqpAkqcdDpl2AJGnhMkQkSd0MEUlSN0NEktTNEJEkdVsy7QImbb/99qvly5dPuwxJWjCuv/7671TV0tmWLboQWb58OevWrZt2GZK0YCS5Za5lXs6SJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktRtbCGS5NwkdyS5aaht3yRrk6xvv/dp7UlyVpINSb6Q5IihdVa1/uuTrBpq/8UkX2zrnJUk4/oskqTZjfMb6+cB7wIuGGo7Bbiyqs5IckqbfxPwQuCQ9nM08B7g6CT7AqcBK4ACrk+ypqrubH1eB1wDXAEcD3xsjJ+HM274zqztpzxjv3HuVtICtFj+vRhbiFTVZ5Is36Z5JfCcNn0+cBWDEFkJXFCD1yxenWTvJI9vfddW1RaAJGuB45NcBTy6qq5u7RcAJzDmENH0LZa/mNJCMemxs/avqtva9O3A/m16GXDrUL+NrW177RtnaZ9VktXAaoCDDjpoJ8rXDP8xnz7/G2hXMLUBGKuqkkzkBe9VdTZwNsCKFSt8qbw0JtMKNgP1PpM+FpN+Ouvb7TIV7fcdrX0TcOBQvwNa2/baD5ilXZI0QZM+E1kDrALOaL8vH2p/fZKLGdxY/35V3Zbk48CfzjzFBRwHnFpVW5LcleQYBjfWXwX89SQ/yCT5f1m7Nv/7aDEbW4gk+QCDG+P7JdnI4CmrM4BLkpwE3AK8rHW/AngRsAH4EfAagBYWbwOua/3eOnOTHfhtBk+A7cnghro31SVpwsb5dNYr5lh07Cx9Czh5ju2cC5w7S/s64Kk7U6Mkaef4jXVJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd2mEiJJ3pjk5iQ3JflAkkckOTjJNUk2JPlgkoe1vg9v8xva8uVD2zm1tX81yQum8VkkaTGbeIgkWQb8LrCiqp4K7AG8HHg7cGZV/RxwJ3BSW+Uk4M7WfmbrR5LD2npPAY4H3p1kj0l+Fkla7KZ1OWsJsGeSJcBewG3A84BL2/LzgRPa9Mo2T1t+bJK09our6sdV9XVgA3DUZMqXJMEUQqSqNgF/AXyTQXh8H7ge+F5VbW3dNgLL2vQy4Na27tbW/7HD7bOscz9JVidZl2Td5s2b5/cDSdIiNo3LWfswOIs4GHgC8EgGl6PGpqrOrqoVVbVi6dKl49yVJC0q07ic9SvA16tqc1X9BLgMeCawd7u8BXAAsKlNbwIOBGjLHwN8d7h9lnUkSRMwjRD5JnBMkr3avY1jgS8BnwJObH1WAZe36TVtnrb8k1VVrf3l7emtg4FDgGsn9BkkSQxucE9UVV2T5FLgc8BW4AbgbOCjwMVJ/qS1ndNWOQe4MMkGYAuDJ7KoqpuTXMIggLYCJ1fVvRP9MJK0yE08RACq6jTgtG2av8YsT1dV1b8AL51jO6cDp897gZKkkfiNdUlSN0NEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktRtpBBJ8gvjLkSStPCMeiby7iTXJvntJI8Za0WSpAVjpBCpqmcBrwQOBK5P8v4kzx9rZZKkXd7I90Sqaj3wR8CbgGcDZyX5SpL/MK7iJEm7tlHviRye5Ezgy8DzgF+rqn/bps8cY32SpF3YkhH7/TXwPuDNVXX3TGNVfSvJH42lMknSLm/Uy1kvBt4/EyBJHpJkL4CqunBHd5pk7ySXtsthX07yS0n2TbI2yfr2e5/WN0nOSrIhyReSHDG0nVWt//okq3a0DknSzhk1RD4B7Dk0v1dr6/VO4H9X1aHA0xhcJjsFuLKqDgGubPMALwQOaT+rgfcAJNkXOA04GjgKOG0meCRJkzFqiDyiqv55ZqZN79Wzw/aI8C8D57Rt3VNV3wNWAue3bucDJ7TplcAFNXA1sHeSxwMvANZW1ZaquhNYCxzfU5Mkqc+oIfLDbS4j/SJw93b6b8/BwGbgfya5Icn7kjwS2L+qbmt9bgf2b9PLgFuH1t/Y2uZqf4Akq5OsS7Ju8+bNnWVLkrY1aoi8AfhQkn9M8k/AB4HXd+5zCXAE8J6qegbwQ+67dAVAVRVQndt/gKo6u6pWVNWKpUuXztdmJWnRG+nprKq6LsmhwJNb01er6ied+9wIbKyqa9r8pQxC5NtJHl9Vt7XLVXe05ZsYfMlxxgGtbRPwnG3ar+qsSZLUYUcGYDwSOJzBWcQrkryqZ4dVdTtwa5KZQDoW+BKwBph5wmoVcHmbXgO8qj2ldQzw/XbZ6+PAcUn2aTfUj2ttkqQJGelMJMmFwJOAG4F7W3MBF3Tu93eAi5I8DPga8BoGgXZJkpOAW4CXtb5XAC8CNgA/an2pqi1J3gZc1/q9taq2dNYjSeow6pcNVwCHtXsVO62qbmzb3Naxs/Qt4OQ5tnMucO581CRJ2nGjXs66CfiZcRYiSVp4Rj0T2Q/4UpJrgR/PNFbVS8ZSlSRpQRg1RN4yziIkSQvTqI/4fjrJzwKHVNUn2rhZe4y3NEnSrm7UoeBfx+D7HH/bmpYBHx5TTZKkBWLUG+snA88E7oJ/fUHV48ZVlCRpYRg1RH5cVffMzCRZwjwOSyJJWphGDZFPJ3kzsGd7t/qHgP81vrIkSQvBqCFyCoORd78I/GcG3yL3jYaStMiN+nTWT4H/0X4kSQJGHzvr68xyD6SqnjjvFUmSFowdGTtrxiOAlwL7zn85kqSFZKR7IlX13aGfTVX1V8CLx1uaJGlXN+rlrCOGZh/C4Mxk1LMYSdJuatQg+Muh6a3AN7jvfR+SpEVq1KeznjvuQiRJC8+ol7P+y/aWV9U75qccSdJCsiNPZx3J4H3nAL8GXAusH0dRkqSFYdQQOQA4oqp+AJDkLcBHq+o3xlWYJGnXN+qwJ/sD9wzN39PaJEmL2KhnIhcA1yb5hzZ/AnD+WCqSJC0Yoz6ddXqSjwHPak2vqaobxleWJGkhGPVyFsBewF1V9U5gY5KDx1STJGmBGPX1uKcBbwJObU0PBf5uXEVJkhaGUc9E/j3wEuCHAFX1LeBR4ypKkrQwjBoi91RV0YaDT/LI8ZUkSVooRg2RS5L8LbB3ktcBn8AXVEnSovegT2clCfBB4FDgLuDJwB9X1dox1yZJ2sU9aIhUVSW5oqp+ATA4JEn/atTLWZ9LcuRYK5EkLTijfmP9aOA3knyDwRNaYXCScvi4CpMk7fq2GyJJDqqqbwIvmFA9kqQF5MEuZ30YoKpuAd5RVbcM/+zMjpPskeSGJB9p8wcnuSbJhiQfTPKw1v7wNr+hLV8+tI1TW/tXkxh0kjRhDxYiGZp+4jzv+/eALw/Nvx04s6p+DrgTOKm1nwTc2drPbP1IchjwcuApwPHAu5PsMc81SpK248FCpOaY3ilJDgBeDLyvzQd4HnBp63I+g5GCAVZy34jBlwLHtv4rgYur6sdV9XVgA3DUfNUoSXpwD3Zj/WlJ7mJwRrJnm4b7bqw/unO/fwX8IfcNnfJY4HtVtbXNbwSWtellwK0Mdrg1yfdb/2XA1UPbHF7nfpKsBlYDHHTQQZ0lS5K2td0zkarao6oeXVWPqqolbXpmvitAkvwqcEdVXd9VcYeqOruqVlTViqVLl05qt5K02xv1Ed/59EzgJUleBDwCeDTwTgZDqixpZyMHAJta/03AgQyGn18CPAb47lD7jOF1JEkTsCPvE5kXVXVqVR1QVcsZ3Bj/ZFW9EvgUcGLrtgq4vE2vafO05Z9sg0GuAV7ent46GDgEuHZCH0OSxHTORObyJuDiJH8C3ACc09rPAS5MsgHYwiB4qKqbk1wCfAnYCpxcVfdOvmxJWrymGiJVdRVwVZv+GrM8XVVV/wK8dI71TwdOH1+FkqTtmfjlLEnS7sMQkSR1M0QkSd0MEUlSN0NEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRJHUzRCRJ3QwRSVI3Q0SS1M0QkSR1M0QkSd0MEUlSN0NEktTNEJEkdTNEJEndDBFJUreJh0iSA5N8KsmXktyc5Pda+75J1iZZ337v09qT5KwkG5J8IckRQ9ta1fqvT7Jq0p9Fkha7aZyJbAV+v6oOA44BTk5yGHAKcGVVHQJc2eYBXggc0n5WA++BQegApwFHA0cBp80EjyRpMiYeIlV1W1V9rk3/APgysAxYCZzfup0PnNCmVwIX1MDVwN5JHg+8AFhbVVuq6k5gLXD85D6JJGmq90SSLAeeAVwD7F9Vt7VFtwP7t+llwK1Dq21sbXO1z7af1UnWJVm3efPm+fsAkrTITS1Ekvwb4O+BN1TVXcPLqqqAmq99VdXZVbWiqlYsXbp0vjYrSYveVEIkyUMZBMhFVXVZa/52u0xF+31Ha98EHDi0+gGtba52SdKETOPprADnAF+uqncMLVoDzDxhtQq4fKj9Ve0prWOA77fLXh8HjkuyT7uhflxrkyRNyJIp7POZwG8CX0xyY2t7M3AGcEmSk4BbgJe1ZVcALwI2AD8CXgNQVVuSvA24rvV7a1VtmcgnkCQBUwiRqvonIHMsPnaW/gWcPMe2zgXOnb/qJEk7wm+sS5K6GSKSpG6GiCSpmyEiSepmiEiSuhkikqRuhogkqZshIknqZohIkroZIpKkboaIJKmbISJJ6maISJK6GSKSpG6GiCSpmyEiSepmiEiSuhkikqRuhogkqZshIknqZohIkroZIpKkboaIJKmbISJJ6maISJK6GSKSpG6GiCSpmyEiSepmiEiSuhkikqRuhogkqZshIknqtuBDJMnxSb6aZEOSU6ZdjyQtJgs6RJLsAfwN8ELgMOAVSQ6bblWStHgs6BABjgI2VNXXquoe4GJg5ZRrkqRFI1U17Rq6JTkROL6qXtvmfxM4uqpev02/1cDqNvtk4Kudu9wP+E7nursbj8X9eTzuz+Nxn93hWPxsVS2dbcGSSVcyDVV1NnD2zm4nybqqWjEPJS14Hov783jcn8fjPrv7sVjol7M2AQcOzR/Q2iRJE7DQQ+Q64JAkByd5GPByYM2Ua5KkRWNBX86qqq1JXg98HNgDOLeqbh7jLnf6kthuxGNxfx6P+/N43Ge3PhYL+sa6JGm6FvrlLEnSFBkikqRuhsgckpyb5I4kNw217ZtkbZL17fc+06xxUuY4Fn+e5CtJvpDkH5LsPcUSJ2q24zG07PeTVJL9plHbpM11LJL8TvvzcXOSP5tWfZM2x9+Vpye5OsmNSdYlOWqaNc43Q2Ru5wHHb9N2CnBlVR0CXNnmF4PzeOCxWAs8taoOB/4fcOqki5qi83jg8SDJgcBxwDcnXdAUncc2xyLJcxmMHPG0qnoK8BdTqGtazuOBfzb+DPjvVfV04I/b/G7DEJlDVX0G2LJN80rg/DZ9PnDCJGualtmORVX9n6ra2mavZvAdnUVhjj8bAGcCfwgsmqdV5jgWvwWcUVU/bn3umHhhUzLH8Sjg0W36McC3JlrUmBkiO2b/qrqtTd8O7D/NYnYh/wn42LSLmKYkK4FNVfX5adeyC/h54FlJrkny6SRHTrugKXsD8OdJbmVwVrZbnbUbIp1q8Gz0ovk/zrkk+W/AVuCiadcyLUn2At7M4FKFBt8/2xc4BvivwCVJMt2Spuq3gDdW1YHAG4FzplzPvDJEdsy3kzweoP1eNKfps0nyauBXgVfW4v7C0ZOAg4HPJ/kGg0t7n0vyM1Otano2ApfVwLXATxkMQrhYrQIua9MfYjD6+G7DENkxaxj8gaD9vnyKtUxVkuMZXP9/SVX9aNr1TFNVfbGqHldVy6tqOYN/RI+oqtunXNq0fBh4LkCSnwcexsIfxXZnfAt4dpt+HrB+irXMO0NkDkk+APxf4MlJNiY5CTgDeH6S9cCvtPnd3hzH4l3Ao4C17dHF9061yAma43gsSnMci3OBJ7bHXC8GVi2WM9U5jsfrgL9M8nngT7nvtRS7BYc9kSR180xEktTNEJEkdTNEJEndDBFJUjdDRJLUzRCRtpHk3vbY8s1JPt9G5n1IW7YiyVnbWXd5kl/fzvInJLm0Tb86ybt2sLZXJ3nC0Pz7khy2I9uQ5tOCfj2uNCZ3txFXSfI44P0MBtA7rarWAeu2s+5y4NfbOveTZElVfQs4cSdqezVwE20Qv6p67U5sS9ppnolI29FGoF0NvD4Dz0nyEYAkz25nLDcmuSHJoxh8AfVZre2N7cxhTZJPAle2M5Xhd28cmOSq9o6a09p279cnyR8keUuSE4EVwEVt+3u2dVe0fq9I8sUkNyV5+9D6/5zk9HZWdXUSBw7VvDFEpAdRVV8D9gAet82iPwBObmctzwLuZvCOmX+sqqdX1Zmt3xHAiVX1bB7oKOA/AocDL50JhDnquJTBWdAr2/bvnlnWLnG9ncGwGk8HjkxyQlv8SODqqnoa8BkG36CW5oUhIvX7LPCOJL8L7D30fpVtra2q2d4/MrPsuy0QLgP+XWctRwJXVdXmVsdFwC+3ZfcAH2nT1zO45CbNC0NEehBJngjcyzajNlfVGcBrgT2BzyY5dI5N/HA7m9923KFiMLT+8N/NR+xQwQ/0k6Gxq+7Fe6GaR4aItB1JlgLvBd617SCCSZ7URvB9O3AdcCjwAwYDU47q+Un2TbIngzdlfhb4NvC4JI9N8nAGw+3PmGv71wLPTrJfkj2AVwCf3oE6pC7+H4n0QHsmuRF4KIOzgguBd8zS7w3tfeI/BW5m8HbHnwL3thFbzwPufJB9XQv8PYN3kPxde/qLJG9tyzYBXxnqfx7w3iR3A78001hVtyU5BfgUEOCjVbVoX1WgyXEUX0lSNy9nSZK6GSKSpG6GiCSpmyEiSepmiEiSuhkikqRuhogkqdv/BxYiD5QeTg+jAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "rv = sp.stats.randint(low=10, high=20)\n",
    "rvs = rv.rvs(size=100000)\n",
    "ax = sns.distplot(rvs, bins=50, kde=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution ', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 베르누이분포\n",
    "\n",
    "확률변수가 취할 수 있는 값이 0/1 밖에 없는 분포, 가장 기본적인 이산형 확률분포\n",
    "\n",
    "**확률질량함수**\n",
    "\n",
    "베르누이 분포에서 1이 나오는 확률을 p 라고 할때, \n",
    "\n",
    "$$f(x) = p^x(1-p)^{(1-x)} \\quad (x \\in {0, 1})$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = p\\quad V(X) = p(1-p)$$"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "f(0)=0.700, f(1)=0.300\n",
      "F(0)=0.700, F(1)=1.000\n",
      "E(X)=0.300, V(X)=0.210\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution '), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 8,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEGCAYAAACkQqisAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAaIElEQVR4nO3dfbRddX3n8fdHIoJWBCRmaAIN1lSltGK4Qlyt9YERAtMaZlQWVIfIUNIp2Kl9mGnsdE0crWvhmlWpTC02lQyJVRGxSsZCMylqbbsmQijIkzq5opREhEgQqlAp+J0/zu/qIbm5Oex7z7lc836tddbd+7t/e5/fL0+f7OdUFZIkdfG02e6AJGnuMkQkSZ0ZIpKkzgwRSVJnhogkqbN5s92BUTviiCNq8eLFs90NSZozbrzxxm9V1fzJlu13IbJ48WK2bt06292QpDkjyV17W+bhLElSZ4aIJKkzQ0SS1JkhIknqbGghkuSFSW7u+zyU5G1JDk+yOcm29vOw1j5JLkkynuSWJEv7trWytd+WZGVf/YQkt7Z1LkmSYY1HkrSnoYVIVX2lqo6vquOBE4CHgU8Cq4HrqmoJcF2bBzgNWNI+q4BLAZIcDqwBTgJOBNZMBE9rc37fesuHNR5J0p5GdTjrZOCrVXUXsAJY3+rrgTPa9ApgQ/VsAQ5NciRwKrC5qnZV1QPAZmB5W3ZIVW2p3qOIN/RtS5I0AqMKkbOAj7bpBVV1T5v+JrCgTS8E7u5bZ3urTVXfPkldkjQiQw+RJAcCrwM+vvuytgcx9BeaJFmVZGuSrTt37hz210nSfmMUd6yfBvxDVd3b5u9NcmRV3dMOSd3X6juAo/rWW9RqO4BX7Vb/XKsvmqT9HqpqLbAWYGxsrHNoXXTTt7quqiFZ/dIjZrsL0n5tFIezzuaHh7IANgITV1itBK7uq5/TrtJaBjzYDnttAk5Jclg7oX4KsKkteyjJsnZV1jl925IkjcBQ90SSPAt4LfCrfeWLgCuTnAfcBZzZ6tcApwPj9K7kOhegqnYleRdwQ2v3zqra1aYvAC4HDgaubR9J0ogMNUSq6rvAc3er3U/vaq3d2xZw4V62sw5YN0l9K3DcjHRWkvSkece6JKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOhtqiCQ5NMlVSb6c5EtJXp7k8CSbk2xrPw9rbZPkkiTjSW5JsrRvOytb+21JVvbVT0hya1vnkiQZ5ngkSU807D2R9wF/VVUvAl4CfAlYDVxXVUuA69o8wGnAkvZZBVwKkORwYA1wEnAisGYieFqb8/vWWz7k8UiS+gwtRJI8B/gF4DKAqnq0qr4NrADWt2brgTPa9ApgQ/VsAQ5NciRwKrC5qnZV1QPAZmB5W3ZIVW2pqgI29G1LkjQCw9wTOQbYCfyvJDcl+WCSZwELquqe1uabwII2vRC4u2/97a02VX37JPU9JFmVZGuSrTt37pzmsCRJE4YZIvOApcClVfVS4Lv88NAVAG0PoobYh4nvWVtVY1U1Nn/+/GF/nSTtN4YZItuB7VX1hTZ/Fb1QubcdiqL9vK8t3wEc1bf+olabqr5okrokaUSGFiJV9U3g7iQvbKWTgTuAjcDEFVYrgavb9EbgnHaV1jLgwXbYaxNwSpLD2gn1U4BNbdlDSZa1q7LO6duWJGkE5g15+78OfDjJgcCdwLn0guvKJOcBdwFntrbXAKcD48DDrS1VtSvJu4AbWrt3VtWuNn0BcDlwMHBt+0iSRmSoIVJVNwNjkyw6eZK2BVy4l+2sA9ZNUt8KHDe9XkqSuvKOdUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHU21BBJ8vUktya5OcnWVjs8yeYk29rPw1o9SS5JMp7kliRL+7azsrXflmRlX/2Etv3xtm6GOR5J0hONYk/k1VV1fFWNtfnVwHVVtQS4rs0DnAYsaZ9VwKXQCx1gDXAScCKwZiJ4Wpvz+9ZbPvzhSJImzMbhrBXA+ja9Hjijr76herYAhyY5EjgV2FxVu6rqAWAzsLwtO6SqtlRVARv6tiVJGoFhh0gB/yfJjUlWtdqCqrqnTX8TWNCmFwJ39627vdWmqm+fpL6HJKuSbE2ydefOndMZjySpz7whb//nq2pHkucBm5N8uX9hVVWSGnIfqKq1wFqAsbGxoX+fJO0vhronUlU72s/7gE/SO6dxbzsURft5X2u+Aziqb/VFrTZVfdEkdUnSiAwtRJI8K8mzJ6aBU4DbgI3AxBVWK4Gr2/RG4Jx2ldYy4MF22GsTcEqSw9oJ9VOATW3ZQ0mWtauyzunbliRpBIZ5OGsB8Ml21e084CNV9VdJbgCuTHIecBdwZmt/DXA6MA48DJwLUFW7krwLuKG1e2dV7WrTFwCXAwcD17aPJGlEhhYiVXUn8JJJ6vcDJ09SL+DCvWxrHbBukvpW4Lhpd1aS1Il3rEuSOjNEJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM4GCpEkPzPsjkiS5p5B90T+JMn1SS5I8pyh9kiSNGcMFCJV9QrgTfReDnVjko8kee1QeyZJesob+JxIVW0Dfh/4XeCVwCVJvpzk3w2rc5Kkp7ZBz4n8bJKLgS8BrwF+qape3KYvHmL/JElPYYO+lOp/Ah8Efq+qHpkoVtU3kvz+UHomSXrKGzRE/g3wSFU9DpDkacBBVfVwVX1oaL2TJD2lDXpO5K/pvcd8wjNbTZK0Hxs0RA6qqu9MzLTpZw6nS5KkuWLQEPlukqUTM0lOAB6Zor0kaT8waIi8Dfh4kr9N8nfAx4C3DrJikgOS3JTk023+mCRfSDKe5GNJDmz1Z7T58bZ8cd823t7qX0lyal99eauNJ1k94FgkSTNk0JsNbwBeBPwa8B+BF1fVjQN+x2/QuzR4wnuAi6vqBcADwHmtfh7wQKtf3NqR5FjgLOCngeX07p4/IMkBwPuB04BjgbNbW0nSiDyZBzC+DPhZYCm9f7DP2dcKSRbRu7Lrg20+9O4tuao1WQ+c0aZXtHna8pNb+xXAFVX1var6GjAOnNg+41V1Z1U9ClzR2kqSRmSgS3yTfAj4SeBm4PFWLmDDPlb9I+C/AM9u888Fvl1Vj7X57cDCNr0QuBugqh5L8mBrvxDY0rfN/nXu3q1+0l76vwpYBXD00Ufvo8uSpEENep/IGHBsVdWgG07yi8B9VXVjkld16NuMqaq1wFqAsbGxgccgSZraoCFyG/CvgHuexLZ/DnhdktOBg4BDgPcBhyaZ1/ZGFgE7Wvsd9B7wuD3JPOA5wP199Qn96+ytLkkagUHPiRwB3JFkU5KNE5+pVqiqt1fVoqpaTO/E+Geq6k3AZ4E3tGYrgavb9MY2T1v+mbbnsxE4q129dQywBLgeuAFY0q72OrB9x5R9kiTNrEH3RN4xg9/5u8AVSf4AuAm4rNUvAz6UZBzYRS8UqKrbk1wJ3AE8BlzY9/iVtwKbgAOAdVV1+wz2U5K0DwOFSFX9TZKfAJZU1V8neSa9f7gHUlWfAz7Xpu+kd2XV7m3+GXjjXtZ/N/DuSerXANcM2g9J0swa9FHw59O77PZPW2kh8Kkh9UmSNEcMek7kQnonyh+CH7yg6nnD6pQkaW4YNES+127oA6BdPeWlspK0nxs0RP4mye8BB7d3q38c+N/D65YkaS4YNERWAzuBW4FfpXcy2zcaStJ+btCrs74P/Fn7SJIEDP7srK8xyTmQqnr+jPdIkjRnPJlnZ004iN79HIfPfHckSXPJoO8Tub/vs6Oq/ojeI94lSfuxQQ9nLe2bfRq9PZNB92IkST+iBg2CP+ybfgz4OnDmjPdGkjSnDHp11quH3RFJ0twz6OGs35pqeVW9d2a6I0maS57M1Vkv44fv6/gleu/02DaMTkmS5oZBQ2QRsLSq/gkgyTuAv6yqNw+rY5Kkp75BH3uyAHi0b/7RVpMk7ccG3RPZAFyf5JNt/gxg/VB6JEmaMwa9OuvdSa4FXtFK51bVTcPrliRpLhj0cBbAM4GHqup9wPYkxwypT5KkOWLQ1+OuAX4XeHsrPR3482F1SpI0Nwy6J/JvgdcB3wWoqm8Az55qhSQHJbk+yReT3J7kv7f6MUm+kGQ8yceSHNjqz2jz42354r5tvb3Vv5Lk1L768lYbT7L6SY1ckjRtg4bIo1VVtMfBJ3nWAOt8D3hNVb0EOB5YnmQZ8B7g4qp6AfAAcF5rfx7wQKtf3NqR5FjgLOCngeXAnyQ5IMkBwPuB04BjgbNbW0nSiAx6ddaVSf4UODTJ+cB/YB8vqGqh8502+/T2KeA1wC+3+nrgHcClwIo2DXAV8MdJ0upXVNX3gK8lGQdObO3Gq+pOgCRXtLZ3DDgmSUNy0U3fmu0uaDerX3rEULa7zxBp/5B/DHgR8BDwQuC/VdXmAdY9ALgReAG9vYavAt+uqsdak+3Awja9ELgboKoeS/Ig8NxW39K32f517t6tftK++iRJmjn7DJGqqiTXVNXPAPsMjt3WfRw4PsmhwCfpBdHIJVkFrAI4+uijZ6MLkvQjadBzIv+Q5GVdv6Sqvg18Fng5vUNiE+G1CNjRpncARwG05c8B7u+v77bO3uqTff/aqhqrqrH58+d3HYYkaTeDhshJwJYkX01yS5Jbk9wy1QpJ5rc9EJIcDLwW+BK9MHlDa7YSuLpNb2zztOWfaedVNgJntau3jgGW0Hv44w3Akna114H0Tr5PPCBSkjQCUx7OSnJ0Vf0jcOpU7fbiSGB9Oy/yNODKqvp0kjuAK5L8AXATcFlrfxnwoXbifBe9UKCqbk9yJb0T5o8BF7bDZCR5K7AJOABYV1W3d+inJKmjfZ0T+RS9p/feleQTVfX6QTdcVbcAL52kfic/vLqqv/7PwBv3sq13A++epH4NcM2gfZIkzax9Hc5K3/Tzh9kRSdLcs68Qqb1MS5K0z8NZL0nyEL09koPbNG2+quqQofZOkvSUNmWIVNUBo+qIJGnueTKPgpck6QkMEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHVmiEiSOjNEJEmdGSKSpM6GFiJJjkry2SR3JLk9yW+0+uFJNifZ1n4e1upJckmS8SS3JFnat62Vrf22JCv76ickubWtc0mSDGs8kqQ9DXNP5DHgt6vqWGAZcGGSY4HVwHVVtQS4rs0DnAYsaZ9VwKXQCx1gDXAScCKwZiJ4Wpvz+9ZbPsTxSJJ2M7QQqap7quof2vQ/AV8CFgIrgPWt2XrgjDa9AthQPVuAQ5McCZwKbK6qXVX1ALAZWN6WHVJVW6qqgA1925IkjcBIzokkWQy8FPgCsKCq7mmLvgksaNMLgbv7VtvealPVt09Sn+z7VyXZmmTrzp07pzcYSdIPDD1EkvwY8AngbVX1UP+ytgdRw+5DVa2tqrGqGps/f/6wv06S9htDDZEkT6cXIB+uqr9o5XvboSjaz/tafQdwVN/qi1ptqvqiSeqSpBEZ5tVZAS4DvlRV7+1btBGYuMJqJXB1X/2cdpXWMuDBdthrE3BKksPaCfVTgE1t2UNJlrXvOqdvW5KkEZg3xG3/HPDvgVuT3NxqvwdcBFyZ5DzgLuDMtuwa4HRgHHgYOBegqnYleRdwQ2v3zqra1aYvAC4HDgaubR9J0ogMLUSq6u+Avd23cfIk7Qu4cC/bWgesm6S+FThuGt2UJE2Dd6xLkjozRCRJnRkikqTODBFJUmeGiCSpM0NEktSZISJJ6swQkSR1ZohIkjozRCRJnRkikqTODBFJUmeGiCSpM0NEktSZISJJ6swQkSR1ZohIkjozRCRJnRkikqTODBFJUmeGiCSps6GFSJJ1Se5Lcltf7fAkm5Nsaz8Pa/UkuSTJeJJbkiztW2dla78tycq++glJbm3rXJIkwxqLJGlyw9wTuRxYvlttNXBdVS0BrmvzAKcBS9pnFXAp9EIHWAOcBJwIrJkIntbm/L71dv8uSdKQDS1EqurzwK7dyiuA9W16PXBGX31D9WwBDk1yJHAqsLmqdlXVA8BmYHlbdkhVbamqAjb0bUuSNCKjPieyoKruadPfBBa06YXA3X3ttrfaVPXtk9QnlWRVkq1Jtu7cuXN6I5Ak/cCsnVhvexA1ou9aW1VjVTU2f/78UXylJO0XRh0i97ZDUbSf97X6DuCovnaLWm2q+qJJ6pKkERp1iGwEJq6wWglc3Vc/p12ltQx4sB322gSckuSwdkL9FGBTW/ZQkmXtqqxz+rYlSRqRecPacJKPAq8Cjkiynd5VVhcBVyY5D7gLOLM1vwY4HRgHHgbOBaiqXUneBdzQ2r2zqiZO1l9A7wqwg4Fr20eSNEJDC5GqOnsvi06epG0BF+5lO+uAdZPUtwLHTaePkqTp8Y51SVJnhogkqTNDRJLUmSEiSerMEJEkdWaISJI6M0QkSZ0ZIpKkzgwRSVJnhogkqTNDRJLUmSEiSerMEJEkdWaISJI6M0QkSZ0ZIpKkzgwRSVJnhogkqTNDRJLUmSEiSerMEJEkdTbnQyTJ8iRfSTKeZPVs90eS9idzOkSSHAC8HzgNOBY4O8mxs9srSdp/zOkQAU4Exqvqzqp6FLgCWDHLfZKk/ca82e7ANC0E7u6b3w6ctHujJKuAVW32O0m+0vH7jgC+1XHdueopPea3D2ezT+kxD8H+Nl7YD8f89umN+Sf2tmCuh8hAqmotsHa620mytarGZqBLc4Zj/tG3v40XHPNMmuuHs3YAR/XNL2o1SdIIzPUQuQFYkuSYJAcCZwEbZ7lPkrTfmNOHs6rqsSRvBTYBBwDrqur2IX7ltA+JzUGO+Uff/jZecMwzJlU1jO1KkvYDc/1wliRpFhkikqTODJFJ7OtRKkmekeRjbfkXkiyehW7OmAHG+1tJ7khyS5Lrkuz1mvG5YtDH5SR5fZJKMucvBx1kzEnObL/Xtyf5yKj7ONMG+LN9dJLPJrmp/fk+fTb6OVOSrEtyX5Lb9rI8SS5pvx63JFk67S+tKj99H3on6L8KPB84EPgicOxubS4APtCmzwI+Ntv9HvJ4Xw08s03/2lwe76Bjbu2eDXwe2AKMzXa/R/D7vAS4CTiszT9vtvs9gjGvBX6tTR8LfH22+z3NMf8CsBS4bS/LTweuBQIsA74w3e90T2RPgzxKZQWwvk1fBZycJCPs40za53ir6rNV9XCb3ULvfpy5bNDH5bwLeA/wz6Ps3JAMMubzgfdX1QMAVXXfiPs40wYZcwGHtOnnAN8YYf9mXFV9Htg1RZMVwIbq2QIcmuTI6XynIbKnyR6lsnBvbarqMeBB4Lkj6d3MG2S8/c6j9z+ZuWyfY267+UdV1V+OsmNDNMjv808BP5Xk75NsSbJ8ZL0bjkHG/A7gzUm2A9cAvz6ars2aJ/v3fZ/m9H0iGq0kbwbGgFfOdl+GKcnTgPcCb5nlrozaPHqHtF5Fb2/z80l+pqq+PZudGrKzgcur6g+TvBz4UJLjqur7s92xucI9kT0N8iiVH7RJMo/ebvD9I+ndzBvo0TFJ/jXwX4HXVdX3RtS3YdnXmJ8NHAd8LsnX6R073jjHT64P8vu8HdhYVf9SVV8D/h+9UJmrBhnzecCVAFX1f4GD6D2o8EfVjD8qyhDZ0yCPUtkIrGzTbwA+U+2s1Ry0z/EmeSnwp/QCZK4fJ4d9jLmqHqyqI6pqcVUtpnce6HVVtXV2ujsjBvlz/Sl6eyEkOYLe4a07R9jHmTbImP8ROBkgyYvphcjOkfZytDYC57SrtJYBD1bVPdPZoIezdlN7eZRKkncCW6tqI3AZvd3ecXonsc6avR5Pz4Dj/R/AjwEfb9cP/GNVvW7WOj1NA475R8qAY94EnJLkDuBx4D9X1Vzdwx50zL8N/FmS36R3kv0tc/g/hCT5KL3/CBzRzvOsAZ4OUFUfoHfe53RgHHgYOHfa3zmHf70kSbPMw1mSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRdpPk8SQ3tyfZfjHJb7e72EkyluSSKdZdnOSXp1j+40muatNvSfLHT7Jvb0ny433zH0xy7JPZhjSTvE9E2tMjVXU8QJLnAR+h95C+Ne2Gw6luOlwM/HJb5wmSzKuqb9C7QbWrtwC30R4UWFW/Mo1tSdPmnog0hXaH/irgre0u31cl+TRAkle2PZab2/song1cBLyi1X6z7TlsTPIZ4Lq2p9L/roejknwuybYka9p2n9Amye8keUeSN9B7dtmH2/YPbuuOtXZnJ7k1yW1J3tO3/neSvLvtVW1JsmDYv27afxgi0j5U1Z307nh+3m6Lfge4sO21vAJ4BFgN/G1VHV9VF7d2S4E3VNVkD648EXg98LPAG6d6PldVXUVvL+hNbfuPTCxrh7jeA7wGOB54WZIz2uJnAVuq6iX03o9y/oBDl/bJEJG6+3vgvUn+E3Boey3AZDZX1d7e8bC5qu5vgfAXwM937MvLgM9V1c7Wjw/Te0ERwKPAp9v0jfQOuUkzwhCR9iHJ8+k9S+oJD5+sqouAXwEOBv4+yYv2sonvTrH53Z87VMBjPPHv5kFPqsN7+pe+50E9judCNYMMEWkKSeYDHwD+ePcH8yX5yaq6tareQ++JsS8C/oneo+QH9dokhyc5GDiD3t7NvcDzkjw3yTOAX+xrv7ftXw+8MskRSQ6g956Mv3kS/ZA68X8k0p4OTnIzvaefPgZ8iN5Lqnb3tiSvBr4P3E7vjY/fBx5P8kXgcuCBfXzX9cAn6L3X4c8nHjffnjR7Pb13PXy5r/3lwAeSPAK8fKJYVfckWQ18lt77s/+yqq4efMhSNz7FV5LUmYezJEmdGSKSpM4MEUlSZ4aIJKkzQ0SS1JkhIknqzBCRJHX2/wE91z/AOytJ4QAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "p = 0.3\n",
    "rv = sp.stats.bernoulli(p)\n",
    "print(f\"f(0)={rv.pmf(0):.3f}, f(1)={rv.pmf(1):.3f}\")\n",
    "print(f\"F(0)={rv.cdf(0):.3f}, F(1)={rv.cdf(1):.3f}\")\n",
    "print(f\"E(X)={rv.mean():.3f}, V(X)={rv.var():.3f}\")\n",
    "\n",
    "rvs = rv.rvs(size=100000)\n",
    "ax = sns.distplot(rvs, bins=3, kde=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution ', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 이항분포 (Binomial Distribution)\n",
    "\n",
    "성공확률이 p인 베르누이 시행을 n번 했을 때의 성공 횟수가 따르는 분포\n",
    "\n",
    "**확률질량함수**\n",
    "\n",
    "연속된 n번의 독립적 시행에서 각 시행이 성공 확률 p를 가질 때, \n",
    "\n",
    "$$f(x) = nCxp^x(1-p)^{(n-x)} \\quad (x \\in {0, 1, 2, ... n})$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = np\\quad V(X) = np(1-p)$$\n",
    "\n",
    "![](https://upload.wikimedia.org/wikipedia/commons/thumb/7/75/Binomial_distribution_pmf.svg/300px-Binomial_distribution_pmf.svg.png)\n",
    "\n",
    "https://en.wikipedia.org/wiki/Binomial_distribution\n",
    "\n",
    "**Further Reading**\n",
    "* [이항 분포](https://ko.wikipedia.org/wiki/%EC%9D%B4%ED%95%AD_%EB%B6%84%ED%8F%AC)\n",
    "* [Binomial distribution](https://en.wikipedia.org/wiki/Binomial_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "f(1)=0.010, f(8)=0.044\n",
      "F(1)=0.011, F(8)=0.989\n",
      "E(X)=5.000, V(X)=2.500\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 9,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAEHCAYAAABfkmooAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUnUlEQVR4nO3df7DddX3n8edLggpoC2xCFpPYoJOVpbsV2AvSUleUiqCtYGtZaKuRQdOZhVW6utvIdBbGjjNxpkJla2kRs4KiLEWsWZsWI7W66wxCgJSfOmQRJCGQIK6gMiL0vX+c7y3HcG8+55J7zrnJfT5mzpzv9/P99f7OTe7rfn99vqkqJEnalReMuwBJ0txnWEiSmgwLSVKTYSFJajIsJElNhoUkqWnBsFacZBlwJbAYKOCyqvpYkguB9wA7ulnPr6r13TIfBM4GngHeW1XXd+0nAx8D9gEur6o1u9r2woULa/ny5bO+T5K0N7vlllserapFU00bWlgATwPvr6pbk7wUuCXJhm7axVX1J/0zJzkCOAP4ReBlwFeS/Ktu8seBNwJbgJuTrKuqu6fb8PLly9m4ceMs744k7d2SPDDdtKGFRVVtA7Z1w08kuQdYsotFTgWurqqfAN9Jshk4tpu2uaruA0hydTfvtGEhSZpdI7lmkWQ5cBTwza7p3CS3J1mb5KCubQnwYN9iW7q26dp33saqJBuTbNyxY8fOkyVJu2HoYZHkJcDngfOq6nHgUuCVwJH0jjw+OhvbqarLqmqiqiYWLZrylJsk6Xka5jULkuxLLyiuqqrrAKrqkb7pnwC+1I1uBZb1Lb60a2MX7ZKkERjakUWSAJ8E7qmqi/raD+2b7W3And3wOuCMJC9KchiwArgJuBlYkeSwJC+kdxF83bDqliQ91zCPLI4H3gHckWRT13Y+cGaSI+ndTns/8PsAVXVXkmvoXbh+Gjinqp4BSHIucD29W2fXVtVdQ6xbkrST7I1dlE9MTJS3zkrSzCS5paompprmE9ySpCbDQpLUNNS7oSQ915rbHp2yffVRC0dciTQ4jywkSU2GhSSpybCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWoyLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUtOCcRcgjcOa2x6ddtrqoxaOsBJpz+CRhSSpybCQJDUZFpKkJsNCktTkBW5pnpjuor4X9DUIjywkSU2GhSSpaWhhkWRZkq8muTvJXUne17UfnGRDknu774O69iS5JMnmJLcnObpvXSu7+e9NsnJYNUuSpjbMI4ungfdX1RHAccA5SY4AVgM3VNUK4IZuHOAUYEX3WQVcCr1wAS4AXgMcC1wwGTCSpNEYWlhU1baqurUbfgK4B1gCnApc0c12BXBaN3wqcGX13AgcmORQ4E3Ahqp6rKq+D2wATh5W3ZKk5xrJNYsky4GjgG8Ci6tqWzfpYWBxN7wEeLBvsS1d23TtO29jVZKNSTbu2LFjdndAkua5oYdFkpcAnwfOq6rH+6dVVQE1G9upqsuqaqKqJhYtWjQbq5QkdYYaFkn2pRcUV1XVdV3zI93pJbrv7V37VmBZ3+JLu7bp2iVJIzLMu6ECfBK4p6ou6pu0Dpi8o2kl8MW+9nd2d0UdB/ygO111PXBSkoO6C9sndW2SpBEZ5hPcxwPvAO5IsqlrOx9YA1yT5GzgAeD0btp64M3AZuDHwFkAVfVYkj8Gbu7m+1BVPTbEuiVJOxlaWFTV/wEyzeQTp5i/gHOmWddaYO3sVSdJmgmf4JYkNRkWkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSpybCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWoyLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSpybCQJDUZFpKkpoHCIsm/nemKk6xNsj3JnX1tFybZmmRT93lz37QPJtmc5NtJ3tTXfnLXtjnJ6pnWIUnafYMeWfx5kpuS/MckPz/gMp8CTp6i/eKqOrL7rAdIcgRwBvCL3TJ/nmSfJPsAHwdOAY4AzuzmlSSN0EBhUVWvBX4XWAbckuSzSd7YWObrwGMD1nEqcHVV/aSqvgNsBo7tPpur6r6qegq4uptXkjRCA1+zqKp7gT8C/hB4HXBJkm8l+c0ZbvPcJLd3p6kO6tqWAA/2zbOla5uu/TmSrEqyMcnGHTt2zLAkSdKuDHrN4peSXAzcA7wB+I2q+tfd8MUz2N6lwCuBI4FtwEdnVO0uVNVlVTVRVROLFi2ardVKkoAFA87334HLgfOr6snJxqp6KMkfDbqxqnpkcjjJJ4AvdaNb6Z3imrS0a2MX7ZKkERn0NNRbgM9OBkWSFyTZH6CqPj3oxpIc2jf6NmDyTql1wBlJXpTkMGAFcBNwM7AiyWFJXkjvIvi6QbcnSZodgx5ZfAX4NeCH3fj+wJeBX5lugSSfA04AFibZAlwAnJDkSKCA+4HfB6iqu5JcA9wNPA2cU1XPdOs5F7ge2AdYW1V3Db57kqTZMGhYvLiqJoOCqvrh5JHFdKrqzCmaP7mL+T8MfHiK9vXA+gHrlCQNwaCnoX6U5OjJkST/DnhyF/NLkvYigx5ZnAf8VZKHgAD/EvgPwypKkjS3DBQWVXVzksOBV3VN366qnw6vLEnSXDLokQXAMcDybpmjk1BVVw6lKknSnDJQWCT5NL2H6TYBz3TNBRgWkjQPDHpkMQEcUVU1zGIkSXPToHdD3UnvorYkaR4a9MhiIXB3kpuAn0w2VtVbh1KVJGlOGTQsLhxmEZKkuW3QW2e/luQXgBVV9ZXu6e19hluaJGmuGLSL8vcA1wJ/2TUtAf56SDVJkuaYQS9wnwMcDzwO//wipEOGVZQkaW4ZNCx+0r3WFIAkC+g9ZyFJmgcGDYuvJTkf2K979/ZfAf9reGVJkuaSQcNiNbADuIPeOyjW03sftyRpHhj0bqh/Aj7RfSRJ88ygfUN9hymuUVTVK2a9IknSnDOTvqEmvRj4beDg2S9HkjQXDXTNoqq+1/fZWlV/CrxluKVJkuaKQU9DHd03+gJ6RxozeReGJGkPNugv/I/2DT8N3A+cPuvVSJLmpEHvhnr9sAuRJM1dg56G+s+7ml5VF81OOZKkuWgmd0MdA6zrxn8DuAm4dxhFSZLmlkHDYilwdFU9AZDkQuBvqur3hlWYJGnuGDQsFgNP9Y0/1bVJu2XNbY9O2b76qIUjrkTD5M95zzdoWFwJ3JTkC934acAVQ6lIkjTnDHo31IeT/C3w2q7prKq6bXhlSZLmkkF7nQXYH3i8qj4GbEly2JBqkiTNMYO+VvUC4A+BD3ZN+wKfGVZRkqS5ZdAji7cBbwV+BFBVDwEvHVZRkqS5ZdCweKqqiq6b8iQHDK8kSdJcM2hYXJPkL4EDk7wH+Aq+CEmS5o3m3VBJAvxP4HDgceBVwH+rqg1Drk2SNEc0jyy600/rq2pDVf2XqvrAIEGRZG2S7Unu7Gs7OMmGJPd23wd17UlySZLNSW7v7xI9ycpu/nuTrHye+ylJ2g2Dnoa6NckxM1z3p4CTd2pbDdxQVSuAG7pxgFOAFd1nFXAp9MIFuAB4DXAscMFkwEiSRmfQsHgNcGOS/9v95X9Hktt3tUBVfR14bKfmU3n2ye8r6D0JPtl+ZfXcSO/ayKHAm4ANVfVYVX0f2MBzA0iSNGS7vGaR5OVV9V16v7Rnw+Kq2tYNP8yz/UstAR7sm29L1zZd+1S1rqJ3VMLLX/7yWSpXkgTtI4u/BqiqB4CLquqB/s/ubLj/VtzZUFWXVdVEVU0sWrRotlYrSaIdFukbfsUsbO+R7vQS3ff2rn0rsKxvvqVd23TtkqQRaoVFTTP8fK0DJu9oWgl8sa/9nd1dUccBP+hOV10PnJTkoO7C9kldmyRphFrPWbw6yeP0jjD264bpxquqfm66BZN8DjgBWJhkC727mtbQe8DvbOAB4PRu9vXAm4HNwI+Bs+ht4LEkfwzc3M33oara+aK5JGnIdhkWVbXP811xVZ05zaQTp5i3gHOmWc9aYO3zrUOStPtm0kW5JGmeMiwkSU2GhSSpybCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWoyLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSpybCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNYwmLJPcnuSPJpiQbu7aDk2xIcm/3fVDXniSXJNmc5PYkR4+jZkmaz8Z5ZPH6qjqyqia68dXADVW1ArihGwc4BVjRfVYBl468Ukma5+bSaahTgSu64SuA0/rar6yeG4EDkxw6hvokad4aV1gU8OUktyRZ1bUtrqpt3fDDwOJueAnwYN+yW7q2n5FkVZKNSTbu2LFjWHVL0ry0YEzb/dWq2prkEGBDkm/1T6yqSlIzWWFVXQZcBjAxMTGjZSVJuzaWI4uq2tp9bwe+ABwLPDJ5eqn73t7NvhVY1rf40q5NkjQiIw+LJAckeenkMHAScCewDljZzbYS+GI3vA54Z3dX1HHAD/pOV0mSRmAcp6EWA19IMrn9z1bV3yW5GbgmydnAA8Dp3fzrgTcDm4EfA2eNvmRJmt9GHhZVdR/w6inavwecOEV7AeeMoLR5bc1tj07ZvvqohSOuRNJcNK4L3JI0dP4RNHvm0nMWkqQ5yrCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWoyLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSpybCQJDUZFpKkpgXjLkDPWnPbo1O2rz5q4YgrkbS79rb/zx5ZSJKaDAtJUpNhIUlqMiwkSU2GhSSpaY8JiyQnJ/l2ks1JVo+7HkmaT/aIsEiyD/Bx4BTgCODMJEeMtypJmj/2lOcsjgU2V9V9AEmuBk4F7h5rVZI0JqN+jiNVNZQVz6YkbwdOrqp3d+PvAF5TVef2zbMKWNWNvgr49m5sciEw9U9i7zXf9nm+7S+4z/PF7uzzL1TVoqkm7ClHFk1VdRlw2WysK8nGqpqYjXXtKebbPs+3/QX3eb4Y1j7vEdcsgK3Asr7xpV2bJGkE9pSwuBlYkeSwJC8EzgDWjbkmSZo39ojTUFX1dJJzgeuBfYC1VXXXEDc5K6ez9jDzbZ/n2/6C+zxfDGWf94gL3JKk8dpTTkNJksbIsJAkNRkWfeZblyJJliX5apK7k9yV5H3jrmlUkuyT5LYkXxp3LaOQ5MAk1yb5VpJ7kvzyuGsatiR/0P27vjPJ55K8eNw1zbYka5NsT3JnX9vBSTYkubf7Pmg2tmVYdOZplyJPA++vqiOA44Bz5sE+T3ofcM+4ixihjwF/V1WHA69mL9/3JEuA9wITVfVv6N0Yc8Z4qxqKTwEn79S2GrihqlYAN3Tju82weNY/dylSVU8Bk12K7LWqaltV3doNP0HvF8iS8VY1fEmWAm8BLh93LaOQ5OeBfw98EqCqnqqq/zfWokZjAbBfkgXA/sBDY65n1lXV14HHdmo+FbiiG74COG02tmVYPGsJ8GDf+BbmwS/OSUmWA0cB3xxzKaPwp8B/Bf5pzHWMymHADuB/dKfeLk9ywLiLGqaq2gr8CfBdYBvwg6r68nirGpnFVbWtG34YWDwbKzUsRJKXAJ8Hzquqx8ddzzAl+XVge1XdMu5aRmgBcDRwaVUdBfyIWTo1MVd15+lPpReULwMOSPJ7461q9Kr3bMSsPB9hWDxrXnYpkmRfekFxVVVdN+56RuB44K1J7qd3qvENST4z3pKGbguwpaomjxqvpRcee7NfA75TVTuq6qfAdcCvjLmmUXkkyaEA3ff22VipYfGsedelSJLQO499T1VdNO56RqGqPlhVS6tqOb2f8d9X1V79F2dVPQw8mORVXdOJ7P3d+38XOC7J/t2/8xPZyy/q91kHrOyGVwJfnI2V7hHdfYzCGLoUmQuOB94B3JFkU9d2flWtH19JGpL/BFzV/SF0H3DWmOsZqqr6ZpJrgVvp3fV3G3th1x9JPgecACxMsgW4AFgDXJPkbOAB4PRZ2ZbdfUiSWjwNJUlqMiwkSU2GhSSpybCQJDUZFpKkJsNC816SZ5Js6noo/cck70/ygm7aRJJLdrHs8iS/s4vpL+tu4STJu5L82Qxre1eSl/WNXz6POnvUHOJzFhI8WVVHAiQ5BPgs8HPABVW1Edi4i2WXA7/TLfMzkiyoqoeAt+9Gbe8C7qTrBK+q3r0b65KeN48spD5VtR1YBZybnhMm33mR5HXdEcimrkO+l9J7AOq1XdsfdEcC65L8PXBDd+RxZ98mliX5h+5dAxd06/2ZeZJ8IMmFSd4OTNB7mG5Tkv26ZSe6+c5Mckf3voaP9C3/wyQf7o6SbkwyKx3JaX4zLKSdVNV99J7iP2SnSR8AzumOQl4LPEmvQ77/XVVHVtXF3XxHA2+vqtdNsfpjgd8Cfgn47clf/NPUcS29o5rf7db/5OS07tTUR4A3AEcCxyQ5rZt8AHBjVb0a+DrwngF3XZqWYSEN7hvARUneCxxYVU9PM9+Gqtr5HQP9077X/eK/DvjV51nLMcA/dB3lPQ1cRe+dFQBPAZNvALyF3qkyabcYFtJOkrwCeIadeuusqjXAu4H9gG8kOXyaVfxoF6vfuX+dotd3Uf//xd19/edP69l+fJ7Ba5OaBYaF1CfJIuAvgD+rnTpOS/LKqrqjqj5Cr5fiw4EngJfOYBNv7N6RvB+9N5h9A3gEOCTJv0jyIuDX++afbv03Aa9LsrB7JfCZwNdmUIc0I/7FIfVevbkJ2JfeX/mfBqbqsv28JK+n94a9u4C/7YafSfKP9N6H/P3Gtm6i9/6QpcBnurutSPKhbtpW4Ft9838K+IskTwK/PNlYVduSrAa+CgT4m6qala6opanY66wkqcnTUJKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqen/AwWwvsRRV4QCAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# 성공확률이 0.5인 동전던지기에서 10번 수행시 성공확률\n",
    "n = 10\n",
    "p = 0.5\n",
    "rv = sp.stats.binom(n=n,p=p)\n",
    "print(f\"f(1)={rv.pmf(1):.3f}, f(8)={rv.pmf(8):.3f}\")\n",
    "print(f\"F(1)={rv.cdf(1):.3f}, F(8)={rv.cdf(8):.3f}\")\n",
    "print(f\"E(X)={rv.mean():.3f}, V(X)={rv.var():.3f}\")\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, kde=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 기하분포 (Geometric Distribution)\n",
    "\n",
    "베르누이 시행에서 처음 성공할때까지 반복한 시행 횟수가 따르는 분포\n",
    "\n",
    "**확률질량함수**\n",
    "\n",
    "성공 확률이 p이고, 확률변수의 값이 1 이상인 정수일때(기하분포는 첫성공 후, 연속 실패 가능성이 있기 때문),\n",
    "\n",
    "$$f(x) = (1-p)^{(x-1)}p \\quad (x \\in {1, 2, ... n})$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = \\frac{1}{p} \\quad V(X) = \\frac{(1-p)}{p^2}$$\n",
    "\n",
    "![](https://upload.wikimedia.org/wikipedia/commons/thumb/4/4b/Geometric_pmf.svg/450px-Geometric_pmf.svg.png)\n",
    "\n",
    "https://en.wikipedia.org/wiki/Geometric_distribution\n",
    "\n",
    "**Further Reading**\n",
    "* [Geometric distribution](https://en.wikipedia.org/wiki/Geometric_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "f(1)=0.500, f(8)=0.004\n",
      "F(1)=0.500, F(8)=0.996\n",
      "E(X)=2.000, V(X)=2.000\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 10,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAEGCAYAAACUzrmNAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAVa0lEQVR4nO3de7SddX3n8fcHggoUBUxgMGEabLNgaCuXCReHWhXKxUuBmUEHazU4aGatwal27KqhM6s4WmbBmhlR6lTLCGPAC1KqJWNpNXLRGdcgJIBcZZKiSMIlgSBQpWLwO3/sX+wmnJNnJ+fss8/Jeb/WOus8z/e57O+zVpJPnsv+PakqJEnall1G3YAkafozLCRJnQwLSVInw0KS1MmwkCR1mjPqBoZh7ty5tXDhwlG3IUkzyurVqx+rqnljLdspw2LhwoWsWrVq1G1I0oyS5IHxlnkZSpLUybCQJHUyLCRJnQwLSVKnoYZFku8nuTPJ7UlWtdq+SVYmWdN+79PqSXJxkrVJ7khyZN9+lrT11yRZMsyeJUkvNBVnFq+vqsOranGbXwZcV1WLgOvaPMAbgEXtZynwSeiFC3AecAxwNHDeloCRJE2NUVyGOg1Y3qaXA6f31S+vnpuAvZMcAJwMrKyqTVX1BLASOGWKe5akWW3YYVHA15KsTrK01favqofb9CPA/m16PvBg37brWm28+vMkWZpkVZJVGzdunMxjkKRZb9hfyvv1qlqfZD9gZZLv9i+sqkoyKS/UqKpLgEsAFi9e7Es6JGkSDTUsqmp9+70hyZfp3XN4NMkBVfVwu8y0oa2+Hjiwb/MFrbYeeN1W9RuH2fcFtz02Zn3ZEXOH+bGSNG0N7TJUkj2T7LVlGjgJuAtYAWx5omkJcE2bXgG8sz0VdSzwZLtc9VXgpCT7tBvbJ7WaJGmKDPPMYn/gy0m2fM7nq+pvktwCXJXkbOAB4K1t/WuBNwJrgR8D7wKoqk1JPgLc0tb7cFVtGmLfkqStDC0squp+4LAx6o8DJ4xRL+CccfZ1GXDZZPcoSRqM3+CWJHUyLCRJnQwLSVInw0KS1MmwkCR1MiwkSZ0MC0lSJ8NCktTJsJAkdTIsJEmdDAtJUifDQpLUybCQJHUyLCRJnQwLSVInw0KS1MmwkCR1MiwkSZ0MC0lSJ8NCktTJsJAkdTIsJEmdDAtJUifDQpLUybCQJHUyLCRJnQwLSVInw0KS1MmwkCR1MiwkSZ0MC0lSJ8NCktRp6GGRZNcktyX5Sps/KMm3k6xN8sUkL2r1F7f5tW35wr59nNvq9yU5edg9S5KebyrOLN4H3Ns3fyFwUVX9MvAEcHarnw080eoXtfVIcihwJvArwCnAnybZdQr6liQ1Qw2LJAuANwGfbvMBjgeubqssB05v06e1edryE9r6pwFXVtVPqup7wFrg6GH2LUl6vmGfWXwM+APgZ23+5cAPq2pzm18HzG/T84EHAdryJ9v6P6+PsY0kaQoMLSySvBnYUFWrh/UZW33e0iSrkqzauHHjVHykJM0awzyzOA44Ncn3gSvpXX76OLB3kjltnQXA+ja9HjgQoC1/GfB4f32MbX6uqi6pqsVVtXjevHmTfzSSNIsNLSyq6tyqWlBVC+ndoL6+qt4O3ACc0VZbAlzTple0edry66uqWv3M9rTUQcAi4OZh9S1JeqE53atMug8CVyb5Y+A24NJWvxS4IslaYBO9gKGq7k5yFXAPsBk4p6qem/q2JWn2mpKwqKobgRvb9P2M8TRTVf098JZxtj8fOH94HUqStsVvcEuSOhkWkqROhoUkqZNhIUnqZFhIkjoZFpKkToaFJKmTYSFJ6mRYSJI6GRaSpE6GhSSpk2EhSepkWEiSOhkWkqROhoUkqZNhIUnqZFhIkjoZFpKkToaFJKmTYSFJ6mRYSJI6GRaSpE6GhSSpk2EhSepkWEiSOhkWkqROhoUkqZNhIUnqZFhIkjoZFpKkTgOFRZJfG3YjkqTpa9Aziz9NcnOSf5vkZUPtSJI07QwUFlX1GuDtwIHA6iSfT3LiUDuTJE0bA9+zqKo1wH8EPgi8Frg4yXeT/Iux1k/yknY28p0kdyf5T61+UJJvJ1mb5ItJXtTqL27za9vyhX37OrfV70ty8gSOV5K0Awa9Z/GqJBcB9wLHA79VVf+kTV80zmY/AY6vqsOAw4FTkhwLXAhcVFW/DDwBnN3WPxt4otUvauuR5FDgTOBXgFPoXRLbdXsPVJK04wY9s/gT4FbgsKo6p6puBaiqh+idbbxA9fxdm92t/RS9gLm61ZcDp7fp09o8bfkJSdLqV1bVT6rqe8Ba4OgB+5YkTYJBw+JNwOer6hmAJLsk2QOgqq4Yb6Mkuya5HdgArAT+FvhhVW1uq6wD5rfp+cCDbZ+bgSeBl/fXx9im/7OWJlmVZNXGjRsHPCxJ0iAGDYuvA7v3ze/RattUVc9V1eHAAnpnA4dsb4ODqqpLqmpxVS2eN2/esD5GkmalQcPiJX2XlGjTewz6IVX1Q+AG4NXA3knmtEULgPVtej29p61oy18GPN5fH2MbSdIUGDQsfpTkyC0zSf4p8My2NkgyL8nebXp34ER6N8hvAM5oqy0BrmnTK9o8bfn1VVWtfmZ7WuogYBFw84B9S5ImwZzuVQB4P/DnSR4CAvwj4F91bHMAsLw9ubQLcFVVfSXJPcCVSf4YuA24tK1/KXBFkrXAJnpPQFFVdye5CrgH2AycU1XPDXqAkqSJGygsquqWJIcAB7fSfVX1045t7gCOGKN+P2M8zVRVfw+8ZZx9nQ+cP0ivkqTJN+iZBcBRwMK2zZFJqKrLh9KVJGlaGSgsklwB/BJwO7DlElABhoUkzQKDnlksBg5tN5wlSbPMoE9D3UXvprYkaRYa9MxiLnBPkpvpjfkEQFWdOpSuJEnTyqBh8aFhNiFJmt4GfXT2G0l+EVhUVV9v40I58qskzRKDDlH+Hnojwf5ZK80H/nJIPUmSpplBb3CfAxwHPAU/fxHSfsNqSpI0vQwaFj+pqme3zLSB/nyMVpJmiUHD4htJ/hDYvb17+8+B/zW8tiRJ08mgYbEM2AjcCfwb4FrGeUOeJGnnM+jTUD8D/kf7kSTNMoOODfU9xrhHUVWvnPSOJEnTzvaMDbXFS+gNJb7v5LcjSZqOBr0M9fhWpY8lWQ380eS3tPO74LbHxqwvO2LuFHciSYMZ9DLUkX2zu9A709ied2FIkmawQf/B/29905uB7wNvnfRuJEnT0qCXoV4/7EYkSdPXoJeh/v22llfVRyenHUnSdLQ9T0MdBaxo878F3AysGUZTkqTpZdCwWAAcWVVPAyT5EPBXVfU7w2pMkjR9DDrcx/7As33zz7aaJGkWGPTM4nLg5iRfbvOnA8uH0pEkadoZ9Gmo85P8NfCaVnpXVd02vLYkSdPJoJehAPYAnqqqjwPrkhw0pJ4kSdPMoK9VPQ/4IHBuK+0GfHZYTUmSppdBzyz+OXAq8COAqnoI2GtYTUmSppdBw+LZqiraMOVJ9hxeS5Kk6WbQsLgqyZ8Beyd5D/B1fBGSJM0anU9DJQnwReAQ4CngYOCPqmrlkHuTJE0TnWFRVZXk2qr6NcCAkKRZaNDLULcmOWqonUiSpq1Bw+IY4KYkf5vkjiR3JrljWxskOTDJDUnuSXJ3kve1+r5JViZZ037v0+pJcnGSte0zjuzb15K2/pokS3b0YCVJO2abl6GS/OOq+gFw8g7sezPwgaq6NclewOokK4GzgOuq6oIky4Bl9L7D8QZgUfs5BvgkcEySfYHz6I18W20/K6rqiR3oSZK0A7rOLP4SoKoeAD5aVQ/0/2xrw6p6uKpubdNPA/cC84HT+IdxpZbTG2eKVr+8em6i9+TVAfSCamVVbWoBsRI4ZTuPU5I0AV1hkb7pV+7ohyRZCBwBfBvYv6oebose4R9Gr50PPNi32bpWG6++9WcsTbIqyaqNGzfuaKuSpDF0hUWNMz2wJL8A/AXw/qp66nk77/ui30RV1SVVtbiqFs+bN28ydilJarrC4rAkTyV5GnhVm34qydNJnurYliS70QuKz1XVl1r50XZ5ifZ7Q6uvBw7s23xBq41XlyRNkW2GRVXtWlUvraq9qmpOm94y/9Jtbdu+zHcpcO9W7+heAWx5omkJcE1f/Z3tqahjgSfb5aqvAicl2ac9OXVSq0mSpsigLz/aEccB7wDuTHJ7q/0hcAG94UPOBh4A3tqWXQu8EVgL/Bh4F0BVbUryEeCWtt6Hq2rTEPuWJG1laGFRVf+H598g73fCGOsXcM44+7oMuGzyupMkbY/tefmRJGmWMiwkSZ0MC0lSJ8NCktTJsJAkdTIsJEmdDAtJUifDQpLUybCQJHUyLCRJnQwLSVInw0KS1MmwkCR1MiwkSZ0MC0lSJ8NCktTJsJAkdTIsJEmdDAtJUifDQpLUybCQJHUyLCRJnQwLSVInw0KS1GnOqBvQ5LvgtsfGrC87Yu4UdyJpZ+GZhSSpk2EhSepkWEiSOhkWkqROhoUkqZNhIUnqZFhIkjoZFpKkTkMLiySXJdmQ5K6+2r5JViZZ037v0+pJcnGStUnuSHJk3zZL2vprkiwZVr+SpPEN88ziM8ApW9WWAddV1SLgujYP8AZgUftZCnwSeuECnAccAxwNnLclYCRJU2doYVFV3wQ2bVU+DVjeppcDp/fVL6+em4C9kxwAnAysrKpNVfUEsJIXBpAkacim+p7F/lX1cJt+BNi/Tc8HHuxbb12rjVd/gSRLk6xKsmrjxo2T27UkzXIju8FdVQXUJO7vkqpaXFWL582bN1m7lSQx9WHxaLu8RPu9odXXAwf2rbeg1carS5Km0FSHxQpgyxNNS4Br+urvbE9FHQs82S5XfRU4Kck+7cb2Sa0mSZpCQ3ufRZIvAK8D5iZZR++ppguAq5KcDTwAvLWtfi3wRmAt8GPgXQBVtSnJR4Bb2nofrqqtb5pLkoZsaGFRVW8bZ9EJY6xbwDnj7Ocy4LJJbE2StJ38BrckqZNhIUnqZFhIkjoZFpKkToaFJKmTYSFJ6mRYSJI6GRaSpE6GhSSp09C+wa2d2wW3PTZmfdkRc6e4E0lTwTMLSVInw0KS1MmwkCR1MiwkSZ0MC0lSJ8NCktTJsJAkdTIsJEmdDAtJUifDQpLUybCQJHUyLCRJnQwLSVInR53VtOSottL04pmFJKmTYSFJ6mRYSJI6GRaSpE6GhSSpk09DaVbyaStp+3hmIUnqZFhIkjp5GUqaYl4C00w0Y84skpyS5L4ka5MsG3U/kjSbzIgziyS7Av8dOBFYB9ySZEVV3TPazqTpxzMXDcOMCAvgaGBtVd0PkORK4DTAsJCm2HhhBJMXSAbe9JOqGnUPnZKcAZxSVe9u8+8Ajqmq9/atsxRY2mYPBu6b8ka3z1xg/L91M8vOciw7y3GAxzJdTfdj+cWqmjfWgplyZtGpqi4BLhl1H4NKsqqqFo+6j8mwsxzLznIc4LFMVzP5WGbKDe71wIF98wtaTZI0BWZKWNwCLEpyUJIXAWcCK0bckyTNGjPiMlRVbU7yXuCrwK7AZVV194jbmqgZc8lsADvLsewsxwEey3Q1Y49lRtzgliSN1ky5DCVJGiHDQpLUybCYQkkOTHJDknuS3J3kfaPuaaKS7JrktiRfGXUvE5Fk7yRXJ/luknuTvHrUPe2oJL/X/nzdleQLSV4y6p4GleSyJBuS3NVX2zfJyiRr2u99RtnjIMY5jv/S/nzdkeTLSfYeYYvbzbCYWpuBD1TVocCxwDlJDh1xTxP1PuDeUTcxCT4O/E1VHQIcxgw9piTzgd8FFlfVr9J7IOTM0Xa1XT4DnLJVbRlwXVUtAq5r89PdZ3jhcawEfrWqXgX8P+DcqW5qIgyLKVRVD1fVrW36aXr/IM0fbVc7LskC4E3Ap0fdy0QkeRnwG8ClAFX1bFX9cKRNTcwcYPckc4A9gIdG3M/AquqbwKatyqcBy9v0cuD0qexpR4x1HFX1tara3GZvovd9sRnDsBiRJAuBI4Bvj7iVifgY8AfAz0bcx0QdBGwE/me7pPbpJHuOuqkdUVXrgf8K/AB4GHiyqr422q4mbP+qerhNPwLsP8pmJsm/Bv561E1sD8NiBJL8AvAXwPur6qlR97MjkrwZ2FBVq0fdyySYAxwJfLKqjgB+xMy41PEC7Xr+afQC8BXAnkl+Z7RdTZ7qPes/o5/3T/If6F2S/tyoe9kehsUUS7IbvaD4XFV9adT9TMBxwKlJvg9cCRyf5LOjbWmHrQPWVdWWs7yr6YXHTPSbwPeqamNV/RT4EvDPRtzTRD2a5ACA9nvDiPvZYUnOAt4MvL1m2JfcDIsplCT0rovfW1UfHXU/E1FV51bVgqpaSO8G6vVVNSP/B1tVjwAPJjm4lU5g5g5//wPg2CR7tD9vJzBDb9b3WQEsadNLgGtG2MsOS3IKvcu2p1bVj0fdz/YyLKbWccA76P0v/Pb288ZRNyUA/h3wuSR3AIcD/3m07eyYdnZ0NXArcCe9v+MzZoiJJF8A/i9wcJJ1Sc4GLgBOTLKG3pnTBaPscRDjHMcngL2Ale3v/qdG2uR2crgPSVInzywkSZ0MC0lSJ8NCktTJsJAkdTIsJEmdDAvNakmea48x3p3kO0k+kGSXtmxxkou3se3CJL+9jeWvSHJ1mz4rySe2s7ezkryib/7TO8HAk5qhZsRrVaUheqaqDgdIsh/weeClwHlVtQpYtY1tFwK/3bZ5niRzquoh4IwJ9HYWcBdtIMCqevcE9iVNiGcWUlNVG4ClwHvT87ot7+lI8tq+L1LelmQvel8Oe02r/V47E1iR5HrgunbmcVffRxyY5Mb2Xobz2n6ft06S30/yoSRnAIvpfVHw9iS7t20Xt/XeluTO9s6KC/u2/7sk57ezpJuS7AyD7mkaMCykPlV1P713QOy31aLfB85pZyGvAZ6hN9jg/66qw6vqorbekcAZVfXaMXZ/NPAvgVcBb9nyD/84fVxN76zm7W3/z2xZ1i5NXQgcT+/b5kclOb0t3hO4qaoOA74JvGfAQ5e2ybCQBvMt4KNJfhfYu++9BFtbWVVbv4+hf9nj7R/+LwG/voO9HAXc2AYL3DJ66W+0Zc8CW95auJrepTJpwgwLqU+SVwLPsdXIplV1AfBuYHfgW0kOGWcXP9rG7rceW6foDVXd//dwoq9A/WnfaKbP4X1JTRLDQmqSzAM+BXxi6+Gjk/xSVd1ZVRcCtwCHAE/TGxhuUCe290nvTu9tb98CHgX2S/LyJC+mN3z1FuPt/2bgtUnmJtkVeBvwje3oQ9pu/q9Ds93uSW4HdqP3v/wrgLGGj39/ktfTeyvg3fTecvYz4Lkk36H3zuUnOj7rZnrvMlkAfLY9bUWSD7dl64Hv9q3/GeBTSZ4BXr2lWFUPJ1kG3AAE+KuqmpHDdmvmcNRZSVInL0NJkjoZFpKkToaFJKmTYSFJ6mRYSJI6GRaSpE6GhSSp0/8HvfMRJoXOlJgAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# 성공확률이 0.5인 동전던지기에서 x번 시행시 성공할 확률\n",
    "p = 0.5\n",
    "rv = sp.stats.geom(p=p)\n",
    "print(f\"f(1)={rv.pmf(1):.3f}, f(8)={rv.pmf(8):.3f}\")\n",
    "print(f\"F(1)={rv.cdf(1):.3f}, F(8)={rv.cdf(8):.3f}\")\n",
    "print(f\"E(X)={rv.mean():.3f}, V(X)={rv.var():.3f}\")\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, kde=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 포아송 분포 (Poisson Distribution)\n",
    "\n",
    "시행 횟수가 많고, 사상 발생의 확률은 아주 작은 이항분포, 단위 시간 또는 단위 공간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산 확률 분포\n",
    "\n",
    "**확률질량함수**\n",
    "\n",
    "정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값이 $\\lambda = np$ 일때, 그 사건이 x 회 일어날 확률  \n",
    "\n",
    "$$f(x) = \\frac{\\lambda^x e^{-\\lambda}}{x!} \\quad (x \\in {0, 1, 2, ... n})$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = \\lambda \\quad V(X) = \\lambda$$\n",
    "\n",
    "$\\lambda$ 값이 커질 수록 정규분포에 가까워짐\n",
    "\n",
    "![](https://upload.wikimedia.org/wikipedia/commons/thumb/1/16/Poisson_pmf.svg/325px-Poisson_pmf.svg.png)\n",
    "\n",
    "https://en.wikipedia.org/wiki/Poisson_distribution\n",
    "\n",
    "**Further Reading**\n",
    "* [Poisson distribution](https://en.wikipedia.org/wiki/Poisson_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 11,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "f(1)=0.271, f(8)=0.001\n",
      "F(1)=0.406, F(8)=1.000\n",
      "E(X)=2.000, V(X)=2.000\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 11,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAEGCAYAAACUzrmNAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAUTklEQVR4nO3df7DddX3n8edLQAWkBTYhCwnboJPK0lZJ9oJ0qesPVsQfFdxaF1oVGTWdWVila2cbmc7i2GEmzlioVJcWMSsoylLEmm3T0kCtbjuDECAFAjpkECQhQhBXqDJi6Hv/ON9rTkLu/ZwL99xzkvt8zNy53/P5fr7f875nkvu6n++PzzdVhSRJ03nBqAuQJI0/w0KS1GRYSJKaDAtJUpNhIUlq2n/UBQzDggULaunSpaMuQ5L2KrfddttjVbVwT+v2ybBYunQpGzZsGHUZkrRXSfLgVOs8DCVJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWraJ+/g1sytvuOxgfqtWr5gyJVIGkeOLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUpP3WYwR73WQNK4cWUiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUNLSwSHJ0kq8luSfJpiQf6to/mmRrko3d15v7tvlIks1Jvp3kjX3tp3Vtm5OsGlbNkqQ9G+Yd3DuAD1fV7UkOAW5Lsr5bd0lVfaK/c5LjgDOBXwKOAm5M8ovd6k8DbwC2ALcmWVtV9wyxdklSn6GFRVVtA7Z1y08muRdYPM0mpwPXVNVPgO8k2Qyc2K3bXFX3AyS5putrWEjSHJmTcxZJlgLLgW92TecluTPJmiSHdW2LgYf6NtvStU3Vvvt7rEyyIcmG7du3z/aPIEnz2tDDIslLgC8D51fVE8BlwMuA4+mNPP5oNt6nqi6vqomqmli4cOFs7FKS1BnqrLNJDqAXFFdX1fUAVfVI3/rPAH/ZvdwKHN23+ZKujWnaJUlzYJhXQwX4LHBvVV3c135kX7e3A3d3y2uBM5O8KMkxwDLgFuBWYFmSY5K8kN5J8LXDqluS9GzDHFmcDLwbuCvJxq7tAuCsJMcDBTwA/A5AVW1Kci29E9c7gHOr6hmAJOcBNwD7AWuqatMQ65Yk7WaYV0P9A5A9rFo3zTYXARftoX3ddNtJkobLO7glSU2GhSSpybCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWoyLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSpybCQJDUZFpKkpqGFRZKjk3wtyT1JNiX5UNd+eJL1Se7rvh/WtSfJpUk2J7kzyYq+fZ3d9b8vydnDqlmStGfDHFnsAD5cVccBJwHnJjkOWAXcVFXLgJu61wBvApZ1XyuBy6AXLsCFwKuAE4ELJwNGkjQ3hhYWVbWtqm7vlp8E7gUWA6cDV3bdrgTO6JZPB66qnpuBQ5McCbwRWF9Vj1fVD4D1wGnDqluS9Gxzcs4iyVJgOfBNYFFVbetWfQ9Y1C0vBh7q22xL1zZV++7vsTLJhiQbtm/fPrs/gCTNc0MPiyQvAb4MnF9VT/Svq6oCajbep6our6qJqppYuHDhbOxSktQZalgkOYBeUFxdVdd3zY90h5fovj/atW8Fju7bfEnXNlW7JGmODPNqqACfBe6tqov7Vq0FJq9oOhv4al/7e7qrok4CftgdrroBODXJYd2J7VO7NknSHNl/iPs+GXg3cFeSjV3bBcBq4Nok7wMeBN7ZrVsHvBnYDPwYOAegqh5P8ofArV2/j1XV40OsW5K0m6GFRVX9A5ApVp+yh/4FnDvFvtYAa2avOknSTHgHtySpybCQJDUZFpKkJsNCktQ0zKuhpFmz+o7HBuq3avmCIVcizU+OLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUtNAYZHkV4ZdiCRpfA06svifSW5J8l+S/PxQK5IkjZ2BwqKqXg38Nr0n1t2W5ItJ3jDUyiRJY2PgcxZVdR/wB8DvA68BLk3yrST/aVjFSZLGw6DnLF6R5BLgXuD1wK9X1b/tli8ZYn2SpDEw6ESCfwJcAVxQVU9NNlbVw0n+YCiVSZLGxqBh8Rbgqap6BiDJC4AXV9WPq+rzQ6tOkjQWBj1ncSNwYN/rg7o2SdI8MGhYvLiq/nnyRbd80HBKkiSNm0HD4kdJVky+SPLvgKem6S9J2ocMes7ifODPkzwMBPjXwH8eVlGSpPEyUFhU1a1JjgVe3jV9u6p+OryyJEnjZCbP4D4BWNptsyIJVXXVUKqSJI2VgcIiyeeBlwEbgWe65gIMC0maBwYdWUwAx1VVDbMYSdJ4GvRqqLvpndSWJM1Dg44sFgD3JLkF+MlkY1W9bShVSZLGyqBh8dGZ7jjJGuCtwKNV9ctd20eBDwDbu24XVNW6bt1HgPfROyfywaq6oWs/DfgksB9wRVWtnmktkqTnZ9BLZ7+e5BeAZVV1Y5KD6P3yns7ngE/x7JPgl1TVJ/obkhwHnAn8EnAUcGOSX+xWfxp4A7AFuDXJ2qq6Z5C6JUmzY9Apyj8AXAf8Wde0GPiL6bapqm8Ajw9Yx+nANVX1k6r6DrAZOLH72lxV91fV08A1XV9J0hwa9AT3ucDJwBPwswchHfEc3/O8JHcmWZPksK5tMfBQX58tXdtU7c+SZGWSDUk2bN++fU9dJEnP0aBh8ZPuL3sAkuxP7z6LmbqM3v0axwPbgD96DvvYo6q6vKomqmpi4cKFs7VbSRKDh8XXk1wAHNg9e/vPgf8z0zerqkeq6pmq+hfgM/QOMwFspfd870lLurap2iVJc2jQsFhF7wqmu4DfAdbRex73jCQ5su/l2+ndvwGwFjgzyYuSHAMsA24BbgWWJTkmyQvpnQRfO9P3lSQ9P4NeDTU5EvjMoDtO8iXgtcCCJFuAC4HXJjme3iGsB+gFD1W1Kcm1wD3ADuDcvqfynQfcQO/qqzVVtWnQGiRJs2PQuaG+wx7OUVTVS6fapqrO2kPzZ6fpfxFw0R7a19EbyUiSRmQmc0NNejHwm8Dhs1+OJGkcDXTOoqq+3/e1tar+GHjLcEuTJI2LQQ9Dreh7+QJ6I42ZPAtDkrQXG/QXfv/9EDvonZx+56xXI0kaS4NeDfW6YRciSRpfgx6G+m/Tra+qi2enHEnSOJrJ1VAnsPOGuF+nd9PcfcMoatRW3/HYQP1WLV8w5EokaTwMGhZLgBVV9ST87LkUf1VV7xpWYZKk8THodB+LgKf7Xj/dtUmS5oFBRxZXAbck+Ur3+gzgyqFUJEkaO4NeDXVRkr8GXt01nVNVdwyvLEnSOBn0MBTAQcATVfVJYEs3O6wkaR4Y9LGqFwK/D3ykazoA+MKwipIkjZdBRxZvB94G/Aigqh4GDhlWUZKk8TJoWDxdVUU3TXmSg4dXkiRp3AwaFtcm+TPg0CQfAG5kBg9CkiTt3ZpXQyUJ8L+BY4EngJcD/6Oq1g+5NknSmGiGRVVVknVV9SuAASFJ89Cgh6FuT3LCUCuRJI2tQe/gfhXwriQP0LsiKvQGHa8YVmGSpPExbVgk+TdV9V3gjXNUjyRpDLVGFn9Bb7bZB5N8uap+Yw5qkiSNmdY5i/Qtv3SYhUiSxlcrLGqKZUnSPNI6DPXKJE/QG2Ec2C3DzhPcPzfU6iRJY2HasKiq/eaqEEnS+JrJFOWSpHnKsJAkNQ0tLJKsSfJokrv72g5Psj7Jfd33w7r2JLk0yeYkdyZZ0bfN2V3/+5KcPax6JUlTG+bI4nPAabu1rQJuqqplwE3da4A3Acu6r5XAZdALF+BCeneQnwhcOBkwkqS5M7SwqKpvAI/v1nw6cGW3fCVwRl/7VdVzM72p0I+kd+f4+qp6vKp+QG8iw90DSJI0ZHN9zmJRVW3rlr8HLOqWFwMP9fXb0rVN1f4sSVYm2ZBkw/bt22e3akma50Z2grv/yXuztL/Lq2qiqiYWLlw4W7uVJDH3YfFId3iJ7vujXftW4Oi+fku6tqnaJUlzaK7DYi0weUXT2cBX+9rf010VdRLww+5w1Q3AqUkO605sn9q1SZLm0KDPs5ixJF8CXgssSLKF3lVNq+k9z/t9wIPAO7vu64A3A5uBHwPnAFTV40n+ELi16/exqtr9pLkkaciGFhZVddYUq07ZQ98Czp1iP2uANbNYmiRphryDW5LUZFhIkpoMC0lS09DOWUj7itV3PDZQv1XLFwy5Eml0HFlIkpoMC0lSk2EhSWoyLCRJTYaFJKnJsJAkNRkWkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSpybCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUNJKwSPJAkruSbEyyoWs7PMn6JPd13w/r2pPk0iSbk9yZZMUoapak+WyUI4vXVdXxVTXRvV4F3FRVy4CbutcAbwKWdV8rgcvmvFJJmufG6TDU6cCV3fKVwBl97VdVz83AoUmOHEF9kjRvjSosCvjbJLclWdm1Laqqbd3y94BF3fJi4KG+bbd0bbtIsjLJhiQbtm/fPqy6JWle2n9E7/trVbU1yRHA+iTf6l9ZVZWkZrLDqrocuBxgYmJiRttKkqY3kpFFVW3tvj8KfAU4EXhk8vBS9/3RrvtW4Oi+zZd0bZKkOTLnYZHk4CSHTC4DpwJ3A2uBs7tuZwNf7ZbXAu/proo6Cfhh3+EqSdIcGMVhqEXAV5JMvv8Xq+pvktwKXJvkfcCDwDu7/uuANwObgR8D58x9yZI0v815WFTV/cAr99D+feCUPbQXcO4clCZJmsI4XTorSRpThoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lS06jmhpLUsPqOxwbqt2r5giFXIjmykCQNwLCQJDUZFpKkJsNCktRkWEiSmgwLSVKTYSFJajIsJElNhoUkqcmwkCQ1GRaSpCbDQpLUZFhIkpoMC0lSk2EhSWoyLCRJTT78SNJz5gOa5g9HFpKkJsNCktRkWEiSmgwLSVLTXnOCO8lpwCeB/YArqmr1iEuSNCKeWJ97e8XIIsl+wKeBNwHHAWclOW60VUnS/LG3jCxOBDZX1f0ASa4BTgfuGWlVkuaVQUc0sO+NalJVo66hKck7gNOq6v3d63cDr6qq8/r6rARWdi9fDnz7ebzlAmDwfxX7Nj+LXfl57MrPY6d94bP4hapauKcVe8vIoqmqLgcun419JdlQVROzsa+9nZ/Frvw8duXnsdO+/lnsFecsgK3A0X2vl3RtkqQ5sLeExa3AsiTHJHkhcCawdsQ1SdK8sVcchqqqHUnOA26gd+nsmqraNMS3nJXDWfsIP4td+Xnsys9jp336s9grTnBLkkZrbzkMJUkaIcNCktRkWPRJclqSbyfZnGTVqOsZpSRHJ/laknuSbEryoVHXNGpJ9ktyR5K/HHUto5bk0CTXJflWknuT/OqoaxqlJL/b/T+5O8mXkrx41DXNNsOi45Qiz7ID+HBVHQecBJw7zz8PgA8B9466iDHxSeBvqupY4JXM488lyWLgg8BEVf0yvYtwzhxtVbPPsNjpZ1OKVNXTwOSUIvNSVW2rqtu75Sfp/TJYPNqqRifJEuAtwBWjrmXUkvw88B+AzwJU1dNV9f9GWtTo7Q8cmGR/4CDg4RHXM+sMi50WAw/1vd7CPP7l2C/JUmA58M0RlzJKfwz8d+BfRlzHODgG2A78r+6w3BVJDh51UaNSVVuBTwDfBbYBP6yqvx1tVbPPsNC0krwE+DJwflU9Mep6RiHJW4FHq+q2UdcyJvYHVgCXVdVy4EfAvD3Hl+QwekchjgGOAg5O8q7RVjX7DIudnFJkN0kOoBcUV1fV9aOuZ4ROBt6W5AF6hydfn+QLoy1ppLYAW6pqcqR5Hb3wmK/+I/CdqtpeVT8Frgf+/YhrmnWGxU5OKdInSegdk763qi4edT2jVFUfqaolVbWU3r+Lv6uqfe4vx0FV1feAh5K8vGs6hfn9uIDvAiclOaj7f3MK++AJ/71iuo+5MIIpRcbdycC7gbuSbOzaLqiqdaMrSWPkvwJXd39Y3Q+cM+J6RqaqvpnkOuB2elcR3sE+OPWH031Ikpo8DCVJajIsJElNhoUkqcmwkCQ1GRaSpCbDQvNekmeSbOxmDf2nJB9O8oJu3USSS6fZdmmS35pm/VHdZZUkeW+ST82wtvcmOarv9RVO6KhR8D4LCZ6qquMBkhwBfBH4OeDCqtoAbJhm26XAb3Xb7CLJ/lX1MPCO51Hbe4G76Samq6r3P499Sc+ZIwupT1U9CqwEzkvPayefX5HkNd0IZGM3gd4hwGrg1V3b73YjgbVJ/g64qRt53N33Fkcn+fsk9yW5sNvvLn2S/F6SjyZ5BzBB7+a3jUkO7Lad6PqdleSu7hkKH+/b/p+TXNSNkm5OsmjYn5v2fYaFtJuqup/eXfxH7Lbq94Bzu1HIq4Gn6E2g93+r6viquqTrtwJ4R1W9Zg+7PxH4DeAVwG9O/uKfoo7r6I1qfrvb/1OT67pDUx8HXg8cD5yQ5Ixu9cHAzVX1SuAbwAcG/NGlKRkW0uD+Ebg4yQeBQ6tqxxT91lfV49Os+373i/964NeeYy0nAH/fTV63A7ia3jMmAJ4GJp/mdxu9Q2XS82JYSLtJ8lLgGeDR/vaqWg28HzgQ+Mckx06xix9Ns/vd59cpevMJ9f9ffL6P5Pxp7ZzH5xk8N6lZYFhIfZIsBP4U+FTtNnFakpdV1V1V9XF6sxQfCzwJHDKDt3hDksOTHAicQW+08ghwRJJ/leRFwFv7+k+1/1uA1yRZ0D0S+Czg6zOoQ5oR/+KQeo/D3AgcQO+v/M8De5qW/fwkr6P3tLxNwF93y88k+Sfgc8APGu91C71nhCwBvtBdbUWSj3XrtgLf6uv/OeBPkzwF/OpkY1VtS7IK+BoQ4K+q6quD/8jSzDjrrCSpycNQkqQmw0KS1GRYSJKaDAtJUpNhIUlqMiwkSU2GhSSp6f8DlluP0NVOzIwAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# 평균 불량율이 2인 제품 생산시 불량이 1개(x = 1)발생할 확률\n",
    "p = 0.002\n",
    "n = 1000\n",
    "l = n*p\n",
    "rv = sp.stats.poisson(l)\n",
    "\n",
    "print(f\"f(1)={rv.pmf(1):.3f}, f(8)={rv.pmf(8):.3f}\")\n",
    "print(f\"F(1)={rv.cdf(1):.3f}, F(8)={rv.cdf(8):.3f}\")\n",
    "print(f\"E(X)={rv.mean():.3f}, V(X)={rv.var():.3f}\")\n",
    "\n",
    "# 포아송분포에서 실제 10000개 랜덤 샘플링 후 시각화\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=30, kde=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 연속확률분포\n",
    "\n",
    "확률변수가 취할 수 있는 값이 연속적인 확률변수\n",
    "\n",
    "**확률밀도함수(Probability density function)**\n",
    "\n",
    "확률변수 X 가 취할 수 있는 값에 대한 집합 $X = {x_1, x_2, x_3, ...}$ 일때, 확률변수 X가 $x_k$를 취할 확률\n",
    "\n",
    "$$f(x) = P(x0 \\geq X \\leq x_1) = \\int_{x0}^{x1}f(x)dx $$\n",
    "\n",
    "**누적분포함수(Cumulative distribution function)**\n",
    "\n",
    "확률변수 X가 x이하가 될 때의 확률\n",
    "\n",
    "$$F(x) = P(X \\leq x) = \\int_{- \\infty}^{x}f(x)dx$$ \n",
    "\n",
    "**기대값(Expted value)**\n",
    "\n",
    "확률변수의 평균\n",
    "\n",
    "$$E(X) = \\int_{- \\infty}^{\\infty}xf(x)dx$$\n",
    "\n",
    "**분산(Variance)**\n",
    "\n",
    "$$V(X) = \\int_{- \\infty}^{\\infty}(x - E(X))^2f(x)dx$$"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 연속균등분포 (Continuous Uniform Distribution)\n",
    "\n",
    "사상이 일어나는 확률이 같은 분포, 확률변수가 x = $[\\alpha, \\beta]$ 사이에 연속적인 값을 취할때,\n",
    "\n",
    "\n",
    "**확률밀도함수**\n",
    "\n",
    "$$f(x) = \\frac{1}{\\beta - \\alpha} \\quad (x \\in [\\alpha, \\beta])$$\n",
    "$$f(x) = 0 \\quad (otherwise)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = \\frac{\\alpha + \\beta}{2} \\quad V(X) = \\frac{(\\beta - \\alpha)^2}{12}$$\n",
    "\n",
    "![](https://www.researchgate.net/profile/Lakshmi-Padmaja-Dhyaram/publication/319013233/figure/fig3/AS:525690496917504@1502345789065/Uniform-Distribution-Types.png)\n",
    "\n",
    "https://www.researchgate.net/figure/Uniform-Distribution-Types_fig3_319013233\n",
    "\n",
    "**Further Reading**\n",
    "* [연속균등분포](https://ko.wikipedia.org/wiki/%EC%97%B0%EC%86%8D%EA%B7%A0%EB%93%B1%EB%B6%84%ED%8F%AC)\n",
    "* [Continuous uniform distribution](https://en.wikipedia.org/wiki/Continuous_uniform_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 12,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution '), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 12,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEGCAYAAAB/+QKOAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAog0lEQVR4nO3de5hcd33f8ff3nLntfaWVLFuyZdlYxhgw1JZN2kBM4CGYJGDSmMaQPDUtidMUtyUJbUyaB4ib9MEktZMU+iROoDiGxBA3UCU4cY0hJFxt2VyMsI2Fr5Is67LS3ud6vv3jnFmtVyvt7GpmZ87M5/U8++zMOWd2v7Mz+/vO727ujoiIyGJBuwMQEZHOpAQhIiJLUoIQEZElKUGIiMiSlCBERGRJmXYH0CwbNmzwbdu2tTsMEZFUefDBBw+7+8alznVNgti2bRu7du1qdxgiIqliZk+f7JyamEREZElKECIisiQlCBERWZIShIiILEkJQkRElqQEISIiS1KCEBGRJSlBpJi7U42cSEu2i0gLdM1EuV7g7jwzXeGRo2X2zlQYL9aIknP9GWNjIcOWgQwXjOQ4qz+DmbU1XhFJt5YmCDO7CvhDIAT+zN0/tOj8jwF/AFwCXOvudy04dx3wW8nd33H321sZa6fbN1Phvr0z7J+tkguMcwYzXDCcIx8aVXemKhEH52p8/fk5vvb8HAMZY/tInheP5jh3KEugZCEiK9SyBGFmIfBR4A3AXuABM9vp7t9fcNkzwDuB9y567HrgA8AOwIEHk8cebVW8ncrdefBQkfv2zTCQCXjTOYNcvD5PNli6wJ+rRvxwssyeiTLfP1ri20eK9IXG9tEcF43mOXsgSy5cWbKI3JmtOlOVGtOViOlKxFQlYqYSUao55cipRI5hhAZhYPRnjKFswFA2ZH0+ZGNfSF8m/S2a05WI/TMVnput8txslelKxFw1oliLm/mygZENjEJo9GUC+jJGfyagb8H9vjAgHxq50MgFFt8OjPAkr2kvKFYjnpyqsH+mwuFijdlqhBP/PUdzIRsKIesLIWf2ZxjOBquqHZdrzuFilUPFGrOViHIUv3cDYCAb0J8JGMkFbOrPUAjT/15thlbWIK4A9rj7EwBmdidwNTCfINz9qeRctOixbwTudffx5Py9wFXAX7Yw3o70Twdm+dqBObaP5PjpcwfJL/PG7csEvGx9gZetL1CJnCcnyzx6rMyjR8t890gJAzYUQs4ayDCcDSmERiFjRA6VpKCfSRLAVCViqhwnhMUvkBE3a+XDgFxoZIM4kVQjqFYjnpuJmKm+sG9kMBuwsRCysS/DhkLIxkLIWCGz4oS1ltyd5+dq7JmIk+6BuSoQd95t7AsZK4QUwuMFSv1vWKo5s9WIw8WIuWqFuaqzXE9RaJALTkwcufCFtwMz3MFx3CECapFTdahGTm3+uxNYnLBCO5688mGcwApJoipk4vv5MKAQGpk1SlTuztPTFR46VGTPRJkIyBiMFUIGswGBGaVa3Ky6+2hp/nEDGeOsgSyb+zNs7AsZysbXF8L4fTxTjZgs15gsRxwp1Tg0V+VwscZE+YXvYgNyoRG5U1n0Bt/cn+El6/JcMpZf9n+um7UyQWwBnl1wfy/wqtN47JbFF5nZ9cD1AFu3bl1dlB3s4SNFvnZgjkvW53nT1sEVf2rKBsaFo3kuHM1TjZynpyrsSz79Pj5RZq66dJGVDWAoGzKUDdg6lE1qAgGD2YChXPx9IBMs22xVc2eqHDGe/JMeKsbfHzo0x8JfPZILGMuHjOZD1uVDRvMB63Lx/bUqrBaarkQ8M1Xh6ekyT0xWmEpKjy0DGa48q5+tQ1k29WVWFJt7PWk4c7WIcs0pRU65lnwlt+ePJd9na86xcv366ISCzAAzyJiRCeLvYf27GTWPqLpTi6DiTqXmnORln5cxkiQSUMjY/O2+pJ9rU1+c5Ff72hSrEQ+Pl/jW4SLjpRp9obHjjD4uHMmxeSCz5PuqVIs4UqzN19yem6myZ6K87O8KgPWFkM39GS4Zy7CxELKhkGE4FxAa8/9T5SShj5dq7Jup8MOJCvftm+ErB2Z57eZ+XjlW6Mk+vVR3Urv7bcBtADt27OiqoTxHSzX+/tlpzh3M8sZVJIfFMoHxopEcLxrJzR+L3CnW4oLLOP4JMxvQlH+G0IzRpOA/f/iFv/dYKeJQMf5kd3iumvxjVilFL3wZh7LBCxLGunoSyQUUGmyyco8L3GLNKVadYu1401gpKaCnKnHhMF6sMZmUwvnQOHcwy2tGcrxoOMdAdvWfJM2ST+oZiLvkVqc+Ys1Y/WtUTZ53sRbNv/71v8v8/QW3ZyvOeLHCbNUpR0UgLnjP6MuweSAeGLFlIMtI7uRNP7XIeWKqzO7xEo9PlKl5nHB/+sxBLhrNL5ts8mHA5oGAzQPZ+WPFpECvN3sWa05g0J8JGE4+zIzmwoaa7nKhkQuPv1dfcxbsn6nw5f2z3PPsDE9NVXjLuUM91wzYygSxDzhnwf2zk2ONPva1ix77D02JKgXcnXufnSY0483bhghb9MklsLivoH+NPyYEZqxP2pRfvOC4uzNXc46Vahwt1ThaijhWrnGsVOOHk+UTmqwKobEuH9d0QmP+k2exFjFXTRJCLaJY9ROayBbLh8b6fMg5g1k29oWcm9QSOq1zvxnxZIK4GWmlCc/dmShHHJir8vxslX0zVR4eL/LQ4fj8QMbYPJBlXT5uujTi5p7xYo19s1VKNacvY7xirMAlYwXOPM03XiETsLmF/VqbB7Jce8Ew9x+c40v7Z/kbpnjLtqGOe0+0UiuLhgeA7WZ2HnGBfy3wjgYfew/w381sXXL/J4D3NT/EzvT4RJknpiq8fssAg6fxqTVtbD5hvfCTYl255hwrx8nj2IIEMl6qEXncpAXQlzSNjOQCCpls0t5uFDLB/O18vaM4aZNvR1NW2tiCGuFFo3kgrtEcnKuxf6bCvpm4+efJyfJ8M1Y2gNFcyEWjObaP5DlvONuyDzytYGa8alM/AF/aP8uGA3O8+qz+Nke1dlqWINy9amY3EBf2IfBxd99tZjcBu9x9p5ldDnwWWAe82cx+291f6u7jZvbfiJMMwE31Dute8PXn51iXD7hsY6HdoXSUXGic0ZfhjL5Ut4x2lcCMM/sznNmf4dJkTzL3uKPcifszuqHt/lWb+jkwW+Xrz8/yknU5xgq98R4075JZuDt27PBu2FFu30yFO34wwRvOHuCyjX3tDkdEEtOViD995Cib+jK8Y/tIu8NpGjN70N13LHWud9ovUmLXwTnygfGy9fl2hyIiCwxmA159Zj/PTMfzNXqBEkQHmatGPHaszMt7fOy1SKe6ZCxPPjB2HSq2O5Q1oVKogzyeTBZ62Xr1PYh0onwYcMlYnkePlpgq19odTsspQXSQHxwrM5wN2NS3+nHyItJal23sIwK+O15a9tq0U4LoEOWa8+RUmQtHc10x6kOkW43mQ7YMZPjBMSUIWSNPTMazSy8cUee0SKfbPpLj+bkaE13ezKQE0SF+OFmmEBpnD/bG+GqRNNueLFnTyHpQaaYE0SGena5wzqD2bRBJg7FChvX5kMeVIKTVpisRx8oRZw+o9iCSFttHcjwzVaFc647JxktRgugAz07Hk262Dp64/pCIdKatg1kiYP9s906aU4LoAM9OV8gGsGmtl1UVkVXbktT4981U2xxJ6yhBdIC9MxW2DKj/QSRNCpl4h8S906pBSIuUahEH52qcvcTy1iLS2bYMZNk/U53fyKnbKEG02fNz8Tjqs9S8JJI6Zw9mKEXO4WJ3zodQgmizg3Nx+6X6H0TSp17z79ZmJiWINjs4V6U/Ywxk1P8gkjYjuYD+jHFgtjs7qpUg2uzgbI0z+jJaf0kkhcyMjYUMh9TEJM0WuXOoWNUWmiIpdkZfyKG57uyoVoJoo/FijZrHbzARSaeNfRmqDsdKUbtDaToliDZ6PumgVg1CJL3q/78Hi93XD6EE0UYH52qEBmMF1SBE0mqsEGLAoTklCGmiw8Uq6/MhoTqoRVIrGxjr8yEH57qvo1oJoo2OliLWq/Ygknobk47qbqME0SY1d46VaqzPK0GIpN3GvgzHylHXLf2tBNEmE6WICJQgRLrAWPJ/fLTUXc1MShBtMp68kdTEJJJ+65QgpJnmE4RqECKpV08Q40oQ0gzjxRqF0OjL6CUQSbtcaAxmAtUgpDnG1UEt0lXWFZQgpEmOlmrqfxDpIuvyoZqY5PSVa85UJVINQqSLrM+HzFadUq171mRSgmiDY+X4U8Y6JQiRrnF8JJMSREPM7Coze8zM9pjZjUucz5vZp5Pz3zSzbcnxrJndbmYPm9kjZva+Vsa51iaSBDGSU34W6RbdOJKpZSWUmYXAR4E3ARcDbzezixdd9i7gqLtfANwK3JwcfxuQd/eXA5cBv1xPHt1gIvmEMZJTDUKkW3TjXIhWfoS9Atjj7k+4exm4E7h60TVXA7cnt+8CXm/x1moODJhZBugDysBkC2NdUxPlGhmDfm0zKtI1soExlO2ukUytTBBbgGcX3N+bHFvyGnevAhPAGHGymAGeA54Bft/dxxf/AjO73sx2mdmuQ4cONf8ZtMhEOWIkH2qbUZEuM5wLmCyrD6LVrgBqwGbgPODXzez8xRe5+23uvsPdd2zcuHGtY1y1iXJN/Q8iXWgkF873MXaDVpZS+4BzFtw/Ozm25DVJc9IIcAR4B/D37l5x94PAV4EdLYx1TU2UI/U/iHShkVzAVDnqmv2pW5kgHgC2m9l5ZpYDrgV2LrpmJ3Bdcvsa4Ivu7sTNSq8DMLMB4EeAR1sY65op1SKKNVcNQqQLDecCImC60h3NTC0rpZI+hRuAe4BHgM+4+24zu8nM3pJc9jFgzMz2AL8G1IfCfhQYNLPdxInmf7v7d1sV61qaKGsEk0i3qv9fT3RJP0SmlT/c3e8G7l507P0LbheJh7Quftz0Use7geZAiHSv4eT/erJcA7LtDaYJVEqtMdUgRLrXcLa7ahBKEGtsshxpDoRIl8qFRn/GumaoqxLEGpso1xjOaQ6ESLca7qKhrkoQa2yqHM23U4pI9xnposlyKqnW2FQlYiirP7tItxrOBkyUa3gXzIVQSbWGInemlSBEutpILqTqMFtVgpAVmKlEODCkJiaRrlVvQp7qgslyKqnWUP0NM5TVEFeRblVvIZiqpL+jWgliDU3OJwj92UW61WC9BtEFHdUqqdZQ/Q2jJiaR7jWQCTC6Yz0mlVRraLoSERr0hZoDIdKtAjMGs4H6IGRl6kNcNUlOpLsNKUHISk2Wa2peEukBQzklCFmheA6ERjCJdLvBbMC0OqmlUe6uWdQiPWIoG1CKnFIt3UlCpdUamas6NdcQV5FeUP8/T/tIJpVWa6Q+B2JQfRAiXa/elJz2uRAqrdbIjCbJifSMoS5ZbkOl1RqpVzUHlSBEut5gVglCVmC6Gr9RBjL6k4t0u2xgFEJTgpDGTFciCqGRCTRJTqQXDGUDdVJLY6YrkZqXRHrIQDaY73tMK5VYa2RGCUKkpwyqBiGNmq5E6n8Q6SEDmYCZapTqrUdVYq0Bd2emqhqESC8ZyAbUHIq1Lk8QZvbyVgfSzYq1eBa1EoRI76j/v6e5H6LREut/mdn9ZvbvzWykpRF1Ic2BEOk9A5l4xGJ9iHsaNVRiuftrgJ8HzgEeNLO/MLM3tDSyLqIEIdJ7eqkGgbs/DvwW8BvAlcAfmdmjZvYvWxVct1CCEOk9A12wYF+jfRCXmNmtwCPA64A3u/tLktu3tjC+rlB/g2gUk0jvyAdGxmCmmt5O6kyD1/1P4M+A33T3ufpBd99vZr/Vksi6yHQ1IhcYOe1FLdIzzCz1k+UaTRA/Bcy5ew3AzAKg4O6z7n5Hy6LrEpokJ9Kb0j5ZrtFS6wtA34L7/cmxUzKzq8zsMTPbY2Y3LnE+b2afTs5/08y2LTh3iZl93cx2m9nDZlZoMNaOM12JGMiq9iDSa+qT5dKq0QRRcPfp+p3kdv+pHmBmIfBR4E3AxcDbzeziRZe9Czjq7hcQ92XcnDw2A3wS+Hfu/lLgtUClwVg7zkw1YlD9DyI9p1dqEDNmdmn9jpldBsyd4nqAK4A97v6Eu5eBO4GrF11zNXB7cvsu4PVmZsBPAN919+8AuPuRevNWGs1WfH5Eg4j0joFsQLHmVKN0dlQ32gfxHuCvzGw/YMCZwM8t85gtwLML7u8FXnWya9y9amYTwBhwIeBmdg+wEbjT3T+8+BeY2fXA9QBbt25t8KmsrUrklCLXCCaRHlRvOZipRozkwjZHs3INJQh3f8DMLgJenBx6zN1b2eSTAV4NXA7MAveZ2YPuft+iuG4DbgPYsWNHR6bo+ggG1SBEes/AgslyXZsgEpcD25LHXGpmuPufn+L6fcQzr+vOTo4tdc3epN9hBDhCXNv4R3c/DGBmdwOXAveRMjPaSU6kZw2mfLJcoxPl7gB+n+Of6i8HdizzsAeA7WZ2npnlgGuBnYuu2Qlcl9y+Bviix2vj3gO83Mz6k8RxJfD9RmLtNKpBiPSu+ujFtI5karQGsQO42FewsHnSp3ADcWEfAh93991mdhOwy913Ah8D7jCzPcA4cRLB3Y+a2S3EScaBu9398w0/qw4yX4PQMFeRnlNvOUhrDaLRBPE94o7p51byw939buDuRcfev+B2EXjbSR77SeKhrqk2U4lzar+amER6TmBGf8bmy4G0aTRBbAC+b2b3A6X6QXd/S0ui6iIz1Yi+jBGaahAivWggE6R2ye9GE8QHWxlEN5vRVqMiPW0wxesxNTrM9ctmdi6w3d2/YGb9xP0KsoyZqhKESC8byAYcKaZzIYhGRzH9EvFM5z9JDm0BPteimLqKFuoT6W2DSRPTCsb4dIxGS653Az8KTML85kFntCqobuHuzFQj+jPqfxDpVQPZgMjjvenTptEEUUrWUwLmF9NL37NdY+XIqUTaSU6kl6V5slyjJdeXzew3gb5kL+q/Av6mdWF1h9mqhriK9LqBFO9N3WjJdSNwCHgY+GXiuQ3aSW4Z2otaROoL9qVxqGujo5gi4E+TL2nQ8VnUShAivWp+uY0U1iAaShBm9iRL9Dm4+/lNj6iLzK/DpCYmkZ6VC4xskM4+iJWsxVRXIF4eY33zw+kuM5UIA/o0ikmkZ5lZsvVo+sb1NPTRNtnRrf61z93/APip1oaWfvUhroGW2RDpaWnderTRJqZLF9wNiGsUK9lLoifNaKtRESHuhzxcTN+uyY0W8v9jwe0q8BTwr5oeTZfRMhsiAnE/5NOV9C230egoph9vdSDdaKYSMVbItjsMEWmzgWxAseZUIycTpKfJudEmpl871Xl3v6U54XSP+jIbqkGISH0u1Ew1XXtTr2QU0+Uc3zL0zcD9wOOtCKoblGpOzTUHQkSOD3WfqXRngjgbuNTdpwDM7IPA5939F1oVWNrNT5LTEFeRnrewBpEmjX683QSUF9wvJ8fkJOpbDKoGISL1D4ppG+raaA3iz4H7zeyzyf23Are3JKIucbwGoQQh0uv65xfsS9dkuUZHMf2umf0d8Jrk0L9x92+1Lqz000J9IlIXmtGXsa5tYgLoBybd/Q+BvWZ2Xoti6gqz1YgAKITqgxCRZGe5lDUxNbrl6AeA3wDelxzKAp9sVVDdYLoSMZANMC2zISLE/ZFpW9G10RrEzwBvAWYA3H0/MNSqoLrBrOZAiMgC8YJ93Zkgyh7vuO0AZjbQupC6Q1yDUO1BRGL1BfviojQdGk0QnzGzPwFGzeyXgC+gzYNOSQv1ichCA9mAmseTaNNi2VFMFjeifxq4CJgEXgy8393vbXFsqRUly2wMqolJRBL1uRAz1YhCSsqGZROEu7uZ3e3uLweUFBowW3UcDXEVkePqLQrTlYixQpuDaVCjJdhDZnZ5SyPpIvWhbGpiEpG648ttdFETU+JVwC+Y2VPEI5mMuHJxSasCS7MZTZITkUUGFyzYlxanTBBmttXdnwHeuEbxdIVpLbMhIovkQyO0dK3HtFwJ9jkAd38auMXdn174tdwPN7OrzOwxM9tjZjcucT5vZp9Ozn/TzLYtOr/VzKbN7L2NP6X20zIbIrKYmaVuLsRyJdjCgfznr+QHm1kIfBR4E3Ax8HYzu3jRZe8Cjrr7BcCtwM2Lzt8C/N1Kfm8nmKlEFEJL1c5RItJ6aZtNvVyC8JPcbsQVwB53f8Ldy8CdwNWLrrma46vC3gW8PhlWi5m9FXgS2L3C39t205VItQcROcFANl3rMS1Xir3CzCbNbAq4JLk9aWZTZja5zGO3AM8uuL83ObbkNe5eBSaAMTMbJF776bdP9QvM7Hoz22Vmuw4dOrRMOGtnuqJlNkTkRIPd1MTk7qG7D7v7kLtnktv1+8MtjOuDwK3uPr1MfLe5+w5337Fx48YWhrMy01XVIETkRANZY7bqRClZbqPRYa6rsQ84Z8H9s5NjS12z18wywAhwhHhY7TVm9mFgFIjMrOjuH2lhvE3h7syoiUlElrBw69GhbOfvTd3KBPEAsD3ZN2IfcC3wjkXX7ASuA74OXAN8MVkUsL4xUX3/6+k0JAeAYs2puSbJiciJBubnQjhD2TYH04CWJQh3r5rZDcA9QAh83N13m9lNwC533wl8DLjDzPYA48RJJNU0xFVETmYgm67Jcq2sQeDudwN3Lzr2/gW3i8DblvkZH2xJcC0yP4tandQiski9BjGdko5qlWJNVn/hVYMQkcUGU1aDUCnWZDPzC/VpkpyIvFAmMPKhpWaoqxJEk01XIrIB5EP9aUXkRIOZ9EyWUynWZJpFLSKnkqblNlSSNdl0VbOoReTkBlO03IZKsiabqbhqECJyUoPZgKlKhKdgNrVKsiabrkSaJCciJzWUDah5PKm206kka6JyzSlHrjkQInJS9RaGqRQ0M6kka6IZzYEQkWUMJeVDGvohVJI1kZbZEJHlqAbRo6bnJ8npzyoiSxtUDaI3qQYhIsvJBEZfxpQges1MJSIw6Au1zIaInNxgJlATU6+ZrkYMZgKSbbVFRJY0lAuYLitB9BTNgRCRRqRlNrVKsybSVqMi0oihbMBMNer4valVmjXRVCWaH+MsInIyQ9kQp/P3hVBp1iTlmlOsuRKEiCwrLXMhVJo1yVSlBsBwTn9SETk1JYgeM5mMSBjKhW2OREQ63UjyQXKyw0cyKUE0yWTySWBYTUwisoxCaGQDmCzX2h3KKak0a5KpsmZRi0hjzIyhbDj/wbJTqTRrkslKjYGMkQk0SU5EljecC9TE1CumypH6H0SkYcO5YL7loVMpQTTJZCVS/4OINGw4GzJdjahGnTtZTiVaE7h7UoPQn1NEGlMfEt/JS26oRGuCUrLVqGoQItKoeoKY6OCRTCrRmmB+iKv6IESkQSNJedHJHdVKEE1Q72jSMhsi0qh6edHJQ11VojXBpJbZEJEVygRGf8Y6erKcSrQmOFaKCE2T5ERkZYZzoZqYut2xco3hXECgneREZAWGs509Wa6lCcLMrjKzx8xsj5nduMT5vJl9Ojn/TTPblhx/g5k9aGYPJ99f18o4T9dEKWJUHdQiskKj+ZBj5RreoRsHtSxBmFkIfBR4E3Ax8HYzu3jRZe8Cjrr7BcCtwM3J8cPAm9395cB1wB2tirMZjpVrjOaVIERkZdblA2reuct+t7IGcQWwx92fcPcycCdw9aJrrgZuT27fBbzezMzdv+Xu+5Pju4E+M8u3MNZVK1YjijVnVB3UIrJC9ZaHo6XO7KhuZam2BXh2wf29ybElr3H3KjABjC265meBh9y9tPgXmNn1ZrbLzHYdOnSoaYGvxLGk/XBENQgRWaF1SblxrEP7ITr6Y6+ZvZS42emXlzrv7re5+w5337Fx48a1DS5xLBmipj4IEVmp4VxAABzrwRrEPuCcBffPTo4teY2ZZYAR4Ehy/2zgs8C/dvcftjDO0zKRvLCj+Y7OtSLSgQIzhnNBTzYxPQBsN7PzzCwHXAvsXHTNTuJOaIBrgC+6u5vZKPB54EZ3/2oLYzxtx8oRhdAohEoQIrJy6/Ihx0o91sSU9CncANwDPAJ8xt13m9lNZvaW5LKPAWNmtgf4NaA+FPYG4ALg/Wb27eTrjFbFejqOlTSCSURWbzQfcrRDZ1NnWvnD3f1u4O5Fx96/4HYReNsSj/sd4HdaGVuzHCvX2NTX0j+jiHSx0VxAqebMVSP6Mp3VEtFZ0aRMzZ2JUjQ/EkFEZKXmRzJ1YD+EEsRpOFqqEQFjBSUIEVmdehP10Q7sh1CCOA1HinHGV4IQkdVanw8x4Eip2u5QTqAEcRrmE0RefRAisjqZwBjNBxwuqompqxwp1hjOBuRCreIqIqu3oZDh8JwSRFc5UqypeUlETtuGQsh4qUYt6qxVXZUgVsndOVKqKkGIyGnbUAhxYLzDRjIpQazSZCWiEqmDWkRO34ZC3I/Zaf0QShCrpA5qEWmWsUI8kulwsbNGMilBrNJhDXEVkSbp1JFMShCr9PxslaFswEBWf0IROX0bChkOddhIJpVuq/TcbJUz+9W8JCLNsakvw3ipRqnWOTOqlSBWoVSLGC/VlCBEpGk2D8TlyYHZzumHUIJYhfoLeJYShIg0Sb08eU4JIt3qCeJMLfMtIk3SlwkYzQXsn1GCSLUDs1WGcwH96qAWkSbaPJBVDSLtnputqnlJRJrurP4MU5WIqUpnjGZSglihqUqNY+WIzUoQItJk9Y7qTmlmUoJYoaenKgCcO5RrcyQi0m029WXIGDwzXWl3KIASxIo9NVWhL2Ns6tMMahFprkxgbB3K8uSkEkTquDtPTVbYNpjFTHtAiEjznT+UY7xU64g9qpUgVuBIscZ0NWLbsJqXRKQ1zk/Klycmy22ORAliRZ5M+h+2DWXbHImIdKt1+YCRXMATU+1vZlKCWIHvHy1xRl/ISE79DyLSGmbGi4ZzPD1Vbvu6TEoQDTpcrPLcbJWXrS+0OxQR6XIvXZ+nEsGjx9rbzKQE0aDd4yUMeOm6fLtDEZEut7k/w1gh5DuHi22NQwmiAZE73xsvcf5wVvs/iEjLmRmvGCuwf7bKobn2TZpTadeAh4+UmKpEvHKDmpdEZG28bF2e0OD+g3Nti0EJYhmVyPnKgVm2DGS4QMNbRWSN9GcDLtvYx8PjJZ5v0wJ+ShDLuP/gHFOViCvPGtDkOBFZU/9iUx99oXHfvhncfc1/vxLEKTw1WeYrz83yktEcWzX3QUTWWCET8GOb+3lmusJXDsyu+e/XkqQnsXe6wueemmKsEPKmrUPtDkdEetQrxwrsn6ny1QNz9GcCLt1QWLPWjJbWIMzsKjN7zMz2mNmNS5zPm9mnk/PfNLNtC869Lzn+mJm9sZVxLlSuOV87MMtf7JmgL2P87PnD5EI1LYlIe5gZV50zyIuGs9y7d4a/eXp6zdZpalkNwsxC4KPAG4C9wANmttPdv7/gsncBR939AjO7FrgZ+Dkzuxi4FngpsBn4gpld6O5N/6tUIufAbJXDxSp7p6vsmSxTqjkXjuT4ya2DFDJqhROR9goD45rzh/na83N89cAsjxwtsW0oy7ahLBsKGTb2hQy3YIWHVjYxXQHscfcnAMzsTuBqYGGCuBr4YHL7LuAjFtedrgbudPcS8KSZ7Ul+3tebHeTBuSqfenwCgL6MccFwjss2Ftg8oD4HEekcZsaPntnPy9fneehQkccnynxpf9wv8eLRHD9z3nDTf2crE8QW4NkF9/cCrzrZNe5eNbMJYCw5/o1Fj92y+BeY2fXA9cndaTN7rDmhN9UG4HC7g2giPZ/OpufTuTr1uZx7shOp7qR299uA29odx6mY2S5339HuOJpFz6ez6fl0rjQ+l1Y2sO8Dzllw/+zk2JLXmFkGGAGONPhYERFpoVYmiAeA7WZ2npnliDuddy66ZidwXXL7GuCLHs8G2Qlcm4xyOg/YDtzfwlhFRGSRljUxJX0KNwD3ACHwcXffbWY3AbvcfSfwMeCOpBN6nDiJkFz3GeIO7Srw7laMYFojHd0Etgp6Pp1Nz6dzpe65WDumb4uISOfTIH8REVmSEoSIiCxJCaKJzOzjZnbQzL634Nh6M7vXzB5Pvq9rZ4wrcZLn83tm9qiZfdfMPmtmo20McUWWej4Lzv26mbmZbWhHbCt1sudiZv8heX12m9mH2xXfSp3kvfZKM/uGmX3bzHaZ2RXtjHElzOwcM/uSmX0/eS3+U3I8VeWBEkRzfQK4atGxG4H73H07cF9yPy0+wYnP517gZe5+CfAD4H1rHdRp+AQnPh/M7BzgJ4Bn1jqg0/AJFj0XM/tx4lUIXuHuLwV+vw1xrdYnOPG1+TDw2+7+SuD9yf20qAK/7u4XAz8CvDtZQihV5YESRBO5+z8Sj8Za6Grg9uT27cBb1zKm07HU83H3/+fu9d1LvkE8RyUVTvL6ANwK/BcgNSM2TvJcfgX4ULJEDe5+cM0DW6WTPB8H6utHjAD71zSo0+Duz7n7Q8ntKeAR4tUgUlUeKEG03iZ3fy65fQDY1M5gmuzfAn/X7iBOh5ldDexz9++0O5YmuBB4TbIy8pfN7PJ2B3Sa3gP8npk9S1wbSlNtdV6ySvU/A75JysoDJYg1lEwCTM2n1FMxs/9KXI3+VLtjWS0z6wd+k7j5ohtkgPXETRr/GfiMpXsbxF8BftXdzwF+lXjeVKqY2SDwf4D3uPvkwnNpKA+UIFrveTM7CyD5nppq/8mY2TuBnwZ+3tM9keZFwHnAd8zsKeLmsofM7My2RrV6e4G/9tj9QES8QFxaXQf8dXL7r4hXdE4NM8sSJ4dPuXv9eaSqPFCCaL2Fy4lcB/zfNsZy2szsKuL2+re4+9rvgdhE7v6wu5/h7tvcfRtxAXupux9oc2ir9TngxwHM7EIgR2euHtqo/cCVye3XAY+3MZYVSWpuHwMecfdbFpxKV3ng7vpq0hfwl8BzQIW4sHkX8fLl9xG/ub8ArG93nKf5fPYQL9H+7eTrj9sd5+k8n0XnnwI2tDvO03htcsAnge8BDwGva3ecp/l8Xg08CHyHuP3+snbHuYLn82ri5qPvLvhf+cm0lQdaakNERJakJiYREVmSEoSIiCxJCUJERJakBCEiIktSghARkSUpQUhPMbNasjrobjP7TrKKa5Cc22Fmf3SKx24zs3ec4vxmM7sruf1OM/vICmN7p5ltXnD/z5IF3kTaomVbjop0qDmPVwfFzM4A/oJ4QbgPuPsuYNcpHrsNeEfymBcws4y77yfeW3213kk8h2E/gLv/4mn8LJHTphqE9CyPVzu9HrjBYq81s78FMLMrk5rGt83sW2Y2BHyIeDG8b5vZryaf+Hea2ReB+5IaxsL9Gc4xs39I1v7/QPJzX3CNmb3XzD5oZtcAO4BPJT+/L3nsjuS6t5vZw2b2PTO7ecHjp83sd5Pa0DfMrKMXf5N0UYKQnubuTwAhcMaiU+8F3p3UNl4DzBGv3f9P7v5Kd781ue5S4Bp3v5ITXQH8LHAJ8LZ6YX+SOO4irr38fPLz5+rnkmanm4mXm3glcLmZvTU5PQB8w91fAfwj8EsNPnWRZSlBiCztq8AtZvYfgVE/vgfGYve6+1J7TNTPHUkK+78mXn5hNS4H/sHdDyVxfAr4seRcGfjb5PaDxM1gIk2hBCE9zczOB2osWlXT3T8E/CLQB3zVzC46yY+YOcWPX7yOjRMvkb7w/66wooBPVPHj6+XUUL+iNJEShPQsM9sI/DHwEV+0KJmZvcjj1V5vBh4ALgKmgKEV/Io3JHsQ9xHvHPZV4HngDDMbM7M88bLpdSf7+fcDV5rZBjMLgbcDX15BHCKrok8b0mv6zOzbQJb40/wdwC1LXPeeZI/nCNhNvHNeBNTM7DvEeygfXeZ33U+8H8DZwCeTUVKY2U3JuX3Aowuu/wTwx2Y2B/zz+kF3f87MbgS+BBjweXfv7GWipStoNVcREVmSmphERGRJShAiIrIkJQgREVmSEoSIiCxJCUJERJakBCEiIktSghARkSX9f5jTDVybIH0XAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "rv = sp.stats.uniform(loc=10, scale=10)\n",
    "rvs = rv.rvs(size=100000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution ', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 정규분포 (Normal Distribution)\n",
    "\n",
    "평균값을 중심으로 대칭을 이루는 종 모양의 분포, 자연에서 일어나는 많은 수의 데이터들이 정규분포를 따르는 경우가 많기 때문에 통계학에서 \n",
    "가장 중요하게 다루는 분포입니다.\n",
    "\n",
    "**확률밀도함수**\n",
    "\n",
    "$$f(x) = \\frac{1}{\\sqrt{2\\pi\\sigma}}exp\\{-\\frac{(x-\\mu)^2}{2\\sigma^2}\\} \\quad (-\\infty < x < \\infty)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = \\mu \\quad V(X) = \\sigma^2$$\n",
    "\n",
    "**표준정규분포(Z Distribution)**\n",
    "\n",
    "표준졍규분포는 데이터의 평균값을 0으로 표준편차를 1로 변환하여 데이터의 척도에 상관 없이 사용할 수 있도록 표준화한 분포입니다. \n",
    "\n",
    "표준화변량 (Z-Score)\n",
    "\n",
    "$$Z = \\frac{x-\\mu}{\\sigma}$$\n",
    "\n",
    "표준화변량(Z-score)를 이용하면 평균과 표준편차가 다른 두 집단에 속한 데이터가 표준 정규 분포 상의 어느 확률 지점에 존재하는지 같은 기준을 통해 비교해 볼수 있게 됩니다. 예를 들면, 사내 어학연수 선발에서 토익성적만 있는 지원자와 토플성적만 있는 지원자 중 선발이 필요할 경우 직접적 비교가 어렵지만, 두 지원자의 점수를 Z-score로 표준화하여 같은 분포상에서 비교한다면 선발이 가능하게 됩니다.\n",
    "\n",
    "![](https://mathbitsnotebook.com/Algebra2/Statistics/zscore3.png)\n",
    "\n",
    "https://mathbitsnotebook.com/Algebra2/Statistics/STzScores.html\n",
    "\n",
    "**왜도와 첨도(Skew & Kurtosis)**\n",
    "\n",
    "표준분포의 모양이 정규분포에서 어느정도 벗어나는지를 측정하기 위한 지표\n",
    "\n",
    "왜도 (Skew)\n",
    "\n",
    "$$S_w = \\frac{1}{n}\\sum_{i=1}^{n}(\\frac{x_i-\\mu}{\\sigma})^3$$ \n",
    "\n",
    "첨조 (Kurtosis)\n",
    "\n",
    "$$S_k = \\frac{1}{n}\\sum_{i=1}^{n}(\\frac{x_i-\\mu}{\\sigma})^4 - 3$$ \n",
    "\n",
    "![](https://www.researchgate.net/profile/Attila-Bonyar/publication/298415862/figure/fig1/AS:340236723867648@1458130164255/Illustration-of-the-skewness-and-kurtosis-values-and-how-they-correlate-with-the-shape-of.png)\n",
    "\n",
    "https://www.researchgate.net/figure/Illustration-of-the-skewness-and-kurtosis-values-and-how-they-correlate-with-the-shape-of_fig1_298415862"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 13,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>Sepal.Length</th>\n",
       "      <th>Sepal.Width</th>\n",
       "      <th>Petal.Length</th>\n",
       "      <th>Petal.Width</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>-0.90068</td>\n",
       "      <td>1.01900</td>\n",
       "      <td>-1.34023</td>\n",
       "      <td>-1.31544</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>-1.14302</td>\n",
       "      <td>-0.13198</td>\n",
       "      <td>-1.34023</td>\n",
       "      <td>-1.31544</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>-1.38535</td>\n",
       "      <td>0.32841</td>\n",
       "      <td>-1.39706</td>\n",
       "      <td>-1.31544</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>-1.50652</td>\n",
       "      <td>0.09822</td>\n",
       "      <td>-1.28339</td>\n",
       "      <td>-1.31544</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>5</th>\n",
       "      <td>-1.02185</td>\n",
       "      <td>1.24920</td>\n",
       "      <td>-1.34023</td>\n",
       "      <td>-1.31544</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   Sepal.Length  Sepal.Width  Petal.Length  Petal.Width\n",
       "1      -0.90068      1.01900      -1.34023     -1.31544\n",
       "2      -1.14302     -0.13198      -1.34023     -1.31544\n",
       "3      -1.38535      0.32841      -1.39706     -1.31544\n",
       "4      -1.50652      0.09822      -1.28339     -1.31544\n",
       "5      -1.02185      1.24920      -1.34023     -1.31544"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/plain": [
       "Sepal.Length    0.31491\n",
       "Sepal.Width     0.31897\n",
       "Petal.Length   -0.27488\n",
       "Petal.Width    -0.10297\n",
       "dtype: float64"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/plain": [
       "Sepal.Length   -0.55206\n",
       "Sepal.Width     0.22825\n",
       "Petal.Length   -1.40210\n",
       "Petal.Width    -1.34060\n",
       "dtype: float64"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Scipy 를 이용한 각 변수의 Z-score 계산\n",
    "#sp.stats.zscore(df_iris['Sepal.Length'])\n",
    "\n",
    "# Pandas에서 apply()에 zscore()를 전달하여 계산\n",
    "df_zscore = df_iris.drop('Species', axis=1).apply(sp.stats.zscore)\n",
    "display(df_zscore.head())\n",
    "\n",
    "# Pandas에서 Skew / Kurtosis 계산\n",
    "display(df_iris.skew())\n",
    "display(df_iris.kurtosis())"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 14,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "f(82)=0.071\n",
      "F(82)=0.650\n",
      "1 - F(82)=0.350\n",
      "E(X)=80.000, V(X)=27.040\n",
      "Top 10% point with ppf: 86.664\n",
      "Top 10% point with isf: 86.664\n",
      "중위 90% interval: 71.447 < x < 88.553\n",
      "상하위 5% interval with ppf: x < 71.447, 88.553 < x\n",
      "상하위 5% interval with isf: x < 71.447, 88.553 < x\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 14,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEGCAYAAAB/+QKOAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAuwUlEQVR4nO3deXSd9Xng8e9z9yvpXsnabLxKXjAxi40jICEhG00HmhYnLTTQtCU9tDSn4XQymZwZ2jNDU850TpkzE6adZNoypS0hTYDSJnESGpqGbCUBbMAsNtjI8iJ5lbVdbXd/5o/3FVzkK/vK0qu7PZ9zdHTv+7736uFF8nN/2/MTVcUYY4yZzVfuAIwxxlQmSxDGGGOKsgRhjDGmKEsQxhhjirIEYYwxpqhAuQNYLO3t7drV1VXuMIwxpqo8//zzZ1S1o9i5mkkQXV1d7N69u9xhGGNMVRGRI3Odsy4mY4wxRVmCMMYYU5QlCGOMMUVZgjDGGFOUJQhjjDFFWYIwxhhTlCUIY4wxRVmCMGaRqSpWRt/UgppZKGdMuSWzeZ45Pc3LQ0lSOaU17Of61Y10xULlDs2YC2ItCGMWwenpLH+3f5RnT02zqjFIT0eUnMIjvQmePTVV7vCMuSDWgjBmgU5MZXjkjQRBn/DrFzezqjEIwHtWNPCdo+P84PgUy6MBuuLWkjDVxVoQxizA6eksj/YmiASE39z8VnIACPmFj6yN0Rbx860j40xl8mWM1Jj5swRhzAUaSmZ5pHeMoE+4bWMz8ZD/rGtCfmFHV4yprPJT62oyVcYShDEXYDSV45HeBAC3bozTEj47OczojAa4vC3Mi2eSjKVzSxWiMQtmCcKYeUqkc3ytd4xMXrl1YzNtkfMP5b13RQMAT5+wVoSpHpYgjJmH4WSOrxwYYzqrfHxDnM5oafM84iE/W9si7B1JMWljEaZKWIIwpkSHx9M8/MYoWVV+bVMzFxUMSJdiZurri2eSHkVozOKyBGHMeagqz56a4tHeBA0BH7++qYUVDfOfId4a8bMhHuTFM9Nk87bS2lQ+TxOEiNwgIvtFpFdE7i5yPiwij7rnnxWRLvf4J0RkT8FXXkS2eRmrMcWkc8o3DjtrGTa3hLj94hZaI3MPSJ9PT0eUyayyfzS1iFEa4w3PEoSI+IEvATcCW4DbRGTLrMvuAEZUdSNwP3AfgKr+vapuU9VtwG8Ah1R1j1exGlPMSCrHlw+McmA0zQdXNrCjK0bILwt6z65YkOaQj5eGLEGYyudlC+JqoFdV+1Q1DTwC7Jh1zQ7gIffx48D1IjL7L/A297XGLJlDiTQP7R9lIpPn4xviXLO8gbN/NedPRNjaFuHoRIaRlE15NZXNywSxCugveD7gHit6japmgTGgbdY1Hwe+5lGMxpxl73CSxw4miAV9fHJzy6KXyLi8NYwALw/ZYLWpbBU9SC0i1wBTqvrqHOfvFJHdIrJ7cHBwiaMztejV4STfOjLBmqYgv3FxyzkXwF2oWMjP+niQV4ZS5K0suKlgXiaIY8Caguer3WNFrxGRANAMDBWcv5VztB5U9QFV7VHVno6OjkUJ2tSvvkSa7xyZYF1TkFs2xBc83nAuW9siTGTzHEykPfsZxiyUlwliF7BJRLpFJITzj/3OWdfsBG53H98MPKXuTisi4gN+FRt/MEtgcDrL1w8l6Ij6+eX1MYI+75IDwIbmEI0BscFqU9E8SxDumMJdwJPAa8BjqrpXRO4VkZvcyx4E2kSkF/gsUDgV9n1Av6r2eRWjMQCpXJ6vHxon5BNu2RAn7Pe+59UvwuWtEQ6OpRnP2GC1qUye7gehqk8AT8w6dk/B4yRwyxyv/SHwLi/jMwbgyf5JRlI5btvUTCy4+GMOc7miLcIzp6d5dSjFu91aTcZUkooepDbGa6+PpNg3kuK9FzWwtml+pTMWqjXiZ01TgJeGkraHtalIliBM3ZrK5HlyYIIV0QDvXh4tSwxb2yKMpvMcnciU5ecbcy6WIEzd+vGJKVJZ5SPrmvAtwiK4C7G5JUzYL7xsg9WmAlmCMHXp5FSWPUNJtndE6CixZLcXgj7h0mVhXh9NkcxaGXBTWSxBmLr01LFJogF5cyOfcrqiLUJOYe+ItSJMZbEEYerO0fEMRycyXLu8gUig/H8CKxoCLI/62XPGBqtNZSn/X4cxS+zpk1M0BoRt7ZFyh/KmrW0RBpM5Tk5nyx2KMW+yBGHqysBEhiMTGa5Z3uD5aun52LIsTEDgpTPWzWQqhyUIU1eeH5wm7Be2tVVO6wEgEvBxybIwr42kSOesm8lUBksQpm5MZPLsH01zeWvY00J8F2prW4RU3nabM5XDEoSpG3vOJMkD29vLsyjufFY3BmgN+3nJ9okwFcIShKkLqspLQ0m6YsEF7SntJWe3uTADk1lOTdlgtSk/SxCmLvRPZBnP5LmitbLGHmbb2hYh6INdg9PlDsUYSxCmPuwdSRL0wcbmxd0+dLFFAj4ub42wbyTFRMZWVpvysgRhal42r7w+mubi5socnJ7tqs4oeYUXrBVhyswShKl5h8bTpHLKpa3hcodSkmVhPxubQ7w4lCSTtymvpnwsQZiad2A0TdgvrIst7X4PC3FVR4TprLJ32Ka8mvKxBGFqWl6V3kSajfEQ/jKV9L4Qa5uCdEb97B6ctvpMpmwsQZiadmwyy3RWK35wejYR4aqOKGeSOQ6N22ZCpjw8TRAicoOI7BeRXhG5u8j5sIg86p5/VkS6Cs5dISI/E5G9IvKKiFT2/ERTkXrH0vgE1serp3tpxpZlYRoDwq7TNlhtysOzBCEifuBLwI3AFuA2Edky67I7gBFV3QjcD9znvjYAfAX4lKpeCnwAsI9RZt7eGEuzrilI2F99jWW/T9jeEeXQeIYzVuXVlIGXfzVXA72q2qeqaeARYMesa3YAD7mPHweuFxEBfh54WVVfAlDVIVXNeRirqUFj6RzDqRzr49XVvVToyvYIAbGFc6Y8vEwQq4D+gucD7rGi16hqFhgD2oCLARWRJ0XkBRH5T8V+gIjcKSK7RWT34ODgov8HmOp2OOE0OruraPbSbA0BH5e2htk7nGLKtiQ1S6xS290B4L3AJ9zvHxOR62dfpKoPqGqPqvZ0dHQsdYymwh0aT9MU9NFWobWXSnVVR5SswotnrIifWVpeJohjwJqC56vdY0WvcccdmoEhnNbGj1X1jKpOAU8A2z2M1dSYvCqHxzN0x4JIFU1vLaY9GqA7FuSFwWmytnDOLCEvE8QuYJOIdItICLgV2Dnrmp3A7e7jm4Gn1Jn0/SRwuYg0uInj/cA+D2M1NebUdJZkTumq4u6lQld1RpnMKq+N2MI5s3Q8SxDumMJdOP/YvwY8pqp7ReReEbnJvexBoE1EeoHPAne7rx0BvoCTZPYAL6jqd7yK1dSeI+7aga5Y9Q5QF+qOBWmP+NllC+fMEgp4+eaq+gRO91DhsXsKHieBW+Z47VdwproaM2/9Exnawn4ag5U6zDY/IkJPR5Tv9k9wdCLDuhpJfKay1cZfjzEFVJVjk1lWN3n6+WfJXdoaJhoQdg3aYLVZGpYgTM05k8yRzCmrG2tj/GFG0Cdc2RahdyzNSMqWBRnvWYIwNWdg0hl/WN1UWwkCYHtHFJ9g5TfMkrAEYWrOwESWxoDQEqq9X++moI8ty8K8MpwkaQvnjMdq7y/I1L2ByQyrm6p//cNc3tkRIZOHvTbl1XjMEoSpKYl0jrF0vubGHwqtiAZYHvXz0lDSprwaT1mCMDXl2KRT9XRNDY4/zBARtrZFOD2d4+SUVXk13rEEYWpK/0SGoA86o9Vdf+l8trSGCfpgz5BNeTXesQRhasrAZIZVjUF8NTr+MCPi93FJS5jXRtKkcjZYbbxhCcLUjGQuz+B0rqbHHwpta4+QziuvjaTLHYqpUZYgTM04PplFoeZWUM9lZUOAjogzWG2MFyxBmJoxMJFBgJUN9dGCmBmsPjGV5bRtSWo8YAnC1IyBySzLGwKE/LU9/lBoS2sYH7Bv2NZEmMVnCcLUhFxeOT6ZYXVjfXQvzWgI+OiOB9k3krI1EWbRWYIwNeHUdJas1mb9pfPZsixMIpOnf9K6mczisgRhakL/hFugr05mMBXa1OysibBuJrPYLEGYmjAwmWVZ2EdTjWwQNB8hv7AxHuLAWIq8dTOZRVR/f02m5qiqU6CvDlsPMy5uCTOV1TdLjRizGCxBmKo3nMoxndW6HH+YsT4exC9wYNS6mczi8TRBiMgNIrJfRHpF5O4i58Mi8qh7/lkR6XKPd4nItIjscb/+0ss4TXUbcD8119sMpkJhv491sSBvjKVtNpNZNJ4lCBHxA18CbgS2ALeJyJZZl90BjKjqRuB+4L6CcwdVdZv79Smv4jTVb2AiQzQgtIZru0Df+VzcHGY0nWcwaduRmsXhZQviaqBXVftUNQ08AuyYdc0O4CH38ePA9VKru7wYz8yMP9T7r86m5hAAB0atNpNZHF4miFVAf8HzAfdY0WtUNQuMAW3uuW4ReVFEfiQi1xX7ASJyp4jsFpHdg4ODixu9qQoTmTwjqXxddy/NaAz6WN0Y4MCYjUOYxVGpg9QngLWqeiXwWeCrIhKffZGqPqCqPara09HRseRBmvIbmHTWP9TyBkHzsak5xOnpHKMp62YyC+dlgjgGrCl4vto9VvQaEQkAzcCQqqZUdQhAVZ8HDgIXexirqVIDExkCAsuj1oIAZ7orwIEx62YyC+dlgtgFbBKRbhEJAbcCO2ddsxO43X18M/CUqqqIdLiD3IjIemAT0OdhrKZKDUxmWdkYxO+r7/GHGcvCfjoift6wbiazCDxLEO6Ywl3Ak8BrwGOquldE7hWRm9zLHgTaRKQXpytpZirs+4CXRWQPzuD1p1R12KtYTXVK55RTU1kbf5hlY3OIYxNZkrbTnFkgT/+yVPUJ4IlZx+4peJwEbinyun8E/tHL2Ez1Oz6VcTcIsvGHQt3xED87Nc2R8Qyb3S4nYy5EpQ5SG3NeAxNZBFhlLYi3WdUYIOwT+hI2DmEWpqQEISKXex2IMfM1MJmhI+on7LfPOYX8IqyLBTmUyNiqarMgpf5l/V8ReU5Efk9Emj2NyJgS5FU5VucF+s5lfTxEIpNnyFZVmwUoKUGo6nXAJ3CmpD4vIl8VkQ97Gpkx53ByKksmb+sf5rI+7tyXg9bNZBag5La5qr4B/BfgPwPvB/5cRF4XkV/2Kjhj5nLU3SBorSWIouIhP+0RP4fGM+UOxVSxUscgrhCR+3Gmq34I+CVVfYf7+H4P4zOmqCPjGdojfhrrcIOgUq2Ph+ifyJDO2TiEuTCl/nX9H+AFYKuqflpVXwBQ1eM4rQpjlkzO3SDIWg/ntj4WJKdvtbaMma9S5wd+BJhW1RyAiPiAiKpOqerDnkVnTBEnJp3xh7UxSxDnsropSNAHfYk0G91Kr8bMR6ktiH8FogXPG9xjxiw5G38oTcAnrG0K0pewTYTMhSk1QURUdWLmifu4wZuQjDm3I+MZOiJ+GgI2/nA+6+MhRtNOSXRj5qvUv7BJEdk+80RE3glMexOSMXPL5p31D+use6kkG+JO11LfuE13NfNX6hjEZ4B/EJHjgAArgI97FZQxczkxlSWr1r1Uqpawn2VhH32JND0d0fO/wJgCJSUIVd0lIpcAm91D+1XVpkaYJXdk3MYf5mt9PMRLZ5Jk8krQyqKbeZhPJ+5VwBXAduA2EflNb0IyZm5HJzIsj/qJ2PhDydbHQmQV+m26q5mnkloQIvIwsAHYA8wUd1Hgy96EZczZZsYf3mldJfOyNhbEL3AokWZ93Ka7mtKVOgbRA2xRmytnyqh/IkNOYZ11L81LcGa663iG68sdjKkqpbbTX8UZmDambA4m0gTEFshdiO54iKFkjrG0VXc1pSu1BdEO7BOR54A3N7tV1Zvmfokxi6sv4ZTXsIHW+VsfC/IUcCiRYVu7v9zhmCpRaoL4vJdBGHM+I6kcw6kc2zsi5Q6lKrVF/MSDznTXbe12D01pSt0P4kfAYSDoPt6FU7zvnETkBhHZLyK9InJ3kfNhEXnUPf+siHTNOr9WRCZE5HOlxGlq18z2mRtskPWCiAjd8SBHxjPkbCjRlKjUct+/AzwO/JV7aBXwjfO8xg98CbgR2IIzNXbLrMvuAEZUdSNO2fD7Zp3/AvDPpcRoatvBRJplYR/LwtY9cqHWx0Ok8srxyWy5QzFVotRB6k8D7wES8ObmQZ3nec3VQK+q9qlqGngE2DHrmh3AQ+7jx4HrRUQAROSjwCFgb4kxmhqVyStHxzM2RXOB1sWCCG+1xow5n1ITRMr9Rx4AEQngrIM4l1VAf8HzAfdY0WtUNQuMAW0i0oSzc90fn+sHiMidIrJbRHYPDg6W9B9iqs/R8QxZte6lhYr4faxqDHAoYQvmTGlKTRA/EpE/BKLuXtT/AHzLu7D4PHB/YQXZYlT1AVXtUdWejo4OD8Mx5fTm9FZb/7Bg6+MhTk5nmcxYdVdzfqUmiLuBQeAV4HeBJzj/TnLHgDUFz1e7x4pe47ZKmoEh4Brgf4jIYZxCgX8oIneVGKupIapKXyLNuliQgE1vXbCZbrpDVt3VlKDUYn154P+5X6XaBWwSkW6cRHAr8GuzrtkJ3A78DLgZeMpdrX3dzAUi8nlgQlW/OI+fbWrEcCrHaDrP1Z1WXmMxLI/6aQgIhxIZLmu16a7m3EqtxXSIImMOqrp+rteoatb91P8k4Af+RlX3isi9wG5V3Qk8CDwsIr3AME4SMeZN+0fd6a22ZeaiEBG6YyH6xp1d5tw5IcYUNZ9aTDMiwC1A6/lepKpP4HRHFR67p+Bx0n2vc73H50uM0dSg/aMpVjYEaA7Z9NbFsj4eZO9IilPTOVY0lPpPgKlHpS6UGyr4Oqaq/xv4iLehmXo3mspxajrH5hZrPSymrpi7y5xNdzXnUWoX0/aCpz6cFoV99DCe2j/qlP3a3BIucyS1pTHoY0U0QF8izbUrbGt5M7dS/5H/XwWPszhlN3510aMxpsDro2lWRAO02OrpRbc+HuRnp6ZJZvO2+ZKZU6mzmD7odSDGFBpL5zgxleX9F9knXC90x0P89NQ0hycyXGItNDOHUruYPnuu86r6hcUJxxjHAXf2knUveWNVY4CwXziUSFuCMHOazyymq3DWLQD8EvAc8IYXQRmzfzRFR8RPa8S6l7zgE6ErFuRQImPTXc2cSk0Qq4HtqjoOby5e+46q/rpXgZn6NZ7OMTCZ5TrrXvJUdyzE/tE0Q8kc7VGbc2LOVuro1HKgcE5c2j1mzKI7MDbTvWTTW73UHXdqW/WNW/E+U1ypHxu+DDwnIl93n3+Ut8p0G7Oo9o+maYv4aY/Yp1ovNYf8tEf89CXSVsrEFFXqQrk/AX4LGHG/fktV/7uXgZn6NJnJ0z+RsdbDEumOBemfyJDJ2y5z5mzzmQDdACRU9c+AAbcInzGL6sBYCgWbWbNE1sdD5NTZc8OY2UrdcvSPcDbw+QP3UBD4ildBmfq1f9TZWrTDZi8tiTVNQQICfVb+2xRRagviY8BNwCSAqh4HYl4FZerTdDbPkXFn4ZZNu1waAZ+w1p3uasxspSaItLtPgwKISKN3IZl6dWAsjWKL45ba+ljI2XcjlSt3KKbClJogHhORvwJaROR3gH9lfpsHGXNe+0dTNId8LI9a99JSsl3mzFzOO49QnLb+o8AlQALYDNyjqt/zODZTR5LZPIfHM/R0RK17aYktC/toDvnoS2S4st2mu5q3nDdBqKqKyBOqejlgScF44o2xNHmFS2x665ITEdbHQ+wdTpHLK37b+9u4Su1iekFErvI0ElPX9o+miQd9XGQ7nJXF+niQdF4ZmLTBavOWUhPENcAzInJQRF4WkVdE5OXzvUhEbhCR/SLSKyJ3FzkfFpFH3fPPikiXe/xqEdnjfr0kIh+b13+VqSqpXJ5D42kubglZ91KZrG0K4hPos9lMpsA5P66JyFpVPQr8u/m+sYj4gS8BHwYGgF0islNV9xVcdgcwoqobReRW4D7g48CrQI+qZkXkIuAlEfmWqmbnG4epfAfHMuTUZi+VU9jvY01jkIOJNB9cZZMUjeN8LYhvAKjqEeALqnqk8Os8r70a6FXVPlVNA48AO2Zds4O3ajo9DlwvIqKqUwXJIII7vdbUptdHUzQFfKxutO6lctrYHOJM0qa7mrecL0EUtvfXz/O9VwH9Bc8H3GNFr3ETwhjQBiAi14jIXuAV4FPWeqhN6ZzSl7DupUqwqdmZIPDGmE13NY7zJQid47HnVPVZVb0UZ6OiPxCRyOxrROROEdktIrsHBweXMjyzSPoSabJqpb0rQUvYqe7aawnCuM6XILaKSEJExoEr3McJERkXkcR5XnsMWFPwfLV7rOg1IhIAmoGhwgtU9TVgArhs9g9Q1QdUtUdVezo6Os4TjqlE+0dTNASENU3BcodigI3xEP0TGZK5fLlDMRXgnAlCVf2qGlfVmKoG3Mczz+Pnee9dwCYR6RaREHArb21ZOmMncLv7+GbgKXfdRbebMBCRdTiL9A7P87/NVLhMXulNpLm4OYzPupcqwsbmEHmw2kwGKH3DoHlzZyDdBTwJ+IG/UdW9InIvsFtVdwIPAg+LSC8wjJNEAN4L3C0iGSAP/J6qnvEqVlMehxJpMnnrXqokKxsDRANC71iadyyzWWX1ztNpI6r6BPDErGP3FDxOArcUed3DwMNexmbKb/9omojfqSZqKoNPhA3xEL1jafKq1rKrc/PZMMiYRZPNK71jaS5uDuG3f4QqysZ4iGROOTZpEwfrnSUIUxaHxzOk8mqL4ypQd9xZVW3TXY0lCFMW+0dThP1Cl3UvVZyw30dXU5D9oymcbWBMvbIEYZZcNq8cGEuzMR6yyqEV6pJlYcbSeU5OWzdTPbMEYZbcofE0qZyyxWbJVKxNzSF8wOsj1s1UzyxBmCW3bzhF1C90xa17qVJFAz66YkFet26mumYJwiypdE55YyzNJcvCNnupws10Mx2fsm6memUJwiypN8ZSZBXrXqoCm1tCBAT2DqfKHYopE0sQZkntG0kRD1pp72oQ9vu4uCXMvpEU2bx1M9UjSxBmyUxl8xxKZHjHsrCV9q4Sl7WGSeaUgwkbrK5HliDMktk/miKPdS9Vk65YkMaA8PJQstyhmDKwBGGWzL6RFG0RP51Rf7lDMSXyibC1LcLBRIaxtO00V28sQZglMZLK0T+RZYt1L1Wdre0RBNhzxloR9cYShFkSe84kEeCKVuteqjbNIT8b4iFeGkqSs8HqumIJwngul1deGU6ysTlELGTdS9Voe0eEqayyb8SmvNYTSxDGcwfG0kxllW1tZ20rbqpEdyxIR8TPc6enbWV1HbEEYTy350ySeMhHt5XWqFoiwtWdUQaTOfpsO9K6YQnCeGo4mePIRIatbRHbnazKbVkWJhb08dNTU9aKqBOWIIynXhpyB6fbbHC62vl9wrUrohybzNJrC+fqgqcJQkRuEJH9ItIrIncXOR8WkUfd88+KSJd7/MMi8ryIvOJ+/5CXcRpvZPPKy8NJNjWHiAVtcLoWXNEWYVnYx4+PT5G3VkTN8yxBiIgf+BJwI7AFuE1Etsy67A5gRFU3AvcD97nHzwC/pKqXA7cDD3sVp/HO3uEU01lle7sNTtcKvwjvu6iRwWTOivjVAS9bEFcDvarap6pp4BFgx6xrdgAPuY8fB64XEVHVF1X1uHt8LxAVEeujqCKqynOnp+mM+lln24rWlEtaQqyIBvjJySkr4lfjvEwQq4D+gucD7rGi16hqFhgD2mZd8yvAC6p61scVEblTRHaLyO7BwcFFC9ws3MFEhqFUjms6o7ZyusaICO9f2UAinedFW11d0yp6kFpELsXpdvrdYudV9QFV7VHVno6OjqUNzpzTs6eniAd9XGKF+WpSdzxEVyzI0yenmM7myx2O8YiXCeIYsKbg+Wr3WNFrRCQANAND7vPVwNeB31TVgx7GaRbZickM/RNZejqjtmtcDfvQqkZSOeXpk1PlDsV4xMsEsQvYJCLdIhICbgV2zrpmJ84gNMDNwFOqqiLSAnwHuFtVn/YwRuOB505PE/YJW21qa03rjAbY2hbhhcEkQ0nblrQWeZYg3DGFu4AngdeAx1R1r4jcKyI3uZc9CLSJSC/wWWBmKuxdwEbgHhHZ4351ehWrWTyjqRyvj6bZ1h4h7K/oHkyzCK67qIGgT/j+sclyh2I84Om+j6r6BPDErGP3FDxOArcUed1/A/6bl7EZb+wenEaAd3bY1NZ60Bj0ce2KKD84PsXBsTQbmkPlDsksIvuIZxZNMpvnpaEk71gWJm5VW+tGT0eUZWEfTx2bJGeL52qKJQizaF48kySTh2uWR8sdillCfp/woVWNDKVyvDho015riSUIsyiyeWX34DTdsSCdUU97Lk0F2uhOe/03m/ZaUyxBmEWxbyTFZFa5utNaD/VIRLjenfb6kxM27bVWWIIwCzZTVqMj4qfLymrUrY5ogG3tEV48k2Rw2qa91gJLEGbB+hIZziRzXLPcymrUu+suaiDkF56yaa81wRKEWbDnTk8TC/p4R4stjKt3DQEf1y6Pcmg8Q/+E7TxX7SxBmAU5OZXlyESGno4Ifp+1Hgxs74jSGBD+zcYiqp4lCLMgz52eJuQTttqeD8YV9AnXLG/gyESGo9aKqGqWIMwFG0vneG0kxbb2CBErq2EKXNkesVZEDbC/anPBdp92ymr0WFkNM0vQJ7xreQNHJzIcGbf9q6uVJQhzQZyyGikrq2HmtK09QlPQx79ZOfCqZQnCXJDnzyRJ521hnJmb04qI0j+RtbGIKmUJwsxbKpdn1+lpNjaHWN5gZTXM3La2OWMRP7VWRFWyBGHm7fnBJMmc8t4VDeUOxVS4oE+4ujPK4fEMxyetFVFtLEGYeUnl8jx3epoN8SArrPVgSnBle5SIX/jpyelyh2LmyRKEmZcXzzith/dY68GUKOQXruqM0ptIc2rKajRVE0sQpmTpnFOUrzsWZGWjFeUzpXtne4SwT/jZKRuLqCaWIEzJdg9OM5W11oOZv0jAxzs7Irw+muZM0loR1cLTBCEiN4jIfhHpFZG7i5wPi8ij7vlnRaTLPd4mIj8QkQkR+aKXMZrSTGbyPHNqmoubQ6xustaDmb+ezihBH/zMxiKqhmcJQkT8wJeAG4EtwG0ismXWZXcAI6q6EbgfuM89ngT+K/A5r+Iz8/OTE1Nk88oHVjaWOxRTpRoCPra1Rdg3kmIklSt3OKYEXrYgrgZ6VbVPVdPAI8COWdfsAB5yHz8OXC8ioqqTqvpvOInClNmJqQx7hpJs74jQGrFV0+bCXbO8AZ9g6yKqhJcJYhXQX/B8wD1W9BpVzQJjQFupP0BE7hSR3SKye3BwcIHhmmLyqjzZP0ljQHjvRTb2YBamKehje3uEV4dTNhZRBap6kFpVH1DVHlXt6ejoKHc4NemFwSQnp7J8aFWjVWw1i+LdyxsI+sT2rq4CXv7FHwPWFDxf7R4reo2IBIBmYMjDmMw8jKRy/PD4JBviQbYss93izOJoCPq4ujPK/tE0A1ajqaJ5mSB2AZtEpFtEQsCtwM5Z1+wEbncf3ww8parqYUymRHlVvnNkHL9PuGFNk+01bRbV1Z1RYkEf/3psEvuTr1yeJQh3TOEu4EngNeAxVd0rIveKyE3uZQ8CbSLSC3wWeHMqrIgcBr4AfFJEBorMgDIe+vGJKQYms/z86kZiVs7bLLKQX/jAygZOTmV5eThV7nDMHDwtpqOqTwBPzDp2T8HjJHDLHK/t8jI2M7fesTTPnJpmW1uES1ttMyDjjS3Lwrx4JskPjk2yMR6iMWhjXJXG/o+YtxlL5/j2kXE6o36uX21rHox3RIQb1zaRySv/MjBR7nBMEZYgzJuyeeWbh8bJK3y0K07QZ+MOxlttkQDvWdHA/tE0rw7bsqdKYwnCAKCqfPvIOMensnxkXZMtiDNL5l3Lo6xpCvBk/wRDtjaioliCMAD86PgUr4+m+eDKBja32JRWs3R8Ity0LkbAJ/xT3zjJbL7cIRmXJQjDnjNJnjk9zZXtEdtj2pRFLOTnY11xRtI5vn5onFzepr5WAksQdW7vcJIn+ydYHw/y4dWNtt7BlM3aWJAb1zRxZCLDNw+Pk7P1EWVnCaKO7RtO8e0jE6xuCvDRrjg+Sw6mzC5vi/Bzqxo5MJbmm4fGyVpLoqwsQdSpfSMpvnVknNVNAW5Z30zIb8nBVIaezuibSeLRg2NM2ZhE2ViCqDOqzrahOw9bcjCVq6czyk1dMY5PZvnb10fpt5pNZWEJoo7k8sp3+yd46tgkm1tClhxMRduyLMxvXNxCwAdffWOMn52cIm/jEkvK01IbpnIk0jm+dWSc/oks1y6Pct1FDTYgbSreioYAn9zcwnePTvCjE1PsH0vz86sbWdlo294uBUsQNU5VeWU4xfcHJsmj/NK6JquvZKpK2O/jpq4Ym0bSPHVski8fGGNrW5jrLmqkyeo3ecoSRA07k8zyg2OTHExkWNMU4BfWxlgWthXSpvqICFtaw2xoDvL0yWl2n55m73CKbe0R3rW8wRKFRyxB1KCRVI6nT06xdzhF0Cdcv6qRno6IdSmZqhf2+/jQqkaubI/w05NTPD+YZM+ZJJe1RujpjNAesX/SFpPdzRqRyyu9iTQvDyXpS2TwC1zVGeVdnVEa7NOVqTHLwn4+si7GtSsaeObUFK8MJ9kzlKQ7FuSqzijdsaB9IFoEliCqWCKd4/B4hsPjGQ4l0kznlKagj2uWR+npiFqz29S8ZWE/N66N8f6LGtkzlOSFwSSPHUzQGvaztS3MZa0R22diASxBVJFkNs/RicybSWE4lQOgMSCsj4fYsixMdzxoK6JN3WkI+rh2RQPXdEZ5bTTFnjNJfnB8ih8dn2JDc4jNLSE2xkNEApYs5sMSRAXL5pVjkxmOuAnhxFQWBYI+WNsU5Mr2CF2xIO0RvzWnjQH8PuGy1giXtUY4k8zy8lCKfSMp3hhL48Op97S2KciqxgArG4O258l5WIKoIKrKqekcR8bTHB7P0D+RIasgwMrGANeuiNIVC7GyIYDffrGNOaf2SIAPrQrwwZUNHJ/KcmA0zcFEmh+fmAKcv6uWsI/WsJ/WsJ94yE9T0Pe2r3pPIJ4mCBG5AfgzwA/8tar+6azzYeDLwDuBIeDjqnrYPfcHwB1ADvh9VX3Sy1jLYSqb5/R0luOTWY5PZTk2kWE656wUbY/42eq2ENY2BQn7rWlszIUQEVY1BlnVGOSDqxqZzuY5Npnl+FSG4WSOoWSOI+POh7HZwn4hFvQRC/qIh3zEgn5iIR/xgue1XI3AswQhIn7gS8CHgQFgl4jsVNV9BZfdAYyo6kYRuRW4D/i4iGwBbgUuBVYC/yoiF6tqzqt4Z1NVFFCFvPtdUfc75NTpAsqpks3jfFdnNtHbzrnHUjllMptnMpMnkckzlMyRzL31G9ka9rOhOURXLMi6WJBY0NYrGOOFaMDHxuYQG5tDbx5TVZI5ZSKTf9vXeMHX6bE0k0WySMRNIvGQj3jIT0NACPt9RPxCxC+E/YJfBL84myP5BPzud584LRkRcb/z9u9IwTVvXbtUvGxBXA30qmofgIg8AuwAChPEDuDz7uPHgS+K81+/A3hEVVPAIRHpdd/vZ4sd5MmpLH//xuisROCNkE9oDAqxoJ9LWsK0Rvx0RPxc1BCwwTNjykhEiAaEaMBHxzn2zMrllXH3Q954Okci7SSPRDpPIpPj+GT2zV4AT+PlrYThE9jcEuYX18UW/ed4mSBWAf0FzweAa+a6RlWzIjIGtLnHn5n12lWzf4CI3Anc6T6dEJH9ixN6Ue3AGQ/fvxrZPTmb3ZOz2T05WyXdk3VznajqQWpVfQB4YCl+lojsVtWepfhZ1cLuydnsnpzN7snZquWeeNmvcQxYU/B8tXus6DUiEgCacQarS3mtMcYYD3mZIHYBm0SkW0RCOIPOO2ddsxO43X18M/CUqqp7/FYRCYtIN7AJeM7DWI0xxsziWReTO6ZwF/AkzjTXv1HVvSJyL7BbVXcCDwIPu4PQwzhJBPe6x3AGtLPAp5dyBtMclqQrq8rYPTmb3ZOz2T05W1XcE1HbockYY0wRNrfSGGNMUZYgjDHGFGUJYg4i0iIij4vI6yLymoi8W0RaReR7IvKG+31ZueNcKiKyWUT2FHwlROQzdX5P/oOI7BWRV0XkayIScSdlPCsivSLyqDtBo26IyL9378deEfmMe6yufkdE5G9E5LSIvFpwrOg9EMefu78vL4vI9vJFfjZLEHP7M+C7qnoJsBV4Dbgb+L6qbgK+7z6vC6q6X1W3qeo2nNpZU8DXqdN7IiKrgN8HelT1MpyJGDPlYu5X1Y3ACE45mbogIpcBv4NT9WAr8IsispH6+x35O+CGWcfmugc34szS3ISz6PcvlijGkliCKEJEmoH34cyyQlXTqjqKUwLkIfeyh4CPliO+CnA9cFBVj1Df9yQARN01PA3ACeBDOGVjoP7uxzuAZ1V1SlWzwI+AX6bOfkdU9cc4szILzXUPdgBfVsczQIuIXLQkgZbAEkRx3cAg8Lci8qKI/LWINALLVfWEe81JYHnZIiyvW4GvuY/r8p6o6jHgfwJHcRLDGPA8MOr+4whzlIipYa8C14lIm4g0AL+As+C1Ln9HZpnrHhQrSVQxvzOWIIoLANuBv1DVK4FJZjWL3QV9dTdH2O1Tvwn4h9nn6umeuH3IO3A+TKwEGjm7W6GuqOprOF1s/wJ8F9iDU66/8Jq6+R2ZSzXdA0sQxQ0AA6r6rPv8cZyEcWqm+ed+P12m+MrpRuAFVT3lPq/Xe/JzwCFVHVTVDPBPwHtwughmFqDWXYkYVX1QVd+pqu/DGYM5QP3+jhSa6x5UdFkhSxBFqOpJoF9ENruHrsdZ1V1YGuR24JtlCK/cbuOt7iWo33tyFHiXiDS4Jepnfkd+gFM2BurrfgAgIp3u97U44w9fpX5/RwrNdQ92Ar/pzmZ6FzBW0BVVdraSeg4isg34ayAE9AG/hZNQHwPWAkeAX1XV2YNRNcsdhzkKrFfVMfdYG3V6T0Tkj4GP45SDeRH4bZz+40eAVvfYr7v7mtQFEfkJTsn+DPBZVf1+vf2OiMjXgA/glPQ+BfwR8A2K3AP3w8UXcbonp4DfUtXdZQi7KEsQxhhjirIuJmOMMUVZgjDGGFOUJQhjjDFFWYIwxhhTlCUIY4wxRVmCMHVHRHJuRdq9IvKSiPxHEfG553pE5M/P8douEfm1c5xfKSKPu48/KSJfnGdsnxSRlQXP/1pEtsznPYxZLJ5tOWpMBZt2q9LOLOz6KhAH/sidg36ueehdwK+5r3kbEQmo6nHeWih3IT6JU9PoOICq/vYC3suYBbEWhKlrqnoap8zyXe5q1g+IyLcBROT9BftfvCgiMeBPcQrS7XH3g/ikiOwUkaeA77stjFcLfsQaEfmhuw/AH7nv+7ZrRORzIvJ5EbkZ6AH+3n3/qPvaHve620TkFXe/hfsKXj8hIn/itoaeEZF6LIZnPGAJwtQ9Ve3D2c+hc9apzwGfdlsb1wHTOEUbf+LujXG/e9124GZVfX+Rt78a+BXgCuCWmX/s54jjcZzWyyfc95+eOed2O92HU058G3CViHzUPd0IPKOqW4Ef4+zJYMyCWYIwZm5PA18Qkd8HWgrKeM/2vXOUjvieqg65/9j/E/DeC4zlKuCHbnHALPD3OHuWAKSBb7uPn8fpBjNmwSxBmLonIutxylK/rcqoqv4pTn2lKPC0iFwyx1tMnuPtZ9eyUZzaTYV/e5F5BXy2jL5VMyeHjS2aRWIJwtQ1EekA/hL4os4qTCYiG1T1FVW9D9gFXAKMA7F5/IgPu/sRR3F2EXsap4Bbp7uxThj4xYLr53r/54D3i0i7iPhxqur+aB5xGDNv9knD1KOoiOwBgjif5h8GvlDkus+IyAeBPLAX+Gf3cU5EXsLZe3jkPD/rOeAfcer8f2WmUqeI3OueOwa8XnD93wF/KSLTwLtnDqrqCRG5G6ecuADfUdV6LJttlpBVczXGGFOUdTEZY4wpyhKEMcaYoixBGGOMKcoShDHGmKIsQRhjjCnKEoQxxpiiLEEYY4wp6v8DeKGR1wcrIdsAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# 시험점수가 N(80, 5.2)(평균:80, 표준편차:5.2)인 정규분포에서 82점일 확률\n",
    "mu = 80\n",
    "std = 5.2\n",
    "# scipy 의 statistics 패키지를 이용하여 정규분포에서 원하는 값 계산\n",
    "# https://docs.scipy.org/doc/scipy/tutorial/stats.html\n",
    "rv = sp.stats.norm(loc=mu, scale=std)\n",
    "\n",
    "# 확률밀도함수(Probability density function)\n",
    "print(f\"f(82)={rv.pdf(82.0):.3f}\") \n",
    "# 누적분포함수(Cumulative distribution function): P(X <= 82): 82점 이하일 확률\n",
    "print(f\"F(82)={rv.cdf(82.0):.3f}\")\n",
    "# Survival Function (1-CDF): P(X >= 82): 82점 이상일 확률\n",
    "print(f\"1 - F(82)={rv.sf(82.0):.3f}\")\n",
    "# 기대값(Expted value), 분산 (Variance)\n",
    "print(f\"E(X)={rv.mean():.3f}, V(X)={rv.var():.3f}\")\n",
    "\n",
    "# 상위 % 를 가지는 값 구하기 \n",
    "# Percent Point Function (Inverse of CDF): P(X <= x) = 90% 일때, x의 값\n",
    "print(f\"Top 10% point with ppf: {rv.ppf(0.90):.3f}\")\n",
    "# Inverse Survival Function (Inverse of SF): P(X >= x) = 10% 일때, x의 값\n",
    "print(f\"Top 10% point with isf: {rv.isf(0.10):.3f}\")\n",
    "# 중위 90% 확률을 가지는 구간\n",
    "print(f\"중위 90% interval: {rv.interval(0.9)[0]:.3f} < x < {rv.interval(0.9)[1]:.3f}\")\n",
    "# 상위 5%, 하위 5% 점수 구간\n",
    "print(f\"상하위 5% interval with ppf: x < {rv.ppf(0.05):.3f}, {rv.ppf(0.95):.3f} < x\")\n",
    "print(f\"상하위 5% interval with isf: x < {rv.isf(0.95):.3f}, {rv.isf(0.05):.3f} < x\")\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 15,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 15,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEGCAYAAAB/+QKOAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAvpUlEQVR4nO3deZTcd3nn+/en9t5bS0u29tZu2fJGI5OAWQ2YkFgkAxNDmDEzTDyci0/IJTkTE3Ig1zmZA8kZyMyN54In8ZkJgTgsWZRg4hiw2YJtybZsIdmyWrtkLa2lN3Xt9dw/6tdKqd2SqqX6dXVXPa9z6qh+W/Ujqaue+n2X5yszwznnnJsoUu8AnHPOzUyeIJxzzk3KE4RzzrlJeYJwzjk3KU8QzjnnJhWrdwC1Mn/+fFuxYkW9w3DOuVnl2WefPWVmPZMda5gEsWLFCrZt21bvMJxzblaRdPBix7yJyTnn3KQ8QTjnnJuUJwjnnHOT8gThnHNuUqEmCEl3StotqV/S/Zc4799IMkl9Ffs+FVy3W9K7w4zTOefca4U2iklSFHgQeCdwBNgqaYuZ7ZpwXgfwCeDpin0bgLuB64FFwHclrTWzYljxOuecu1CYdxCbgH4z22dmOeARYPMk5/0B8HkgU7FvM/CImWXNbD/QH7yec865aRJmglgMHK7YPhLsO0/SrcBSM/v2VK8Nrr9X0jZJ2wYGBmoTtXMhMjOKJS+x72aHuk2UkxQBvgB85Epfw8weAh4C6Ovr83edm5GKZmw/leHF0xlOpMutpD2pKNfPTfK6nhbiEdU5QucmF2aCOAosrdheEuwb1wHcADwpCeAaYIuku6q41rlZ4VSmwD8cGOFEusjClig/v7AFCQ6O5Hny1TG2n8rw3uUdLG2P1ztU514jzASxFVgjqZfyh/vdwIfGD5rZEDB/fFvSk8Bvm9k2SWnga5K+QLmTeg3wTIixOldzR0bzfGPfMFHBL/d2sK47ef7Y7dfCgZEc/3RolL/qH+LOpe3cOC9Vx2ide63Q+iDMrADcBzwGvAR83cx2SnoguEu41LU7ga8Du4B/Aj7uI5jcbHJ4NM8j/UO0xsQ967ovSA7jVnQk+Mi6bpa1x3n00CjbTqbrEKlzF6dGWZO6r6/PvFifmwlOpQt8Zc8QbbEIv7ami7b4pb+HFc34+/0jvDKU447FbfQtaJmmSJ0DSc+aWd9kx3wmtXM1lCmU+Oa+YWKCf7uq87LJASAqsbm3g7VdCb579Bxb/U7CzRCeIJyrETPj24dGGc6V+JWVnXQno1VfW5kkvnf0HDtOZy5/kXMh8wThXI08czLNnqEcb1vcxuK2qY9KikpsXtHB8vY43zk0yv7hXAhROlc9TxDO1cDh0fKw1XXdCfp6rnw0UjQifnllB/NSUf52/wgnxgo1jNK5qfEE4dxVyhRL/MOBEbqTEd6zrJ1gXs8VS0UjfGBVJ8mo+MbeYUbzpRpF6tzUeIJw7io9cfQcI/kSv7S8g1S0Nm+pzkSUD6zqJFMsseXACKUGGW3oZhdPEM5dhX3DOV44nWXTghYWXUG/w6UsaInxrqXtHBrN89MTPrLJTT9PEM5doUyxxHcOjTIvFeX2a1tD+Rkb5ya5rjvBT46PcSrj/RFuenmCcO4KPXH0HKP5Eu9d1k4spIJ7krhjSTuJiPinQ6M0ysRWNzt4gnDuChwZzYfWtDRRWzzC2xa3ceRcgZfO+tBXN308QTg3RSUzHjs8Smc8whuvCadpaaIb5ybpSUX54bFzvp6EmzaeIJybomcHMgxkirxjSRuJ6PSs5SCJty5qYzBX4gWfZe2miScI56ZgNF/iR8fG6O2Is7YrMa0/e2VnnCVtMZ46kabofRFuGniCcG4Kvn/0HEUz3rnk6ifETZUk3rCwleF8iZfOZqf1Z7vm5AnCuSodHMmx62yW2xa2MDdVfSG+WlrVGWd+KsrTJ9I+osmFzhOEc1UomvH4kXN0JSL83MLp6ZiejCQ2LWhhIFPk4Gi+bnG45uAJwrkqPDuQ4VSmyB1L2oiHNOehWhvmJElFxfZT3lntwhVqgpB0p6Tdkvol3T/J8Y9J2iFpu6QfS9oQ7F8hKR3s3y7pS2HG6dyljBVK/OT4GCs74qzpeu3SodMtFhEb5yZ5ZTDnhfxcqEJLEJKiwIPAe4ANwAfHE0CFr5nZRjO7Gfgj4AsVx/aa2c3B42Nhxenc5fz42Bi5ovH2xW31DuW8m+enKIEvLORCFeYdxCag38z2mVkOeATYXHmCmQ1XbLYB3uvmZpRTmQLPn8pw8/wU81ti9Q7nvHmpGMva47xwOuOd1S40YSaIxcDhiu0jwb4LSPq4pL2U7yB+o+JQr6TnJf1A0u2T/QBJ90raJmnbwMBALWN3DijXW0pExO3TNGN6Km6Ym2QwV+KYLyrkQlL3Tmoze9DMVgG/A/xesPsYsMzMbgE+CXxNUuck1z5kZn1m1tfT0zN9QbumcGA4x97hPD9/TQut8bq/VV5jXXeCmOBnZ3xOhAtHmL/1R4GlFdtLgn0X8wjwPgAzy5rZ6eD5s8BeYG04YTr3WmbGk8fG6ExEeF1PS73DmVQyGmF1V4KXBrM+s9qFIswEsRVYI6lXUgK4G9hSeYKkNRWb7wX2BPt7gk5uJK0E1gD7QozVuQvsGcpxfKzAm65pDa2Udy1cPzdJumDsH/Y5Ea72Qut1M7OCpPuAx4Ao8LCZ7ZT0ALDNzLYA90m6A8gDZ4F7gsvfDDwgKQ+UgI+Z2ZmwYnWukpnxo2NjzElGuGFu/Ye1XsrKjgSpqNh1Nsvqaa4N5RpfqMMyzOxR4NEJ+z5T8fwTF7nuW8C3wozNuYt5eTDHQKbIXcs7iExzvaWpikbEdXOS7DidIVtsI1mjNbGdgxnQSe3cTFIK7h56UlGumzM7vpFfPydJweCVQV9MyNWWJwjnKuw8k+VMtsibrm2d9mqtV2pxW4yuRISdXuHV1ZgnCOcCZsbTJ9P0pKLTvtbD1ZDKzUwHR/KMFbz0hqsdTxDOBfYN5zmVKXLbwpZZc/cwbn13EgP2eDOTqyFPEM4FnjmZpiMe4bo5M3vk0mQWtkTpTkR4edCbmVzteIJwDjg+VuDgaJ6+nhTRWXb3AOVmpnXd5WamtDczuRrxBOEcsPVkmkRE3DQvVe9Qrtj6OQlKlCf5OVcLniBc0xvOFXnpbJab5iVJxWbvW+KalvJoJm9mcrUye98NztXIswMZDOhbMDNrLlVrvJnpwEiejDczuRrwBOGaWrFk7DiTYU1Xgq5EtN7hXLX13QlK5s1MrjY8Qbimtmcox1jBZnXfQ6VrW2N0xr2ZydWGJwjX1F44naEjHqG3M17vUGqi3MyUKDczFb2ZyV0dTxCuaQ3liuwfyXPjvOSML8o3FevnJCka9Hszk7tKniBc03rxdAaAGxukeWncotYYHfEIL/usaneVPEG4plQyY8fpLL0d8YbonK403sy0fzhH1puZ3FXwBOGa0v7hPMP5UsN0Tk+0rtubmdzV8wThmtKLZzK0xMSaWVS1dSqWtMVoj0XY7c1M7iqEmiAk3Slpt6R+SfdPcvxjknZI2i7px5I2VBz7VHDdbknvDjNO11yyxRJ7h3Jc150kOoPXm74akljbnWDfcI5c0eodjpulQksQkqLAg8B7gA3ABysTQOBrZrbRzG4G/gj4QnDtBuBu4HrgTuB/Bq/n3FXrH8pRMGZl1dapWB+sNLd32O8i3JUJ8w5iE9BvZvvMLAc8AmyuPMHMhis224DxrzqbgUfMLGtm+4H+4PWcu2ovDeboiEdY0hbqkux1t6QtRltMPmnOXbEwE8Ri4HDF9pFg3wUkfVzSXsp3EL8xxWvvlbRN0raBgYGaBe4aV6ZQYv9wjnXdiVm3KNBURYLaTHuHvJnJXZm6d1Kb2YNmtgr4HeD3pnjtQ2bWZ2Z9PT094QToGsqeoRzFJmheGreuO0HBYJ83M7krEGaCOAosrdheEuy7mEeA913htc5V5aXBLJ2JCItaG7t5adzS9jit3szkrlCYCWIrsEZSr6QE5U7nLZUnSFpTsfleYE/wfAtwt6SkpF5gDfBMiLG6JpAulDgwnOe67mTDNy+Ni0is7UqydzhHvuTNTG5qQvsaZWYFSfcBjwFR4GEz2ynpAWCbmW0B7pN0B5AHzgL3BNfulPR1YBdQAD5uZsWwYnXNYfdgjhLN07w0bv2cBNtPZ9g7nGN9d3P93d3VCfU+28weBR6dsO8zFc8/cYlr/xD4w/Cic83m5cEs3YkIC1uaa8T0svY4LTHxyqAnCDc1de+kdm46ZIslDo3mWdtEzUvjys1MifL8D29mclPgCcI1hQMjeUoGqxpk3YepWtedJFcy9o/4aCZXPU8QrinsHc6RjIgl7c2ZIJa3x0lG5bWZ3JR4gnANz8zYN5RnRWecaJM1L42LRsqFCfcM5Sh6M5OrkicI1/BOpIuMFkqs6mzMyq3VWtedIFs0Do7m6x2KmyU8QbiGN16srtkTRG9HgkRE7PZJc65KniBcw9s7lOPa1hht8eb+dY9FxKrOOHuGcpTMm5nc5TX3O8Y1vLF8iVfHCk1/9zBuXXeSsYJx2JuZXBU8QbiGdr55qas5Ry9NtLIzQUz4aCZXFU8QrqHtG87RFhPXtDRHcb7LSUTFys4ErwzmMG9mcpfhCcI1LDPjwGie3s7GX/thKtZ3JxktlDh6rlDvUNwM5wnCNaxTmSLpgrGsSSfHXcyqrjhR4aOZ3GV5gnAN61DQEesJ4kLJaIQVHXF2ezOTuwxPEK5hHR7N0xmP0JXwX/OJ1ncnGc6XOD7mzUzu4vyd4xqSmXFoNM/S9rj3P0xiTVeCCD6ayV2aJwjXkE5ni4wVjGUd3rw0mVQswvKOOC8PZr2ZyV2UJwjXkA6NeP/D5azrTjKYK3Ey7Ys1usmFmiAk3Slpt6R+SfdPcvyTknZJelHS9yQtrzhWlLQ9eGyZeK1zl3J4NE9HPEK39z9c1NquBAJ2D/loJje50N49kqLAg8B7gA3AByVtmHDa80Cfmd0IfBP4o4pjaTO7OXjcFVacrvGM9z8s8/6HS2qNR1jSHmOP90O4i6gqQUjaeAWvvQnoN7N9ZpYDHgE2V55gZk+Y2Viw+RSw5Ap+jnMXOJMtcq5gLPXmpcta3ZlgIFNkKOfNTO61qr2D+J+SnpH0f0nqqvKaxcDhiu0jwb6L+SjwnYrtlKRtkp6S9L7JLpB0b3DOtoGBgSrDco3O5z9Ub01XEoD+Ib+LcK9VVYIws9uBXwOWAs9K+pqkd9YqCEkfBvqAP67YvdzM+oAPAX8iadUkcT1kZn1m1tfT01OrcNwsd3i0QHsswpyk9z9cztxUlLnJqCcIN6mq30Fmtgf4PeB3gLcA/0PSy5J+5SKXHKWcUMYtCfZdQNIdwKeBu8zsfG+ZmR0N/twHPAncUm2srnmZGYdG8izr8P6Haq3uSnBoNE+2WKp3KG6GqbYP4kZJXwReAt4O/JKZXRc8/+JFLtsKrJHUKykB3A1cMBpJ0i3Alyknh5MV++dISgbP5wNvBHZN6W/mmtLZbInRQoml7V69tVqrOxMUDQ6M+BoR7kLVvov+X+DPgN81s/T4TjN7VdLvTXaBmRUk3Qc8BkSBh81sp6QHgG1mtoVyk1I78I3g296hYMTSdcCXJZUoJ7HPmZknCHdZ3v8wdUvaY6SiYs9QjnXdyXqH42aQahPEeykPOy0CSIoAKTMbM7OvXOwiM3sUeHTCvs9UPL/jItf9C3AlI6dckzs8mqctJuYmo/UOZdaISKzqTLB3uLwUacSb5lyg2j6I7wItFdutwT7nZgyf/3DlVnclSBeMV32NCFeh2gSRMrPR8Y3geWs4ITl3ZQZzJUbyJZ//cAV6O+NEgP5hH83k/lW1CeKcpFvHNyS9Dkhf4nznpt35/gcv0DdlqWiEJe1x9nmCcBWq7YP4Tcodya8CAq4BfjWsoJy7EodG8rTGxDzvf7giKzvjPPnqGCP5Ih1x/zd0VSYIM9sqaT2wLti128x8TJybMcyMw97/cFVWdiZ48tUx9g/nuXGeJwg3tWJ9rwduBG6lXHjv34cTknNTN5QrMez9D1elJxWlPRZhvzczuUBVdxCSvgKsArYD41W9DPiLcMJybmp8/sPVk0RvZ5w9Qz7c1ZVV2wfRB2wwX3rKzVCHRvO0xMT8lDeNXI2VnQl2nMlybKzA4jZPts2u2iamn1HumHZuRvL5D7WxoiOOwEczOaD6O4j5wC5JzwCVBfV8IR9Xd4PZIsO5EpsW+Dfeq9USi3Bta4z9w3luv7be0bh6qzZB/H6YQTh3NQ57/0NNrexM8OPjY6QLJVpiXjK9mVW7HsQPgANAPHi+FXguxLicq9qh0TypqOjx/oeaWNlZTrT7vbpr06u23PevU14z+svBrsXA34UUk3NT4v0PtXVNa7m6q/dDuGrvHz9OeU2GYTi/eNCCsIJyrlpDuSJDOZ//UEsRid6OOAeG8/jAxeZWbYLImtn5rxOSYpTnQThXV97/EI4VnQlGCyUGMsXLn+waVrUJ4geSfhdoCdai/gbwD+GF5Vx1Do6U+x8WtHj/Qy31BgUPfVZ1c6s2QdwPDAA7gP9MeRGgSVeSc266mBkHR/Is9/Wna64zEWV+KurLkDa5akcxlczsf5nZB8zs/cHzyzYxSbpT0m5J/ZLun+T4JyXtkvSipO9JWl5x7B5Je4LHPVP7a7lmcDZbrr+0wst7h2JFR5zDo3nyJW9NblbVjmLaL2nfxMdlrokCDwLvATZQLvC3YcJpzwN9ZnYj5VFSfxRcOxf4LHAbsAn4rKQ5U/mLucZ3YKTc/LG8PVHnSBpTb0eCgsGRUb+LaFZTqcU0LgV8AJh7mWs2Af1mtg9A0iPAZmDX+Alm9kTF+U8BHw6evxt43MzOBNc+DtwJ/FWV8bomcHA0T2c8wpykT+YKw7KOOFGV50P0dnoSbkbVNjGdrngcNbM/Ad57mcsWA4crto8E+y7mo8B3pnKtpHslbZO0bWBg4HJ/DddAvP8hfPGIWNIW947qJlZtue9bKzYjlO8oqr37qOb1Pxy85lumcp2ZPQQ8BNDX1+cNpU3kRLpIpmje/xCyXl9lrqlV+yH/3yqeFyiX3fi3l7nmKLC0YntJsO8Cku4APg28xcyyFde+dcK1T1YZq2sC5/sfOrzpI0y9HQmeZIwDw3k2+ipzTafaJUffdgWvvRVYI6mX8gf+3cCHKk+QdAvl8h13mtnJikOPAf+1omP6XcCnriAG16AOjuSZn4rSHvf+hzAtaInSGhP7R/JsnJeqdzhumlXbxPTJSx03sy9Msq8g6T7KH/ZR4GEz2ynpAWCbmW0B/hhoB74RtCMfMrO7zOyMpD+gnGQAHhjvsHauUCqvP33TfP/ACpskejsS7B/JYWbe39NkpjKK6fXAlmD7l4BngD2XusjMHqU8qa5y32cqnt9xiWsfBh6uMj7XRF49V6BgeP/DNOntjLPzbJYT6SLXtNas69HNAtX+by8BbjWzEQBJvw9828w+fMmrnAvBgZEcAi/QN01WBP08+4dzniCaTLUNuAuByrFuuWCfc9Nu73COxW0xUlHvf5gO7fEIPamorw/RhKr9OvAXwDOS/jbYfh/wf0KJyLlLGMkXOZEu8tZFrfUOpams7EywdSBNrmgkot4P0SyqnSj3h8B/AM4Gj/9gZv81zMCcm8y+ofK32JU+s3da9XbEKdm/lld3zWEq9+itwLCZ/XfgSDB81blp1T+cozNo8nDTZ0l7nJhg34jPqm4m1Rbr+yzwO/zrXIQ48JdhBeXcZAqlcnmNlZ0JH245zWIRsbS9vMqcax7V3kH8MnAXcA7AzF4FOsIKyrnJHBzJkysZa7q8eakeejsTnM4WGcr5KnPNotoEkQvWfzAASW3hheTc5F4ZypKIiOU+/6EuxleZ80WEmke1CeLrkr4MdEv6deC7wP8KLyznLlQyY89QjpWdcWIRb16qh/HSJl7dtXlcdpiryo29fw2sB4aBdcBnzOzxkGNz7rxXzxUYKxhru5P1DqVplctuxHllKEfRjKj3AzW8yyYIMzNJj5rZRsCTgquL3YNZIoKVnd68VE+ruxLsOJPlyGjeK+k2gWqbmJ6T9PpQI3HuIsyMlwdzrOxI+OzpOuvtSBAV9A95M1MzqPbddhvwlKS9kl6UtEPSi2EG5ty4I+cKjORLXDfHv7HWWyIqlrXH6fd+iKZwySYmScvM7BDlNaKdq4uXzmaJCdZ0ef/DTLC6K8HjR85xOlNgXsqL9zWyy91B/B2AmR0EvmBmBysfoUfnml7JjJcHs6zuSngNoBlidTAPxZuZGt/lEkTlO3JlmIE4N5mDI3nGCsaGOX73MFN0JaL0pKLezNQELpcg7CLPnZsWu85mSUbkxflmmNVdCY6MFsgUSvUOxYXocgniJknDkkaAG4Pnw5JGJA1f7sUl3Slpt6R+SfdPcvzNkp6TVJD0/gnHipK2B48tE691ja9QMl4ZzLG2O+GT42aY1V0JjPLaHK5xXbKHycyuuGSmpCjwIPBO4AiwVdIWM9tVcdoh4CPAb0/yEmkzu/lKf76b/fYN58iWjOu8eWnGWdQaozUm+odyXD/X1wZvVGEOKt8E9JvZPjPLAY8AmytPMLMDZvYi4Pep7jV2nc3SEpOvPT0DSWJ1Z4J9w3kKJW99blRhJojFwOGK7SPBvmqlJG2T9JSk99U0MjfjpQsl9gzluH5OkoiXdJiR1nUnyZbMi/c1sJk8LXW5mfUBHwL+RNKqiSdIujdIItsGBgamP0IXml1nsxQNNnrzxYy1oiNOKipeOputdyguJGEmiKPA0ortJcG+qpjZ0eDPfcCTwC2TnPOQmfWZWV9PT8/VRetmlB1nsixoibKw1SdizVTRiFjblaB/KOfNTA0qzASxFVgjqVdSArgbqGo0kqQ5kpLB8/nAG4Fdl77KNYqBdIHjYwW/e5gF1s8pNzPt96VIG1JoCcLMCsB9wGPAS8DXzWynpAck3QUg6fWSjgAfAL4saWdw+XXANkkvAE8An5sw+sk1sB1nypVbr5/ro5dmuuUdcVqi4uWzniAaUaj372b2KPDohH2fqXi+lXLT08Tr/gXYGGZsbmYqmrHzTIbVnQlaYzO5i8wBRCXWdid46WyOfMmI+3yVhuLvQDej7BvOca5gbJzndw+zxXXdSXIl85XmGpAnCDej7DidpTXmpTVmk2UdcVpi4uVBTxCNxhOEmzHGCiX6h8tzH3w5y9kjIrGuK8meoSy5oo9maiSeINyMsetMlpLBxnk+emm2uWFuknwJXh70ORGNxBOEmzF2nMlwTUuMBS0+92G2WdwWY24yyo4zmXqH4mrIE4SbEU6MFTiRLnKDd07PSpLYODfJ4dECZ7PFeofjasQThJsRXjidISq43iu3zlo3zE0iYMdpv4toFJ4gXN3lS8bOs1nWdydp8bkPs1ZHIkpvR5wdZ7KUzDurG4G/G13dvXw2S7Zo3DTfO6dnu43zUozkSxz0Cq8NwROEq7vtpzPMTUZZ2uad07Pdmq4Eqah40ZuZGoInCFdXA+kCR88VuGleEvnch1kvFhEb5iR5ZShH2ternvU8Qbi6euF0hoh83YdGcvP8FEUr/9+62c0ThKubQsn42Zks67oStMb9V7FRLGiJsaw9znOnMt5ZPcv5u9LVze7BLBnvnG5It/akGM6V6B/y+kyzmScIVzfbT2foTkRY3h6vdyiuxtZ2JeiIR3h2wJuZZjNPEK4uTmcKHB4tcNO8lHdON6CIxC3zUxwczXMqU6h3OO4KeYJwdfHC6SwRvDBfI7t5Xoqo4Dm/i5i1Qk0Qku6UtFtSv6T7Jzn+ZknPSSpIev+EY/dI2hM87gkzTje98iXjxdMZ1nQnaPfO6YbVGo9w3ZwkO85kyPiQ11kptHenpCjwIPAeYAPwQUkbJpx2CPgI8LUJ184FPgvcBmwCPitpTlixuum162y5c/pW75xueK/vaSFfgudO+V3EbBTm17dNQL+Z7TOzHPAIsLnyBDM7YGYvAhO/XrwbeNzMzpjZWeBx4M4QY3XTxMx4diBNTyrKMu+cbngLW2Os7IizbSBNvuRDXmebMBPEYuBwxfaRYF/Y17oZ7Mi5AifTRV7X0+Kd003iDQtbGSuYV3mdhWZ1A7CkeyVtk7RtYGCg3uG4Kjw7kCYVFdfP9bLezWJpe4zFbTGePpn2iXOzTJgJ4iiwtGJ7SbCvZtea2UNm1mdmfT09PVccqJsew7kiuwdz3DgvRTzidw/NQhJvWNjCUK7ES2d9SdLZJMwEsRVYI6lXUgK4G9hS5bWPAe+SNCfonH5XsM/NYtuDjkrvnG4+qzsTzE9FeepEGvO7iFkjtARhZgXgPsof7C8BXzeznZIekHQXgKTXSzoCfAD4sqSdwbVngD+gnGS2Ag8E+9wslS8Zz5/OsLorQXcyWu9w3DQbv4sYyBR5xctvzBqhFuA3s0eBRyfs+0zF862Um48mu/Zh4OEw43PTZ8fpDOmCsWlBS71DcXWyYU6Snx5P86NjY6zpShDxQQoz3qzupHazQ8mMZ06mWdQaY4kvCtS0IhK3X9vKqUzR+yJmCU8QLnSvDOYYzJW4baEPbW1267oTLGiJ8qNjYxS9L2LG8wThQmVmPH0yzZxkhDVdiXqH4+pMEm++to3BXIkdp/0uYqbzBOFCdWg0z7GxApsWtHibswNgVWecRa0xfnJ8jILPrp7RPEG4UD1zMk1rTNzgS4q6gCTevKiVkXyJZwfS9Q7HXYInCBea42MF9g7neV1Pi0+McxdY0ZFgVWecfzmeZizvlV5nKk8QLjQ/PTFGMiJe5xPj3CTetriNXMn48fGxeofiLsIThAvFQLrA7sEcr+tJkYr5r5l7rfmpGLfMT/H8qQyn0r7q3Ezk71wXip+eSBOPQJ9PjHOX8KZrW0lExfdfPVfvUNwkPEG4mjsTTIS6dX4LrX734C6hNRbh5xe2sG84z14vwTHj+LvX1dxPT4wRFbze7x5cFfp6WpibjPL4kVFfVGiG8QThaupstsjOM1lump/y9aZdVaIR8a6l5clzT53wDuuZxN/BrqZ+fGyMiODnFrbWOxQ3i6zoSLBhTpKnTqQ5kynWOxwX8AThauZkusDOs1n6elr87sFN2dsXtxGVePzIqK8ZMUP4u9jVzI+Olec93LbQ+x7c1LXHI9x+bSv7R/LsHvQO65nAE4SriVfP5dkzlGPTwhZafOSSu0Kv60mxoCXK946eI1v0Gdb15u9kVxM/PDZGa0z09fisaXflIhLvXtrOSL7ET457naZ68wThrlr/UI4DI3l+bmEryaj/Srmrs7gtzk3zkmw9mebYWL7e4TS1UN/Nku6UtFtSv6T7JzmelPTXwfGnJa0I9q+QlJa0PXh8Kcw43ZUrlIzvHhllXirKrX734GrkbYvaaItHePTgKEWfG1E3oSUISVHgQeA9wAbgg5I2TDjto8BZM1sNfBH4fMWxvWZ2c/D4WFhxuqvz9Mk0g7kS7wxGoDhXC6lYhHcvbWMgU+SnJ7ypqV7CvIPYBPSb2T4zywGPAJsnnLMZ+D/B828C75CvSTlrDOWK/PT4GOu6E6zo9NXiXG2t6UqyYU6Sfzk+xkkv5lcXYSaIxcDhiu0jwb5JzzGzAjAEzAuO9Up6XtIPJN0+2Q+QdK+kbZK2DQwM1DZ6d1nfP1ousPb2xW11jsQ1qjuWtJGKiW8fHPGmpjqYqT2Kx4BlZnYL8Enga5I6J55kZg+ZWZ+Z9fX09Ex7kM1s92CW3YM5fv6aVroS0XqH4xpUayzCu5e2cyJd5Ee+bsS0CzNBHAWWVmwvCfZNeo6kGNAFnDazrJmdBjCzZ4G9wNoQY3VTcC5f4rHDoyxsiXKbF+RzIVvXneSmeeUyHAdHfALddAozQWwF1kjqlZQA7ga2TDhnC3BP8Pz9wPfNzCT1BJ3cSFoJrAH2hRirq5KZ8eihEbJF4xeXdxD1pUTdNHjH4nbmJqP848FR0gWfQDddQksQQZ/CfcBjwEvA181sp6QHJN0VnPbnwDxJ/ZSbksaHwr4ZeFHSdsqd1x8zszNhxeqq99SJNHuH87x9cRs9LbF6h+OaRCIq7lrRwblCiX867LWaposa5R+6r6/Ptm3bVu8wGtq+4Rzf2DvM+u4Ed63owAecuen29Ikxnnh1jLctauU2rxhcE5KeNbO+yY7N1E5qN8OcGCvwd/tHWNAS5T3LPDm4+ti0oIX13QmefHWM/cPeHxE2TxDusk5lCvz13iGSUfH+VZ0kop4cXH1I4heWdTA/FeXvD4wwmPW1I8LkCcJd0kC6wF/tGULA3as76Yj7kFZXX4mo+JWV5VHv39o37FVfQ+QJwl3UwZEcf7lnCEl8cHUX81LeKe1mhjnJKJtXdHA6U+Rb+0Yo+CS6UHiCcK9hZjxzMs0j/cO0xyP8u7VdzPcRS26G6e1M8AvL2zk0mufv9nuSCIO/690FhnNFvnNolP0jedZ2JXjv8nYv4e1mrBvmpsgVjX8+co6/2T/M+1Z4H1kteYJwAGSKJZ4+kWbryTQSvHNJG7fOT/loJTfj3drTQkTiscOjfHXPIO9f2UmHl3+pCU8QTS5TKPHC6QxPnUiTLhob5iR587WtdCf9DeZmj5vnp2iPR/j7A8M8vHuQX1jWzpquZL3DmvU8QTSp42MFnjuVZteZLAWDFR1x3rqojWta/VfCzU6ruxLcs66bLQdG+Na+EdZ3Z3nb4jYvJnkV/NOgiRTNeGUwx7aBNEfPFYhH4Pq5SW6d38JCTwyuAcxPxfj3a7t56kSap06M8cpQjhvmJHnDwlbmpjxRTJV/KjSBTKHE86cyPHcqw0i+xJxkhHcsbmPj3CSpmHdAu8YSi4g3XdvKxnlJnj6R5sXTGV48k2VNV4Jb5qfo7Yh731qVPEE0sEyhxNaBNNtOZsiWjBUdcd69tJ1Vnf4GcY2vKxHlXUvbeeM1rWwbSLP9dIY9Qzm6ExFumpfixnkp2uL+BelSPEE0oImJYV13gp9f2OrNSK4ptcUjvGVRG2+8ppVXhnI8fyrND46N8aPjY6ztSnDz/BTL2/1L02T8E6OBnE8MAxmyRWNtV4I3XdvKAp/k5hyxiNgwp7zO9elMge2nMuw4k+XlwRxzkhFunpdi47wUrd7sep5/cjSA0XyJ5095YnCuWvNSMd6xpJ03L2pj92CW7acyPPHqGD84NsbKzgQ3zEmyqitBvMkXxPJPkFmqUDIOjuR5IWhXNWBtV4I3XuNNSc5VKx4RN8xNccPcFAPpAjvOZNl1Nkv/UI5kRKztTrC+O8nyjjixJkwW/kkyS+SKxkCmwPGxAvuGcxwazZMvQWtMbFrQwk3zUj6Mz7mr0NMS4+2LY7x1USuHRvPsPJNl92COHWeyxCPQ25FgZWeCZe1x5iQjTdFnEWqCkHQn8N+BKPBnZva5CceTwF8ArwNOA79qZgeCY58CPgoUgd8ws8fCjHU6mBm5kpEpGpmCkS0a2VKJQgnyJSNfMgolI1+CXMkYzZcYzZcYyhUZyv1rSePuRISNc1Os7EzQ2xH3daGdq6GIxIqOBCs6Erx7aflOvX84R/9QjleGyosUtccjLGqN0dMSZUFLjHnJKB2JSMPVLQstQUiKAg8C7wSOAFslbTGzXRWnfRQ4a2arJd0NfB74VUkbgLuB64FFwHclrTWzaVsdxMwwKD+s/GehVP6AzxfLH+a58Ucx+NAvlj/0M8VS+c9CxfPgWLX1JmMq/xKO/yLeOC/GguCX0WeGOjc9YhGxqivBqq4E71pinM2WODSa59BonuNjhfMJY1wyKtpiEZJRkYyKVFQkoiImEYuImCAa/BmLiKhELAIxiej5P4PzgmPRSa6drruXMO8gNgH9ZrYPQNIjwGagMkFsBn4/eP5N4E9V/ptvBh4xsyywX1J/8Ho/rXWQY/kS/9+uM+eTgBlczfIj8QgkoxFSwS9IezzC/FTk/C9LMipSsQu348EvQDx4xCLlbzHOuZlDEnNTUeamotw8PwWU7/wH0gUGcyWGc0WGcyXGCuUvhdmiMZIrPy9YuXWgUKOK5FFBZcPBta1xPrSmqzYvXiHMBLEYOFyxfQS47WLnmFlB0hAwL9j/1IRrF0/8AZLuBe4NNkcl7a5N6MwHTtXotWrJ45oaj6t6MzEm8Liq9mvlP64kruUXOzCrO6nN7CHgoVq/rqRtZtZX69e9Wh7X1Hhc1ZuJMYHHNVW1jivMHpWjwNKK7SXBvknPkRQDuih3VldzrXPOuRCFmSC2Amsk9UpKUO503jLhnC3APcHz9wPfNzML9t8tKSmpF1gDPBNirM455yYIrYkp6FO4D3iM8jDXh81sp6QHgG1mtgX4c+ArQSf0GcpJhOC8r1Pu0C4AH5/OEUyE0GxVIx7X1Hhc1ZuJMYHHNVU1jUvlL+zOOefchRprVodzzrma8QThnHNuUp4gLkPSb0kySfPrHQuApD+Q9KKk7ZL+WdKiescEIOmPJb0cxPa3krrrHROApA9I2impJKmuwxIl3Slpt6R+SffXM5Zxkh6WdFLSz+odSyVJSyU9IWlX8P/3iXrHBCApJekZSS8Ecf0/9Y5pnKSopOcl/WOtXtMTxCVIWgq8CzhU71gq/LGZ3WhmNwP/CHymzvGMexy4wcxuBF4BPlXneMb9DPgV4If1DKKi9Mx7gA3AB4OSMvX2v4E76x3EJArAb5nZBuANwMdnyL9XFni7md0E3AzcKekN9Q3pvE8AL9XyBT1BXNoXgf8CVZdQCp2ZDVdstjFDYjOzfzazQrD5FOW5K3VnZi+ZWa1m2F+N86VnzCwHjJeeqSsz+yHlEYQzipkdM7PngucjlD/4XlNNYbpZ2WiwGQ8edX8PSloCvBf4s1q+rieIi5C0GThqZi/UO5aJJP2hpMOUZ9fPlDuISv8R+E69g5hhJis9U/cPvNlA0grgFuDpOocCnG/K2Q6cBB43s5kQ159Q/jJ7NaXkXmNWl9q4WpK+C1wzyaFPA79LuXlp2l0qLjP7ezP7NPDpoCT6fcBnZ0JcwTmfptw88NXpiKnauNzsJKkd+BbwmxPunusmmJN1c9DP9reSbjCzuvXhSPpF4KSZPSvprbV87aZOEGZ2x2T7JW0EeoEXgrK6S4DnJG0ys+P1imsSXwUeZZoSxOXikvQR4BeBd9g0TrCZwr9XPXn5mCmSFKecHL5qZn9T73gmMrNBSU9Q7sOpZyf/G4G7JP0CkAI6Jf2lmX34al/Ym5gmYWY7zGyBma0wsxWUmwNunY7kcDmS1lRsbgZerlcslYLFof4LcJeZjdU7nhmomtIzLhCU/f9z4CUz+0K94xknqWd8hJ6kFsrr3dT1PWhmnzKzJcFn1d2USxZddXIATxCz0eck/UzSi5SbwGbE8D/gT4EO4PFgCO6X6h0QgKRflnQE+Dng25LqsjJh0IE/XnrmJeDrZrazHrFUkvRXlNdZWSfpiKSP1jumwBuBfwe8Pfh92h58Q663a4EngvffVsp9EDUbVjrTeKkN55xzk/I7COecc5PyBOGcc25SniCcc85NyhOEc865SXmCcM45NylPEK4pSSoGQyd3BpU5f0tSJDjWJ+l/XOLaFZI+dInjiyR9M3j+EUl/OsXYPlJZpVfSn82QQnWuyTT1TGrX1NJBRVwkLQC+BnQCnzWzbcC2S1y7AvhQcM0FJMXM7FXKa6xfqY9Qnpn7KoCZ/aereC3nrpjfQbimZ2YngXuB+1T21vGa+pLeUjFR63lJHcDngNuDff938I1/i6TvA98L7jAqSy8slfSkpD2SPhu87gXnSPptSb8v6f1AH/DV4PVbgmv7gvM+KGlHMFny8xXXjwZFHF+Q9JSkhWH/u7nG5wnCOcDM9gFRYMGEQ78NfDy427gdSAP3Az8ys5vN7IvBebcC7zezt0zy8puAfwPcCHxAl1i4yMy+Sfnu5deC10+PHwuanT4PvJ3yWgSvl/S+4HAb8FSwTsEPgV+v8q/u3EV5gnDu0n4CfEHSbwDdFWteTPS4mV1sXYXHzex08GH/N8CbrjCW1wNPmtlAEMdXgTcHx3KUF5ACeJZyM5hzV8UThHOApJVAkXKN//PM7HPAfwJagJ9IWn+Rlzh3iZefWM/GKJdEr3z/paYU8GvlKyroFvH+RVcDniBc05PUA3wJ+NOJZcolrQqq+36ecnG29cAI5cKE1XqnpLlB9c/3Ub4rOQEskDRPUpJymfRxF3v9Z4C3SJqv8hKmHwR+MIU4nJsS/5bhmlVLsCpYnPK3+a8Ak5WV/k1Jb6O8UtdOyivllYCipBcor+l89jI/6xnK6xosAf4yGCWFpAeCY0e5sGT0/wa+JClNuQotUF6GU9L9wBOAgG/7gkguTF7N1Tnn3KS8ick559ykPEE455yblCcI55xzk/IE4ZxzblKeIJxzzk3KE4RzzrlJeYJwzjk3qf8fYRcQMUlsHeYAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# 표준정규분포 (Z-distribution) N(0,1)\n",
    "rv = sp.stats.norm(loc=0, scale=1)\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "**Q-Q Plot (Quantile-Quantile Plot)**\n",
    "\n",
    "정규분포인지를 살펴보기 위한 다른 시각화 방식은 Q-Q Plot 입니다. Q-Q Plot 은 정규분포와 실제 데이터의 같은 Quantile 상의 데이터를 샘플링해 point를 찍어 봄으로써 두 분포가 유사한지를 시각화하여 판단하는 방식입니다. point 들이 직선을 이룬다면 두 분포는 같은 정규분포일 가능성이 높습니다.\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 16,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAEGCAYAAABvtY4XAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAqKElEQVR4nO3dd3hVVdbH8e8KoIDyWoCxUmxDFVBiw44duzIq4gxiYQBBBBQLjh3BgqggMNhLFEVwVBS7KIotIII0FYcgjCigKIpSkvX+cW7gEnJzT0Juze/zPPe55bSVq1ns7LX3PubuiIhI9slJdQAiIpIYSvAiIllKCV5EJEspwYuIZCkleBGRLFU91QFEq1evnjdu3DjVYYiIZIxp06Ytd/f6pW1LqwTfuHFj8vPzUx2GiEjGMLOCWNsS2kVjZn3NbLaZfWlmz5hZzUReT0RENkpYgjez3YDLgVx3bwlUA85L1PVERGRTiS6yVgdqmVl1oDbwvwRfT0REIhKW4N19CXA3sAj4HvjF3d8ouZ+ZdTOzfDPLX7ZsWaLCERGpchLZRbMDcDqwB7ArsI2ZXVByP3cf4+657p5bv36phWAREamARHbRHAv8192Xufs6YALQLoHXExHJOnl50Lgx5OQEz3l54Y9N5DDJRcDBZlYb+AM4BtAYSBGRkPLyoFs3WL06eF9QELwH6Nw5/vGJ7IP/BHgemA7MilxrTKKuJyKSbQYODJK7UUQtgiy/enXweRgJHUXj7je6e1N3b+nuf3f3NYm8nohINlm0CFrxBR9wGPdz+Safh6G1aERE0tGqVYzZth/TaMs+fM37HLFhU8OG4U6hBC8ikk7cYdw4aNqUi3+7l8eqX0IT5vMk/wCgdm0YNCjcqZTgRUTSxTffwEknwTnnwF/+gk2dSq3HRvN/jXbEDBo1gjFjwhVYIc0WGxMRqZL+/BPuuAMGD4attoJ774XLLoPq1el8cPiEXpISvIhIKr35JvTsGbTezz0X7rkHdt21Uk6tLhoRkVT43/+ChH788cH711+HsWMrLbmDEryIVFFlzRCNN3s07OzSUvdbvx7uuw+aNoUXX4Sbb4ZZszYm+srk7mnzaNu2rYuIJNpTT7nXru0eDFkJHrVrB5+XtS3esfGuceTWH/mKRm2CNyec4P7111v8swD5HiOnWrA9PeTm5rru6CQiida4cTDtv6RGjYLnWNsWLiz72IULS7/GDvzEYK7lUh7kx2q7sPPY++Dss8Fsi34OADOb5u65pW1TF42IVDmxZoIuWlT2tnjHbv7e6cJjzKcJF/Mw93IFfy2cBx07Vkpyj0cJXkSqnFgzQRs2LHtbvGOjHbPzbN7jSB6jK1+zD22ZRn/uYcdGdSoWdAUowYtI1itZ7OzQIZgRGq14huigQbG3Qfzt/P47XH01r//YhhbM5hIe5DA+YCatyzULtVLE6pxPxUNFVhGpbLGKoj16uDdq5G4WPEcXSZ96Kva2mNuLitxfeMG9QYPgIhdd5ONGLSvzPJUBFVlFpKoKWxTdIv/9L/TuDa+8Ai1bwqhRcNhhlXTysqnIKiJVVtiiaIWsXQu33w4tWsDkyXDXXTB9etKSezxaqkBEslrDhqW34MMuuRvTu+8GSwzMmwdnnRWsH9OgwRaetHKpBS8iWS1uUbS8fvgBLrgA2reHNWuCbpnx49MuuYMSvIhkuc6dgyV2GzWiQkvublBYCCNHQpMm8NxzcP318OWXwZCcNKUuGhHJep07V3zJXQDy86FHj+C5ffuNiT7NqQUvIhLLypXQqxcceCAsXgxPPw1vvZURyR2U4EUky4Rd6bFM7sGBTZsGQx4vuywopnbqlJQlBiqLumhEJGvk5UG3brB6dfC+oCB4D+Xoopk3L0jo77wDublBEbVt24TEm2hqwYtI1hg4cGNyL7Z6dfB5XMU7tmoF06YF/ewff5yxyR3UgheRLFLhSU2vvBL0tS9cCH//ezBhaaedKju8pFMLXkSyRtiVHjdYtCiYpHTKKVCrVjB56YknsiK5gxK8iGS46KLqb7/BVlttur3USU3r1gWt9GbN4LXXguUGZsyAo45KTtBJoi4aEclYJYuqK1ZAjRpQty789FPQch80qESBdcqUYEz77Nlw6qlw//3BvxBZSAleRDJWaUXVdetg221h+fISOy9bBgMGwGOPBZn/P/+B009PUqSpoS4aEclYoYqqRUXw4IPB5KSnnoKrr4Y5c7I+uYMSvIhksLhF1Rkz4NBDg36cffcN3g8ZAttsk6QIU0sJXkTSUnTxtF694FHydayi6h0Df4W+fYMx7AsWwOOPB+u1t2iRih8lZdQHLyJpp7TiabGSrzcpqjZwnjxtHIff1Be+/z44ye23w447JvcHSBNK8CKSdkornsayoaj68TfBEgMj3oA2bWDCBDjooITGme6U4EUk7ZTndnpb8yddC4ZAyyFBf8199wV3Wqqu9KZvQETSTqzb7JV0HG/wAJexD9/AGefCPffArrsmPsAMoSKriKSN4sJqQUHZq/LuyhLGci5vcAKY8fbVb8DYsUruJagFLyJpoWRh1T1I8u5BERXglxXrGVB7BNf8cQM1fC1Dt7uFXYddRaeuNVMXeBpTgheRtFBaYdU9uIfqwoXARx8FSwx88QWceCKMGEH/vfZKRagZQ100IpIWYhVWVxX8FDTt27UL1h8YNw5efRWU3ONKWII3syZmNiPq8auZXZGo64lIZtt8VqrThcf4KqcJPPII9OsHc+dCx44Zddu8VEpYgnf3+e7ext3bAG2B1cALibqeiGSm0gqrLfiS9zmCx+hK0V77BHdYGjoU6tRJaayZJlldNMcAC9w9xMAnEakqigurxUMia/tv3MkAPmc/WubM4eNLHqL+vA+gdevUBpqhklVkPQ94JknXEpEMsbGw6pzBf7iPPjTkO57d5iLOXXgHB9erl+oQM1rCW/BmthVwGjAuxvZuZpZvZvnLli1LdDgikkYWLYLG/JeXOZUXOIuVbM+hfECn1Q8HK4rJFklGF81JwHR3/6G0je4+xt1z3T23fv36SQhHRJKhuG/dLFg1IPq5Xj3Yte4arvVBzKE5RzGZ/txNW6YxlUNj30NVyiUZXTSdUPeMSJVSctJSYeGmz61WvMNIetKU+YznLK7gXhbTAIhxD1WpkIS24M1sG+A4YEIiryMi6SXWapA7sZQnuYB3OIatWEsHXqEj4zck90aNYMyYEvdQlQpLaAve3X8H6ibyGiKSfkpOWsqhkO6MZhADqcUf3MK/GMy1/EmtDfuYRWasSqXRTFYRqXTRfehtyecTDuIBepFPLq2YyY3csklyL3mMVA4leBGpsNIKqfXqBSsKbMdKRnAZn3Igu7GETjzNcbzJVzTZ7Dzqd08MJXgRqZCSk5SKC6grVjhn/P4U82lCd0Yzgl40t3mMpRPVqgVTVevWDR5m6ndPJK0mKSIVUlohtQnzGElP2vMun3IAHXiV6bSlUUP4eWFKwqzS1IIXkQqJLqTWYjW3MZCZtGJ/ptODkRzCR0yn7Wb7SvIowYtIhRQXRU9mIrNpwUBuZyzn0YT5jKYHRVTbbF9JLiV4EdmkWJqTEzybQbVqpc9EzcmBooJFTOBMJnIqf1CLI5lMF57gR3ba5NwqoKaOErxIFVeyWOq+cVtRUfAcPRO1Ouu40u9kLs04gde5hsG0YQYf5BwJqICaTuIWWc1sL2Cxu68xs6OAVsAT7r4ysaGJSDLEmnVamsOYwih60JLZvMSpXM79FNAYgEYNNFEp3YRpwY8HCs1sb2AM0AB4OqFRiUjShCmA1mMZj3IhUziCOqziNF7kdF7akNzDnkeSK0yCL3L39cCZwHB3vwrYJbFhiUiylFUANYq4lDHMpwmdyWMIV9OcObzMaeU6j6RGmAS/zsw6AV2AiZHPaiQuJBFJhuhb5ZWmNTP4kEMZwz+ZSSta8wXXMoTVbLPZvlttpUJqOgqT4LsChwCD3P2/ZrYH8GRiwxKRRCpZWI1Wh18ZxhVMoy17sYB/8DjH5rzLXJpTLTLyMfqe13XrBvfEViE1/ZhHl8xj7WRWC2jo7vMTGUxubq7n5+cn8hIiQqyWu3MOzzGMvuzMUnK6/xNuvx122CEFEUpYZjbN3XNL2xa3BW9mpwIzgNci79uY2UuVGqGIJFXJgujefM1rnMiznMdSdqYdH8GoUUruGS5MF81NwIHASgB3nwHsmbCIRCThiguiW/MnN3ITs9iXQ/iIy7mPA/mUpY0OSm2AUilCFVnd/ZcSnxUlIhgRqVx5ecHyvcUzU4sfBQVwPK/zJS25iZt5gTNpwnyGczlb166ugmmWCJPgZ5vZ+UA1M9vHzIYDUxMcl4hsobw86NoVVqzY9PNdWcKznMPrnEgRORzHG1yQ8wxL2UUzT7NMmATfG2gBrCG4efavwBUJjElEKsHAgbBu3cb31VjPFQxjHk05jZf4F7ewL7N4i+No0CBYomDhQiX3bBJ3qQJ3Xw0MjDxEJENEF1IP5iNG0YM2fMEkTqQXI/iWvUrdV7JHzARvZi8DMcdQuvvmU9lEJG00bAirClYwhGu4lIdYzG6czfNM4CzANttXsk9ZLfi7kxaFiJRLXh706bN5/3oxo4guPM6dDGAHfmYo/biJm/iNOpvtq1mo2Stmgnf395IZiIiEU1w8je5fj9aCLxlFDw7nA6ZyCN0ZzSxalbpv3bpw333qd89WZXXRPOfu55jZLErpqnH30v+PEZGEKlk8LbYNv3EjN9OXYfzCdlzMQzxKVzwylqJRIy3nW9WU1UXTJ/J8SjICEZFwNi+IOmfwH+6jDw35joe4mGsYwgrqxTlOsl3MYZLu/n3kZU93L4h+AD2TE55I1RFrUlLJR/TyUXvwLRM5hRc4i5Vsz6F8wKU8tFlyBxVSq6Iw4+CPK+Wzkyo7EJGqLNakpFi2Yg3XMYjZtOBI3qMfQ2nLNKZyaOn7q5BaJZXVB9+DoKW+p5nNjNpUB/gw0YGJVCWx+tVLczTvMJKeNGU+z3M2V3AvS9g95v4qpFZdZfXBPw1MAgYD10R9vsrdf0poVCJVTJj+8Z1YylD605mnWcCenMSrvBb5Y9ps4w2yRYqV1Qf/i7svdPdOwGJgHcFomm3NTL15IpWorP7xHArpyQPMoykdeZ5b+Bct+XJDco93vFRdcZcqMLNeBEsG/8DGVSQdYgysFZFQ4k1WAsjlM0bRg1ym8RbH0JORfM1fN9lH/esSS9wET7CwWBN3D1n+EZF44k1W2o6V3M51dGc0P7AT5/EMz3IuJZcYUP+6lCVMgv8OKLkevIhsgdhFVaczeQylP/VYTk7vXuxy662M3W47xiY7SMl4YRL8t8BkM3uFYMlgANz9noRFJZLlSiuqNmUuI+nJ0UzmEw6kA5OYdv/+yQ9OskaYcfCLgDeBrQiGSBY/RKSCoouitVjNIK7jC1rThhl0ZxTtmMqKRkrusmXCrAd/czICEclG8QqpJzOR4fRmDxbyOP9gAHfyIzupcCqVIswomvrAAIK7OtUs/tzd2ycwLpGMV1YhtQGLuI8+nMl/mEMzjmQy73MkoMKpVJ4wffB5wLMEi451B7oAyxIZlEg2KK2QWp119GUYN3IzhnM1QxhGX3ZttBW+MCVhShYLk+DruvvDZtYnskb8e2b2WaIDE8l0JQuph/M+o+hBC+bwIqdxOfeziEal7itSGcIUWYvbIN+b2clmth+wYwJjEskKxYXUeizjUS7kfY5kW37jNF7kDF7ckNyj9xWpTGES/G1mth3QH7gSeAjoG+bkZra9mT1vZvPMbK6ZHbIFsYqkpVjL/C4qKKIb/2Y+TehMHoO5hubM4WU2vZ2xCqqSKGFG0UyMvPwFOLqc578PeM3dO5rZVkDtch4vktZiFVLb8Dmj6MHBfMJkjqQnI5lL882OV0FVEinMKJpHKf2WfRfFOW474Ajgwsj+a4G1FYpSJE2VLKTW4Vdu4QZ6M5wV1OXvPMFTXEDxEgO6bZ4kU5gi68So1zWBM4H/hThuD4LRNo+aWWtgGtDH3X+P3snMugHdABqqI1IyzMbiqHMOzzGMvuzMUv7NP7mO21nJDjH2F0m8uH3w7j4+6pEHnAPkhjh3dWB/YJS77wf8zqbryheff4y757p7bv369csZvkhqNWwIe/M1r3MCz3Ie37MLB/MxPRm1WXIv3l8kWcIUWUvaB/hLiP0WA4vd/ZPI++cJEr5IxsvLg93q/knXghv5kpYcxCf05n4O5FM+48BSj1ExVZItTB/8KoI+eIs8LwWujnecuy81s+/MrIm7zweOAeZsYbwiKZeXB093eZ33Ci9jbxbwNJ3oz1CWskvMY1RMlVQIM4pmSxYW6w3kRUbQfAt03YJziaTekiVs3+0KXil8nvn8lWN5k7c5dpNdVEiVdFFmgjezWkBn2DC+Kx94PjIiJi53n0G4/nqR9LZ+PQwfDjfcQPvV67meW7mLq1jL1pvtqkKqpIuYffBmti9Bl8rhwMLI4wTgw8gEptuSEaBIKkRPXmpnU/miRlvo149XfzucFsxmENeXmtxBhVRJH2W14O8Hurn7m9EfmtmxwJfA7EQGJpIqxZOX6qxbwRiu4VIeYjG7cTbPM4GzKHnbvGgqpEo6KWsUzS4lkzuAu79FsD7NmQmLSiSFrr+uiAvWPcJ8mtCVR7mb/jRjLhM4m7KSe9268MgjKqRK+iirBZ9jZlu7+5roD82sJrDO3VcnNjSRFJg1iycX9eAwPuRD2tGDUcyiVdzDzGD58iTEJ1IOZbXgnwDGm9mGJe/MrDHwHPBkguMSSa7ffoOrroL99qN5zjwu4mEOZ0qo5A7qd5f0FDPBu/ttwGvAFDNbbmbLgfeAN9391mQFKJIIG4uozlk2ge/qNIO77+bBwq7sUzSfR7kIDzkPUP3ukq7KHCbp7iOAEWZWJ/J+VVKiEkmg4iLq7uu+5XF6czKv8gWtOJdn+Yh25TqXJjBJOguz2JgSu2SVm69bw4B1dzGQQaynOv0Yyv1cTmEZvw6avCSZKFSCF8kab7/NS4suoynzGUdH+jKMJewe9zBNXpJMVJHFxkQyz9KlcP75cOyx1Kq+jpN4lXMYFyq5g4qokpniJngzq21m/zKzByPv9zGzUxIfmsiWycuDv9QtpJeN4JddmrDmmfHczA00Xf8lr3FS6POoiCqZKkwXzaMEN+sovp/qEmAcm94IRCSt5OXBiC6fMamwO22Zzpscy2U8wNf8tVznURFVMlmYBL+Xu59rZp0A3H21mcWezieSaj//TFH3gXxYOJql7My5jOU5zqGsWagqoko2CtMHvzayqqQDmNlewJqyDxFJAXd48klo2pTzf/s3w+lNM+byHOdSVnIHFVElO4Vpwd9IMOGpgZnlAYcSuZG2SNqYOxd69oTJk+HAAzktZxKvLg1/AzEVUSUbhbkn65vAWQRJ/Rkg190nJzYskfjy8qBB3dXcbtextnlrfp48g38ymmqfTi1Xcq9dW0VUyU4xW/BmVvI35PvIc0Mza+ju0xMXlkjZ8vLg+S4vM6WwN40p4DG6MIA7WRbqdsGQkwNFRUHf+6BBKqJKdiqri2ZoGdscaF/JsYiEU1BA/Uv78ELhi8ymOUfwHlM4Iu5hKqRKVRMzwbv70ckMRCSutWth2DC45RYO/QOuZgjD6Ms6tgp1uAqpUtXELbJG1n/vCRxG0HKfAox29z8THJvIRu+9FxRR58yB00/n+Pz7mLqkUfzjoqiQKlVNmGGSTwAtgOHAiMhrrQcvSfH8yB8ZW7MLHHUUC+f8zqm8hL34n3Ind81GlaoozDDJlu7ePOr9u2Y2J1EBiQBQVMQnlzxI+0evZVt+43auZRADWc025T6VZqNKVRUmwU83s4Pd/WMAMzsIyE9sWFKlff45dO/OQZ9+yrscRU9GMo9mcQ9TEVVkU2G6aNoCU81soZktBD4CDjCzWWY2M6HRSdXy66/Qpw/k5sLChfydJ2nPO6GSO6iIKlJSmBb8iQmPQqo2d3j2WejXL1jWt3t3GDSIKfvtAAXhT6MiqsimwsxkLQB+BbYD6hY/3L0gsk2k4r76Co4/Hjp1gl12gY8/hpEjYYcd6NAh/GlURBXZXJhhkrcSLFOwgMiCY2iik2ypP/6AwYPhjjugZk0YPhx69IBq1YBgpurjj4c7lYqoIqUL00VzDsGSwWsTHYxUEa+9Br16wYIFwV2W7r47aL1HGTgQVq/e/FAVUkXCC1Nk/RLYPsFxSFWwZAn87W9w0klBS/2tt4KmeonkDrELpiqkioQXJsEPBj43s9fN7KXiR6IDkyyyfj3ccw80bQoTJ8Ktt8LMmXDMMRt2ycuDevXALHi4l34qFVJFwgvTRfM4cAcwCyhKbDiSdaZODfrWZ86EDh2CvvY999xkl7w86NoV1q0r+1QqpIqUT5gEv9rd7094JJJdVqyAq6+Ghx+G3XeH8ePhzDOD5nkJAwfGT+4AdeqokCpSHmES/BQzGwy8RNSt+rQevJSqqAgeewwGDICVK6F/f7jpJth225iHhO1X/+mnyghQpOoIk+D3izwfHPWZhknK5mbNCrpjPvwQDj0URo2CffeNe1jDhlAQYkaF+t9Fyidugte68BLXb78FrfR774Xtt+ejSx/h/Ne7sLBVTpkF0/LQbfVEyi9MCx4zO5lgmeCaxZ+5+y2JCkoyhDtMmABXXAGLF8MllzCu7RAu7F93wxj2LUnuuq2eyJYJM5N1NFAbOBp4COgIfJrguCTdffttMFlp0iRo1SpYS6ZdO65qXPoEpfLQZCaRyhFmHHw7d/8H8LO73wwcAvw1sWFJ2lqzJhjH3qIFTJkSjG+fNg3atQMqZyKSJjOJVI4wCf6PyPNqM9sVWAdsPvVQst/bbwet9RtugFNOgblzoW9fqL7xD8HKKISqmCpSOcIk+Ilmtj1wFzAdWAg8HebkkTXkZ5nZDDPTTUIyRF4eNG4cDFmvXh12se95Jud8OPZYvvmqkBOZhD0/Dmuw+4aZp9WqBc9hRsOURZOZRCpPmFE0t0ZejjeziUBNd/+lHNc42t2XVyg6Sbq8POjWLehHz6GQHoUjuY3rqel/cjM3MIRr+JNamx1XVAlznLUqpEjlipngzewA4Dt3Xxp5/w/gbKDAzG5yd007yULFqzgewKeMogdtmc4bHMdlPMA37FOhc6poKpIaZXXR/BtYC2BmRwBDgCeAX4AxIc/vwBtmNs3MupW2g5l1M7N8M8tftmxZ+MglIX4t+JmR9OBjDmYXvudcxnICr1c4uYOKpiKpUlYXTbWoVvq5wBh3H0/QVTMj5PkPc/clZvYX4E0zm+fu70fv4O5jiPyDkZubWwlTYqRC3OGpp5ifcyU7Fi3nfi7nBm5hFf+3xadW0VQkNcpqwVczs+J/AI4B3onaFmqClLsviTz/CLwAHFiRIGXLlCyaRj/Xqwfttp/D5Jyj4R//YEHRHuSST1/urZTkrqKpSOqUleCfAd4zsxcJhkpOATCzvQm6acpkZtuYWZ3i18DxBDcPkSQqLpoWj24pLNz4XIvV9F9xLe/90ppWzKQb/6YdU5mxYfmhYDYpbLiTXmmLQW6yX/T2unXhkUdUNBVJlZgtcXcfZGZvE4x5f8N9w6TzHKB3iHPvBLxgwW98deBpd39tC+OVcop167tTeJnh9KYxBTxGFwZwJ8v4y2b7NWigAqlIpiqzq8XdPy7ls6/CnNjdvwVaVzAuqSQlC5wNKeB+Lud0XmI2zTmC95jCEaGPF5HMEWaik2Sw4gJnDdZyNUOYSzOO5S0GcAdtmFFmco8+XkQyjxJ8hikumObkBAXSevU2fV2ygLp8ORzBe3zOfgzhWt7geJozh7sYwHpqlHktFUhFMluo0TCSHqJnmUJwV7xi0a+LC6k5K37kAa6iC0+wkEacyku8mnMqRUVB0bSwMCiEFh8fvXa7ZpWKZD4l+AwSq2BaklFEN8YwmGvZht+5nWu5jev5g9o0UtFUpMpQgs8gYQqebfic0XTnID7lXY6iJyOZR7NynUNEsoP64NNUaX3tZd0d6f/4hfu4nHxyacxCLuBJ2vPOJskdVDQVqUrUgk9DZfW1b845l2cZRl924gdG0YPruY2V7LDZnrqvqUjVohZ8Ggrb137g9l/xbo3jGUsnfqi2Gyds9wm9eIBV1YLkXrdu8DALVnQcM0ZFU5GqRC34NBSvn7wmf3Adg/nX6jugVk24ZzhtevTgzeL1BEREUIJPSw0bxr4z0olMYgS92ItvoeP5MHQo7LxzcgMUkYygLpoEiS6SNm4cvC/5Wc+epb8vKNh8Ua/dWMw4OjKJDqy3Grx17dvBCZXcRSQG87KGZiRZbm6u5+dn/q1bSxZJAWrUCJL22rXhz2MG1Xwd19QeztWrb6Qa6xmx/fXsPuxKOl24deUHLiIZx8ymuXtuadvURZMApRVJ160r/3kO8Q95qEYPmq2eBR06wPDhXLXnnpUTpIhkPXXRJMCWTiaqy3Ie5BI+5DC2XfczTJgAEyeCkruIlIMSfAJUdDKRUcRFPMw8mnIhj3EXV3JCg7lw5pmx77QhIhKDEnwlKFk87dAhmFQUrUaNYHXGWPZlJlM4nIe5hLk0Yz8+56badzFw8LaJDF1EspgS/BaKviWee/D8+OPQpUswuah4ktGjjwa3r4v+rEcPaN5gFUPpz3T2p3XN+VxV9xGO4j1WNdpXE5NEZItoFM0WKh7WWFKjRnFWbXQP+tb79IElS+DSS2Hw4I3r94qIhFDWKBq14LdQrIJqmYXWBQuCfpyOHYNVxKZODdYRUHIXkUqkBL+FYhVUS/18zRq49VZo2RI++ADuuQfy8+GQQxIao4hUTVmf4EubUVqR/WJtHzRo84Jqqas2vvUW7Lsv3HADnHoqzJsHffsG99cTEUkEd0+bR9u2bb0yPfWUe+3a7kGHd/CoXTv4vDz7hdneqJG7WfC8yfn/9z/3884LDtprL/dJkyr1ZxSRqg3I9xg5NauLrGELoPH2q1AhtbAQRo6E66+HP/+Ea6+Fa66BmjXL+VOIiMRWZZcqCFsAjbdfuQupn34K3bvD55/DccfBAw/APvvEjVdEpDJldR982AJovP1CF1J//jlI7AcfDEuXwrPPwuuvK7mLSEqkdYIPWyCNJWwBNN5+cc/jDk88AU2awIMPwuWXB0XUc87REgMikjqxOudT8YgusoYtkMZTZgG0HPvF3D57tvuRRwYBHnSQ+/Tp5QtQRGQLkIlF1grPEE2W338PxrQPHQp16sCQIXDJJcGfGyIiSZKRRdYKzRBNlpdeCrphCgrgwgvhzjuhfv1URyUisom0bW6Wa4ZosixcCKefHjy23Rbefz9YRUzJXUTSUNom+NAzRJNh7dqgC6Z582BG6p13BkMgDz88BcGIiISTtgm+c+dg/a3o5XVTsnzu5MnQpk0wUemEE2DuXLjqqmCBdxGRNJa2ffAQJPOUrYf+449w5ZXw5JNBxffll+GUU1IUjIhI+aVtCz5lCgth9OhgTPvYsXDddTB7tpK7iGSctG7BJ9306cFtlj79FI4+OlhioFmzVEclIlIhasED/PJLMOzxgAOCkTJPPQVvv63kLiIZrWq34N2Dbph+/eCHH4LW+6BBsP32qY5MRGSLVd0EP38+XHZZ0FJv2zaYvHTAAamOSkSk0lS9Lpo//oB//QtatYLPPoMRI+CTT5TcRSTrJLwFb2bVgHxgibundijKpEnQqxd8+20w/vLuu2HnnVMakohIoiSjBd8HmJuE68T23XfQsSN06BBMUHr77aCQquQuIlksoQnezHYHTgYeSuR1Ylq3LljtsVkzeOWVoID6xRfQvn1KwhERSaZEd9HcCwwA6sTawcy6Ad0AGlbmSmIffhiMipk1C04+GYYPhz32qLzzi4ikuYS14M3sFOBHd59W1n7uPsbdc909t35lrMq4fDlcfDEcdlhwC70JE4JlBpTcRaSKSWQXzaHAaWa2EBgLtDezpxJ2taIiePjhYImBJ54IFgSbOxfOPFO3zRORKilhCd7dr3X33d29MXAe8I67X5CQi82cGSzde8klwZK+n38eLOm77bYJuZyISCbI7HHwq1ZB//6w//7w1VfBzTfefx9atkx1ZCIiKZeUmazuPhmYXIknhPHj4YorYMkSuPRSGDwY6tattEuIiGS6zGvBL1gQjGf/29+gXj346KPgTiBK7iIim8icBL9mDdxyC7RoAR98AMOGQX4+HHxwqiMTEUlLmbHY2FtvQc+e8PXXQct92DDYbbdURyUiktbSuwXvDhdeCMcdF7x+7TV47jkldxGRENI7wZvB3nvDjTcGM1JPOCHVEYmIZIz076K5/vpURyAikpHSuwUvIiIVpgQvIpKllOBFRLKUEryISJZSghcRyVJK8CIiWUoJXkQkSynBi4hkKXP3VMewgZktAwpSHUcJ9YDlqQ4ixfQd6DsAfQeQnt9BI3cv9X6naZXg05GZ5bt7bqrjSCV9B/oOQN8BZN53oC4aEZEspQQvIpKllODjG5PqANKAvgN9B6DvADLsO1AfvIhIllILXkQkSynBi4hkKSX4EMzsLjObZ2YzzewFM9s+1TElm5n9zcxmm1mRmWXMMLEtZWYnmtl8M/vGzK5JdTypYGaPmNmPZvZlqmNJBTNrYGbvmtmcyO9An1THFJYSfDhvAi3dvRXwFXBtiuNJhS+Bs4D3Ux1IsphZNeAB4CSgOdDJzJqnNqqUeAw4MdVBpNB6oL+7NwcOBi7LlP8PlOBDcPc33H195O3HwO6pjCcV3H2uu89PdRxJdiDwjbt/6+5rgbHA6SmOKenc/X3gp1THkSru/r27T4+8XgXMBXZLbVThKMGX30XApFQHIUmxG/Bd1PvFZMgvtiSGmTUG9gM+SXEooaT/TbeTxMzeAnYuZdNAd38xss9Agj/X8pIZW7KE+Q5Eqioz2xYYD1zh7r+mOp4wlOAj3P3Ysrab2YXAKcAxnqWTB+J9B1XQEqBB1PvdI59JFWNmNQiSe567T0h1PGGpiyYEMzsRGACc5u6rUx2PJM1nwD5mtoeZbQWcB7yU4pgkyczMgIeBue5+T6rjKQ8l+HBGAHWAN81shpmNTnVAyWZmZ5rZYuAQ4BUzez3VMSVapLDeC3idoLD2nLvPTm1UyWdmzwAfAU3MbLGZXZzqmJLsUODvQPvI7/8MM+uQ6qDC0FIFIiJZSi14EZEspQQvIpKllOBFRLKUEryISJZSghcRyVJK8FLpzKxu1HCypWa2JPJ6pZnNSXIsZ0QvDGVmt5hZuSd0mVnjWKspmlkLM3snsurkAjO72cwq/XerrJ/FzCZXpVU+JRwleKl07r7C3du4extgNDAs8roNUFTZ1zOzsmZkn0GwEmRxbDe4+1uVeO1aBJOfhrh7E2BfgkXKErGk7Bkk8GeR7KMEL8lWzcwejKyr/UYkQWJme5nZa2Y2zcymmFnTyOeNI63jmWb2tpk1jHz+mJmNNrNPgDtLO97M2gGnAXdF/oLYK3Jcx8g5DjCzqWb2hZl9amZ1ItebYmbTI492cX6e84EP3f0NgMhM517AVZFr3GRmVxbvbGZfRhaswsz+E4l3tpl1i9rnNzMbFInrYzPbKd7PEs3MjjezjyLxj4usoYKZDYmsaT7TzO4u/386yTRK8JJs+wAPuHsLYCVwduTzMUBvd28LXAmMjHw+HHg8shZ/HnB/1Ll2B9q5e7/Sjnf3qQSt66sif1EsKD4wsvTAs0Afd28NHAv8AfwIHOfu+wPnlrheaVoA06I/iFynlsW/McxFkXhzgcvNrG7k822AjyNxvQ9cWtbPEs3M6gHXA8dGfoZ8oF/k3GcCLSLf5W1xYpMsoMXGJNn+6+4zIq+nAY0jLcx2wLhg2Q8Ato48H0JwoxGAJ4E7o841zt0L4xwfSxPge3f/DKB4dUAz2wYYYWZtgELgr+X9AcvhcjM7M/K6AcE/fiuAtcDEyOfTgOPKcc6DCbpxPox8F1sRLDPwC/An8LCZTYw6v2QxJXhJtjVRrwuBWgR/Sa6M9NOXx++R54oeX5q+wA9A68h5/4yz/xzgiOgPzGxPYIW7rzSz9Wz6l3LNyD5HEfzVcIi7rzazycXbgHVRK5YWUr7fUwPedPdOm20wOxA4BuhI0I3UvhznlQykLhpJuUjr+b9m9jcIVu8zs9aRzVMJVnEE6AxMKefxqwgWiitpPrCLmR0QOaZOpFi7HUHLvohggalqccLPAw6LGs1Si6Bb58bI9oXA/pFt+wN7RD7fDvg5ktybErS844n1s0T7GDjUzPaOXHMbM/tr5K+c7dz9VYJ/xFqXdRLJDkrwki46Axeb2RfAbDbeGq830NXMZhIk3FijU2IdPxa4ysw+N7O9ineO3ILvXGB45Jg3CVrQI4Eukc+asvGvhFK5+x8Exc+BZvYVsJyg6Fp8U5jxwI5mNpug1fxV5PPXgOpmNhcYQpCY4yn1ZykRzzLgQuCZyHf2UeTnqANMjHz2AdAvxPUkw2k1SZFKZGZnAPcAR7t7QYrDkSpOCV5EJEupi0ZEJEspwYuIZCkleBGRLKUELyKSpZTgRUSylBK8iEiW+n+0RYw3pwH6BAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "from statsmodels.graphics.gofplots import qqplot\n",
    "\n",
    "# q-q plot\n",
    "qqplot(df_iris['Sepal.Length'], line='s')\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 지수분포 (Exponential Distribution)\n",
    "\n",
    "어떤 사건이 발생하는 간격(시간)이 따르는 분포\n",
    "\n",
    "**확률밀도함수**\n",
    "\n",
    "단위 시간당 평균 $\\lambda$번 발생하는 사건의 발생 간격을 따를 때, \n",
    "\n",
    "$$f(x) = \\lambda e^{-\\lambda x} \\quad (x \\geq 0)$$\n",
    "\n",
    "**기대값과 분산**\n",
    "\n",
    "$$E(X) = \\frac{1}{\\lambda} \\quad V(X) = \\frac{1}{\\lambda^2}$$\n",
    "\n",
    "\n",
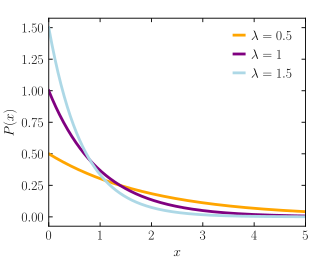    "![](https://upload.wikimedia.org/wikipedia/commons/thumb/0/02/Exponential_probability_density.svg/325px-Exponential_probability_density.svg.png)\n",
    "\n",
    "https://en.wikipedia.org/wiki/Exponential_distribution\n",
    "\n",
    "**Further Reading**\n",
    "* [Exponential distribution](https://en.wikipedia.org/wiki/Exponential_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 17,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "f(1)=0.271, f(3)=0.005\n",
      "F(1)=0.865, F(3)=0.998\n",
      "E(X)=0.500, V(X)=0.250\n"
     ]
    },
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 17,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEGCAYAAABo25JHAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAmO0lEQVR4nO3debSkdX3n8fe3trvfXm93X3pnbYmCYoPOqBGNJkAS0MQkEk1GR2UWzcSJyUhmctQxJ3Pi5IxZJhpDDCESlRCTmJ6IQVSUHJClAUW2hobG3jeavvut9Tt/PE91F5e7VN2up56nbn1e59Shqp6nqr51Of1867d9f+buiIhI50rFHYCIiMRLiUBEpMMpEYiIdDglAhGRDqdEICLS4TJxB9Co1atX+5YtW+IOQ0SkrTz44IPH3X1otmNtlwi2bNnCzp074w5DRKStmNmP5jqmriERkQ6nRCAi0uGUCEREOpwSgYhIh1MiEBHpcEoEIiIdTolARKTDKRE0icp5i0i7UiJogrsPT/LZx15gtFCOOxQRkYYpEZyhew5P8q+HJhkrVrjv6FTc4YiINEyJ4AyU3bn78CTnL8vx8pVd/OD4NBPFStxhiYg0RIngDByfKlN22La8i3+7tpeyw85jahWISHtRIjgDR6ZKAKztTbOyO82m/iy7RwoxRyUi0pjIEoGZ3WhmR83s0QXOu9TMSmb2jqhiicqRqRK5lLGyKw3A5oEsx6bLTJbUPSQi7SPKFsFNwBXznWBmaeBTwDcijCMyRyZLrOlJY2YAbOrPArB3vBhnWCIiDYksEbj7XcCJBU77NeDvgaNRxRGVijtHpkqs7T29pcNwX4ZsCvaOKRGISPuIbYzAzNYDbwf+LK4YzsQL+TLFCqzrOZ0I0mZs6MuqRSAibSXOweI/Aj7q7gt2qJvZdWa208x2Hjt2LPrI6nBkMlg8VtsigKB76Ph0WdNIRaRtxJkItgO3mNlzwDuAz5rZ22Y70d1vcPft7r59aGjWLTdb7kQ+SASrwoHiqg3hOMHBSbUKRKQ9xLZnsbtvrd43s5uAf3b3r8YVT6PGixV6M0Y6ZS96fm1PBgMOT5Y4b1lXPMGJiDQgskRgZl8GLgdWm9l+4ONAFsDdPxfV57bKWLFMf/alDapc2ljVnebwZCmGqEREGhdZInD3axs49z1RxRGV8WKFgVkSAcC63gzPjhZw91NTS0VEkkorixdpvFiZtUUAMNybYbLkjGnAWETagBLBIlTcmSj5nIlgXTiT6JC6h0SkDSgRLEJ1auhciWBNOGB8RIlARNqAEsEijC+QCLIpY6gnrRaBiLQFJYJFGC/Nnwgg6B46PFnSFpYiknhKBIuwUIsAgtITU2VnpKABYxFJNiWCRRgrVjCgLzP3n284HDDWegIRSTolgkUYL1boy6RIzbNGYKgnQ8qUCEQk+ZQIFmG+NQRVmZQx1K0BYxFJPiWCRagnEQAM92Y5PKUBYxFJNiWCRag3EazrzZAvOyc1YCwiCaZE0KCKO5Mlpy+7cA0hrTAWkXagRNCgfDno5ulOL/ynG+pOk9aAsYgknBJBg6ZKQSLoySzcIkinjDU9GQ5pkxoRSTAlggZNl4P+/npaBBCsJzgyWdaAsYgklhJBg6bL9bcIIBgnKFT81NaWIiJJo0TQoKlStUVQXyIY1oCxiCScEkGDphsYLAZY1Z0mm1IiEJHkUiJoUHWwuLvOrqGUGWt7Mpo5JCKJpUTQoOlyhVzKSDewF/G63gxHJktUNGAsIgkUWSIwsxvN7KiZPTrH8XeZ2SNm9kMzu8fMLo4qlmaaLnvdrYGq4d4MJYfj0xowFpHkibJFcBNwxTzH9wBvdPdXAL8L3BBhLE0zVarQU+dAcdU6laQWkQSLLBG4+13AiXmO3+PuL4QP7wU2RBVLM02Xve6B4qqVXWlyKdOAsYgkUlLGCN4HfH2ug2Z2nZntNLOdx44da2FYLzVdarxryMxObV0pIpI0sScCM3sTQSL46FznuPsN7r7d3bcPDQ21LrhZTJUr9DTYIoBgnODoVIlyRQPGIpIssSYCM7sI+Dxwjbs/H2cs9XD3RbUIIBgnKDsc04CxiCRMbInAzDYB/wD8irs/FVccjShWoAINDxaD9jAWkeTKRPXGZvZl4HJgtZntBz4OZAHc/XPAx4BVwGctmJNfcvftUcXTDFMNFpyrtSyXojttHJos8kq6mx2aiMiiRZYI3P3aBY6/H3h/VJ8fhekGVxXXqg4Ya+aQiCRN7IPF7eR0i6DxRABB99DxqTJFDRiLSIIoETRg+tSmNIv7s63rzVABjk2pVSAiyaFE0IDTlUcX3yIAVSIVkWRRImhAo7uTzTSQTdGbMc0cEpFEUSJowHTJSQHZRf7VzIxhDRiLSMIoETQgX3G60oY1UIJ6puHeLMeny+TD1oWISNyUCBpQKDu5RY4PVJ3Vp4VlIpIsSgQNqLYIzoQGjEUkaZQIGlAoO7nUmSWCnkyKFV0pDk4oEYhIMigRNCBfrpxxiwCCcQK1CEQkKZQIGlCoOF2LnDpa66zeDGPFCmMFVSIVkfgpETQg34SuIYDhcMD4oFoFIpIASgQNKJTPfLAYYG1PhpTBIY0TiEgCKBHUqVxxSs4ZTx8FyKSMNT0ZtQhEJBGUCOpUCCuGNqNrCIJxgsOTJSquSqQiEi8lgjrlw4JzzegagmA9QaHiPK+tK0UkZkoEdTrVImhSIjhLA8YikhBKBHU61SJoUtfQyq40XWnTgLGIxE6JoE6FJncNna5EWmzK+4mILFZkicDMbjSzo2b26BzHzcz+xMx2m9kjZnZJVLE0Q77JXUMQDBgf1daVIhKzKFsENwFXzHP8SuC88HYd8GcRxnLGCk3uGoJgYZkDRzROICIxiiwRuPtdwIl5TrkG+IIH7gWWm9lwVPGcqer+Ac1sEQz3ZgENGItIvOIcI1gP7Kt5vD98LpHyTV5HANCfTTGYTXFoQuMEIhKfthgsNrPrzGynme08duxYLDEUyk5X6sx2J5vNcJ9WGItIvOJMBAeAjTWPN4TPvYS73+Du2919+9DQUEuCmynfhN3JZnNWb4aRQoWJorauFJF4xJkIdgC/Gs4eei0w4u6HYoxnXoVKNIlguC8YJ9D+BCISl0xUb2xmXwYuB1ab2X7g40AWwN0/B9wGXAXsBiaB90YVSzNUu4aabV1PhhRwYKLIuctyTX9/EZGFRJYI3P3aBY478MGoPr/ZouoayqWNdb0Z9o1rwFhE4tEWg8VJUGjCxvVz2dAfbF1Z0sIyEYmBEkGdmrU72Ww29mcou9YTiEg8lAjq1KzdyWazIRwwVveQiMRBiaAO7k4+ollDAD2ZFEPdafYrEYhIDJQI6lDdiyCKWUNVG/uzHJjQjmUi0np1JQIze0XUgSTZ6RLU0eXNDf1ZChXnyJTGCUSkteq9sn3WzO43s/9sZssijSiBoihBPdPGcMeyfeNKBCLSWnUlAnd/A/AugpIQD5rZl8zsrZFGliBRlKCeaSCXZnkupXECEWm5uvs63P1p4HeAjwJvBP7EzJ40s5+LKrikqCaCKFsEEHQP7Zso4honEJEWqneM4CIz+0PgCeDNwM+6+8vC+38YYXyJEEUJ6tls7M8yVXKez5cj/RwRkVr1tgj+L/AQcLG7f9DdHwJw94MErYQlLd/k/YrnslHrCUQkBvXWGvppYMrdywBmlgK63X3S3W+OLLqEaPbG9XNZ0ZViIJviubEir1rdE+lniYhU1dsi+CZQe2XqDZ/rCK3qGjIztg5keW6sqPUEItIy9SaCbncfrz4I7/dGE1LyFMpOxiAdcSIA2DqYI1927U8gIi1TbyKYMLNLqg/M7NXAVDQhJU9UJahns2UgGCfYM6pxAhFpjXrHCD4M/J2ZHQQMWAf8UlRBJU2UJahn6smkGO7NsGeswOuHO6bRJSIxqisRuPsDZrYNuCB8ape7d8xP1ny5Evn4QK2tg1m+d3iK6VKF7ozKQYlItBq5ylwKXARcAlxrZr8aTUjJky97pHWGZto6kMOB5zSNVERaoK4WgZndDJwDfB+ornZy4AvRhJUshYozmGtdIjirL0NXytgzWmDb8q6Wfa6IdKZ6xwi2Axd6h9Y+iGrj+rmkzdg8kGXPWFBuwqx1ny0inafen7mPEgwQN8TMrjCzXWa228yun+X4JjO708weNrNHzOyqRj+jFaLclGYuWwezjBYqnFC5CRGJWL0tgtXA42Z2P5CvPunuV8/1AjNLA58B3grsBx4wsx3u/njNab8D3Oruf2ZmFwK3AVsa+wrRa3WLAIJxAphgz2iRVd31/m8SEWlcvVeYTyzivS8Ddrv7swBmdgtwDVCbCBwYDO8vAw4u4nMiVao4ZY++8uhMy7vSrOxK88xoge1rVG5CRKJT7/TR75rZZuA8d/+mmfUC6QVeth7YV/N4P/CaGed8AviGmf0a0Ae8ZbY3MrPrgOsANm3aVE/ITdOqOkOzOWcwy0PHpym0cEGbiHSeestQfwD4CvDn4VPrga824fOvBW5y9w3AVcDNYUG7F3H3G9x9u7tvHxoaasLH1q9VdYZmc+6yHGWH58YKLf9sEekc9Q4WfxB4HTAKpzapWbPAaw4Q7GhWtSF8rtb7gFvD9/we0E0wHpEYrSpBPZsN/Vm6UsbuUSUCEYlOvYkg7+6nrkZmliHo35/PA8B5ZrbVzHLAO4EdM87ZC/xE+J4vI0gEx+qMqSVatTvZbNJmbB3M8sxIQbuWiUhk6k0E3zWz/w70hHsV/x3w/+Z7gbuXgA8BtxPsbHaruz9mZp80s+pso48AHzCzHwBfBt6TtLUK+UoFiKdFAEH30ETJOTylaqQiEo16Zw1dT9CN80PgPxBM8/z8Qi9y99vCc2uf+1jN/ccJupwS6/TG9fHU/Dl7MAfA7pECw73ZWGIQkaWt3llDFeAvwltHKVTi6xoC6M2kWN+X4ZmRIm8YjiUEEVni6q01tIdZxgTc/eymR5QwcQ4WV507mOO7hyYZK5YZyC40a1dEpDGN1Bqq6gZ+AVjZ/HCSp1B2DMjEOI3/nGVBInh2pMjFq5UIRKS56ur4dvfna24H3P2PCDa0X/KqdYbiLPw21J1mMJvSNFIRiUS9XUOX1DxMEbQQOqIATj6GOkMzmRnnLsvxwxPTlCpOJuZ4RGRpqfdi/n9q7peA54BfbHo0CVQot26byvmcM5jjoePT7B0vnppJJCLSDPXOGnpT1IEkVSs3rp/P5oEs2VQwjVSJQESaqd6uod+Y77i7f7o54SRPoeL0JCARZFLG5oEcu0cLvFWb1YhIE9W7Smo78J8Iis2tB/4jwd7FA+FtyUpKiwCCaaSjhQrHp7VZjYg0T71jBBuAS9x9DMDMPgF8zd3fHVVgSVGoJGOMAIKy1BB0Dw31dMRYvYi0QL0tgrVA7dzFQvjcklcoeywlqGczkEuztifYrEZEpFnq/Vn5BeB+M/vH8PHbgL+OJKIEqbiHLYJ46gzN5txlOe45PMVUqUJPJjlxiUj7qndB2e8B7wVeCG/vdff/FWVgSRB3naHZnDuYw4Fn1SoQkSZp5CdlLzDq7n8M7DezrRHFlBinK48mJxGs683QlzF2jygRiEhz1LtV5ceBjwK/HT6VBf4mqqCSIh/jpjRzMTPOGczx7FiRcrK2bhCRNlVvi+DtwNXABIC7H2SJTxuF011DSZk1VHXOshz5snNgXJvViMiZqzcRFMKdwxzAzPqiCyk5TrUIEtQ1BLBlIEvaUBE6EWmKehPBrWb258ByM/sA8E06YJOaQgL2IphNVzrFpv5gL2MRkTO14PRRC2oZ/C2wDRgFLgA+5u53RBxb7PIJnDVUdc6yHN/cP8EL+TIrurRHgYgs3oItgrBL6DZ3v8Pdf8vdf7PeJGBmV5jZLjPbbWbXz3HOL5rZ42b2mJl9qcH4I5XEWUNV59bsZSwicibq7Rp6yMwubeSNzSwNfAa4ErgQuNbMLpxxznkEM5Fe5+4/Bny4kc+IWhJnDVUt70qzulurjEXkzNWbCF4D3Gtmz5jZI2b2QzN7ZIHXXAbsdvdn3b0A3AJcM+OcDwCfcfcXANz9aCPBR61QcbIpSCW00uc5gzn2jhfJlytxhyIibWzeMQIz2+Tue4GfWsR7rwf21TzeT5BQap0ffs7dQBr4hLv/yyxxXAdcB7Bp06ZFhLI4+XKFrlRyyzicuyzHfUen2DNWZNvyrrjDEZE2tdBV7qsA7v4j4NPu/qPaWxM+PwOcB1wOXAv8hZktn3mSu9/g7tvdffvQ0FATPrY+hQSVoJ7N+r4M3WmtMhaRM7NQIqi9Cp7d4HsfADbWPN4QPldrP7DD3Yvuvgd4iiAxJEI+QSWoZ5MKVxnvHilolbGILNpCicDnuF+PB4DzzGyrmeWAdwI7ZpzzVYLWAGa2mqCr6NkGPycySSpBPZdtK3JMl50fjRXjDkVE2tRCieBiMxs1szHgovD+qJmNmdnofC909xLwIeB24AngVnd/zMw+aWZXh6fdDjxvZo8DdwK/5e7Pn9lXap4k7U42l60DOXIp48mT+bhDEZE2Ne9gsbuf0Uold78NuG3Gcx+rue/Ab4S3xEl61xAEexmftyzHUycL/NRGJ53QGU4iklzJnRKTAO3QNQRwwfKge2ivuodEZBGUCObg7hTKyW8RAGwdDLqHdp3U7CERaZwSwRxKDhWSV3BuNtmUcc5gll0jeSqaPSQiDVIimENSS1DPZduKLqZKzt5xdQ+JSGOUCOZQLdvQnaCN6+dz9mCObAp1D4lIw9rjKheDfEL3IphLNmWcO5jjiRfylCrqHhKR+ikRzGE6TATdmfZIBACvWNXNdNlVckJEGqJEMId2axFAsIXlQDbFIyem4w5FRNqIEsEcpttsjACC2kMvX9nFntEiY4Vy3OGISJton6tci7VjiwDgolXdOPCD51VyQkTqo0Qwh+mykzZooyECAFZ0pTl7MMvDx6coa9BYROqgRDCHfLiq2Nqwds+rV/cwUXJ2adBYROqgRDCH6VKlrcYHap09mGV5LsXOo1O4VhqLyALa80rXAvk2qTM0GzPj0jU9HJwssW+iFHc4IpJwSgRzmC473W2aCCAYNO7NGN87PBl3KCKScEoEc2jnFgEEK40vHephz1iRw5NqFYjI3JQI5jBdbt8xgqpXDXXTnTa+c3Ai7lBEJMHa+0oXoXZvEUCwGO5163p5bqzInlHNIBKR2SkRzKJUcUpOW48RVL1qdTfLcinuPDihGUQiMislglm066ri2WRSxhuH+zg6VeaxF7TaWEReKtJEYGZXmNkuM9ttZtfPc97Pm5mb2fYo46lXO9YZms/LVuRY15PhroOTKlEtIi8R2ZXOzNLAZ4ArgQuBa83swlnOGwB+HbgvqlgatZRaBBCsK3jT+l5GixXuPzoVdzgikjBR/uS9DNjt7s+6ewG4BbhmlvN+F/gUkJjaye24F8FCNg/kuGB5jnsOT/JCXpVJReS0KBPBemBfzeP94XOnmNklwEZ3/9p8b2Rm15nZTjPbeezYseZHOsNSaxFUvWV9Hykz7tg3roFjETkltk5wM0sBnwY+stC57n6Du2939+1DQ0ORx7bUxgiqBnJp3jDcy7NjRZ7U3sYiEorySncA2FjzeEP4XNUA8HLgO2b2HPBaYEcSBoynS0uzRQDw6qFu1vak+db+iVMJT0Q6W5SJ4AHgPDPbamY54J3AjupBdx9x99XuvsXdtwD3Ale7+84IY6pLvk33IqhHyowrNvUzUarw3YOqQyQiESYCdy8BHwJuB54AbnX3x8zsk2Z2dVSf2wzTbbwXQT2Ge7NsH+rm4ePT7B0vxh2OiMQsE+Wbu/ttwG0znvvYHOdeHmUsjVgKdYYW8obhPp4aKfD1vWP8+20ryKaWZtITkYUt7avdIk2WnN6l2C9UI5c2rtzUzwv5CncfUheRSCdTIpjFVKlCT2bp/2m2DOS4aFUX9x2dUqlqkQ629K92izBZqiz5FkHVm8/qoy+T4ra9Y5S1tkCkIykRzODuTJWc3g5oEQB0Z1L85MagKN19R1R+QqQTdcbVrgH5slOBjugaqjp/eRfblue4+/Akz0+ri0ik03TO1a5OU2F5iU7pGqp664Z+sinjtr0qPyHSaZQIZpgsBatte5b49NGZ+rIpfmJ9HwcmSjx0PDH1/0SkBTrraleHaiLotBYBwMtXdrF1IMt3Dk4wUlCFUpFOoUQww1RYZ6iTxgiqLCw/AfAv6iIS6Ridd7VbwOkWQWf+aZbl0lx+Vh97xoo8ekJbW4p0gs682s1jquRkDLId/Je5ZHU3G/oyfOvABBNFVSgVWeo6+HI3u8lwVfFSLThXD7Og/ESx4tyxfzzucEQkYkoEMwSJoHOTQNWq7gyvX9fLkycL7DqpLiKRpUyJYIZOWlW8kMvW9rCmJ8039o0zVVIXkchSpSveDEGdIf1ZANJmXLVpgOmy888/GtMsIpElSle8GabKrq6hGut6M7x5fR/PjBa5V7WIRJYkJYIaZXfyZXUNzXTJ6m5etjzHdw9N8pTGC0SWHF3xapxaTLYEN60/E2bGVZsHOKs3w47nxtiv7S1FlhQlghrVOfO9nbyIYA7ZlPHzZw8ymEtz6zOjHJhQMhBZKiK94pnZFWa2y8x2m9n1sxz/DTN73MweMbNvmdnmKONZyFiYCAaVCGbVl01x7bmD9GaMW3aP8MxIIe6QRKQJIrvimVka+AxwJXAhcK2ZXTjjtIeB7e5+EfAV4H9HFU89RsNCawM5JYK5DOTSvPv85azsSvOVZ0d5+LgGkEXaXZRXvMuA3e7+rLsXgFuAa2pPcPc73b26c/q9wIYI41nQWLFCCujTYPG8+rMp3nXecs4ezHL7vgm+fWCCiqaWirStKK9464F9NY/3h8/N5X3A12c7YGbXmdlOM9t57NixJob4YqOFCv3ZFKkOLi9Rr1w6GDO4ZHU39x+d4tZnRk8V7BOR9pKIn75m9m5gO/AHsx139xvcfbu7bx8aGoosjrFihUF1C9UtZcZPbuznyk397BsvctOTJzk0qUFkkXYT5VXvALCx5vGG8LkXMbO3AP8DuNrdY52kPlooM6CB4oZdvKqbd5+/DICbnxrhnsOT6ioSaSNRXvUeAM4zs61mlgPeCeyoPcHMXgX8OUESOBphLAty97BFkI4zjLY13JvlvduWc/6yHHcdmuSLT49wYlq7nIm0g8gSgbuXgA8BtwNPALe6+2Nm9kkzuzo87Q+AfuDvzOz7ZrZjjreL3FTJKTtqEZyBnkyKa7YM8LOb+zk+XebGJ1/gnsOTlCpqHYgkWSbKN3f324DbZjz3sZr7b4ny8xsxGq4h0NTRM2Nm/NjKbjb1Z/nmgQnuOjTJoyfy/OSGPrYM5uIOT0RmoateaKwYdGNosLg5BnJp3r51kF88ZxDHueWZUf5pz+ipv7OIJIeueqHRQtgiyGqMoJnOHszxvm0reP26Xp4aKfAXj5/k/qNTGkwWSRAlgtBYoULKoE8lqJsukzJeP9zL+1+2go39Gb59YIK/evIkh1SvSCQRlAhCo8UKA9nO3qs4aiu60rzj7EHevjXY7Obmp0d44OiUNrwRiVmkg8Xt5MR0mRVd6haKmplxwfIuNvdn+drecb51YIK940V+elM/3SrtIRIL/csDKu4cny4x1K1E0CrdmRQ/t3Ug2P1spMBf7VJXkUhclAiAk/kKJYehHjWQWsnMuGxND+86fxnucPPTI9x3ZFJdRSItpkQAHJsuATDUoxZBHNb3BauSzxnMcefBSf72GU0zFWklJQLg2FRw0VndrRZBXHrCrqIrNvazf7zIjU+c5AfHpzXNVKQFlAgIWgQrulJkU5oxFCcz45Wru3nvtuWs6k7z9X3j/PWuk+zTHskikVIiIGgRDKk1kBirujO867xlXL15gMmS88WnR/jS0yPsOplXC0EkAh1/9StVnBfyZbatUB2cJDEzLlzZxbnLcjx8fIoHj03zj3vGGMym+LGVXVywvIu1PWmt+xBpgo5PBMemSziwRi2CRMqljdes7eXSNT08PVLg4ePT3Htkiu8dmWJZLsXZgzk2D2TZ3J+lR+sQRBal469+z44G/c8b+7MxRyLzSYUL0S5Y3sVkqcLTIwWeOpnnsRN5Hj4+DcDKrjRre9Ks682wtjfD2p6MkoNIHTo+ETwzUmC4N0Of9iFoG72ZFBev6ubiVd2U3Tk0UWLveJFDkyUOTJR44mTh1Ll9GWN1d4ZV3WlWd6dZ3ZNhdXeaXiUIkVM6OhFMFCscnCzxhuHeuEORRUqbsaE/y4aaFt1UqcKRyRJHpkocny7z/HSZR0/kKdRskNObMZbl0vRkjJ50iu6M0ZUyutJGLm10p1Msy6VY2ZVW6QtZ8jo6ETwzGvxyPFcbpiwpPZkUWwZzL9oIp7oV6fHpcngrMV6oMFlynp8uMl12CmVntjlJvRljuDfDpv4sG/uzrO3NkNYgtSwhHZ0Idp3MM5BNsUYripc8M2Mwl2Ywl+bswdnPcXeKFchXKkyXnJOFMifCxHFgosQzo5MAZFOwoS9ICpv6swz3ZkhrDYq0sY5NBPvHizwzWuT163o1BVGAIFnk0pBLpxnIhrWnlp0+PlGssG+8yN7xIvvGi9x1KEgMKYMVuTQru9Msz6Xoz6boyaToy6TozVhwP6sFi5JcHZkI3J1vHZigP5visjU9cYcjbaIvm2Lbii62regCYLIUJIZDEyVO5MucyJfZM1qgNMeat2wqGOjuzaSCsYhwTKI6LtGVCv6bTQW3XKrmfrr2OfTjRZoq0kRgZlcAfwykgc+7++/PON4FfAF4NfA88Evu/lyUMVXc+ca+CQ5NlrhqUz+5tP5ByeL0ZlKnprRWVbuXJksVJksVJkrBOMRksRI+50yWKhQqznixQqHs5CtOvtzYiulsilkTRlfa6M8GA91BV1iKZbk0fRlT8pA5RZYIzCwNfAZ4K7AfeMDMdrj74zWnvQ94wd3PNbN3Ap8CfimKePLlCk+eDBYkHZ4s8do1PbxiZdfCLxRpQG330vIGNjqqJpBCxSlWgoHrYvX+jOeCx8zynDORr/CjsSL5yosTS8pgMHs6OeRSRiZlZAzSKSNtsJg0YRa8NmNGOhXM4kpbsD1p2oLjKcCM8L+GvehxsEbEwhirr0+d+u/CrZ9q2XKv3hwqDhX81H0n+BE4233g1OcbFn5m9TmrOfbSeI2l0TqLskVwGbDb3Z8FMLNbgGuA2kRwDfCJ8P5XgD81M/MICtI/dbLA1/eOs7Irzc9s7uflK7ub/REii3Y6gTTnojJdrjBaqN7KjBYqjBTKjBYr7B0rUqg4ZXdKFWadKZUk1YThADUX7yTFbXPcr30w1//ZOZ+f5cCla3r48eG+hmKrR5SJYD2wr+bxfuA1c53j7iUzGwFWAcdrTzKz64DrwofjZrYrkojnt5oZcXWQTv3unfq9oXO/+1L+3pvnOtAWg8XufgNwQ5wxmNlOd98eZwxx6dTv3qnfGzr3u3fq945yyeQBYGPN4w3hc7OeY2YZgsl6z0cYk4iIzBBlIngAOM/MtppZDngnsGPGOTuAfxfefwfw7SjGB0REZG6RdQ2Fff4fAm4nmD56o7s/ZmafBHa6+w7gL4GbzWw3cIIgWSRVrF1TMevU796p3xs697t35Pc2/QAXEelsKqsoItLhlAhERDqcEkEdzOwKM9tlZrvN7Pq442kVM7vRzI6a2aNxx9JKZrbRzO40s8fN7DEz+/W4Y2oFM+s2s/vN7Afh9/6fccfUamaWNrOHzeyf446llZQIFlBTKuNK4ELgWjO7MN6oWuYm4Iq4g4hBCfiIu18IvBb4YIf8P88Db3b3i4FXAleY2WvjDanlfh14Iu4gWk2JYGGnSmW4ewGolspY8tz9LoLZXB3F3Q+5+0Ph/TGCC8P6eKOKngfGw4fZ8NYxs0nMbAPw08Dn446l1ZQIFjZbqYwlf1GQgJltAV4F3BdzKC0Rdo18HzgK3OHuHfG9Q38E/DegEnMcLadEIDIHM+sH/h74sLuPxh1PK7h72d1fSVAJ4DIze3nMIbWEmf0McNTdH4w7ljgoESysnlIZssSYWZYgCXzR3f8h7nhazd1PAnfSOWNErwOuNrPnCLp/32xmfxNvSK2jRLCwekplyBJiQYH5vwSecPdPxx1Pq5jZkJktD+/3EOwl8mSsQbWIu/+2u29w9y0E/8a/7e7vjjmsllEiWIC7l4BqqYwngFvd/bF4o2oNM/sy8D3gAjPbb2bvizumFnkd8CsEvwq/H96uijuoFhgG7jSzRwh+AN3h7h01jbJTqcSEiEiHU4tARKTDKRGIiHQ4JQIRkQ6nRCAi0uGUCEREOpwSgSxZZlYOp34+FlbU/IiZpcJj283sT+Z57RYz++V5jp9lZl8J77/HzP60wdjeY2Zn1Tz+fIcUtpMEimyrSpEEmArLJWBma4AvAYPAx919J7BzntduAX45fM2LmFnG3Q8S7LO9WO8BHgUOArj7+8/gvUTOiFoE0hHc/ShwHfAhC1xerTlvZm+sWTj2sJkNAL8PvCF87r+Gv+B3mNm3gW+FLYbafRo2mtl3zOxpM/t4+L4vOsfMftPMPmFm7wC2A18M378nfO328LxrzeyHZvaomX2q5vXjZvZ7YevmXjNbG/XfTTqDEoF0DHd/FkgDa2Yc+k3gg2Hr4Q3AFHA98K/u/kp3/8PwvEuAd7j7G2d5+8uAnwcuAn6helGfI46vELRG3hW+/1T1WNhd9CngzQR7AlxqZm8LD/cB94b7BdwFfKDOry4yLyUCEbgb+LSZ/RdgeVhWZDZ3uPtc+zPc4e7Phxf1fwBev8hYLgW+4+7Hwji+CPx4eKwAVEs+PEjQfSVyxpQIpGOY2dlAmaDW/inu/vvA+4Ee4G4z2zbHW0zM8/Yza7U4wU5ntf/GuhsK+KWKfromTBmN8UmTKBFIRzCzIeBzwJ/6jAJbZnaOu//Q3T9FUGxtGzAGDDTwEW81s5Vh1c63EbQyjgBrzGyVmXUBP1Nz/lzvfz/wRjNbHW6Tei3w3QbiEGmYflHIUtYT7raVJfh1fjMwW1npD5vZmwh2pnoM+Hp4v2xmPyDYu/mFBT7rfoL9CzYAfxPOSsLMPhkeO8CLSzrfBHzOzKaAf1N90t0Pmdn1BHsBGPA1d/+n+r+ySONUfVREpMOpa0hEpMMpEYiIdDglAhGRDqdEICLS4ZQIREQ6nBKBiEiHUyIQEelw/x+39TdUllO91gAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# 한달 평균 2건의 교통사고가 발생하는 지역에서 한달 교통사고 발생 간격\n",
    "l = 2\n",
    "rv = sp.stats.expon(scale=1.0/l)\n",
    "\n",
    "print(f\"f(1)={rv.pdf(1):.3f}, f(3)={rv.pdf(3):.3f}\")\n",
    "# 1달안에 교통사고가 발생할 확률, 3달안에 교통사고가 발생할 확률\n",
    "print(f\"F(1)={rv.cdf(1):.3f}, F(3)={rv.cdf(3):.3f}\")\n",
    "print(f\"E(X)={rv.mean():.3f}, V(X)={rv.var():.3f}\")\n",
    "\n",
    "# 랜덤 샘플링 후 시각화\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=30, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 카이제곱 분포 (Chi-squared($x^2$) Distribution)\n",
    "\n",
    "추정과 검정에 사용되는 특수한 확률분포 중 하나, 분산의 구간 추정이나 독립성 검정에 사용\n",
    "\n",
    "![](https://upload.wikimedia.org/wikipedia/commons/thumb/2/21/Chi-square_distributionPDF.png/270px-Chi-square_distributionPDF.png)\n",
    "\n",
    "https://ko.wikipedia.org/wiki/%EC%B9%B4%EC%9D%B4%EC%A0%9C%EA%B3%B1_%EB%B6%84%ED%8F%AC\n",
    "\n",
    "**Further Reading**\n",
    "* [카이제곱 분포](https://ko.wikipedia.org/wiki/%EC%B9%B4%EC%9D%B4%EC%A0%9C%EA%B3%B1_%EB%B6%84%ED%8F%AC)\n",
    "* [Chi-squared distribution](https://en.wikipedia.org/wiki/Chi-squared_distribution)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 18,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 18,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEGCAYAAAB/+QKOAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAm/0lEQVR4nO3deZCcd33n8fe3z7kPHdYtj6zDtgL4EjYkHCYEMJsNJlk72EAKKBInu1DZbJKqONkUppxKCjYVcmzIBgIkhECIMYF1EgfWnAESY8sXtizLlmTZOixb0txH93T3890/+plRe9wz03M8fX5eVV3z9HP0/KbVer79u74/c3dERETmitW6ACIiUp8UIEREpCwFCBERKUsBQkREylKAEBGRshK1LsBqWbdunQ8MDNS6GCIiDeWBBx446+7ryx1rmgAxMDDA/v37a10MEZGGYmbPzHdMTUwiIlKWAoSIiJSlACEiImUpQIiISFkKECIiUpYChIiIlKUAISIiZSlA1IjSrItIvWuaiXKNZDBT4ItHRigEzkB3irdu7yIRs1oXS0TkRVSDqLJMPuDOo6PkwuBwYCjL146Pq0YhInVHNYgq+97pSYanC9y8q5dtXUn603G+f3qSLZ0JrljXXuviiYjMUg2iigJ3Dg5l2dObYltXEoCf2NjOtq4E339uklygWoSI1A8FiCp6djzHZN65pD89u8/MeN2mTibyzkNnMzUsnYjIiylAVNHBoSzJGOzsSb1o/7auJAPdSe59XrUIEakfChBVErjz5PA0u3vTJMuMWHrVhnYm886h4WwNSici8lIKEFVyZqrAVMHZ2ZMse/zCriT96RgPq5lJROqEAkSVnJ7KA7Cpo3yAMDMuW9vGiYk85zL5ahZNRKQsBYgqeX4yTypm9Kfnf8tfvqaNGPDIOTUziUjtKUBUyenJPBs64pjNP2O6Mxnjop4UB4eymjgnIjWnAFEFgTsvTOXZ2L74vMRL+1OM5QJOTKiZSURqSwGiCs5lCuQdNnQsHiB296ZJWHFIrIhILSlAVMHpyWJtYGMFASIVN3b1pnhiOEugZiYRqSEFiCp4fipPMgZr0vGKzr+kL81k3jk+nou4ZCIi81OAqILBbIE16TixBTqoS13UkyJucHhkOuKSiYjMTwGiCoazAX0V1h6g2Mx0YXeSp0amNZpJRGpGASJigTsj0wX6UpUHCIDdvSmGpwPOZgoRlUxEZGEKEBEbzwUUHPoWmCBXzq7eYkK/p9TMJCI1ogARsaFssQbQv8QaRHcyzqaOhPohRKRmFCAiNjwdACypD2LGrt4UpybzjOeC1S6WiMiiFCAiNpItYEB3aulv9e6wmUm1CBGpBQWIiA1lC/SkYsQrHOJaan1bnN5UjKdGNKtaRKpPASJiw9MB/ctoXoJiCvDdvSmeGcsxXdBwVxGpLgWIiA0vY4hrqV29KfIOx8bUzCQi1aUAEaFsIWAq70se4lpqW1eSdNw03FVEqk4BIkIj4Qim3hXUIOJm7OxJcWR0Wsn7RKSqFCAiNBEOT+1Kruxt3t2bYjLvnNIaESJSRZEGCDO7zswOmdlhM7u1zPFfN7PHzexHZvZNM7uw5Nh7zOyp8PGeKMsZlbFVChA7epLETLOqRaS6IgsQZhYHPg68FdgL3Gxme+ec9hCwz91fAdwJ/K/w2jXAbcA1wNXAbWbWH1VZozK+SgGiLR5je1dSAUJEqirKGsTVwGF3P+ru08AXgetLT3D3b7v7ZPj0XmBruP0W4B53H3T3IeAe4LoIyxqJ8VxAOm4kY0ufAzHX7t4Ug9kC5zJqZhKR6ogyQGwBjpc8PxHum8/7gX9dyrVmdouZ7Tez/WfOnFlhcVffeC5Yce1hxi7NqhaRKquLTmozezewD/jDpVzn7p90933uvm/9+vXRFG4FxnMBXYnVeYt7U3EuaI+rmUlEqibKAHES2FbyfGu470XM7KeA/wm8zd2zS7m23q1mDQKKzUwnJ/JM5pW8T0SiF2WAuB/YbWY7zCwF3ATcVXqCmV0BfIJicHih5NDXgTebWX/YOf3mcF/DcHfG86sdINI48OSwahEiEr3IAoS754EPUryxHwTucPcDZna7mb0tPO0PgS7gS2b2sJndFV47CPwexSBzP3B7uK9hTBWcwFc+gqnUhvY4/ekYB4eUvE9EopeI8sXd/W7g7jn7PlSy/VMLXPsZ4DPRlS5aM0Ncu1cxQJgZe/vT/OD01Ko3X4mIzKU7TERmAkTnKt/EL+1PA/CEahEiEjEFiIhEUYMAWNeW4IL2OI8rQIhIxBQgIhJVDQJgb3+aU5N5hsP1rkVEoqAAEZHxXEDbKs2inuuSvmIzkzqrRSRKChARGc8FkdQeAPrScbZ0JtTMJCKRUoCIyGQ+oCOx+rWHGZf2pzmTKXB2SrmZRCQaChARmco7HauUZqOcS/rSGHBAtQgRiYgCRESKNYjo3t6uZIwdPUkODGZxrTQnIhFQgIhA4M5UwWmPsIkJ4GX9bYzmAp4dz0X6e0SkNSlARCCTL36jj7IGAbC7L0UqZjw2qGYmEVl9ChARmMm2GnWASMaMi/tSHBqeJheomUlEVpcCRAQmZ2sQ0TYxAbxsTZrpwLVOhIisOgWICMzUINrj0b+927uS9CRjHBjMRP67RKS1KEBEYKoQNjElo69BmBl716Q5OppjIqeFhERk9ShARGC2iakKNQiAl/UXFxI6OKzOahFZPQoQEZjMB6TjRjyCPEzlrGtPsL4trhTgIrKqFCAiMJkLaI9XJzjMuLgvzYmJ/GwWWRGRlVKAiMBUIdo0G+Vc0pcC4JCamURklShARCDqNBvlrGtPsLYtzhMKECKyShQgIjCZ96rMgZjr4t4UJ8bzTOXVzCQiK6cAscrcncl8QHuVaxAAu3pTOHB0VJPmRGTlFCBW2XTgBF6dWdRzbepI0JkwDmtWtYisAgWIVTZZpUR95ZgZO3tSHB3LUVAKcBFZIQWIVTbT/l+LJiaAnb0psgXnhFKAi8gKKUCsskyh+M096rUg5rOjO0XM4OioAoSIrIwCxCqbWQuircoT5Wak4saWzgTHxtQPISIrowCxymYS9bVVKQ9TOQPdKZ6fKjCpWdUisgIKEKtspompVjUIgB3dSQCeUT+EiKyAAsQqy+QDkjGqlqivnI0dCdJx42k1M4nICihArLJMwWvavAQQM+PCriTHRnO4hruKyDIpQKyyYoCoXe1hxo6eJKO5gKGs+iFEZHkUIFZZphDQVqMhrqUGuovZXdXMJCLLpQCxyjL52jcxAfSlYvSmYhwbU0e1iCxP7e9kTaZempjMjIHuJM+O5QjUDyEiy6AAscoyhaAuAgQUZ1VnA+fURL7WRRGRBhRpgDCz68zskJkdNrNbyxx/nZk9aGZ5M7thzrGCmT0cPu6KspyrpRA4uQDaapSHaa4Lw/kQamYSkeWI7E5mZnHg48Bbgb3AzWa2d85pzwLvBb5Q5iWm3P3y8PG2qMq5mmbzMNVJDaI9EWNju9JuiMjyRPlV92rgsLsfdfdp4IvA9aUnuPsxd/8R0BRjMeshzcZcA91JTk3kmS6oH0JElibKO9kW4HjJ8xPhvkq1mdl+M7vXzN5e7gQzuyU8Z/+ZM2dWUNTVMZuorw6Guc4Y6E4SAMeVdkNElqiiAGFmL4+6IGVc6O77gHcCf2JmO+ee4O6fdPd97r5v/fr11S/hHPWQh2muLV1J4oaamURkySqtQfyFmd1nZv/NzHorvOYksK3k+dZwX0Xc/WT48yjwHeCKSq+tlUwdNjElY8bWzqQ6qkVkySq6k7n7a4F3UbzhP2BmXzCzNy1y2f3AbjPbYWYp4CagotFIZtZvZulwex3wE8DjlVxbS/XYxATFZqYzmQITSv8tIktQ8Vddd38K+F3gt4DXA39mZk+Y2c/Nc34e+CDwdeAgcIe7HzCz283sbQBm9kozOwHcCHzCzA6El18K7DezR4BvAx9x9/oPEHXYxATFAAHwjGoRIrIEiUpOMrNXAO8Dfhq4B/gZd3/QzDYD/wH8Y7nr3P1u4O45+z5Usn0/xaanudf9O1CLfo8VyRQCUjEjZvUVIDaE6b+PjU+zd0261sURkQZRUYAA/jfwKeB33H1qZqe7nzKz342kZA0oU/C6a16Cl6b/tjoLYCJSnyoNED9NceJaAcDMYkCbu0+6++ciK12DmcrXT5qNuQa6kzw5Ms3wdEB/Ol7r4ohIA6i0D+IbQHvJ845wn5TI1sFiQfOZTf89quGuIlKZSu9mbe4+PvMk3O6IpkiNq14yuZbTn47Rk4rxtDqqRaRClQaICTO7cuaJmV0FTC1wfkvK5J32OuyDgGL67509KZ4Zy5EPlHZDRBZXaR/ErwFfMrNTgAEbgXdEVahGNVUI6raJCWBnT4qHzmY4MZ5joCdV6+KISJ2rKEC4+/1mdglwcbjrkLurraJELnAKXn9zIEptD9NuHBmdVoAQkUVVWoMAeCUwEF5zpZnh7n8bSaka0GyajTptYgJIxY3tXUmOjOZ4Y60LIyJ1r9KJcp8DdgIPA4VwtwMKEKHZNBt13MQExWamb5ycYChb0HBXEVlQpTWIfcBedy1uPJ96TbMx187eYoA4OjrNVevbF79ARFpWpV93H6PYMS3zaIQmJoD+dJz+dIwjmg8hIouotAaxDnjczO4DsjM7G2Up0GqYaWJqr/MmJig2Mz18NkMucJKx+g5oIlI7lQaID0dZiGbQKE1MUAwQ+89keHYsx85ejWYSkfIqXQ/iu8AxIBlu3w88GGG5Gs7MetTpBggQ27qSJGNwWM1MIrKASpcc/SXgTuAT4a4twFcjKlNDyuSddNwaIlNqImZc1JPiqZFpNO5AROZTaYP5Byiu6jYKs4sHXRBVoRpRtuC0N0DtYcae3hTjuYBTk/laF0VE6lSlASLr7rPtEWaWoDgPQkKZOk+zMdfOnhQxgyeH1cwkIuVVekf7rpn9DtAerkX9JeCfoitW45nK1+diQfNpS8QY6EpyaDirZiYRKavSAHErcAZ4FPhlisuIaiW5EvWc6ns+e/rSDE8HnMkUFj9ZRFpOpcn6AuCvwoeUUWxiSta6GEuyuzfF144Xm5kuaF9KWi4RaQWV5mJ6mjJ9Du5+0aqXqAG5e92uR72QzmSMrZ0JDg1nec0mrf8kIi+2lFxMM9qAG4E1q1+cxpQLIKjzVN/zubgvzTeVvE9Eyqh0oty5ksdJd/8T4KejLVrjmM3D1ECjmGbs6SvOpH5yOLvImSLSaiptYrqy5GmMYo1Cjdah2TQbDdbEBNCbirOxPcETw9Ncs0HNTCJyXqU3+T8q2c5TTLvx86temgZ1fi2IxgsQAJf2p/j2qUmGswX61MwkIqFKRzG9IeqCNLKpBm5iArikP823T01ycCjLqzeqFiEiRZU2Mf36Qsfd/WOrU5zG1EiZXMvpTcXZ0pngcQUIESlR6VfefcB/pZikbwvwK8CVQHf4aGmZfLEG0d6AfRAzLu1PcyZT4OyUcjOJSFGlfRBbgSvdfQzAzD4M/Iu7vzuqgjWSbMExINXAi+9c0pfmmycmODic5bWaNCciVF6D2ACUZnWbDvcJMBWm2WiEVN/z6UrG2N6V5OCQUoCLSFGlXxX/FrjPzL4SPn878NlIStSAMvmgIYe4znVpf5qvHR/n+akCGztUixBpdZVOlPt94H3AUPh4n7v/QZQFayTFRH2NOYKp1J6+FDHg4JAmzYlI5U1MAB3AqLv/KXDCzHZEVKaG04iZXMvpSMTY0ZPk8aEsgZqZRFpepUuO3gb8FvDb4a4k8HdRFarRFDO5Nn6AAHjZmjbGcgHPjOVqXRQRqbFKaxA/C7wNmABw91NoeOusTN5pSzR+ExMUU4Cn48ajg2pmEml1ld7Vpr04tMUBzKyzkovM7DozO2Rmh83s1jLHX2dmD5pZ3sxumHPsPWb2VPh4T4XlrLqZVN+NtB71QhIxY29/mieHs2TDGeIi0poqDRB3mNkngD4z+yXgGyyyeJCZxYGPA28F9gI3m9neOac9C7wX+MKca9cAtwHXAFcDt5lZf4Vlraps4DiQbpIAAfDyNWnyDk9ovWqRlrboWEYrDu7/B+ASYBS4GPiQu9+zyKVXA4fd/Wj4Ol8ErgcenznB3Y+Fx+Z+VX0LcI+7D4bH7wGuA/5+8T+pumYT9TVJExPApo4Ea9JxHj2X4bK1bbUujojUyKIBwt3dzO5295cDiwWFUluA4yXPT1CsESz32i1zTzKzW4BbALZv376Eoq2eRs/DVI6Z8fI1ab773KQWEhJpYZV+7X3QzF4ZaUmWwd0/6e773H3f+vXra1KGmcWC2ptgHkSpl61JY8Cjg5laF0VEaqTSu9o1wL1mdsTMfmRmj5rZjxa55iSwreT51nBfJVZybVWdb2JqnhoEQHcqzkB3kkfPaU6ESKtasInJzLa7+7MU+wSW6n5gdzih7iRwE/DOCq/9OvAHJR3Tb+b8HIy60oxNTDMuX9fGV54e48joNLt707UujohU2WI1iK8CuPszwMfc/ZnSx0IXunse+CDFm/1B4A53P2Bmt5vZ2wDM7JVmdgK4EfiEmR0Irx0Efo9ikLkfuH2mw7reNPJ61IvZ1ZuiKxnj4bNqZhJpRYt1Upd+Lb5oqS/u7ncDd8/Z96GS7fspNh+Vu/YzwGeW+jurLVNwYgbJ5osPxM24bG2aH5ye0nKkIi1osduaz7MtoUy+8VN9L+SytW0Y8Mg51SJEWs1iAeIyMxs1szHgFeH2qJmNmdloNQpY74p5mJqw+hDqScXZ1ZvikXMZCoG+I4i0kgXvbO4ed/ced+9290S4PfO8p1qFrGeZgjf0UqOVuGJdG5N558kRzawWaSXN+9W3SmaamJrZju4kvakYD56dqnVRRKSKFCBWaKrJm5igOLP6inVtHB/P88JUvtbFEZEqae47WxVk8s3fxATFzuqEwYNn1Fkt0ioUIFag4E42aI7lRhfTnojxY2vSHBjKkMkrDbhIK2j+O1uEZtJstEINAuCq9e3kAg15FWkVChAr0KyJ+uZzQXuCbV0JHjybUX4mkRbQGne2iEw1aaK+hVy1rp2R6YAjoxryKtLsFCBWYGqmBtFCAWJPX4ruZIwH1Fkt0vQUIFZgtg+iRZqYAGLhkNdjYznOZjTkVaSZtc6dLQJTTZzqeyGXr20jriGvIk1PAWIFMvkAA9ItFiA6kjEu7U/z6GBmtqNeRJqPAsQKTBWctkTzZnJdyL5wyOuj57K1LoqIREQBYgUy+aCl+h9KbexIsKUzwYNnp3ANeRVpSq15d1slUy2QyXUhV61vZygbcHQ0V+uiiEgEFCBWYCoftFwHdamL+1J0JWI8cEZZXkWakQLEChTXgmjdtzBuxuXr2jg6lmMwU6h1cURklbXu3W0VTLXAWhCLuXxdGzGDB7RWhEjTUYBYpoI700Fr1yAAupIxLu1L8+i5LFkNeRVpKq19d1uB87OoW7sGAXDV+jamA9eQV5EmowCxTDN5mNpavAYBsLkzydbOBPe9MEUh0JBXkWahu9syqQbxYq/e0MFoLuCxIdUiRJqFAsQyna9BKEAAXNSTZEN7nHufn9RaESJNQgFimSbDGkSHmpgAMDNevbGDoWzAoWGtFSHSDHR3W6bJXLEGoQBx3sW9Kdam4/z76Uml3xBpArq7LdNkPiAZg2RMTUwzzIxXbWjnTKbAYa04J9LwFCCWaTLvqj2UsXdNmr5UjO89p1qESKPTHW6ZJvOBAkQZcTNet6mTF6YKPK4RTSINTXe4ZSoGCDUvlXNpf4oN7XH+7blJzYsQaWAKEMukJqb5mRmv39zJyHTAQ+e0LKlIo9Idbhncncl8QKcCxLx2dCe5sCvJv5+eVI4mkQalO9wyZAOn4LT0YkGLMTOu3dzBZN754QvK9CrSiBQglmEyV2xX70zq7VvIps4ke/vT3Pf8FMNZrRch0mgivcOZ2XVmdsjMDpvZrWWOp83sH8LjPzSzgXD/gJlNmdnD4eMvoyznUk3mNUmuUtdu7sAMvnVyotZFEZEliuwOZ2Zx4OPAW4G9wM1mtnfOae8Hhtx9F/DHwEdLjh1x98vDx69EVc7lUICoXE8qzo9v6ODJkWme1uQ5kYYS5R3uauCwux9192ngi8D1c865HvhsuH0n8EYzq/uG/fN5mOq+qHXhlRe005+Occ+JCQ17FWkgUQaILcDxkucnwn1lz3H3PDACrA2P7TCzh8zsu2b22gjLuWSqQSxNIma8cUsXg9kC+8+ow1qkUdTrHe45YLu7XwH8OvAFM+uZe5KZ3WJm+81s/5kzZ6pWuIl8QCpmJJSHqWK7elPs6k3xvecmGcyow1qkEUQZIE4C20qebw33lT3HzBJAL3DO3bPufg7A3R8AjgB75v4Cd/+ku+9z933r16+P4E8obyrval5ahrds6yQeM+5+dkxrRog0gCgDxP3AbjPbYWYp4Cbgrjnn3AW8J9y+AfiWu7uZrQ87uTGzi4DdwNEIy7okEznlYVqO7mScn9rSyYmJPPc+r6YmkXqXiOqF3T1vZh8Evg7Egc+4+wEzux3Y7+53AZ8GPmdmh4FBikEE4HXA7WaWAwLgV9x9MKqyLtVkPqA3Fa91MRrSy9akeXosx/eem2RLZ4ILu1O1LpKIzCOyAAHg7ncDd8/Z96GS7QxwY5nrvgx8OcqyrcR4PmBLZ7LWxWhIZsZbtnVyejLPV4+N8Qu7+1jTpmArUo/UTrJE+cCZyjvdKb11y5WOx7hxZ3HMwR1HRhjLqdNapB7pLrdE4+FSo91Ks7Ei/ek4N1zUw0Q+4PNPjigVh0gd0l1uicYUIFbNls4kN+/qJVNw/u7JEc5M5WtdJBEpobvcEo1NK0Csps2dSd61uxeAzz81wsmJXI1LJCIzdJdbopn28i71Qaya9e0J3r2nl7a48fdPjXBkRDmbROqB7nJLNJYrzqJOaxb1qupLx/mFPX2sbYvz5aOjPDaolehEak0BYonGcgFdyRgNkFOw4XQmY7xzdy/bupL88zPjPHxWQUKklhQglmhsOlD/Q4RmhsDu7EnytePjHBzK1rpIIi1Ld7olGs8FmgMRsUTMePuOHrZ2JvinZ8Y4qnUkRGpCd7olCNwZy6kGUQ3JmHHDRT2sa4vzladHNbpJpAZ0p1uCybzjaIhrtbQlYrxjZy+diRh3HhnlXEbzJESqSXe6JRibLg5xVRNT9XQmY7xjVy9mcMeR0dmZ7CISPd3pluD8LGoll6um/nScG3f2MJkPuOPICNmCgoRINShALMFIOIu6RzWIqtvUkeTtAz2cmSrwpSOjTBe04JBI1HSnW4LBbIG2uNEe1xyIWtjZm+JtA92cnMhzx5ERMnnVJESipACxBIOZAmvScU2Sq6FL+9NcP9DNqck8n3tKWWBFoqQAsQSD2QL9afU/1Nol/Wlu2tnLeC7grw8N84Qm04lEQgGiQtOF4hwIrX5WH7Z3J3nfxX2sScf56rExvnx0VLUJkVWmAFGhofDms0Y1iLrRl47z7t29XLu5g2Nj03zq4BA/OD1JLlAHtshqiHRN6maiAFGf4jHjVRs62Nuf5psnJ/jec5M8fDbDazZ28PK1aWLqLxJZNtUgKjQYBgj1QdSnnlScn93Rwzt399KdjPGvx8f59MFhDg1ncVeNQmQ5FCAqNJgt0J2MkdIQ17q2vSvJL+zp5ed2dAPwlafH+NyTIzw7plxOIkulJqYKzQxxlfpnZuzpS7OrN8Wjg1m+/9wkXzg8wkU9SV6/qZMNHfrYi1RCNYgKuDvnMgWNYGowMTMuW9vGLXv7ecPmDk5O5PnrQ8P807ExjXgSqYC+SlXgbKZANnA265tnQ0rGjGs2dHDZ2jbufX6K/WemODic5fK1bVy1vo21bfp3FSlH/zMqcGqimGZ6S2eyxiWRlWhLxLh2SydXrW/j+6cneeRchgfPZhjoTnLFujYu6kmR1FrjIrMUICpwYiJHe9zoT6tFrhl0p+K8dXs3r9vUySPnMjx0NsNXnh4jGYMd3Sl29abY1pWkL6W1x6W1KUBU4NREns2dCd0smkxnMsaPb+zgmg3tHB/L8eTI9OwDoCNhbO5MsqkjMftoT+hLgrQOBYhFTOUDzmULvGxNutZFkYjEzRjoSTHQk+JNW52zmQInJ/KcmMhxaiLP4ZHza2L3pWJc2J1kT2+aC7uTJNQkJU1MAWIRM/0Pmzv1VrUCM2N9e4L17QkuX9cGQCYfcHoqz3MTeU5N5jk4NM0j57KkYsaevhRXrGtjc4dqmNJ8dNdbxJHRaRJWXLBGWlNbIsZAd4qB7hQA+cB5ZizHoeEsTwxP89hglvVtcS5f18aPrUnTFlczlDQHBYgF5APn8aEse/rSmkEtsxIxY2dvip29Kd64NeDg0DQPnZ3inhMTfOfUBJf2p7libRsbVauQBqcAsYAjo9NkCq7+B5lXOh7j8nVtXLY2zenJPA+dy3BwKMuPzmXZ0B7nop4UGzsS9KXi9KVjpFW7kAaiALGARwezdCViDHSreUkWZmZs6kyyqTPJT27p5PHBLI8NZvnh81OULozaFje6kjE6EzG6ksVHTyo2G0B6U3F1fEvdUICYx6mJHEdGprnmgnaljJYlaYvHuHJ9O1eub2e64AxmCwxnCwxPFxidDhjPBUzkA05M5BjPBRTmJJvtSsRmg0VvOgwe4XZ3MqbPo1SNAkQZ+cC5+9lxupIxXrWxvdbFkQaWihsbOxJsnCdNi7szkXeGswVGpgsMTwfhdsDx8RyPDwWUxo+YQWciRlvcSMeNtnis+DNh4b7zx9IxIxU3UnN+KsBIpSINEGZ2HfCnQBz4lLt/ZM7xNPC3wFXAOeAd7n4sPPbbwPuBAvCr7v71KMs6I1MI+JdnxjmbKXDjRT0akSKRMjO6ksVmp628tCmzEDijufNBYzhbYCIfkCk42YIzmiuQzfjs80okY7woaHSEzV3dYZNXd+p881dnQjWWVhZZgDCzOPBx4E3ACeB+M7vL3R8vOe39wJC77zKzm4CPAu8ws73ATcCPAZuBb5jZHnePJAXnZD7gXKbAs+M5HjmbYSwX8MYtnezsTUXx60QqFo8Z/el4RQtVuReDxEywmA6c6ZKf2bnPCwHTgTOZd85kckzkXlxbATCKM87b40bcjHisOLEwbmBWPF48z178PNw2mB3JVf7Yi68HCNwJHBxwLz6H4uixRMxIWJntOWWb+RmLnX8eM2a3S8u6FDZnw0pexeY5b+7vsTlPXnrcXvIenX/vqhuso6xBXA0cdvejAGb2ReB6oDRAXA98ONy+E/hzK74D1wNfdPcs8LSZHQ5f7z9Wu5Cj0wX+4sDQ7PNtXQl+ZqCbbV3qmJbGYhY2NS3zf3XgzkS+2EcyFvaVjOcCxnIB2YJTcKfgxSbYfHD+Bu74bGDx8MZeuu04M4v6efjAz2/PrPg3c11s5gZpxfUIYmY4TiGAvBd/dz7wF3X+t5K5gcPCeVrv3N276r8rygCxBThe8vwEcM1857h73sxGgLXh/nvnXLtl7i8ws1uAW8Kn42Z2aHWKvmTrgLM1+t31oNX/ftB7oL+/xn//u5Z/6YXzHWjoTmp3/yTwyVqXw8z2u/u+WpejVlr97we9B/r7m/Pvj7IH9iSwreT51nBf2XPMLAH0UuysruRaERGJUJQB4n5gt5ntMLMUxU7nu+accxfwnnD7BuBbXmyQvAu4yczSZrYD2A3cF2FZRURkjsiamMI+hQ8CX6c4zPUz7n7AzG4H9rv7XcCngc+FndCDFIMI4Xl3UOzQzgMfiGoE0yqpeTNXjbX63w96D/T3NyGbGUEgIiJSSrPARESkLAUIEREpSwFiBczsOjM7ZGaHzezWWpenFszsmJk9amYPm9n+Wpcnamb2GTN7wcweK9m3xszuMbOnwp/9tSxj1OZ5Dz5sZifDz8HDZvafalnGKJnZNjP7tpk9bmYHzOy/h/ub7nOgALFMJalE3grsBW4OU4S0oje4++XNOA68jL8Brpuz71bgm+6+G/hm+LyZ/Q0vfQ8A/jj8HFzu7ndXuUzVlAd+w933Aq8CPhD+32+6z4ECxPLNphJx92lgJpWINDF3/zeKI+5KXQ98Ntz+LPD2apap2uZ5D1qGuz/n7g+G22PAQYqZHpruc6AAsXzlUom8JB1IC3Dg/5nZA2Hqk1a0wd2fC7dPAxtqWZga+qCZ/Shsgmr45pVKmNkAcAXwQ5rwc6AAISv1Gne/kmJT2wfM7HW1LlAthRM9W3Hs+P8BdgKXA88Bf1TT0lSBmXUBXwZ+zd1HS481y+dAAWL5lA4EcPeT4c8XgK9QbHprNc+b2SaA8OcLNS5P1bn78+5ecPcA+Cua/HNgZkmKweHz7v6P4e6m+xwoQCxfJalEmpqZdZpZ98w28GbgsYWvakqlKWPeA/zfGpalJmZujKGfpYk/B+GSBJ8GDrr7x0oONd3nQDOpVyAcyvcnnE8l8vu1LVF1mdlFFGsNUEzb8oVmfw/M7O+Baymmd34euA34KnAHsB14Bvh5d2/aTtx53oNrKTYvOXAM+OWS9vimYmavAb4HPAqzy1L8DsV+iKb6HChAiIhIWWpiEhGRshQgRESkLAUIEREpSwFCRETKUoAQEZGyFCCkJZlZIcw6esDMHjGz3zCzWHhsn5n92QLXDpjZOxc4vtnM7gy332tmf77Esr3XzDaXPP9UCyeClBqKbMlRkTo35e6XA5jZBcAXgB7gNnffDyyUunwAeGd4zYuYWcLdT1FcY3253ktxotkpAHf/xRW8lsiyqQYhLS9ME3ILxWRzZmbXmtk/A5jZ60vWOHgonDn+EeC14b7/EX7jv8vMvgV8M6xhlM4k3mZm3wnXCbgtfN0XnWNmvxmuqXADsA/4fPj67eG1+8Lzbg7X33jMzD5acv24mf1+WBu618waPlGc1J4ChAjg7kcpzoi/YM6h3wQ+ENY2XgtMUczz/71w3YM/Ds+7ErjB3V9f5uWvBv4L8Argxpmb/TzluJNi7eVd4etPzRwLm50+CvwkxVnLrzSzt4eHO4F73f0y4N+AX6rwTxeZlwKEyMJ+AHzMzH4V6HP3/Dzn3bNAWoV73P1ceLP/R+A1yyzLK4HvuPuZsByfB2ay504D/xxuP0CxGUxkRRQgRJjNK1VgTgZOd/8I8ItAO/ADM7tknpeYWODl5+azcYqrkpX+/2tbUoFfKufn8+YUUP+irAIFCGl5ZrYe+Evgz31OcjIz2+nuj7r7Rylm8L0EGAO6l/Ar3hSuV9xOcZWxH1BMcneBma01szTwn0vOn+/17wNeb2brwiVvbwa+u4RyiCyJvmVIq2o3s4eBJMVv858DPlbmvF8zszdQzNp5APjXcLtgZo9QXJ95aJHfdR/FtQO2An8XjpLCzG4Pj50Enig5/2+AvzSzKeDVMzvd/TkzuxX4NmDAv7h7w6eUlvqlbK4iIlKWmphERKQsBQgRESlLAUJERMpSgBARkbIUIEREpCwFCBERKUsBQkREyvr/ri6HSkbf754AAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Chi-squared distribution degree of freedom = 3\n",
    "rv = sp.stats.chi2(df=3)\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### T 분포 (T Distribution)\n",
    "\n",
    "추정과 검정에 사용되는 특수한 확률분포 중 하나, 모분산을 알 수 없고, 표본 크기가 작을 때 정규분포 Z값 대신 T 분포의 T값을 이용해 추정 또는 검정에 사용 \n",
    "\n",
    "$$t = \\frac{\\bar{x} - \\mu}{\\frac{s}{\\sqrt{n}}}$$\n",
    "\n",
    "![](https://upload.wikimedia.org/wikipedia/commons/thumb/4/41/Student_t_pdf.svg/325px-Student_t_pdf.svg.png)\n",
    "\n",
    "https://en.wikipedia.org/wiki/Student%27s_t-distribution\n",
    "\n",
    "**Further Reading**\n",
    "* [Student's t-distribution](https://en.wikipedia.org/wiki/Student%27s_t-distribution)\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 19,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 19,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEGCAYAAAB/+QKOAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkyUlEQVR4nO3de5Bc5X3m8e/T3XOTkLhJ2LHERYBiBxsCZMDZSmxyARuv14gkEIPjCs46YclCJVkntcbBBS5SrvKlQm4msVmHWtsxIcTORZvIRbCNnStGwmBjgQlC2EYCmwGBJDQz3dPdv/3jnB61hp6Z7lGfPj2t51M1RZ9rvwdN9zPv+57zvooIzMzM5irkXQAzM+tPDggzM2vJAWFmZi05IMzMrCUHhJmZtVTKuwDdsmbNmjjllFPyLoaZ2bLywAMPPBcRa1ttG5iAOOWUU9i2bVvexTAzW1YkfXe+bW5iMjOzlhwQZmbWkgPCzMxackCYmVlLDggzM2vJAWFmZi05IMzMrCUHhFkf8LD71o8yDQhJF0t6TNIOSde32H6NpIclPSTpXyWdka4/RdJUuv4hSR/PspxmefrWnmn+bPsL7K3U8i6K2SEyCwhJReBW4C3AGcCVjQBockdEnBkRZwMfAW5p2vZERJyd/lyTVTnN8vb9ySr7Zur8/ZP7qdVdk7D+kWUN4nxgR0TsjIgKcCewqXmHiNjXtLgS8KfDjjiT1aAoeHqyygPPTeddHLNZWQbEOuCppuVd6bpDSLpW0hMkNYjfaNq0QdKDkr4q6Q0ZltMsV5PVOq8YK7GiJPZMu5nJ+kfundQRcWtEnAa8F3h/uvoZ4KSIOAd4D3CHpNVzj5V0taRtkrZNTEz0rtBmXTRZrbNiqMBoscB0rZ53ccxmZRkQu4ETm5bXp+vmcydwKUBElCPi+fT1A8ATwA/PPSAibouI8YgYX7u25Wi1Zn1vciZYURKjRTFdcyur9Y8sA2IrsFHSBknDwBXA5uYdJG1sWnwr8Hi6fm3ayY2kU4GNwM4My2qWi4hgslpnZanAaElMVx0Q1j8ymw8iIqqSrgPuBorA7RGxXdLNwLaI2AxcJ+lCYAZ4AbgqPfyNwM2SZoA6cE1E7MmqrGZ5KdeCOrCiVGCsWGDP9EzeRTKblemEQRGxBdgyZ92NTa9/c57jPg98PsuymfWDA9Wkz2FFSYy4icn6TO6d1GZHssm0SWlFo4mpFn6q2vqGA8IsR5OzNYjkLiZImp3M+oEDwixHswExJMaKAnAzk/UNB4RZjg7MpE1MxaSJCRwQ1j8cEGY5mqzWGS2KYkGzTUxTVT8sZ/3BAWGWo8lqnRWl5GM46iYm6zMOCLMcTVaTp6iBpiYm1yCsPzggzHJ0aA0i+a+fprZ+4YAwy1FzQAwVRFFuYrL+4YAwy0k94pAmJiAdsM9NTNYfHBBmOamkNYWx0sGP4Wip4BqE9Q0HhFlOGkEwUjxYgxgriin3QVifcECY5aQREKNNATHiJibrIw4Is5yU0yBorkEks8q5BmH9wQFhlpPybBNTcx+EJw2y/uGAMMtJqyamsWKBSj2oe8hv6wMOCLOclOfpg2jeZpYnB4RZThqd0cNNATHsgLA+4oAwy0m5FowUREFNNYhC8rpSd0BY/hwQZjmZrsUhdzDBwRrEjAPC+oADwiwn5RYBMdSoQbiJyfpApgEh6WJJj0naIen6FtuvkfSwpIck/aukM5q2vS897jFJb86ynGZ5mK7VZ4f4bhh2E5P1kcwCQlIRuBV4C3AGcGVzAKTuiIgzI+Js4CPALemxZwBXAK8FLgb+ND2f2cBI+iAO/Qg2mphcg7B+kGUN4nxgR0TsjIgKcCewqXmHiNjXtLgSaHwqNgF3RkQ5Ip4EdqTnMxsYrZqYXIOwflLK8NzrgKealncBr5+7k6RrgfcAw8DPNB1735xj17U49mrgaoCTTjqpK4U265XpWry8ick1COsjuXdSR8StEXEa8F7g/R0ee1tEjEfE+Nq1a7MpoFkGIqJlDaIkEK5BWH/IMiB2Ayc2La9P183nTuDSJR5rtqyU642nqA/9CEpiuCgHhPWFLANiK7BR0gZJwySdzpubd5C0sWnxrcDj6evNwBWSRiRtADYC92dYVrOeKreYC6JhuCA3MVlfyKwPIiKqkq4D7gaKwO0RsV3SzcC2iNgMXCfpQmAGeAG4Kj12u6S7gEeAKnBtRNSyKqtZrzVGbB2dLyBcg7A+kGUnNRGxBdgyZ92NTa9/c4FjPwh8MLvSmeVnwRpEUcy4BmF9IPdOarMjUWOgvrl9EJA8Te0ahPUDB4RZDharQTggrB84IMxy0GqyoAZ3Ulu/cECY5WDRu5hcg7A+4IAwy0G5VmeowCFzQTQMF12DsP7ggDDLQbn+8oH6GoYLohp4XmrLnQPCLAeVWhwy1Wiz2fGY3MxkOXNAmOWgUo/ZkVvnGvakQdYnHBBmOViwBuEhv61POCDMclCpL97E5KepLW8OCLMcVGrByDxNTEPpp7LsGoTlzAFhloPyAjWIkXT4jRkHhOXMAWGWg0pt/k7qRg3CndSWNweEWY/VIqgFvs3V+p4DwqzHGjUD3+Zq/c4BYdZjjZqBb3O1fueAMOux2YH65qlBSGKo4BqE5c8BYdZjs01M89QgwCO6Wn9wQJj12GwT0zw1CPCIrtYfHBBmPeYahC0XmQaEpIslPSZph6TrW2x/j6RHJH1T0pckndy0rSbpofRnc5blNOuldmoQnpfa+kEpqxNLKgK3AhcBu4CtkjZHxCNNuz0IjEfEpKRfBz4CvD3dNhURZ2dVPrO8VBaYTa5hpCgOzDggLF9Z1iDOB3ZExM6IqAB3Apuad4iIeyNiMl28D1ifYXnM+kLZNQhbJrIMiHXAU03Lu9J183k38IWm5VFJ2yTdJ+nSVgdIujrdZ9vExMRhF9isFyq1oCgoupPa+lxmTUydkPROYBy4oGn1yRGxW9KpwJclPRwRTzQfFxG3AbcBjI+P+9Nky8JCQ303uJPa+kGWNYjdwIlNy+vTdYeQdCFwA3BJRJQb6yNid/rfncBXgHMyLKtZzyw0UF9DIyDC81JbjrIMiK3ARkkbJA0DVwCH3I0k6RzgEyTh8GzT+mMljaSv1wA/ATR3bpstWwtNN9owO2lQvRclMmstsyamiKhKug64GygCt0fEdkk3A9siYjPwUeAo4K8lAXwvIi4BfgT4hKQ6SYh9aM7dT2bLVqUWC97BBIeOx7RYc5RZVjLtg4iILcCWOetubHp94TzH/TtwZpZlM8tLuR6sKLVXg6jUAoZ6USqzl/OT1GY91k4fxJBHdLU+4IAw67F2mo1GHBDWBxwQZj3W1l1MjU5qPwthOXJAmPVQRFCpL95J7SYm6wcOCLMeamegPpjTSW2WEweEWQ81nmto50lqcA3C8uWAMOuh2bkg2q1BOCAsRw4Isx5qfOEPLRIQRYmi3MRk+WorICT5oTWzLpipLz6bXIMH7LO8tVuD+FNJ90v6n5KOzrREZgOs3SYm8JDflr+2AiIi3gD8EsnorA9IukPSRZmWzGwAzbTZxASuQVj+2u6DiIjHgfcD7yWZt+GPJX1b0s9nVTizQVPppInJNQjLWbt9EGdJ+gPgUeBngLdFxI+kr/8gw/KZDZR2n4No7DPjGoTlqN3RXP8E+CTwuxEx1VgZEU9Len8mJTMbQI2hM9ppYhoqiP2eEMJy1G5AvBWYiogagKQCMBoRkxHxmcxKZzZgKvWgALQzxYObmCxv7fZBfBEYa1peka4zsw5U6sFQUaQTZC3IndSWt3YDYjQiXmospK9XZFMks8HVzkiuDY0ahOeltry0GxAHJJ3bWJD0Y8DUAvubWQszbcxH3TBcEHXArUyWl3b7IH6LZN7opwEBrwTenlWhzAZVo4mpHc0D9pXaDBWzbmorICJiq6TXAK9OVz0WETPZFctsMHXaxNQ4ZkWms8ebtdbJYH3nAWcB5wJXSvrlxQ6QdLGkxyTtkHR9i+3vkfSIpG9K+pKkk5u2XSXp8fTnqg7Kada3ZurBUJufOg/5bXlr6+8SSZ8BTgMeAmrp6gA+vcAxReBW4CJgF7BV0uaIeKRptweB8YiYlPTrwEeAt0s6DrgJGE/f54H02Bc6uTizflPppA/CkwZZztqtuI4DZ0Rnt1OcD+yIiJ0Aku4ENgGzARER9zbtfx/wzvT1m4F7ImJPeuw9wMXAX3bw/mZ9Z6bW3jAbcLAG4aepLS/tNjF9i6RjuhPrgKealnel6+bzbuALnRwr6WpJ2yRtm5iY6LB4Zr1XqUdbT1HDwaetyw4Iy0m7NYg1wCOS7gfKjZURcUk3CiHpnSS1lAs6OS4ibgNuAxgfH/enyPpaRHTUxDSS1jRm3MRkOWk3ID6whHPvJhkevGF9uu4Qki4EbgAuiIhy07E/NefYryyhDGZ9o5p+z7fbxDTkTmrLWbvzQXwV+A4wlL7eCnx9kcO2AhslbZA0DFwBbG7eQdI5wCeASyLi2aZNdwNvknSspGOBN6XrzJatTiYLAndSW/7aHe7714DPkXyZQ9If8HcLHRMRVeA6ki/2R4G7ImK7pJslNZqmPgocRfIQ3kOSNqfH7gF+jyRktgI3NzqszZarTiYLAigpeSrVNQjLS7tNTNeS3JX0NUgmD5J0wmIHRcQWYMucdTc2vb5wgWNvB25vs3xmfa+TyYIAJCXjMTkgLCft3sVUjohKY0FSieT5BDNrU6dNTI193cRkeWk3IL4q6XeBsXQu6r8G/l92xTIbPJ02MYGH/LZ8tRsQ1wMTwMPA/yBpNvJMcmYd6LSJqbGvaxCWl3YH66sD/yf9MbMlWGoTk5+ktry0OxbTk7Toc4iIU7teIrMBVVlCE9NQUUyWPS+15aOTsZgaRoHLgeO6XxyzwTWzhCamEdcgLEftPij3fNPP7oj4Q+Ct2RbNbLA0mphKHcz9M+ROastRu01M5zYtFkhqFJ7CxKwDjXGYJHdS2/LQ7pf87ze9rpIMu/GLXS+N2QDrZLKghuGCqAbUIyh0ECxm3dDuXUw/nXVBzAZduRaMFDtLiObxmEY7aZsy64J2m5jes9D2iLilO8UxG1yVWswO4d2u5mlHR7MolNkCOrmL6TwOjsb6NuB+4PEsCmU2iModzAXR4HmpLU/tBsR64NyI2A8g6QPAP0bEOxc8ysxmlWvBypGlNzGZ9Vq7v62vACpNy5V0nZm16XCbmMx6rd0axKeB+yX9bbp8KfCpTEpkNqDK9ejoITlwDcLy1e5dTB+U9AXgDemqX4mIB7MrltlgiYjkLqYl9kH4aWrLQycNoiuAfRHxR8AuSRsyKpPZwJlJh1PqtIlpqJj8101Mlod2pxy9CXgv8L501RDwF1kVymzQlOtJQnTcxFRwE5Plp90axM8BlwAHACLiaWBVVoUyGzTl9Au+4wfl3EltOWr3t7USEUE65LekldkVyWzwNGoAnfZBSGKo4BqE5aPdgLhL0ieAYyT9GvBF2pg8SNLFkh6TtEPS9S22v1HS1yVVJV02Z1tN0kPpz+a5x5otJ40aRKdNTOBpRy0/i97FpGToyb8CXgPsA14N3BgR9yxyXBG4FbgI2AVslbQ5Ih5p2u17wLuA32lxiqmIOLuNazDre+V6o4lpCQHhEV0tJ4sGRESEpC0RcSawYCjMcT6wIyJ2Aki6E9gEzAZERHwn3eYps2ygLWW60YaRYmE2YMx6qd0mpq9LOq/Dc68Dnmpa3pWua9eopG2S7pN0aasdJF2d7rNtYmKiw+KZ9U6jiWl0CTWIkYJmjzfrpXafpH498E5J3yG5k0kklYuzsioYcHJE7JZ0KvBlSQ9HxBPNO0TEbcBtAOPj4/4EWd86nD6I0ZJ4btqVbOu9BQNC0kkR8T3gzUs4927gxKbl9em6tkTE7vS/OyV9BTgHeGLBg8z6VCWdLGgpk/6MFF2DsHws1sT0dwAR8V3gloj4bvPPIsduBTZK2iBpGLiCg8OFL0jSsZJG0tdrgJ+gqe/CbLkp1+pL6n8AGC0WKNdcg7DeWywgmn+jT+3kxBFRBa4D7gYeBe6KiO2SbpZ0CYCk8yTtAi4HPiFpe3r4jwDbJH0DuBf40Jy7n8yWlcoSZpNrGCmKmTrU3FFtPbZYH0TM87otEbEF2DJn3Y1Nr7eSND3NPe7fgTM7fT+zflWudz7Ud0PjuHItWLHEWojZUiwWED8qaR9JTWIsfQ0HO6lXZ1o6swFRrnU+m1xD486ncj1Y0c1CmS1iwYCIiGKvCmI2yCpLmE2uoVGDmK7VAX8krXeW9htrZh0p1zqfLKih0XdRrroPwnrLAWHWA4fTBzE6W4NwQFhvOSDMMhYRyV1MS+yDGGnqgzDrJQeEWcZm6sktgIddg6j6WQjrLQeEWcaWOptcw3BBCPw0tfWcA8IsY43O5aU+KCeJ4aLcxGQ954Awy9hk+pf/itLSH3IbLYpp38VkPeaAMMvYZNp3MLbEGgR4wD7LhwPCLGNTaUCsGDqcGkQhfVDOrHccEGYZm0qbhlyDsOXGAWGWsclqMtR36TAG2nNAWB4cEGYZm6oGY4fRQQ1JJ7UDwnrNAWGWsalqnRWlw/uojaS3udbDIWG944Awy9hkF2oQjWcoKq5FWA85IMwyNlk7/BqEB+yzPDggzDI2Va0ztsRhNhpGHBCWAweEWYZm6sFMncOuQTSOn/KAfdZDDgizDDW+0McOMyAafRhTHm7DeijTgJB0saTHJO2QdH2L7W+U9HVJVUmXzdl2laTH05+rsiynWVZmH5I7zE7qRg1i0jUI66HMAkJSEbgVeAtwBnClpDPm7PY94F3AHXOOPQ64CXg9cD5wk6RjsyqrWVYaX+jd6KQWSYe3Wa9kWYM4H9gRETsjogLcCWxq3iEivhMR3wTm/ta/GbgnIvZExAvAPcDFGZbVLBONGsThjOQKUJAYLclNTNZTWQbEOuCppuVd6bquHSvpaknbJG2bmJhYckHNstL4i/9w+yAgqYW4icl6aVl3UkfEbRExHhHja9euzbs4Zi/T6KQePczbXAHGinJAWE9lGRC7gROblten67I+1qxvTFWDsaIo6PADYkWp4CYm66ksA2IrsFHSBknDwBXA5jaPvRt4k6Rj087pN6XrzJaVA9V6V5qXwE1M1nuZBUREVIHrSL7YHwXuiojtkm6WdAmApPMk7QIuBz4haXt67B7g90hCZitwc7rObFl5aabOqqFuBUTSSR0esM96pJTlySNiC7Blzrobm15vJWk+anXs7cDtWZbPLGv7K3VOWjXUlXONlQoEyXAbh/tchVk7lnUntVk/q0ewf6bO6i7WIMAPy1nvOCDMMnJgpk4Aq4a78zEbmx2PyU1M1hsOCLOM7J9J/tJfNVTsyvk83Ib1mgPCLCP7ZgOiu01MrkFYrzggzDKyv5IExOouNzG5BmG94oAwy8j+mToldecpaoChghgqOCCsdxwQZhnZX6mxariAuvAUdcNYqcCkm5isRxwQZhnZN1PvWgd1g5+mtl5yQJhlZH+l3rX+h4ZVQ4XZu6PMsuaAMMtAPaKrw2w0rB4usK9S93Ab1hMOCLMMHKjWqdO9W1wbVg8VqNSDcs0BYdlzQJhl4OAtrt3tgzg6Pd8+NzNZDzggzDKwNw2Io7vcB9Ho09hXcUBY9hwQZhl4sVwDDv7F3y2NGsm+Sq2r5zVrxQFhloG9lTpjJTHcpYfkGlaWRFGuQVhvOCDMMrC3Uut67QFAEquGCu6DsJ5wQJhlYG+l3vX+h4bVw0U3MVlPOCDMuiwi2FupcUwGNQg4+CyEWdYcEGZd9lK1Ti26fwdTw+rh5Gnqmh+Ws4w5IMy6bG+5cYtrNjWIo4eKBPCS+yEsY5kGhKSLJT0maYek61tsH5H0V+n2r0k6JV1/iqQpSQ+lPx/Pspxm3bQ37R84eiS7GgQcvJXWLCulrE4sqQjcClwE7AK2StocEY807fZu4IWIOF3SFcCHgben256IiLOzKp9ZVg4+JJdNDWLNaHLe56ZrnLwqk7cwA7KtQZwP7IiInRFRAe4ENs3ZZxPwqfT154CfVTcHzzfLwd5KjZUlMVTI5lf5qKECYyXxg6lqJuc3a8gyINYBTzUt70rXtdwnIqrAXuD4dNsGSQ9K+qqkN2RYTrOueqFcz6z2AMmzECeMlnh20k1Mlq1+7aR+BjgpIs4B3gPcIWn13J0kXS1pm6RtExMTPS+kWSvPTVc5fjS7gAB4xYoSE9NV6r6TyTKUZUDsBk5sWl6frmu5j6QScDTwfESUI+J5gIh4AHgC+OG5bxARt0XEeESMr127NoNLMOvMZLXOZDVYO5ZZ9x4AJ4wVqQU8P+1ahGUny4DYCmyUtEHSMHAFsHnOPpuBq9LXlwFfjoiQtDbt5EbSqcBGYGeGZTXriuemki/sNRnXIE5IA+hZ90NYhjL7MyciqpKuA+4GisDtEbFd0s3AtojYDPw58BlJO4A9JCEC8EbgZkkzQB24JiL2ZFVWs255bjr5ws46II4fLVIUPDtV47WZvpMdyTKtB0fEFmDLnHU3Nr2eBi5vcdzngc9nWTazLExM1xgpqOszyc1VlFgzWuT7k65BWHb6tZPabFl6brrKmrEivbhbe/1RQ+w+MMNM3R3Vlg0HhFmXRATPTdUyb15qOH31MNWA7+6f6cn72ZHHAWHWJQeqwVQtWDOa7R1MDSceNcRQAXbuq/Tk/ezI44Aw65IfpP0Ba8d6U4MoFcTJq4bZsa9C+HkIy4ADwqxLntxfoSRYt3KoZ+95+uph9lXqPOfnISwDDgizLtm5b4aTjhrKbAymVk5bnYTRf+51M5N1nwPCrAteLNfYU65x6urhnr7vquEi61aW+PYL5Z6+rx0ZHBBmXfBE2lHc64AAeM0xI0xM19jjZibrMgeEWRc8sbfCMcMFjuvRLa7NXn1MEkrfftG1COsuB4TZYZqYqrJz/wyvPW4kl/dfnTYzPfpC2XczWVc5IMwO03/8YIrhghhfO5ZbGc48bpSJ6RpPe+gN6yIHhNlheH66yqMvlDlnzShjpfw+TmccO8JwQXx9Yjq3MtjgcUCYLVFE8IXvvcRwUZx/Qn61B4DhonjdcSN8+8Uyk9V6rmWxweGAMFuibRPT7DpQ5WfXrWRlxqO3tuPcNaPUAv7lmcm8i2IDIv/farNl6HsvzXDv0wc4bfUQZ+bUOT3XmrES560d5cHnpj0+k3WFA8KsQ89PV/mbnfs4drjI205e1ZOhvdt1watWsma0yD9+dz8vlv1chB0eB4RZB56frnLH43spCC4/bTWjOXZMt1IqiEs3rKIW8FdP7GVyxv0RtnT99dtt1sca4RDAO04/mmNGev9QXDvWjJa47NTV7K/U+eud+6jU/GyELY0DwqwNz04dGg5rxnoz58NSrT9qiE0bVvH9ySqf27mP/TNubrLOOSDMFlCL4IGJKT792IsILYtwaNh49AhvPfkonj4wwycfeZF7dx/g2Sk/SGftWx6/6WY9VI/g+5NVdu6b4eE90+yt1Dll1RBvO3lVX9zO2onXHTfKupVDfHn3AbY+O8XXnp3irONHeOMPreSoZXYt1nuZBoSki4E/AorAJyPiQ3O2jwCfBn4MeB54e0R8J932PuDdQA34jYi4O8uy2mBqjE00351GlVrwfLnKxFSN56ZrPDdd5ZkDVabSdvv1K0tcuH4lp68e7qu7lTpx7EiRXzh1NVPVOvf9YIqtz06xfU+Z01YPs6JUYKiQPGh39HCRY0eKHDdSXHZBaNnILCAkFYFbgYuAXcBWSZsj4pGm3d4NvBARp0u6Avgw8HZJZwBXAK8FXgV8UdIPR4QbUufRapC2Vl2TMc/CovvOvs88799i7+Y19YCpap3JalCuBaNFMVYSY6UCo0VR6PDLtx7BdC2YTM85Va0TkbznSzN19pRrTExVmZiuUa4FRcFYsTD7nvUIXpqp82Ll4F0+RcHxo0VOP3qYDauH2bBqKNfhM7ptrFTgp9et5EePH2XbxBQ791Wo1INqHSr1Q//9jhku8IoVJValQVGLpLmtVk/C5PjRIquGCpQkqhFU64EkVg8VOHq4wIqhAvWAWj2YiZjtKC8VREmiWICiRETybxmz2+YP826J9P1q6XtDUpbiIu/d+IwFzP6uBSCgoOS/y/WPiPlkWYM4H9gRETsBJN0JbAKaA2IT8IH09eeAjyn5P7wJuDMiysCTknak5/uPbhdyslrn49tfWNKxLb8U5/0CXWRdzL/fQusHRWmez9V8173YjTkjRbF2tMgZx44wVhK1OkzV6kylYVKQeOWKEq87rsTasSJrRpO/njsNquXouNEibzrxqEPW1erB3kqdFytJTeqpl2aYmKrx5L4ZpCQ8ixIFwXQtCfmsJCFx6Lp2Bqltp0RB8sfKfERyrY19m8OgXQWS8jcmFhTZ/069ckWJd2w8uuvnzTIg1gFPNS3vAl4/3z4RUZW0Fzg+XX/fnGPXzX0DSVcDV6eLL0l6rIPyrQGe62D/5cTXtjz52pafvrmuX1r6oSfPt2FZd1JHxG3AbUs5VtK2iBjvcpH6gq9tefK1LT+Del0NWTaw7gZObFpen65ruY+kEnA0SWd1O8eamVmGsgyIrcBGSRskDZN0Om+es89m4Kr09WXAlyPpCdoMXCFpRNIGYCNwf4ZlNTOzOTJrYkr7FK4D7ia5zfX2iNgu6WZgW0RsBv4c+EzaCb2HJERI97uLpEO7ClybwR1MS2qaWiZ8bcuTr235GdTrAkCew9bMzFoZnJu8zcysqxwQZmbW0hEXEJJ+T9I3JT0k6Z8kvSpdL0l/LGlHuv3cvMvaCUkflfTttOx/K+mYpm3vS6/rMUlvzrGYSyLpcknbJdUljc/ZtqyvDZIhadLy75B0fd7lORySbpf0rKRvNa07TtI9kh5P/3tsnmVcKkknSrpX0iPp7+NvpusH4vpaOeICAvhoRJwVEWcD/wDcmK5/C8ndUhtJHr77s3yKt2T3AK+LiLOA/wTeBzBn2JKLgT9Nh0FZTr4F/Dzwz80rB+HamoakeQtwBnBlel3L1f8l+bdodj3wpYjYCHwpXV6OqsBvR8QZwI8D16b/VoNyfS9zxAVEROxrWlzJwafoNwGfjsR9wDGSfqjnBVyiiPiniGiM5XwfybMj0DRsSUQ8CTSGLVk2IuLRiGj1lPyyvzaahqSJiArQGJJmWYqIfya5I7HZJuBT6etPAZf2skzdEhHPRMTX09f7gUdJRngYiOtr5YgLCABJH5T0FMnT6Y0aRKuhQV42vMcy8d+BL6SvB+m65hqEaxuEa1jMKyLimfT194FX5FmYbpB0CnAO8DUG8PoalvVQG/OR9EXglS023RARfx8RNwA3pEOKXwfc1NMCLtFi15XucwNJVfizvSzb4Wrn2mz5i4iQtKzvrZd0FPB54LciYl/zCK6DcH3NBjIgIuLCNnf9LLCFJCD6fniPxa5L0ruA/wb8bBx8wKXvrws6+jdrtiyubRGDcA2L+YGkH4qIZ9Jm22fzLtBSSRoiCYfPRsTfpKsH5vrmOuKamCRtbFrcBHw7fb0Z+OX0bqYfB/Y2VRv7Xjo50/8GLomIyaZNgzxsySBcWztD0ix3zUPqXAUsyxphOhXBnwOPRsQtTZsG4vpaOeKepJb0eeDVQB34LnBNROxO//E/RnIHxiTwKxGxLb+SdiYdrmSEZLBDgPsi4pp02w0k/RJVkmrxF1qfpT9J+jngT4C1wIvAQxHx5nTbsr42AEn/FfhDDg5J88F8S7R0kv4S+CmSYbB/QFI7/zvgLuAkks/cL0bE3I7svifpJ4F/AR4m+f4A+F2Sfohlf32tHHEBYWZm7TnimpjMzKw9DggzM2vJAWFmZi05IMzMrCUHhJmZteSAsCOSpFo6ou92Sd+Q9NuSCum2cUl/vMCxp0h6xwLbXyXpc+nrd0n6WIdle1djlOF0+ZPLfAA/W6YG8klqszZMpSP6IukE4A5gNXBT+vzLQs/AnAK8Iz3mEJJKEfE0yRzrS/UukhFsnwaIiF89jHOZLZlrEHbEi4hnSYZ4vy59kv6nJP0DgKQL0prGQ5IelLQK+BDwhnTd/0r/4t8s6cvAl9Iaxrea3uJESV9J5wu4KT3vIftI+h1JH5B0GTAOfDY9/1h67Hi635WSHpb0LUkfbjr+pXQQym9Iuk/SwAwYZ/lxQJgBEbGT5EnmE+Zs+h3g2rS28QZgimS8/3+JiLMj4g/S/c4FLouIC1qc/nzgF4CzgMs1Z9KjOeX4HEnt5ZfS8081tqXNTh8GfgY4GzhP0qXp5pUkT8//KMm8Gb/W5qWbzcsBYbawfwNukfQbwDFNc27Mdc8CwyvcExHPp1/2fwP85BLLch7wlYiYSMvxWeCN6bYKyQRYAA+QNIOZHRYHhBkg6VSgxpyROCPiQ8CvAmPAv0l6zTynOLDA6eeOZxMkY0c1f/5GOyrwy800jeBbw/2L1gUOCDviSVoLfBz4WMwZnEzSaRHxcER8mGTk1dcA+4FVHbzFRem8xWMks439G8lAdidIOl7SCMkw7Q3znf9+4AJJa9KpSq8EvtpBOcw64r8y7Eg1JukhYIjkr/nPALe02O+3JP00yeid20lm6qsDNUnfIJmD+YVF3ut+kjkE1gN/0RglWNLN6bbdHBx2nvScH5c0BfyXxsp0voHrgXsBAf/oyZQsSx7N1czMWnITk5mZteSAMDOzlhwQZmbWkgPCzMxackCYmVlLDggzM2vJAWFmZi39f69/voqDsctMAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# T-distribution degree of freedom = 3\n",
    "rv = sp.stats.t(df=3)\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 20,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 20,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEICAYAAABF82P+AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAuJ0lEQVR4nO3deZTcd3nn+/en1t67JXdr6ZZktWQZW16wTVsQwGCCMfY4sRkCNzbDPWaGiYc59gm5JPfGTHIgxzm5B5JzITMTz4An45sNxmEgk9GAE18TjAkxBsm7ZVtWq7WvLan3pdbn/lG/NuV2q1Ut1a9re17n1NFvrXq61NVPfXeZGc4559x8kUoH4Jxzrjp5gnDOObcgTxDOOecW5AnCOefcgjxBOOecW5AnCOeccwsKNUFIukXSbkmDku5f5LpfkWSSBoqOfT64b7ekD4cZp3POubeKhfXEkqLAg8CHgMPADknbzeyVede1A58Fflp0bCtwJ3AF0At8X9KlZpY72+t1d3fbxo0by/5zOOdcPXvmmWdOmVnPQudCSxDANmDQzIYAJD0C3AG8Mu+63we+DPyfRcfuAB4xsxSwT9Jg8Hw/OduLbdy4kZ07d5YxfOecq3+SDpztXJhVTH3AoaL9w8GxN0i6DlhvZt9b6r3B/fdI2ilp5/DwcHmids45B1SwkVpSBPgK8Jvn+xxm9pCZDZjZQE/PgiUk55xz5ynMKqYjwPqi/XXBsTntwJXADyUBrAG2S7q9hHudc86FLMwSxA5gi6R+SQkKjc7b506a2ZiZdZvZRjPbCDwN3G5mO4Pr7pSUlNQPbAF+FmKszjnn5gmtBGFmWUn3AY8BUeBhM9sl6QFgp5ltX+TeXZK+RaFBOwvcu1gPJuecc+Wnepnue2BgwLwXk3POLY2kZ8xsYKFzPpLaOefcgjxBOLfM8nVSanf1L8xeTM65wEgqx5NHpxgaz5DOG+taYwysauayrmSlQ3PurDxBOBey3aMptu+fICK4cmUTyajYPZrib/dNcM1FGW5a10osokqH6dxbeIJwLkSvjhSSw9qWGB/d1EFbvFCr+761Lfzo2DRPn5hhIpPjo/0dRD1JuCrjbRDOheTYVIbvHpigrzXGnZd0vpEcACISN/a28uH1rewdz/A/90+Q87YJV2U8QTgXgulMnr/ZN0FrPMJHN3WQiC5cOri2u5mb1rXy+lia7+6f8AZsV1U8QThXZmbG3x+aZDqb56P9HbTEFv+YDfQ084HeFl4dTfO9A5OeJFzV8DYI58rslZEUr4+lubG3hTUtpX3E3rm6hZzBj45NE43ArevbCOYoc65iPEE4V0Yz2TzfPzxFX2uMbaual3Tvu9e0kDXjqeMzRCVuXtfqScJVlCcI58royaPTzOaMD69vI3Ief9xvWNNCLg8/PTlDVPDBPk8SrnI8QThXJsemMzx/epbre5pY1Xx+Hy1J3NjbQs6MncOzxCTe39viScJVhCcI58rAzHjiyDTNMfHetS0X9FyS+GBfKzmDp0/OEBHcsNaThFt+niCcK4N9ExkOThZGRSejF945UEEbRN6Mp07MEI+IX1hzYYnHuaXyBOHcBTIznjw6RVciwrUXNZXteSVxy/o2Mnl48tg0q5pjbO5MlO35nTsXHwfh3AXaN5HhxEyOd69pKft0GZK4dUMbq5qjbD8wwXja181yy8cThHMX6Knj07THI1yxIpyZWeMR8c/7O8jljR8cmQrlNZxbiCcI5y7A4ckMh6eybFvVHOpkeyuSUd61uoXXRtPsn0iH9jrOFQs1QUi6RdJuSYOS7l/g/GckvSTpeUk/lrQ1OL5R0kxw/HlJXwszTufO17OnZklGxdvL2PZwNu9a3UxXIsITR6aol6WCXXULLUFIigIPArcCW4G75hJAkW+a2VVmdg3wh8BXis7tNbNrgsdnworTufM1lcnz2miKq1YmzzoZXznFgp5MJ2ZyHJjIhP56zoVZgtgGDJrZkJmlgUeAO4ovMLPxot1WwL8WuZrx/OlZ8gbXdS9tSo0LccWKJK0x8fTJmWV7Tde4wkwQfcChov3DwbE3kXSvpL0UShC/XnSqX9Jzkp6UdMNCLyDpHkk7Je0cHh4uZ+zOLcrMeOHULBvb46xsii7b68YiYqCnmf0TGU5MZ5ftdV1jqngjtZk9aGabgd8Gfjc4fAzYYGbXAp8DvimpY4F7HzKzATMb6OnpWb6gXcM7MJlhPJNflraH+a7pbiIqeOnM7LK/tmssYSaII8D6ov11wbGzeQT4CICZpczsdLD9DLAXuDScMJ1bupdOp0hGxZYKDFxrjkXY0plg10iKXN5rZV14wkwQO4AtkvolJYA7ge3FF0jaUrR7G7AnON4TNHIjaROwBRgKMVbnSpbK5Xl9LMXlXUliFVpH+qqVTcxkjcFx7/LqwhPaVBtmlpV0H/AYEAUeNrNdkh4AdprZduA+STcBGWAEuDu4/X3AA5IyQB74jJmdCStW55bi9dE0mTxcuTKcgXGl6O+I0xaL8NKZFG/rqlwcrr6FOheTmT0KPDrv2BeKtj97lvu+A3wnzNicO1+vjaboSEToa63cVGYRictXJHj21CypXL4sEwQ6N5//Vjm3BLO5PPsmMlzWlaz49Ntv60qSM9g75mMiXDg8QTi3BINjafIGb+uq/Kyqfa0x2mIRXhtNVToUV6c8QTi3BK+NpOmIR+htqfxM+ZK4tCvB0HiadM57M7ny8wThXIlSuTz7JtJc2pWoePXSnLd1Jcga7PMJ/FwIPEE4V6LBsTQ5g8uqqNfQurY4yajY691dXQg8QThXotdG07THK9t7ab6oRH97nKGxjM/w6srOE4RzJUjl8gyNV1f10pxNHQkms3lOzvhqc668PEE4V4K945mqq16as6mj0KPKq5lcuXmCcK4Er4+maI2JdVVUvTSnLR5hTXOMIU8Qrsw8QTh3Dtm8MTSe4ZLO6qtemrOpM86RqSwz2XylQ3F1xBOEc+dwcDJDOm9s6ay+6qU5mzsSGLDPV5pzZeQJwrlz2DOWJh6Bi9vjlQ7lrNa2xGiOir1jXs3kyscThHOLMDMGx9JsbE8Qr9DU3qWISGzqSDA0kfburq5sPEE4t4gTMzkmMvmKLAy0VJs64sxkjWO+FKkrE08Qzi3i9bEUAi6piQRRiNHbIVy5eIJwbhF7RtP0tcZoiVX/R6U5Vujuus+7u7oyqf7feucqZDSVY3g2VxPVS3M2tsc5OpX12V1dWXiCcO4s9gQ9gi6twtHTZ7OxI06eQtdc5y5UqAlC0i2SdksalHT/Auc/I+klSc9L+rGkrUXnPh/ct1vSh8OM07mF7BlL090UZUUyWulQSrauNU5MsN+n/3ZlEFqCkBQFHgRuBbYCdxUngMA3zewqM7sG+EPgK8G9W4E7gSuAW4D/FDyfc8tiJpvn0GSmpqqXAGIRsa4tzn5vqHZlEGYJYhswaGZDZpYGHgHuKL7AzMaLdluBuYrTO4BHzCxlZvuAweD5nFsWe8fTGNRcgoBCO8Sp2RyTGZ92w12YMBNEH3CoaP9wcOxNJN0raS+FEsSvL/HeeyTtlLRzeHi4bIE7t2csTVsswtoqWFp0qTa2F5KaVzO5C1XxRmoze9DMNgO/DfzuEu99yMwGzGygp6cnnABdw8nmjX3jGTZ3xqt2cr7FrG6O0hyVVzO5CxZmgjgCrC/aXxccO5tHgI+c573Olc2hGpicbzGSuLg9zv5xX2XOXZgwE8QOYIukfkkJCo3O24svkLSlaPc2YE+wvR24U1JSUj+wBfhZiLE694a942liqu7J+c6lv72wytzpWV9lzp2/0CpYzSwr6T7gMSAKPGxmuyQ9AOw0s+3AfZJuAjLACHB3cO8uSd8CXgGywL1m5r/pLnRzk/NtaI9X9eR85zKX3PZPZOhurr12FFcdQv3NMbNHgUfnHftC0fZnF7n3D4A/CC86597qTCrHaDrP9auaKx3KBelKRulMRDg4mWGgxn8WVzkVb6R2rprsHS807G7uqL3urfOtb4tzaMrbIdz58wThXJG9wejprhoaPX02G9oK03+f8nYId548QTgXSOUKo6frofQAhQQBPi+TO3+eIJwL7JvIkAc21+Do6YV0JiK0xyMc8gThzpMnCOcCe8fSJKNiXWt99PqRxIa2OAcnvR3CnR9PEM5R6N66dzzNpvY4kRocPX02G9riTGeNMylvh3BL5wnCOeD4dJbprNVN9dKc9d4O4S6AJwjngMFgmc5NddJAPWdFMkJbLMKhyWylQ3E1yBOEcxTGP9TK2tNLIYn1bTEOTng7hFu6+vo0OHceJjN5jk9n66Z763wb2uNMZvOMpHx9CLc0niBcw9sbVC/Va4KYa4fw7q5uqTxBuIY3NJ6mPR5hVXPtj55eyEXJKM0xcXjKE4RbGk8QrqHlzNg/nmFTR20uDlQKSfS1xDky5Q3Vbmk8QbiGdnQqSypv9Ndp9dKcvtYYZ1I5ZrLeDuFK5wnCNbR942kEbGyr3cWBStEbjA73UoRbCk8QrqHtHU/T1xqjqc66t863tiWOgKPeDuGWoL4/Fc4tYiqT58RMru4Gxy0kERWrmqNegnBL4gnCNax9E/U5evps+lrjHJvOkvcBc65EoSYISbdI2i1pUNL9C5z/nKRXJL0o6R8kXVx0Lifp+eCxPcw4XWMaGs/QEhOr67R763x9rTHSeWN4xifuc6UJLUFIigIPArcCW4G7JG2dd9lzwICZXQ18G/jDonMzZnZN8Lg9rDhdY8qbsW88TX97om67t87X11poiD/i7RCuRGGWILYBg2Y2ZGZp4BHgjuILzOwJM5sOdp8G1oUYj3NvOD6dZSZnbOqo795LxToTEVpj8nYIV7IwE0QfcKho/3Bw7Gw+Dfxd0X6TpJ2Snpb0kYVukHRPcM3O4eHhCw7YNY6h8cK36Hof/1BMEr2tcY5OewnClaYqGqklfRIYAP6o6PDFZjYAfAL4Y0mb599nZg+Z2YCZDfT09CxTtK4e7JtIs7al/mZvPZe+1hgjqTxTGR8w584tzE/HEWB90f664NibSLoJ+B3gdjNLzR03syPBv0PAD4FrQ4zVNZCZbJ6jU9mGql6aM9cO4aUIV4qSEoSkq87juXcAWyT1S0oAdwJv6o0k6Vrg6xSSw8mi4yskJYPtbuA9wCvnEYNzb7F/IoPRON1bi61piRGRj6h2pSl1dfb/FPzB/jPgG2Y2dq4bzCwr6T7gMSAKPGxmuyQ9AOw0s+0UqpTagP8e9CQ5GPRYuhz4uqQ8hST2JTPzBOHKYmg8TVNUrG0p9de/fsQjYlVzjKOeIFwJSvqEmNkNkrYA/wp4RtLPgP/XzB4/x32PAo/OO/aFou2bznLfU8D5lFqcW5SZMTSepr89TqRBurfO19sS46Uzs+TNGvY9cKUpuQ3CzPYAvwv8NvB+4D9Iek3SR8MKzrlyOzmTYypb/7O3LqavNUYmD6dmfcCcW1ypbRBXS/oq8Crwi8Avm9nlwfZXQ4zPubJqtOk1FtI711Dt1UzuHEotQfxH4Fng7WZ2r5k9C2BmRymUKpyrCUPjGVY1R2mLN1b31mJdiQjNMfnMru6cSm2lu43C1Bc5AEkRoMnMps3sL0OLzrkySuXyHJ7MsG1Vc6VDqShJ9LbEODrtJQi3uFK/Rn0fKP5UtQTHnKsZByYy5Gns6qU5va1xTs3mmPUV5twiSk0QTWY2ObcTbLeEE5Jz4Rgaz5CIiL7WxuveOl9f0MX3mJci3CJKTRBTkq6b25H0DmAmnJCcKz8zY2gizcXtcaIR79q5JkiSXs3kFlPqV6nfoDCY7SggYA3wq2EF5Vy5nUnlGE/n+YXVjTe9xkKaohG6m6LeUO0WVepAuR2SLgPeFhzabWb+m+Vqxt5g9lZvf/i53pYYe8bSmFnDrInhlmYplbHXAxuDe66ThJn9RShROVdm+8bTXNQUpTPRGKvHlaK3Nc6LZ1KMpvOsSPr74t6qpAQh6S+BzcDzwNzwSwM8Qbiql8kbByczXNfdVOlQqkpv0A5xZCrjCcItqNQSxACw1cxXO3e15+BEhpx59dJ83U1REhFxdCrLlSsrHY2rRqX2YnqZQsO0czVnaCJNTLC+zRuoi0UkeltjHPaGancWpZYguoFXgllcixf1uT2UqJwro6HxQvfWmHdvfYu+1hhPHZ8hlcuTjDbu9CNuYaUmiN8LMwjnwjKSyjGSyvOOnsaeXuNs1rfGMWY4OpVt6Blu3cJK+spgZk8C+4F4sL2DwuR9zlW1fePB7K3t/sdvIWtbYwg45NVMbgGlTvf9a8C3KSwPCtAH/G1IMTlXNkPjGboSEVYkvfpkIclohFXNUY5M+ohq91alfmrupbAu9Di8sXjQqrCCcq4c8lbo3rqxPeEDwRaxri3O0ekMOe+k6OYpNUGkzCw9tyMpRmEcxKIk3SJpt6RBSfcvcP5zkl6R9KKkf5B0cdG5uyXtCR53lxinc284Pp0lnTcubvfeS4tZ3xonk4cTPi+Tm6fUBPGkpH8HNEv6EPDfgf+12A2SosCDwK3AVuAuSVvnXfYcMGBmV1OowvrD4N6VwBeBdwLbgC9KWlFirM4Bhem9ATZ499ZFzXX/nXu/nJtTaoK4HxgGXgL+DfAo515JbhswaGZDQenjEeCO4gvM7Akzmw52nwbWBdsfBh43szNmNgI8DtxSYqzOAXBwMkN3U5TWBl49rhSt8Qg9TVEOTHqCcG9W6mR9eeC/BI9S9QGHivYPUygRnM2ngb9b5N6++TdIuge4B2DDhg1LCM3Vu1zeODyV4aqVPr1GKTa0x3nx9Cy5vPl06O4NpfZi2idpaP6jXEFI+iSF6Tz+aCn3mdlDZjZgZgM9PT3lCsfVgWPTWTJ5vP2hRBe3FdohfH0IV2wpczHNaQI+Dpxr9pYjwPqi/XXBsTeRdBPwO8D7zSxVdO+N8+79YYmxOvdGdYm3P5RmQ1E7hE9J4uaUOlDudNHjiJn9MXDbOW7bAWyR1C8pAdwJbC++QNK1FMZW3G5mJ4tOPQbcLGlF0Dh9c3DMuZIcnMiwqjlKc8zbH0rRFIuwpjnG/on0uS92DaPU6b6vK9qNUChRLHqvmWUl3UfhD3sUeNjMdkl6ANhpZtspVCm1UVitDuCgmd1uZmck/T6FJAPwgJmdWcoP5hpXNm8cmcpwjU/vvSSbOuL85MQMs9k8TZ5YHaVXMf0/RdtZCtNu/G/nusnMHqXQ46n42BeKtm9a5N6HgYdLjM+5NxydypI1b39Yqs2dCZ46McO+iQyXr0hWOhxXBUrtxfSBsANxrlwOTKYRhQFgrnRrW2I0RcXe8bQnCAeUXsX0ucXOm9lXyhOOcxfu4GSG1c0xryZZoojEpo4EQ+O+TrUrKPUTNAD8WwpjEfqAzwDXAe3Bw7mqkMkbR6ayXr10njZ3xJnOmnd3dUDpbRDrgOvMbAJA0u8B3zOzT4YVmHPn48hkhrx599bztbkjQUTw2kiKPq+ia3illiBWA8X939LBMeeqyoHJDALWtZX63ccVa4pF6G+Ps3u0UM3kGlupn6K/AH4m6X8E+x8B/jyUiJy7AAcnM6xtifnymRfgsq4ke8cnOTadpddLEQ2t1IFyfwD8S2AkePxLM/u/wwzMuaVK54xj3v5wwbZ0BtVMoz5ortEt5WtWCzBuZv8eOCypP6SYnDsvh6cy5PH2hws1V830ykiKvFczNbRSJ+v7IvDbwOeDQ3Hgr8IKyrnzcWAiQ0SFFdLchbnqoiYmM3n2jfsU4I2s1BLEPwduB6YAzOwo3r3VVZmDkxl6W2LEfbrqC7alI0FzVLx0ZrbSobgKKjVBpK3QpcEAJLWGF5JzSzeby3N8OssGb38oi2hEbF2ZZM9YmplsvtLhuAopNUF8S9LXgS5JvwZ8n6UtHuRcqA5NZjAK6xq48rh6ZRM5g5fPpM59satL5+zmqsJ4+78GLgPGgbcBXzCzx0OOzbmSHZzIEBU+uKuMVrfE6G2J8dypWQZ6mnzqjQZ0zgRhZibpUTO7isLa0M5VnQOTGfpa48S8/aGsru1u4nsHJzk4meHi9kSlw3HLrNQqpmclXR9qJM6dp5lsnpMzOR//EILLViRpiornTnljdSMqdST1O4FPStpPoSeTKBQurg4rMOdKddCXFw1NPCKuWpnkmeFZJjN52uI+Qr2RLJogJG0ws4PAh5cpHueW7OBkhngEelt8/qUwXNvdzI7hWV48Pcu717RUOhy3jM71deBvAczsAPAVMztQ/Ag9OudKcHCi0P4Q9faHUKxsinJxW5znT836yOoGc64EUfyJ27TUJ5d0i6TdkgYl3b/A+fdJelZSVtLH5p3LSXo+eGxf6mu7xjCdyTM8m/PurSG7tqeJ8UyeIR9Z3VDOVSa3s2yfk6Qo8CDwIeAwsEPSdjN7peiyg8CngN9a4ClmzOyapbymazxvtD94A3WotnQmaItFeO7UDJd0em+mRnGuBPF2SeMUShLNwTb8vJG6Y5F7twGDZjYEIOkR4A7gjQRhZvuDcz5U052XA5MZEhGxxtsfQhWVuLo7yVPHZxhN5ehKRisdklsGi1YxmVnUzDrMrN3MYsH23P5iyQEKS5MeKto/HBwrVZOknZKelvSRhS6QdE9wzc7h4eElPLWrFwcmMqxvixH1QVyhu+aiJgS8cNq7vDaKau6zdrGZDQCfAP5Y0ub5F5jZQ2Y2YGYDPT09yx+hq6iJTI4zqZx3b10mHYkomzsTvHB6llzeG6sbQZgJ4giwvmh/XXCsJGZ2JPh3CPghcG05g3O17+BEof3BR/gun+u6m5jOGrvHfDGhRhBmgtgBbJHULykB3AmU1BtJ0gpJyWC7G3gPRW0XzkGhgToZFauavT58ufS3x+lMFBqrXf0LLUGYWRa4D3gMeBX4lpntkvSApNsBJF0v6TDwceDrknYFt18O7JT0AvAE8KV5vZ+cC9of4kS8/WHZSOLa7iYOTWY5NZOtdDguZKF2/TCzR4FH5x37QtH2DgpVT/Pvewq4KszYXG0bTeUYTecZ6PH2h+V21comnjw6zcsjKW5s9t5j9ayaG6mdO6t9E4U68P4OTxDLrTVeWLP61ZEU5iOr65onCFeThsYzdCQirPT++BVx+YokY+k8R6e9mqmeeYJwNSdnxoGJDJvaE76ITYVs6UoQFbw64qvN1TNPEK7mHJ3Kks6bVy9VUFM0wuaOBK+NpL2aqY55gnA1Z994GoEvEFRhl3YlmMzmOebVTHXLE4SrOUMTGfpaYzRF/de3kjZ3JBAw6IPm6pZ/wlxNmc7mOT6dpb/DR09XWnMswrq2GHs8QdQtTxCupuwP1iPo9+qlqrClM8nwbI7RVK7SobgQeIJwNWVoIk1T1Kf3rhZbgrUhvBRRnzxBuJphZuwfz9Df7tNrVIsVySjdTVFvh6hTniBczTg+k2Uym2eTtz9UlS2dCQ5OZpjN+rpf9cYThKsZr48Wurf6kpfV5ZLOBAbsHfdSRL3xBOFqxp6xNOvb4jTH/Ne2mvS2xGiJyauZ6pB/0lxNODOb49Rsjku99FB1JHFJZ4Kh8Qw5H1VdVzxBuJrw+lhhzp8tXZ4gqtElHQlSeePwZKbSobgy8gThasKrIynWtsToTPjsrdVoY3uCiGDvuCeIeuIJwlW907NZTszkuHxFstKhuLNIRMWGtrg3VNcZTxCu6r0STCl9+QqvXqpmmzsSnPZR1XUl1AQh6RZJuyUNSrp/gfPvk/SspKykj807d7ekPcHj7jDjdNXLzHh1JM2Gtjjtca9eqmabg/EpXoqoH6ElCElR4EHgVmArcJekrfMuOwh8CvjmvHtXAl8E3glsA74oaUVYsbrqdWw6y5lUjiu8eqnqrWyKsiIZYcgTRN0IswSxDRg0syEzSwOPAHcUX2Bm+83sRWD+EMwPA4+b2RkzGwEeB24JMVZXpV44PUs8Apd59VJN2NyR4MBEhkzeu7vWgzATRB9wqGj/cHCsbPdKukfSTkk7h4eHzztQV53SuUL10mVdSZK+9kNN2NyRIGtwcMJ7M9WDmv7UmdlDZjZgZgM9PT2VDseV2WujKdJ54+0XNVU6FFei9W1x4hFvh6gXYSaII8D6ov11wbGw73V1wMx49tQsFzVF6Wv1qb1rRSwiNrYnGBz3tarrQZgJYgewRVK/pARwJ7C9xHsfA26WtCJonL45OOYaxJGpLMens7yjuwn51N41ZXNHgvF0nuFZ7+5a60JLEGaWBe6j8If9VeBbZrZL0gOSbgeQdL2kw8DHga9L2hXcewb4fQpJZgfwQHDMNYidwzMko+LKlV69VGsu8UWE6kaoZXczexR4dN6xLxRt76BQfbTQvQ8DD4cZn6tOY+kcu0fTXL+qmUTUSw+1pi0eobelsFb1e9a0VDocdwFqupHa1aefnphBwDt6vPRQq7Z0Jjg+nWU87dVMtcwThKsqU5k8L56e5cqVSZ+Yr4bNzbrra0TUNk8Qrqr87OQMOYN3rfaqiVp2UTLKymSU3aOeIGqZJwhXNSYzeZ4ZnuHyFUlWNnnpoZZJ4rIVhbWqpzK+VnWt8gThqsZTx6fJG9yw1ksP9eDyriQG7B5NVToUd548QbiqMJrK8fypWd7e3cSKpJce6kFPc4zupiiveoKoWZ4gXFX4x2PTRATvXtNc6VBcGV3WleTQZJYJ781UkzxBuIo7OZNl10iKd/Q0+5oPdeaKlYVp2l8+46WIWuQJwlXcj45Ok4yId6320kO9WZGMsr4txotnZn1uphrkCcJV1IGJNIPjad61upnmmP861qOrVjYxkspzeCpb6VDcEvkn0lWMmfGDI1N0xCMMrPLSQ726rCtJIiJeOD1b6VDcEnmCcBXz8pkUJ2ZyvL+3hXjE51yqV4mouHJlkldHUkz6mIia4gnCVUQmb/zo2DRrWmJs9fWm695ATzM5g+dOzVQ6FLcEniBcRew4OcNEJs8H+1p9vYcGsLIpyuaOOM+dmvX1qmuIJwi37CYzeZ4+McOlnQnWt8UrHY5bJu9c3cJ01njulLdF1ApPEG7Z/fjYNNm8cWNva6VDcctoQ1ucje1xnj4xTSrnbRG1wBOEW1bDM1leOD3LtT1NPiFfA3rf2kIpYsdJL0XUAk8QbtmYGY8dmiQZFe/1lcYaUm9rnLd1JXj6xDQjKZ9+o9qFmiAk3SJpt6RBSfcvcD4p6a+D8z+VtDE4vlHSjKTng8fXwozTLY+Xz6Q4PJXlA72tPiiugd3U10pE4rFDkz66usqF9imVFAUeBG4FtgJ3Sdo677JPAyNmdgnwVeDLRef2mtk1weMzYcXplsdsNs8TR6fobYlx9UXerbWRtSei3Njbwv6JDM94g3VVC/Nr3DZg0MyGzCwNPALcMe+aO4A/D7a/DXxQ3uexLv3o2DQzWePm9W3erdVxbXcTmzvi/ODIFEenMpUOx51FmAmiDzhUtH84OLbgNWaWBcaAi4Jz/ZKek/SkpBsWegFJ90jaKWnn8PBweaN3ZXNsKsOzp2a5rqeJNS2xSofjqoAkfunidtriEf5m3wRjPh14VarWiuBjwAYzuxb4HPBNSR3zLzKzh8xswMwGenp6lj1Id26ZvPHdg5O0xyO+Upx7k+ZYhI9v6iCTN/56cJxpn4aj6oSZII4A64v21wXHFrxGUgzoBE6bWcrMTgOY2TPAXuDSEGN1IfnR0SlOz+a4dUMbTdFq/T7iKqWnOcavbOpgPJ3jvw2OMZ31JFFNwvzE7gC2SOqXlADuBLbPu2Y7cHew/THgB2ZmknqCRm4kbQK2AEMhxupCMDiWZsfwLNd2N7GpI1HpcFyV2tAW52ObOhhJ5fhvezxJVJPQEkTQpnAf8BjwKvAtM9sl6QFJtweX/VfgIkmDFKqS5rrCvg94UdLzFBqvP2NmZ8KK1ZXfWDrHdw9MsKo5yi/2+Yhpt7iNHQl+JUgSjwyOMeNJoiqoXvohDwwM2M6dOysdhgPSOeOv9owylspz99u6fMS0K9m+8TTfGRpnZVOUuy7p9PEyy0DSM2Y2sNA5f/ddWeXN+F8HJhieyXH7xnZPDm5J+oOSxOnZQpuElyQqyxOEKxsz4+8PTbJnLM0H+1rZ3OntDm7p+jsSfMyTRFXwBOHKYm750BdPp3j3mmZfQtRdkOKShLdJVI4nCFcWT52YYcfwLO/oaeIGn4jPlcGmIEmcCpKETxG+/DxBuAtiZvz42DT/eGyaK1YkuclXiHNltKkjwUf7OxieyfGdoQmyvhrdsvIE4c6bmfHDo9P8+Pg0V65MctvFPs+SK7/NnQluu7iNg5MZtu+fIF8nPS9rgScId17yZjx+eIqfnpzh2u4mbtvQRsSTgwvJFSub+GBfK6+PpX2a8GXkM6e5JUvl8mzfP8He8QzbVjXzgd4WLzm40F2/qpnpbJ6fnJihNRbhfb5kbeg8QbglGU3l+PbQOKdnc9y8rpXrery3kls+hSVL8zx1YoZEVLxrtXeICJMnCFey10ZT/P3BSQDuvKSDi9t9nINbXpL48Po20rlC+1c2D+9Z0+wl2JB4gnDnNJ7O8YMjU7w2mmZNS4w7NrazIukjpF1lRCR+eWM70YOT/Pj4NBOZHDevbyPqSaLsPEG4sxpN5dgxPMMLwbKQN6xt4V2rm/2D6CouInHbhjY64hGeOjHDqdkcv3xxO13+xaWsPEG4N8mbcWAiw4unZ3ltNI0EW1ckee+aFv/wuaoiiff1ttLdHOOxg5M8/Noo71nTzEBPM9GIf4kpB08QDjPj6HSWXWdSvDaaYjprJKNi26pmBnqaaE94YnDVa+uKJL0tMR4/PMkTR6d5ZniW61c1c+XKpM8Ge4E8QTSwkzNZXh1J8cpIirF0npgKg5K2rkiyuSNBzL+FuRrRlYzy8c2d7BtP80/Hp/mHI1M8cWSKTR0Jtq5Msqk9TpMniyXzBNFA8mYcmcoyOJZmcDzN6dkcAvrb47x3TQuXdiVI+rKgrob1dyTo70hwYjrLrpEUr46kGNyfRsDalhgbO+Ksb42ztjXmS+CWwBNEncnljalsnqlMnslsnslMnlOzOU5MZzk5kyOdNyLA+rY471jXxGVdSVri/kFx9WV1S4zVLTFu7G3h6FSWfRNp9k9k+MnxGZ5iBoDupig9TVEuaorR3RSlKxmlIxGhOSrvNhvwBFFjzIzJbJ7RVJ7RVI7RdK6wnc4xmsoxlX3rFASJiFjVHOXKlUk2tMXZ2BH3b0+uIUQk1rXFWdcW54a1hVkAjk1nOTKV5ehUhqPTWV4dTb/pnngEOhJROuORwr+JCB2JCJ2JQgJpi0caZlqZUBOEpFuAfw9EgT81sy/NO58E/gJ4B3Aa+FUz2x+c+zzwaSAH/LqZPRZmrNUklcszli4kgLF0nrF0jpFgezSVozgHCGhPROhKRNncmaAzEaUtFqE1HqE1JlrjEdrjEf9G5ByQjEbY2J5gY9Egz3TOOJPKMZbOMR583ub+PTadZSb35i9dUUFPc4zVzVFWNxdKKhcloyTrsOQRWoKQFAUeBD4EHAZ2SNpuZq8UXfZpYMTMLpF0J/Bl4FclbQXuBK4AeoHvS7rUzHJhxVvMzDDADAzIGxhG3iBnhbr8wrYF+7xphknN2xBv/qXJmTGdzTOdNWaCf8fTOUbTecZSubf8QiYioisZYWUyyqaOBF2JCF3JKF3Btxvv0ufc+UtExZqWGGtaFv5zmM4VPp9j6TzjmRxnZnOcnMmxezTNC6dTP3+eiApVVDGRiIh4RMQihe2oIBYRUYlYBKL6+bFYcGzu+nhExCMUbYuYqEjyCbMEsQ0YNLMhAEmPAHcAxQniDuD3gu1vA3+iwrtwB/CImaWAfZIGg+f7SbmDnM7k+c+vnMEM8vw8KSynmH5eCljTlaQrWSjOdiUidCajXifqXAUloqK7OUb3vGnHzIyJTJ4TM1lGUvk3kshsLs9Uxsjk82TyRjpvhS+T+cLfmAslQAr+DbbXtsT5xJbOMjz7m4WZIPqAQ0X7h4F3nu0aM8tKGgMuCo4/Pe/evvkvIOke4J5gd1LS7vKEviy6gVOVDqKCGv3nB38PGv3nhzK+B//i/G+9+GwnarqR2sweAh6qdBznQ9JOMxuodByV0ug/P/h70Og/P1T/exBmV5YjwPqi/XXBsQWvkRQDOik0Vpdyr3POuRCFmSB2AFsk9UtKUGh03j7vmu3A3cH2x4AfWGGpqO3AnZKSkvqBLcDPQozVOefcPKFVMQVtCvcBj1Ho5vqwme2S9ACw08y2A/8V+MugEfoMhSRCcN23KDRoZ4F7l6sH0zKqyaqxMmr0nx/8PWj0nx+q/D2Qr+3qnHNuIT6c1jnn3II8QTjnnFuQJ4gqIOk3JZmk7krHspwk/ZGk1yS9KOl/SOqqdEzLQdItknZLGpR0f6XjWW6S1kt6QtIrknZJ+mylY6oESVFJz0n6bqVjORtPEBUmaT1wM3Cw0rFUwOPAlWZ2NfA68PkKxxO6oilobgW2AncFU8s0kizwm2a2FXgXcG8DvgcAnwVerXQQi/EEUXlfBf4vln+Gj4ozs//PzLLB7tMUxrvUuzemoDGzNDA3BU3DMLNjZvZssD1B4Y/kW2ZKqGeS1gG3AX9a6VgW4wmigiTdARwxsxcqHUsV+FfA31U6iGWw0BQ0DfXHsZikjcC1wE8rHMpy+2MKXwzLMT1TaGp6qo1aIOn7wJoFTv0O8O8oVC/VrcV+fjP7n8E1v0Oh2uEbyxmbqyxJbcB3gN8ws/FKx7NcJP0ScNLMnpF0Y4XDWZQniJCZ2U0LHZd0FdAPvBDM1LoOeFbSNjM7vowhhupsP/8cSZ8Cfgn4oDXGoByfRgaQFKeQHL5hZn9T6XiW2XuA2yX9M6AJ6JD0V2b2yQrH9RY+UK5KSNoPDJhZw8xuGSwo9RXg/WY2XOl4lkMw59jrwAcpJIYdwCfMbFdFA1tGwZT+fw6cMbPfqHA4FRWUIH7LzH6pwqEsyNsgXCX9CdAOPC7peUlfq3RAYQsa5eemoHkV+FYjJYfAe4D/HfjF4P/9+eDbtKsyXoJwzjm3IC9BOOecW5AnCOeccwvyBOGcc25BniCcc84tyBOEc865BXmCcA1JUi7oXrlL0gvBjLqR4NyApP+wyL0bJX1ikfO9kr4dbH9K0p8sMbZPSeot2v/TBp3MzlWYj6R2jWrGzK4BkLQK+CbQAXzRzHYCOxe5dyPwieCeN5EUM7OjFNZYP1+fAl4GjgKY2b++gOdy7rx5CcI1PDM7CdwD3KeCG+fm6Jf0/qLBXM9Jage+BNwQHPs/gm/82yX9APiHoITxctFLrJf0Q0l7JH0xeN43XSPptyT9nqSPAQPAN4Lnbw7uHQiuu0vSS5JelvTlovsnJf1BUBp6WtLqsN83V/88QTgHmNkQEAVWzTv1W8C9QWnjBmAGuB/4RzO7xsy+Glx3HfAxM3v/Ak+/DfgV4Grg43N/7M8Sx7cplF7+RfD8M3PngmqnLwO/CFwDXC/pI8HpVuBpM3s78CPg10r80Z07K08Qzi3un4CvSPp1oKto/Yr5HjezM4ucOx38sf8b4L3nGcv1wA/NbDiI4xvA+4JzaWBuZbJnKFSDOXdBPEE4B0jaBOSAk8XHzexLwL8GmoF/knTZWZ5iapGnnz+fjVGY3rz489e0pIDfKlM0G24Ob190ZeAJwjU8ST3A14A/mT/luKTNZvaSmX2ZwsyrlwETFCYZLNWHJK2U1Ax8hEKp5ASwStJFkpIUpjyfc7bn/xnwfkndwdKldwFPLiEO55bEv2W4RtUs6XkgTuHb/F9SmHp8vt+Q9AEKK3/torDqXR7ISXoB+DNg5Byv9TMKax+sA/4q6CWFpAeCc0eA14qu/zPga5JmgF+YO2hmxyTdDzwBCPje3KJLzoXBZ3N1zjm3IK9ics45tyBPEM455xbkCcI559yCPEE455xbkCcI55xzC/IE4ZxzbkGeIJxzzi3o/wce0F0Q54SqugAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# T-distribution degree of freedom = 30, 정규분포와 가까워짐\n",
    "rv = sp.stats.t(df=30)\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### F 분포 (F Distribution)\n",
    "\n",
    "분산분석 등에서 사용되는 확률 분포\n",
    "\n",
    "확률변수 $Y_1$, $Y_2$는 서로 독립이고, 각 카이제곱분포를 따를 때($Y_1 \\sim x^2(n_1)$, $Y_2 \\sim x^2(n_2)$),\n",
    "\n",
    "$$F = \\frac{\\frac{Y_1}{n_1}}{\\frac{Y_2}{n_2}}$$\n",
    "\n",
    "의 확률분포를 자유도가 $n_1$, $n_2$인 F분포 $F(n_1, n_2)$"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 21,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[Text(0.5, 0, 'Distribution'), Text(0, 0.5, 'Frequency')]"
      ]
     },
     "execution_count": 21,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEGCAYAAABo25JHAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkuklEQVR4nO3de5Skd13n8fenqrqre+63DgmZyQ1DYpBbHAKKCMrFIGviBTCIu4BKlpUcZZFdg3oiJ3vcY/SI6yW7EBEFhA2QVRxl2BAQgsshMAMGcifDEMjM5NKZ+/Stbt/943mqp9Lp6q7urqcuXZ/XOZ2uep6nqn7zdPr59O/y/H6KCMzMbHDlul0AMzPrLgeBmdmAcxCYmQ04B4GZ2YBzEJiZDbhCtwuwVNu2bYvzzjuv28UwM+srX//615+IiLH59vVdEJx33nns3bu328UwM+srkr7XbJ+bhszMBpyDwMxswDkIzMwGnIPAzGzAOQjMzAacg8DMbMA5CMzMBpyDYIk8bbeZrTYOgiX40qEJPnD/MU6Uqt0uiplZ2zgIluChk2UOT1f52IPHmSjXul0cM7O2cBC0KCIYn66wY12BY6Uadx+Z7naRzMzawkHQouOlGuUaPGvzCOuGcjw+5eYhM1sdHAQtGp+uADA2mmdsJD/73Mys3zkIWjSe1gC2jeQZGy1weLpKzSOIzGwVcBC06InpKhuGcxTzOc4YzVMNODLt5iEz638OghaNT1UYG8kDMDaSLOMw7iAws1XAQdCCai04PF1lbDQJgK0jeUQSDmZm/c5B0IJjpSo1kv4BgEJObB3Je+SQma0KDoIWTFaSTuG1hdOnyyOHzGy1yDQIJF0u6QFJ+yRd2+SY10u6V9I9kj6WZXmWa6qS3EU82hAEm0fynCjVqHrkkJn1ucwWr5eUB24EXgkcAPZI2hUR9zYccyHwbuDFEXFU0hlZlWclpqrJxX4kr9ltG4fzBHCyVGNTMd+lkpmZrVyWNYLLgH0RsT8iSsDNwJVzjnkrcGNEHAWIiMczLM+yTc/WCBqDIDl1xz0BnZn1uSyD4Gzg4YbnB9JtjZ4JPFPSlyXdIeny+d5I0tWS9kraOz4+nlFxm5uqBjlgOPfkGgEkU0+YmfWzbncWF4ALgZcBbwD+StKmuQdFxE0RsTMido6NjXW2hMB0JRgtCOl0EKwfSk7dCQeBmfW5LIPgILCj4fn2dFujA8CuiChHxHeBb5MEQ0+ZqtYYKTz5VBVyYt1Qzk1DZtb3sgyCPcCFks6XNAxcBeyac8ynSGoDSNpG0lS0P8MyLctUJRht6Ciu2zicc9OQmfW9zIIgIirANcCtwH3AJyLiHknXS7oiPexW4LCke4EvAP8lIg5nVablmqo8tUYAST+BVyszs36X2fBRgIjYDeyes+26hscBvDP96lnT1eDMeWoEG4Zz3H+sRkQ8qf/AzKyfdLuzuC9MVWpPupmsbuNwjlrAKS9baWZ9zEGwiHItqARN+gg8hNTM+p+DYBH1m8lGCvM3DYFvKjOz/uYgWER9eonR/FNP1YahpEbgewnMrJ85CBYxtUCNYDgvinlx0n0EZtbHHASLmF6gRgDJHcYOAjPrZw6CRUylaxGMzlMjgCQIPGrIzPqZg2AR09W0aahJjWCdawRm1uccBIuYqgR5wVCTM7V+KMdEuUbNC9SYWZ9yECxiqlJjNJ9reufw+uEcAUy4VmBmfcpBsIipasw7YqhuXVpVcPOQmfUrB8EiStWgOM9dxXXr03sJHARm1q8cBIso1+JJK5PNVV+gxiOHzKxfOQgWUaoFQwsEwZqCyMk1AjPrXw6CRZRqwfACTUOSWFfIcdLTTJhZn3IQLKJcXbhpCJKRQ24aMrN+5SBYxGJNQ+CbysysvzkIFlCNoBos2DQEnmbCzPqbg2AB5XTCucVqBOuHcpRqwUzVYWBm/cdBsIBSLQmCxfoIfFOZmfUzB8ECyi0GQf2mslMeOWRmfchBsIB6jSC9zje1ftg1AjPrXw6CBZSqbhoys9Uv0yCQdLmkByTtk3TtPPvfLGlc0p3p169lWZ6lql/XFwuCoZwYycsjh8ysLxWyemNJeeBG4JXAAWCPpF0Rce+cQz8eEddkVY6VON00tHAQgJesNLP+lWWN4DJgX0Tsj4gScDNwZYaf13blFpuGwDeVmVn/yjIIzgYebnh+IN021y9I+pakWyTtmO+NJF0taa+kvePj41mUdV6tDh+F9KYyjxoysz7U7c7ifwLOi4jnALcBH5rvoIi4KSJ2RsTOsbGxjhVutmmolRrBcI6JipesNLP+k2UQHAQa/8Lfnm6bFRGHI2ImffoB4IczLM+SlavJesX5FmsEgdclMLP+k2UQ7AEulHS+pGHgKmBX4wGSzmp4egVwX4blWbJWJpyrm72pzEFgZn0ms1FDEVGRdA1wK5AHPhgR90i6HtgbEbuA35B0BVABjgBvzqo8y7HY6mSNfC+BmfWrzIIAICJ2A7vnbLuu4fG7gXdnWYaVWGxRmkbrHQRm1qe63Vnc08rV1puG6ktWeuSQmfUbB8ECSktoGpLkewnMrC85CBZQqkVLdxXX+e5iM+tHDoIFLKWzGLxSmZn1JwfBAkotLFzfKGkaqhK+qczM+oiDYAHlGgwt4QytH8pRrsFMzUFgZv3DQdBERCxp+CicvpfAI4fMrJ84CJpodS2CRr672Mz6kYOgifISJpyr85KVZtaPHARNzE5BvYymIQeBmfUTB0ET9fWKl1Ij8JKVZtaPHARNlJewKE0j31RmZv3GQdDEcvoIwEtWmln/cRA0UQ+CwjJqBB4+amb9xEHQRCW9li/lhjJIagRestLM+omDoIlyLK9paP2wl6w0s/7iIGhiJX0E4CAws/7hIGiisuw+guTuYncYm1m/cBA0MdtZvLQcmF2y0jUCM+sXDoIm6jOPSktLgvqSla4RmFm/cBA0UanFkpuFIF2yspDjpIeQmlmfcBA0Ua4FQ0usDdSt80plZtZHHARNlGux5BFDdeuHfXexmfWPTINA0uWSHpC0T9K1Cxz3C5JC0s4sy7MU5VpQWObZcY3AzPpJS5c6Sc9e6htLygM3Aq8GLgHeIOmSeY5bD/wm8NWlfkaWKrWl30NQt34oR6kWzFQdBmbW+1r9m/d/SvqapF+XtLHF11wG7IuI/RFRAm4GrpznuP8G3ABMt/i+HbGipiEPITWzPtJSEETES4A3AjuAr0v6mKRXLvKys4GHG54fSLfNknQpsCMiPt16kTtjJUHgBWrMrJ+03AoeEQ8Cvwf8NvBS4M8l3S/p55fzwZJywHuB32rh2Ksl7ZW0d3x8fDkft2SVWEmNIL272ENIzawPtNpH8BxJfwrcB/wk8DMR8YPp4z9t8rKDJDWIuu3ptrr1wA8BX5T0EPAiYNd8HcYRcVNE7IyInWNjY60UecXKNVbUWQxuGjKz/lBo8bi/AD4A/E5ETNU3RsQhSb/X5DV7gAslnU8SAFcBv9Tw2uPAtvpzSV8E3hURe5f0L8jISpqGhvOimJebhsysL7QaBK8BpiKiCrPNOiMRMRkRH5nvBRFRkXQNcCuQBz4YEfdIuh7YGxG72lD+zKwkCAA2DOU44aYhM+sDrQbB54BXAKfS52uAzwI/utCLImI3sHvOtuuaHPuyFsuSuWoEtVj6zKONNgznOFGutrFUZmbZaLUVfCQi6iFA+nhNNkXqvsoy1yJotHE47xqBmfWFVoNgIh3qCYCkHwamFji+r5WXuUxlow3DOaarvqnMzHpfq01D7wA+KekQIOBM4BezKlS3zS5Ks8xJ5wA2NAwhLY56Sicz610tBUFE7JF0MXBRuumBiChnV6zuWu4ylY02DCcX/+OlGttG21IsM7NMtFojAHgBcF76mkslEREfzqRUXdbOIHCHsZn1upaCQNJHgGcAdwL1K1sAqzoIlntDGSQ3lQncYWxmPa/VGsFO4JKIiCwL0ysqs53Fy68R5CTWD/teAjPrfa3+zXs3SQfxQGhH0xCkN5W5acjMelyrNYJtwL2SvgbM1DdGxBWZlKrL2hUEG4fzHJhYtX3qZrZKtBoE78myEL2mEvU+ghXWCIZznDxaoxZBbgVDUc3MstTq8NHbJZ0LXBgRn5O0hmT+oFWpHTeUQRIENZJZSDcMr9rTZWZ9rtVpqN8K3AK8P910NvCpjMrUdadHDa3sr/hN6cX/mDuMzayHtfo379uBFwMnYHaRmjOyKlS3VWpBTpBfYXPOxjQIjs+4w9jMelerQTCTrjsMgKQCyX0Eq9JKp6Cu25jeVHas5CAws97VahDcLul3gNF0reJPAv+UXbG6q1wLhtrQuZvPiQ1DOY7NuGnIzHpXq0FwLTAO3AX8R5I1BpqtTNb3KitYpnKujcUcx10jMLMe1uqooRrwV+nXqteupiFIOoy/e9L3EphZ72p1rqHvMk+fQERc0PYS9YB2BsHG4TynyjNUarHiUUhmZllYylxDdSPA64At7S9Obyi38aK9qVifjrrK1pGlTPZqZtYZLbWER8Thhq+DEfE/SBa0X5UqtZXfTFY3ey+BO4zNrEe12jR0acPTHEkNYdX+eVuOYCjXniTYVEzvJXCHsZn1qFYv5n/S8LgCPAS8vu2l6RHtbBpaWxAF+e5iM+tdrY4a+omsC9JLKm3sLJbExmKeo7672Mx6VKtNQ+9caH9EvLc9xekN7Rw1BLDZQWBmPazVhvCdwH8imWzubOBtwKXA+vRrXpIul/SApH2Srp1n/9sk3SXpTkn/T9IlS/8ntFdEUG7jDWUAW4p5js1UGZAF3sysz7TaR7AduDQiTgJIeg/w6Yj45WYvkJQHbgReCRwA9kjaFRH3Nhz2sYh4X3r8FcB7gcuX/K9oo2p6rW7HFBN1W4p5KgEnyrXZiejMzHpFq3/3Pg0oNTwvpdsWchmwLyL2pxPW3Qxc2XhARJxoeLqWHpjIrl2rkzXanN5L4OYhM+tFrdYIPgx8TdI/pM9/FvjQIq85G3i44fkB4IVzD5L0duCdwDDwk/O9kaSrgasBzjnnnBaLvDzZBEFSCzgyXeW8pg1pZmbd0eoNZX8AvAU4mn69JSL+ezsKEBE3RsQzgN+myUR2EXFTROyMiJ1jY2Pt+NimTi9K0773XD+UoyDXCMysNy3lcrcGOBERfwYckHT+IscfBHY0PN+ebmvmZpKaRledXqayfTUCSWwu5jniIDCzHtTqUpW/T/IX+7vTTUPA3y3ysj3AhZLOlzQMXAXsmvO+FzY8fQ3wYCvlyVIlg6YhgC0jeY56mgkz60Gt9hH8HPB84BsAEXFI0oKt3RFRkXQNcCvJQvcfjIh7JF0P7I2IXcA1kl4BlEmanN60zH9H27RrveK5NhfzPHisRC2CXBtHJJmZrVSrQVCKiJAUAJLWtvKiiNhNsohN47brGh7/ZqsF7ZQsOoshCYIacLxUm+08NjPrBa32EXxC0vuBTZLeCnyOVbpITWW2j6C977slvfi7w9jMes2iNQJJAj4OXAycAC4CrouI2zIuW1eUI7umIYAjM1VW5Wo+Zta3Fg2CtElod0Q8G1iVF/9GWTUNrS2I4Zw4Mu0agZn1llYbQL4h6QWZlqRHZDVqKBlCmnPTkJn1nFY7i18I/LKkh4AJQCSVhedkVbBumR01lMHAni3FPI9MVtr/xmZmK7BgEEg6JyK+D/xUh8rTdeVaEgLKYIjn5mKe+4+VqNaCvBeyN7MesVjT0KcAIuJ7wHsj4nuNX5mXrgvauSjNXJuLeQI45mUrzayHLBYEjVfEgRjs0u5FaRptGTk9csjMrFcsFgTR5PGqlWkQzN5L4KkmzKx3LNZZ/FxJJ0hqBqPpYzjdWbwh09J1QbJwfTbvPVrIMZKXRw6ZWU9ZMAgiYuDmQqjU2j90tNGWYp7DvpfAzHpIRn/79q8sm4YAto7kOTztIaRm1jscBHMkTUPZBsFEJZiuuJ/AzHqDg2COSmRfIwA47H4CM+sRDoI5yrX2zzzaaGsx6ZZ5wv0EZtYjHARzZN00tKmYIy/cYWxmPcNBMEeWdxYD5KR05JA7jM2sNzgIGtQiqEa2w0ehPnLINQIz6w0OggZZzjzaaOtInuOl2uyU12Zm3eQgaHB6mcqsawQFAvcTmFlvcBA0yGp1srm2pUNIn3A/gZn1AAdBg04FwdZinhwwPuUagZl1n4OgwWwfQcZBkM+JrSN5xl0jMLMekGkQSLpc0gOS9km6dp7975R0r6RvSfq8pHOzLM9iTtcIsv+ssdGCawRm1hMyu+RJygM3Aq8GLgHeIOmSOYf9G7AzXfv4FuCPsipPK+qdxVnXCADGRvKcKNc855CZdV2Wf/teBuyLiP0RUQJuBq5sPCAivhARk+nTO4DtGZZnUaW0RjDciSAYTaaaGPfIITPrsiyD4Gzg4YbnB9Jtzfwq8Jn5dki6WtJeSXvHx8fbWMQnK1XTIMh3IgiSkUPjU+4nMLPu6onOYkm/DOwE/ni+/RFxU0TsjIidY2NjmZWjXiModqBGsGEoRzEv1wjMrOsWW6pyJQ4COxqeb0+3PYmkVwC/C7w0ImYyLM+i6kEw1IEagSTGRvI87hqBmXVZljWCPcCFks6XNAxcBexqPEDS84H3A1dExOMZlqUlpWqQF+SVfRAAnLmmwGOTFWrhqSbMrHsyC4KIqADXALcC9wGfiIh7JF0v6Yr0sD8G1gGflHSnpF1N3q4jSrXoSP9A3ZlrClTCaxOYWXdl2TREROwGds/Zdl3D41dk+flLVapGR0YM1Z21Jjn9j0xWOGM00x+FmVlTPdFZ3CtKtc4GwZZinuGceHTS/QRm1j0OggalamebhiRx5pqCg8DMuspB0KDTNQJImocen6pQ9doEZtYlDoIGne4shqTDuBrwuCegM7MucRA0KHe4sxjg7LVJJ/HDpxwEZtYdDoIGM12oEWwYzrNpOMf3T5Y7+rlmZnUOglREdHz4aN2564d4eKLsG8vMrCscBKlqQNCZmUfnOmfdEDPV4DFPN2FmXeAgSHVy5tG5zl0/DODmITPrCgdBqpNrEcy1bijHlmKe7zkIzKwLHASpTs48Op8LNgzxvVNlZqpesczMOstBkKo3DXViLYL5XLSpSDVg3/FSVz7fzAaXgyA12zTUpRrB9rUF1g3luP+Yg8DMOstBkKrXCIa6VCOQxEWbhtl/ouTmITPrKAdBqpudxXUXp81D33atwMw6yEGQmu0j6FLTECTNQ1tH8uwdnyJ8c5mZdYiDINULNQJJ7Bwb4bGpKgcmfHOZmXWGgyBVqgU5Qb6LQQDwQ1tGGMmLPY9PdbUcZjY4HASpbs0zNNdQTly6bYRvHy95wRoz6wgHQaobaxE0c9nTRhktiH85OOG+AjPLnIMg1Ss1AoCRfI4Xn7mG758qs/+Ep50ws2w5CFLdWKZyIc/fOsLmYo4vHprw9NRmlikHQarTC9cvJp8TLz1rLePTVe46MtPt4pjZKpZpEEi6XNIDkvZJunae/T8u6RuSKpJem2VZFlOqRVfvIZjPRZuGefqaAv/6yCRlL25vZhnJLAgk5YEbgVcDlwBvkHTJnMO+D7wZ+FhW5WjVZKXGaL63KkiS+Imz13KqXPNwUjPLTJZXvsuAfRGxPyJKwM3AlY0HRMRDEfEtoKuT60QEU5VgTaG3agQAO9YNceHGYe54bIqJsucgMrP2yzIIzgYebnh+IN22ZJKulrRX0t7x8fG2FK7RTDUIYKTQWzWCupc9fQ3lWvDlRye7XRQzW4V688o3R0TcFBE7I2Ln2NhY299/Kp1nqBdrBABbRwo8b9sIdz4xzZHpareLY2arTJZBcBDY0fB8e7qt50xWkiaXXusjaPTiM9eQz8Htj0x0uyhmtspkeeXbA1wo6XxJw8BVwK4MP2/Zpiq9XSOAZF3jF56xhgeOlXhk0jeZmVn7ZBYEEVEBrgFuBe4DPhER90i6XtIVAJJeIOkA8Drg/ZLuyao8C5mtEfRoH0HdC84YYTQvvnTIfQVm1j6FLN88InYDu+dsu67h8R6SJqOumpoNgt6tEQAU8zle9LRRvnBokodPldmxbqjbRTKzVaC3/wTukKlqMgV1L00x0cylY6OsLYjbD3lCOjNrDwcBSY1gTT6H1PtBMJQTP3rmGg5MVHjopPsKzGzlHATAZCV6vlmo0XO3jrBhKMftj0y6VmBmK+YgIKkR9HpHcaNCTvzYWWt4dLLCvUc9IZ2ZrUz/XP0yNNVnNQKAZ28pcuZogS8emqRUda3AzJbPQQBMVmus6aMaASQT0r18+1pOlmt85TEPJzWz5euvq18GIoLpSjDaY1NQt2LHuiGetbnIVx+b4vEpr29sZssz8EEwnU441099BI1esX0tIwWx+/unqLrj2MyWoT+vfm3UD9NLLGS0kONV29fx6GSFf/Udx2a2DAMfBP0yvcRCLt5c5HlbR7jj8SkePO5RRGa2NP179WuTqWp/TC+xmFdsX8uZowX+8bsneehEqdvFMbM+MvBBcKKUBMH6oXyXS7IyhZx4/Q9sYHMxzy37T7Dn8SnfbGZmLRn4IDg8XWU4J9b2eY0AYE0hxxt+YCPnrB/i8wcn+JsHjnHv0RlqDgQzW8DAB8GRmSpbivm+mGeoFWuGcrzugg38zLnrqNRg10Mnueneo9x1eNo1BDObV6bTUPeDI9NVtq+y6Zwl8awtI1yyuci3j5f4ymNTfPr7p7jryAyvOXcdG4f7uxnMzNproGsE5VpwolxjS3F1XhglcdGmIm965kYu35EMMf2b+4/xnePuTDaz0wY6CI7OJAvBbx1ZnUFQJ4nnbRvhLRdvYsNwjk/uP8Hthybcd2BmwIAHwZHpJAhWa41grs3FPP/+mZt47tYiX3lsipv3neBUudbtYplZlw10EBxOawSbByQIIFnY5tXnrOc156zj0ESZv77vKN98Ytq1A7MBNtCdxUemq6wfyjHchxPOrdSzt45w1poC//fhU3zm4VPc8fgkLxgb5aJNRdYODfTfB2YDZ7CDIB06Oqi2jRZ444UbeeBYia88NslnD0xw24EJtq8r8MyNRS7YMLSqhtaa2fwGNggmyjUenazwwqeNdrsoXSWJizcXuWjTMOPTVR44NsO3j5X4/MEJPn8QNgzlOH/DEBdsGObc9UOM5F1bMFttBjYI7j4yTZCs9GVJIJwxWuCM0QIvOWstx2aqfPdkie+eKHP/0RLfPDyDgKeNFhgtiJygFsnXUD65M3ttIceG4TxbRvJsLeZZU5BrE2Z9YCCDICK468gMT19TYOvIQJ6CRW0q5nl+cZTnbxulGsGhiQrfPVHi0GRldg2HHCDB5EyNRyZqTFSe3OFczIutxSQYthTzbE0DYnMxTz7ngDDrFZleBSVdDvwZkAc+EBF/OGd/Efgw8MPAYeAXI+KhLMsE8PBEhSemq/zUjrVZf9SqkJfYsW6IHYvcgV2L4ESpxpGZKoenq7PfHzpZ5u4jp6fHFrCpmGP9UJ7RglhTyLGmIEYLueRxPnk8UhDFvCjmXLMwy1JmQSApD9wIvBI4AOyRtCsi7m047FeBoxHxA5KuAm4AfjGrMk1Wauw/UeKzD0+wbijHD252s1A75SQ2FfNsKua5YMOT981Uk4A4Mp2Ew+GZKhPlGk9M1ZislJmqLjx8tZhPQmFk9nuO4ZwIoBpBNZIgqtaS57UgqbUo+cpL6WORV1KbKeTEUE4M55Q+huG8KCjZXj9e6ftIkEPJd9VrRKf319+vkEuG6ebnCa/6fE+N/9pI//OUbbOvqW+Lp7xmKe8VBBFQDajWghqna3VK/12afd7w752zrfHYXPqd9FxYf8qyRnAZsC8i9gNIuhm4EmgMgiuB96SPbwH+UpIig9nRvvLoJLc/kqzgdeZogZ+/YL07PjuomM9x1pocZ62Zv1ZRS9eOnqzUmKwGU5Ua09VgphpMV2vMzD4OZqo1js1UKdUCAflccnHP1y/ySi7qIrno1QjKtXpY1KhFEhaVWjLNSH1fu4knX5BXO/HUIBEOh3Z6+fa1PHfrSNvfN8sgOBt4uOH5AeCFzY6JiIqk48BW4InGgyRdDVydPj0l6YGVFu4tzXdtm/v5PaRXy9ar5QKXbblctuXp5bKd22xHX/SURsRNwE2d+CxJeyNiZyc+a6l6tWy9Wi5w2ZbLZVueXi7bQrJsGzkI7Gh4vj3dNu8xkgrARpJOYzMz65Asg2APcKGk8yUNA1cBu+Ycswt4U/r4tcC/ZNE/YGZmzWXWNJS2+V8D3EoyfPSDEXGPpOuBvRGxC/hr4COS9gFHSMKi2zrSBLVMvVq2Xi0XuGzL5bItTy+XrSn5D3Azs8Hm8ZNmZgPOQWBmNuAGMggkXS7pAUn7JF07z/6ipI+n+78q6bwOlWuHpC9IulfSPZJ+c55jXibpuKQ706/rOlG29LMfknRX+rl759kvSX+enrdvSbq0Q+W6qOF83CnphKR3zDmmY+dN0gclPS7p7oZtWyTdJunB9PvmJq99U3rMg5LeNN8xGZTtjyXdn/7M/kHSpiavXfDnn1HZ3iPpYMPP7aebvHbB3+mMyvbxhnI9JOnOJq/N9Ly1RUQM1BdJx/V3gAuAYeCbwCVzjvl14H3p46uAj3eobGcBl6aP1wPfnqdsLwP+uUvn7iFg2wL7fxr4DMmNpS8Cvtqln++jwLndOm/AjwOXAnc3bPsj4Nr08bXADfO8bguwP/2+OX28uQNlexVQSB/fMF/ZWvn5Z1S29wDvauFnvuDvdBZlm7P/T4DrunHe2vE1iDWC2akvIqIE1Ke+aHQl8KH08S3Ay9WBiVQi4pGI+Eb6+CRwH8nd1/3iSuDDkbgD2CTprA6X4eXAdyLiex3+3FkR8SWSUXCNGv+f+hDws/O89KeA2yLiSEQcBW4DLs+6bBHx2YiopE/vILnnp+OanLdWtPI7nVnZ0mvD64H/3c7P7KRBDIL5pr6Ye7F90tQXQH3qi45Jm6OeD3x1nt0/Iumbkj4j6VkdLFYAn5X09XTaj7laObdZu4rmv5DdOm8AT4uIR9LHjwJPm+eYXjh/v0JSq5vPYj//rFyTNlt9sEmTWrfP20uAxyLiwSb7u3XeWjaIQdDzJK0D/g/wjog4MWf3N0iaPZ4L/AXwqQ4W7cci4lLg1cDbJf14Bz97UemNi1cAn5xndzfP25NE0l7Qc+O2Jf0uUAE+2uSQbvz8/xfwDOB5wCMkTTC95g0sXBvo6d8bGMwg6OmpLyQNkYTARyPi7+fuj4gTEXEqfbwbGJK0rRNli4iD6ffHgX8gqZI3auXcZunVwDci4rG5O7p53lKP1ZvJ0u+Pz3NM186fpDcD/w54YxpUT9HCz7/tIuKxiKhGRA34qyaf2c3zVgB+Hvh4s2O6cd6WahCDoGenvkjbGv8auC8i3tvkmDPr/RWSLiP5GWYeUpLWSlpff0zSwXj3nMN2Af8hHT30IuB4Q3NIJzT9y6xb561B4/9TbwL+cZ5jbgVeJWlz2gTyqnRbppQsIPVfgSsiYrLJMa38/LMoW2Mf0881+cxWfqez8grg/og4MN/Obp23Jet2b3U3vkhGt3ybZKTB76bbrif5RQAYIWle2Ad8DbigQ+X6MZImg28Bd6ZfPw28DXhbesw1wD0kIyPuAH60Q2W7IP3Mb6afXz9vjWUTyWJE3wHuAnZ28Ge6luTCvrFhW1fOG0kYPQKUSdqrf5Wkj+nzwIPA54At6bE7SVbvq7/2V9L/7/YBb+lQ2faRtLHX/5+rj5h7OrB7oZ9/B8r2kfT/pW+RXNzPmlu29PlTfqezLlu6/W/r/481HNvR89aOL08xYWY24AaxacjMzBo4CMzMBpyDwMxswDkIzMwGnIPAzGzAOQhs1ZJUTWd8vCedWuK3JOXSfTsl/fkCrz1P0i8tsP/pkm5JH79Z0l8usWxvlvT0hucfkHTJUt7DrF0yW6rSrAdMRcTzACSdAXwM2AD8fkTsBRaaEvg84JfS1zyJpEJEHCK52XC53kxyY9EhgIj4tRW8l9mKuEZgAyGS2/uvJpnATErWJ/hnAEkvbZhX/t/SO0H/EHhJuu0/p3/B75L0L8Dn0xpD4x2iOyR9Uck6Ar+fvu+TjpH0LiXz67+W5Eayj6bvP5q+dmd63BvS+evvlnRDw+tPSfqDtHZzh6T5Jq4zWzIHgQ2MiNhPMnf9GXN2vQt4e1p7eAkwRbJmwL9GxPMi4k/T4y4FXhsRL53n7S8DfgF4DvC6+kW9STluIamNvDF9/6n6vrS56AbgJ0kmWnuBpJ9Nd68F7ohk4rwvAW9t8Z9utiAHgRl8GXivpN8ANsXpufnnui0ims2Xf1tEHE4v6n9PMl3IcrwA+GJEjKfl+CjJoigAJeCf08dfJ2m+MlsxB4ENDEkXAFXmzPwZEX8I/BowCnxZ0sVN3mJigbefO1dLkEzp3Pg7NrKkAj9VOU7PCVPFfXzWJg4CGwiSxoD3AX8ZcybYkvSMiLgrIm4gmcnyYuAkyXKhrXqlknWJR0lWH/sy8BhwhqStkook0zzXNXv/rwEvlbRNUp5kRtXbl1AOsyXzXxS2mo0qWVB8iOSv848A803v/Q5JPwHUSGaI/Ez6uCrpmyQzTB5d5LO+RrKOxHbg79JRSUi6Pt13ELi/4fi/Bd4naQr4kfrGiHhEyeLrXyCZzfXTETHflNVmbePZR83MBpybhszMBpyDwMxswDkIzMwGnIPAzGzAOQjMzAacg8DMbMA5CMzMBtz/B2t+EE6CpZ4FAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "rv = sp.stats.f(5, 10)\n",
    "\n",
    "rvs = rv.rvs(size=10000)\n",
    "ax = sns.distplot(rvs, bins=100, kde=True, hist=False,\n",
    "                  color='skyblue', hist_kws={\"linewidth\": 15,'alpha':1})\n",
    "ax.set(xlabel='Distribution', ylabel='Frequency')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.8.9"
  },
  "nikola": {
   "category": "",
   "date": "2019-02-24",
   "description": "",
   "link": "",
   "slug": "ml-descriptive-statistics",
   "tags": "",
   "title": "Machine Learning - Descriptive Statistics",
   "type": "text"
  },
  "toc": {
   "base_numbering": 1,
   "nav_menu": {},
   "number_sections": true,
   "sideBar": true,
   "skip_h1_title": false,
   "title_cell": "Table of Contents",
   "title_sidebar": "Contents",
   "toc_cell": false,
   "toc_position": {},
   "toc_section_display": true,
   "toc_window_display": false
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}