{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Anomaly Detection \n"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
""
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"python ver=3.8.9 (default, Jun 12 2021, 23:47:44) \n",
"[Clang 12.0.5 (clang-1205.0.22.9)]\n",
"pandas ver=1.2.4\n",
"numpy ver=1.23.1\n",
"scipy ver=1.9.0\n"
]
}
],
"source": [
"# 경고 메시지 출력 끄기\n",
"import warnings \n",
"warnings.filterwarnings(action='ignore')\n",
"\n",
"# 노트북 셀 표시를 브라우저 전체 폭 사용하기\n",
"from IPython.core.display import display, HTML\n",
"display(HTML(\"\"))\n",
"from IPython.display import clear_output\n",
"\n",
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"\n",
"import os, sys, shutil, functools\n",
"import collections, pathlib, re, string\n",
"\n",
"rseed = 22\n",
"import random\n",
"random.seed(rseed)\n",
"\n",
"import numpy as np\n",
"np.random.seed(rseed)\n",
"np.set_printoptions(precision=5)\n",
"np.set_printoptions(formatter={'float_kind': \"{:.5f}\".format})\n",
"\n",
"import pandas as pd\n",
"pd.set_option('display.max_rows', None) \n",
"pd.set_option('display.max_columns', None) \n",
"pd.set_option('display.max_colwidth', None)\n",
"pd.options.display.float_format = '{:,.5f}'.format\n",
"\n",
"import scipy as sp\n",
"\n",
"import seaborn as sns\n",
"\n",
"from pydataset import data\n",
"\n",
"print(f\"python ver={sys.version}\")\n",
"print(f\"pandas ver={pd.__version__}\")\n",
"print(f\"numpy ver={np.__version__}\")\n",
"print(f\"scipy ver={sp.__version__}\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"## Outlier\n",
"\n",
"통계적 의미에서 이상치는 데이터의 분포에서 상당히 벗어난 값을 의미 합니다. 이 값은 비정상 적인 값일 수도 있지만, 새로운 관측치일 수도 있습니다. 이 부분에 대한 판단은 자신이 분석하고 있는 데이터의 도메인 특성에 상당히 종속됩니다. \n",
"\n",
"따라서, 이상치는 데이터를 모델링 하는데 있어 주로 하는 가정이 해당 데이터는 특정 분포를 따른다는 가정이기 때문에, 이상치를 포함한 데이터를 통한 모델링은 이상치에 강건한 모델링 방법이 아니라면 안좋은 영향을 주게 될수도 있지만, 다른 도메인에서 이상치는 가정한 정상 분포를 벗어나는 새로운 데이터이기 때문에 제거해야 할 대상이 아닌 탐지해야 할 대상이 될 수 도 있습니다. 빅데이터로 인해 대표본의 시대가 되면서 이상치의 인위적인 제거 보다는 이상치 또한 하나의 데이터 특성으로 간주하고 모델링 하는 경향이 증가하고 있습니다. 이는 어느정도 모델의 강건함을 증가시키는데 도움이 될 수도 있습니다.\n",
"\n",
"자신이 풀고자하는 문제 정의에 맞게 데이터에서 이상치를 허용할지, 제거할지, 다른 값으로 채워 넣을지, 아니면 탐지하여 알람을 보낼지 선택하면 됩니다.\n",
"\n",
"이상치를 탐지하는 방법은 크게 이상치가 단변량(Univariate)이냐, 다변량(Multivariate)이냐에 따라 방법이 달라지게 됩니다.\n",
"\n",
"* 단변량 이상탐지는 값들이 1차원 상에 분포하기 때문에 주로 분포를 가정한 통계적 방법이 사용됩니다.\n",
" * Z-score\n",
" * Tukey Outlier\n",
"* 다변량 이상탐지는 2차원 이상에 분포하기 때문에 주로 벡터 거리 기반 또는 트리 방법을 통한 클러스터링 방법이 주로 사용됩니다.\n",
" * DBScan Clustering\n",
" * Isolation Forest\n",
" * Robust Random Cut Forest"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Univariate \n",
"\n",
"통계적 방법에 의해 이상치를 제거하는 단변량 방법에 대해서 살펴보도록 하겠습니다."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
".. _boston_dataset:\n",
"\n",
"Boston house prices dataset\n",
"---------------------------\n",
"\n",
"**Data Set Characteristics:** \n",
"\n",
" :Number of Instances: 506 \n",
"\n",
" :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.\n",
"\n",
" :Attribute Information (in order):\n",
" - CRIM per capita crime rate by town\n",
" - ZN proportion of residential land zoned for lots over 25,000 sq.ft.\n",
" - INDUS proportion of non-retail business acres per town\n",
" - CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)\n",
" - NOX nitric oxides concentration (parts per 10 million)\n",
" - RM average number of rooms per dwelling\n",
" - AGE proportion of owner-occupied units built prior to 1940\n",
" - DIS weighted distances to five Boston employment centres\n",
" - RAD index of accessibility to radial highways\n",
" - TAX full-value property-tax rate per $10,000\n",
" - PTRATIO pupil-teacher ratio by town\n",
" - B 1000(Bk - 0.63)^2 where Bk is the proportion of black people by town\n",
" - LSTAT % lower status of the population\n",
" - MEDV Median value of owner-occupied homes in $1000's\n",
"\n",
" :Missing Attribute Values: None\n",
"\n",
" :Creator: Harrison, D. and Rubinfeld, D.L.\n",
"\n",
"This is a copy of UCI ML housing dataset.\n",
"https://archive.ics.uci.edu/ml/machine-learning-databases/housing/\n",
"\n",
"\n",
"This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.\n",
"\n",
"The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic\n",
"prices and the demand for clean air', J. Environ. Economics & Management,\n",
"vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics\n",
"...', Wiley, 1980. N.B. Various transformations are used in the table on\n",
"pages 244-261 of the latter.\n",
"\n",
"The Boston house-price data has been used in many machine learning papers that address regression\n",
"problems. \n",
" \n",
".. topic:: References\n",
"\n",
" - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.\n",
" - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.\n",
"\n",
"['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'\n",
" 'B' 'LSTAT'] MEDV\n"
]
},
{
"data": {
"text/html": [
"\n",
"\n",
"
\n",
" \n",
" \n",
" CRIM \n",
" ZN \n",
" INDUS \n",
" CHAS \n",
" NOX \n",
" RM \n",
" AGE \n",
" DIS \n",
" RAD \n",
" TAX \n",
" PTRATIO \n",
" B \n",
" LSTAT \n",
" \n",
" \n",
" \n",
" \n",
" 0 \n",
" 0.00632 \n",
" 18.00000 \n",
" 2.31000 \n",
" 0.00000 \n",
" 0.53800 \n",
" 6.57500 \n",
" 65.20000 \n",
" 4.09000 \n",
" 1.00000 \n",
" 296.00000 \n",
" 15.30000 \n",
" 396.90000 \n",
" 4.98000 \n",
" \n",
" \n",
" 1 \n",
" 0.02731 \n",
" 0.00000 \n",
" 7.07000 \n",
" 0.00000 \n",
" 0.46900 \n",
" 6.42100 \n",
" 78.90000 \n",
" 4.96710 \n",
" 2.00000 \n",
" 242.00000 \n",
" 17.80000 \n",
" 396.90000 \n",
" 9.14000 \n",
" \n",
" \n",
" 2 \n",
" 0.02729 \n",
" 0.00000 \n",
" 7.07000 \n",
" 0.00000 \n",
" 0.46900 \n",
" 7.18500 \n",
" 61.10000 \n",
" 4.96710 \n",
" 2.00000 \n",
" 242.00000 \n",
" 17.80000 \n",
" 392.83000 \n",
" 4.03000 \n",
" \n",
" \n",
" 3 \n",
" 0.03237 \n",
" 0.00000 \n",
" 2.18000 \n",
" 0.00000 \n",
" 0.45800 \n",
" 6.99800 \n",
" 45.80000 \n",
" 6.06220 \n",
" 3.00000 \n",
" 222.00000 \n",
" 18.70000 \n",
" 394.63000 \n",
" 2.94000 \n",
" \n",
" \n",
" 4 \n",
" 0.06905 \n",
" 0.00000 \n",
" 2.18000 \n",
" 0.00000 \n",
" 0.45800 \n",
" 7.14700 \n",
" 54.20000 \n",
" 6.06220 \n",
" 3.00000 \n",
" 222.00000 \n",
" 18.70000 \n",
" 396.90000 \n",
" 5.33000 \n",
" \n",
" \n",
"
\n",
"
"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAFvCAYAAABq/iEqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAnj0lEQVR4nO3dd3yV5f3/8dcnezEChBn2RkCBOBGrgttWpFato67Wfr/tr2ptraP2+61ddjk6tK2jiv1axYGzbhQHKBCUvUEgYYaVkED29fvjHELGSU6AnJxzhffz8ciD3Ne57/t8jsQ3V677vq/LnHOIiIg/4qJdgIiIHBoFt4iIZxTcIiKeUXCLiHhGwS0i4pmEaBfQHOeee6576623ol2GiEhrs1CNXvS4d+zYEe0SRERihhfBLSIiBym4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ848VcJSLigYr9sPodiEuAQWdBQlK0K2qzFNwicuT274HHJsHO1YHt7qPhhncgMTWqZbVVGioRkSO38NmDoQ2wdREsezV69bRxCm4ROXLlxSHa9rZ+HUcJBbeIHLlR34Dk9ge307rAiMlRK6et0xi3iBy5zL5w40z4/CmIT4Sx10B6l2hX1WYpuEWkZXQeCGfdE+0qjgoaKhER8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMxENbjP7oZktNbMlZvaMmaWYWX8zm2Nma8xsmpklRbIGEZG2JmLBbWa9gJuAHOfcSCAeuBz4HfCAc24QsBu4IVI1iIi0RZEeKkkAUs0sAUgDtgBnAi8EX58KTI5wDSIibUrEgts5twn4I7CRQGAXAvOBPc65yuBu+UCvSNUgItIWRXKoJBO4COgP9ATSgXMP4fgbzSzXzHILCgoiVKWIiH8iOVQyCfjSOVfgnKsApgPjgY7BoROAbGBTqIOdc48453KcczlZWVkRLFNExC+RDO6NwElmlmZmBkwElgEfAJcE97kGeCWCNYiItDmRHOOeQ+Ai5OfA4uB7PQLcDtxqZmuAzsDjkapBRKQtMudctGsIKycnx+Xm5ka7DBGR1mahGvXkpIiIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxLC7yIiEkELp8GqN6HLEDj5+5DSIdoVxTwFt4hEz5xH4M3bDm5vmA3Xvh69ejyhoRIRiZ4FT9fdXv8x7MmLTi0eUXCLSPSk11tPNj4ZUtpHpxaPKLhFJHrOuKvWmLbBGXdqjLsZNMYtItHTayzcsgQ2fgZdBkGnAdGuyAsKbhGJrpT2MOTsaFfhFQ2ViIh4RsEtIuIZBbeIiGcU3CIinlFwi4h4RsEtIuIZBbeIiGcU3CIinlFwi4h4RsEtIuIZBbeIiGcU3CLSOqqrID8XCjdFuxLvaZIpEYm8PXnw1Ndg1zqwOPjK7XD6HdGuylvqcYtI5H38x0BoA7hq+PB3UJgf3Zo8puAWkcirPzziqqFoS3RqaQMU3CISeSOn1N3O7B9YREEOi8a4RSTyjrsi8OeSF6FDNkz4EcTFR7cmjym4RaR1HHfFwQCXI6KhEhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfFMRIPbzDqa2QtmtsLMlpvZyWbWyczeNbPVwT8zI1mDiEhbE+ke95+At5xzw4BjgeXAHcAM59xgYEZwW0REmiliwW1mHYDTgMcBnHPlzrk9wEXA1OBuU4HJkapBRKQtimSPuz9QADxhZl+Y2WNmlg50c85tCe6zFegW6mAzu9HMcs0st6CgIIJlioj4JZLBnQCMBf7mnBsDlFBvWMQ55wAX6mDn3CPOuRznXE5WVlYEyxQR8UskgzsfyHfOzQluv0AgyLeZWQ+A4J/bI1iDiEibE7Hgds5tBfLMbGiwaSKwDHgVuCbYdg3wSqRqEBFpixIifP4fAE+bWRKwDriOwD8Wz5nZDcAG4NII1yAi0qZENLidcwuAnBAvTYzk+4qItGV6clJExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltEmuYcFG6C6qpoVyJBEV3lXUQ8t3UxTLsadn8J7bPhkn9CnxOjXdVRTz1uEWnc67cGQhugKB9e/UF06xFAwS0iTdm+vO72jpUaMokBCm4RadzgSXW3B54JcfHRqUVqaIxbRBp34YOQlAEbZkOvcXDOr6NdkaDgFpGmpHaEi/4a7SqkHg2ViIh4RsEtIuIZBbeIiGcU3CIinlFwi4h4RsEtIuIZBbeIiGcU3CIinlFwi4h4psknJ81sSlOvO+emt2w5IiISTrhH3l8AFgS/AKzWaw5QcIuItLJwwT0FuBwYDbwCPOOcWxPxqkTEH+UlsOINMINhF0BiarQravOaDG7n3MvAy2aWDlwE3GdmnYGfOuc+bIX6RCSW7d8Dj54Bu9YFtrOGwbdnQHJGVMtq65p7cbIUKASKgAwgJWIViYg/Fj13MLQBClbA0peiV89RItzFyTMJDJWcALwH/Mk5l9sahYmIBypLm9cmLSpcj/s9AqH9CZAMfMvM/nzgK+LViUhsG/UNSO10cDu9KxxzcfTqOUqEuzh5PYG7R0REGmrfA777ESx4GiwOxlwF6V2iXVWbZ87Ffi7n5OS43FyN0IjIUcdCNYYb436NJnrczrmvHWFRIiJyiMINlfyxVaoQEZFmC3cfd6P3apvZ+JYvR0REwgk3VBIPXAr0At5yzi0xswuBu4BUYEzkSxQRkdrCDZU8DvQG5gJ/NrPNQA5wR/CpShERaWXhgjsHGO2cqzazFGArMNA5tzPypYmISCjhHsApd85VAzjnSoF1Cm0RkegK1+MeZmaLgt8bMLDWNs650RGrTESOLnlzYdkr0LFv4EGepLRoVxSzwgX3sUA3IK9ee28CwyYiIkdu1dvwzOUQ+AUflr8K174e3ZpiWLihkgeAQufchtpfBGYKfCDy5YnIUWHeYwdDG2D9x7B9efTqiXHhgrubc25x/cZgW7+IVCQiR59Qiy8kaPboxoQL7o5NvKZlLkSkZYy/GRLTD24fewV06h+9emJcuDHuXDP7jnPu0dqNZvZtYH5z3iD4EE8usMk5d6GZ9QeeBToHz3G1c6780EsXkTaj1zi46XNY/Q507AP9vxLtimJak7MDmlk34CWgnINBnQMkARc758JeoDSzW4PHtA8G93PAdOfcs2b2d2Chc+5vTZ1DswOKyFEq5OyATQ6VOOe2OedOAe4B1ge/7nHOndzM0M4GLgAeC24bcCaB1eMBpgKTm1W+iIgA4YdKAHDOfQB8cBjnfxD4CdAuuN0Z2OOcqwxu5xOYB6UBM7sRuBGgT58+h/HWIiJtU3MXCz5kwcmotjvnmjUWXp9z7hHnXI5zLicrK6uFqxMR8VezetyHaTzwNTM7n8Cq8O2BPwEdzSwh2OvOBjZFsAYRiVWF+YH1KvWE5CGLWI/bOXency7bOdePwErx7zvnriQw5HJJcLdrgFciVYOIxKDi7fDomfDAMXDfUPji6WhX5J2IBXcTbgduNbM1BMa8H49CDSISLTPvhU3BEdSyIvjPrbB/d3Rr8kwkh0pqOOdmAjOD368DTmiN9xWRGJKfCzPugbx5ddsrS2H3ekjNjEpZPmqV4BaRo1xZMfzfFCgtbPha+2zoNqr1a/JYNIZKRORokz+vYWgntYMh58FVL0C8+pCHQv+1RCTysoaCxYOrOth24ndh4s+iV5PH1OMWkchr3xPO/0Oglw0w8MzAxFJyWNTjFpHWcfwNcNwVUF4C6V2iXY3XFNwi0noSU0PPvS2HREMlIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwR3DKquqmb12B8u3FEW7FBGJIQnRLkBCK9hbxmX/+JR1O0oAmDKmF/dfdlx0ixKRmKAed4x6cvaXNaENMP2LTSzI2xO9gkQkZii4Y1TB3rJmtYnI0UfBHaMmj+mF2cHtru2SOXVQl+gVJCIxQ2PcMeqUgV146voTeD43n8y0RL49YQCpSfHRLktEYoCCO4ZNGJzFhMFZ0S5DRGKMhkpERDyj4BYR8YyCO4ZVVzs+WlXAfxZtYV95ZbTLEZEYoTHuGFVd7bjmibl8vHoHAD06pPDS98bTvUNKlCsTkWhTjztGfbpuZ01oA2wpLOVfn62PXkEiEjPU445Re0sbDo0Uh2hrSZVV1cxYsZ2CvWWcPaIbXdurdy8SixTcMer0oVlkZ6aSv3s/AEnxcXwjp3ezjt1SuJ+pszdQVFrBpTm9Oa53x2Ydd/3UXD5aVQDA795cwYvfO4Uh3dodVv0iEjkK7hiVkhjP9O+dwtOfbaSotIJLxmVzTM8O7CwuY1F+Icf0ak/Xdg17xPvKK5ny8Gy2FJYC8HxuHi/+9ymMzu7Y5PstyNtTE9oAe8sqeWLWl9w7ZXSLfi4ROXIK7hjWtV0KPzxrSM32jOXb+N7Tn1NWWU1ivPHAZcdx4eiedY75cGVBTWgDVFQ5XpyfHza4yyurG7SVhWgTkejTxUmP/PqN5TVhWlHl+NXryxvs0yE1sVlt9eX0zWR0doea7aT4OK4+qe8RVCsikaIet0d21JsdcFdJOc45rNZsVCcP7MzpQ7KYGRz2SE2M59TB4SeniosznvnOSbz4eT4Fe8v46rE9Nb4tEqPU4/bIlLHZdbYnj+lZJ7QBzIycfpk12/srqvjhtIVUVbuw509PTuBbJ/fjR2cPVWiLxDD1uD1y9wXD6dMpjblf7uK4Ph25fnz/kPt9sLKgzvamPftZuXUvI3q2b40yRSTCFNweSYiP4/pT+3P9qaED+4DBXTOYv2F3zXZqYjyllVVMm7eRcX07MahrRqRLFZEIUnC3QbeeNYTlW4pYmF9Iu5QEzjmmO1Meng2AGfzhkmO5ZFx2mLOISKzSGHcbtHRzESN7deCWSYP55CdnMHPl9prXnIMH3l0VxepE5Eipx93GPDcvj5+8uKhme8mmIkrKqurso5kGRfymHncb8/ScDXW231u+jSlje9Vp0/3ZIn5Tj7uNSU+u+1eaGG/cds5Qju/XiS827ianXye+emzPRo4WER8ouNuYmyYOZv6G3TVPWN542gA6piUxeUwvJo8J9Lx3l5STt3sfw3u0JzFev3SJ+EbB3cacNKAzH//kDD5Zs4NBXTMazFEybd5GfvbKUsorq+nZIYWp15/AYD1sI+KViHW3zKy3mX1gZsvMbKmZ3Rxs72Rm75rZ6uCfmeHOJQFbC0sp3F8Rdr+u7VOYMja7QWjvK6/kF68tq5lQanNhKb9/e2UkShWRCIrk78mVwI+ccyOAk4Dvm9kI4A5ghnNuMDAjuC1N2F9exXVPzOWke2dw/K/e4/7DvJ1vV0k5JeV17zDJ27WvJUoUkVYUseB2zm1xzn0e/H4vsBzoBVwETA3uNhWYHKka2op/fba+5jH28qpq/jxjNcu3FIXcd+XWvdz7xnL++v5qdhbXnZQqOzONY2vNAAhwwagekSlaRCKmVca4zawfMAaYA3Rzzm0JvrQV6NYaNfhszfbikG3De9Sde2TZ5iIufnhWzYXJ53LzeeeHp5GSGF+zz6PX5PDnGatZs72YicO6cUOYx+dFJPZEPLjNLAN4EbjFOVdUezY755wzs5DT1pnZjcCNAH369Il0mTFt4vBuPJebX7OdmhjPKQM7N9jvudy8OosfbNy1jw9XFXDOMd1r2rq2S+FXk0dFtmARiaiI3gtmZokEQvtp59z0YPM2M+sRfL0HsD3Usc65R5xzOc65nKysrEiWGfPOOaY7v7l4FKOzOzBhcBeeuuEEOmckN9gvLSm+WW1NeS43j/G/fZ+cX73LX99ffdg1i0jkRKzHbYGu9ePAcufc/bVeehW4Bvht8M9XIlVDW3LFiX244sSmf/O46qS+vDA/n+3BBRdOGtCJ8QPDL6JwwLLNhfzkhYOPy//xnVUM6daOs2v12EUk+iI5VDIeuBpYbGYLgm13EQjs58zsBmADcGkEaziq9OyYyowffYUZy7fTPjWBrwzpSlychT8w6G8frm3Q9vScjQpukRgTseB2zn0CNJYaEyP1vke7dimJbC0q5eGZ+Tz28Zf8+JyhjO3TvFvld5c0vEf8w1UFPDHrS65rZNEGEWl9et65jXluXh6/fXMFq7YVM3vtTq7551z2loZ/aAdgQiNrUz716YaQ7SISHQruNuaDlXWv9e4trayzGk5Trh3fj6+FmIAqNfHQLnCKSGQpuNuY+ov8xhnNXqrMOThvZHcuGH1wTDs+zrhp4uAWrVFEjowmmWpjvj2hP1/k7eGjVQWkJcVz2zlDyc5MC3tccVklFz80i9XBh316Z6Zyw6n9OX1oV/p1SY902SJyCBTcbUy7lESeuv4ECvaWkZ4cT1pS8/6KX12wuSa0AfJ27yc5MV6hLRKDNFTSRmW1Sw4Z2ht37uPTtTtrZgg8INRyZp9v2M22otKI1Sgih8ecC/nEeUzJyclxubm50S7De/e/s5K/fLAG56BnhxT+/Z2TKCqtYEthKUO7ZTD54dns2Vf3DpSEOOOBy47Tqjki0RHylmoNlbRhRaUVvL98O5npSQzOyuCvwdCGwFzc1z85j3U7SgDonJ7EQ98cy6frdvLUp+spKg30wCurHfe+sVzBLRJDFNyeqKyq5vVFW1hXUMykEd0aLJJQ38ad+5jyt1nsKC4HYFzfjlTX++XqQGgD7Cwp55WFm/j9Jcfy5Oz1dfbbWVLeEh9BRFqIxrg9cfO0BdwybQF/fn8Nkx+axTtLtza5/5Oz19eENsD8DXvIzkxt8pjdwWGSS8Zl12n/Rk52qN1FJEoU3DHuy4JifvnaUv6zaEtNW7WDxz/5ssnjQl1svO2coXROT2r0mEtzegNw9wXD+dHZQxjavR0Th3Xl+6cPOszqRSQSNFQSw37+6tIGwxYHNLY6+77ySu55dRlvLNmCAQdGRwZkpXP+qB4szCvkn7Pqhn68wY/PGcZZIwJrWuwqKeeJWevZVVLOyq17WfzQLN6+5TQymwh9EWk96nHHqJVb9zYR2saNpw0I+dp976xiWm4ee0srcUBKQhx9OqVRUVXNg++t4uaJg/j62F51jqly8OL8vJrtlxdsYletce3te8t4ffEWRCQ2qMcdo7Y2cv90elI8r/3gVAZkZVBZVU1ltauzNNln63bW2b+0spqNwQWBH/pgLQlxcSGnes3bvb/m+1C9+aT45k8PKyKRpR53jDqxfye6t09p0P4/Xx3BgKwMps5ez9hfvsvI/32bHz+/kIqqwAM1I3u1b3BMbY98tI7nay2DdkDtJyQvHtOL3p0OXsgckJXOBaN1O6BIrFCPO0alJMZz9ohu/N+cDVQ76Ns5jb9fNY7hPdqztqCYn7+2tOae7Bfm5zM6uwPfOrkf3z1tINPmNQzmA/ZXVDVoizP49eSRVFZVs2RzET07pvDmzafx1pKtxMcFlk5r7qPzIhJ5+r8xRi3M28NTnx2cB3vDzn3kbtjN8B7tWbq5iPoPvC7OLwRgQFYGo7M7sCi4DYEx8Yoqx8ie7VmyuajOcYO7ZvDbr48mKyOZM+6bSd6u/STEGbefO4zvNDKOLiLRpaGSGLVq294GbauDbcf3yySx3pjz+EEHF0F4+MqxnHNMN/p0SuOKE/sw566JzL97Eq/fNIFJw7vV7Nc5PYnHrslhXN9MHpyxirxdgXHuymrH799ewc7iskh8NBE5Qupxx6jxg7qQEGdU1nrc8cCETz06pPK3K8fxh3dWsmn3fjLTEllbUExpRRUpifFkZ6bxj6tzQp730W+NY9aanewsKeP0oV3pkJoIwKZaFycBKqoc24rKQq4mLyLRpeCOUT07ptKnUyrrduyraXtn6TZunbaAt5ZupUeHFLq1T2Hl1r0Ul1Xyl/fXsGZ7MX+7alyT5zUzTg2xRNmFx/Zkzpe7arYHZqUzrHu7BvuJSPQpuGPY3tK6FxIdMP2LTQCsLShhbUFJndffXLKVu15azG8uHnXI73X1SX2JM3hz8VZ6d0rlB2cOPqQV4kWk9Si4Y9iQ7hkUrDm0ceZ/z9nIxWN6cXy/Tk3u99m6nTyfm8/O4jI6pidyUv/ObC8qY0dxYAGGUHefiEhsUHDHsJ9dOIKv/WUW5cF7tDPTEmsmggJIio+j2rk64+AAebv2NRnc89bv4opHP6szW+DLX2yu+X7F1r0s21LEzB+fQbx63SIxR3eVxLBh3dvz1i0TuGniYO6+YDhTrzuBjOSD/9aeN7I7d5w7tMFxQ8OMTU//PL/BFK/15e3aH/LOFhGJPvW4Y9yArAxuPWsIAD97eQnFZQdn/Xtt0WbSUxr+FS7I28MxPTs0es5OzZgsKjUxnl5hpoEVkehQcHtk0566t+xVO0hLim+wX+96q7rv2VeOmfHU7PU8Oy+P9OT4BsMu9SUlGHPX7WLSiG6N7iMi0aHg9sgFo3rw/ortNdtpSfGcMTSL5VuKmLUmMLnU5DE9mRC83a+62nHn9MU8Pz8P5w5O8QpgYYauC/dX8p1/5TL9v09hTJ/Mlv4oInIENMbtka+Py+buC4Zz4HrhvvIqrnxsLt3ap3DXecPIapfMy19s5srH5rBiSxG3vbCQabl5VNcLbaDBI/OhOAdvL93W4p9DRI6MetyeiY+zBhcWp3++qc727LU7ueihWZRVVh/x+/XplBZ+JxFpVepxe6ZzevMeQQ8X2necO5Trx/ej9ohJl4zEOvv0aJ9CYrxRHe4WFBFpVQpuzxSXNX5B8VD0zEzj9vOGccbwrsQB8WZMHN6dT24/gynBFXK2FJVy2wuL+OV/lrXIe4pIy9BQSQxbV1DMvz7bQFW144oT+zCse3uWb2l4b3VqYhz7Kw72sAd0SWdfeVWjq+gA7NhbyphfvMu+8uATks4xbV4ery/aTGlF3d76v+ds5KfnDyehkXUuRaR1Kbhj1Pa9pUx+aBZFpYH7tp/PzefNmydwYv9O/KvWPN0APzxrCKlJCSzO38PJAzsz+bheFJVW8ovXlvJivfFvCMzP/fHqHQdDu5aSsoZtldWuWRczRaR1qAsVo95asrUmtCGwcs1rCzcza+2OBvv+5o0V7Cur5PeXHMvFY7IxMzqkJjIixEM4ifHGny4fw9qC4mbXUlXt+LTeWpYiEj0K7hh1YJ7s2nI37OaZuXkh9oZpuYH2ssoqSssreenzfMoqqsio9YBOamIc//nBBCYO78rO4vKQ52lMeQvcoSIiLUNDJTHq3JHdGdc3k/kbdgMwvHs75jTR6+2YmsRPX1rMc/PyqKh1F0hivHHBqB50zkjiyhP7MqR7Oz5YsZ2SEMMkjRmYlc5pQ7IO/8OISItScMeo5IR4nv/uyXy6bieV1Y4+nVI5+4GPQu6bkhhHTr9MHvloXYPXKqocu0rKeejKsQA8/smX3PvG8rDvH2dw/qgeZHdM5b++MpCkBP1yJhIrFNwxLC7OGD+oC6UVVZz5x5lUVNW9QnjLxEEM7d6eE/p34sH3Vjd6nh3BtSML91Xwu7dWNJgGtr52yfFcfkIfnvp0A2WV1by/cjtPXncCPTtq0imRWKBulAc+Wb2DzYV1b+2bNLwrFx7bk7TkBNKTEzh5YOdGj792fD8AdpSUNWusem9ZFU/MWl/zEM+qbcU88O6qw/8AItKi1OOOcUX7K/j92ysatC/eVMik+wNDJ3EGCfFxZGemkL/7YMBnJMdz5/nDufLEvgAMzMpgQFY66+oteRZK/V75+p3hjxGR1qHgjmGVVdWc9ocP2BNi+tVtRQeXNKt2gbs+aoc2QHFZFWcNrzsta3MeX++Ulkh6cgJ5tVZ+P+eY7odavohEiII7hj392YaQoX0o/j13A5fm9KkZn87bta/J/U8Z2JmfXTiCtKR47n93FRt37eO8kd25fnz/I6pDRFqOOQ8eicvJyXG5ubnRLqPVTbpvJmuaMawRTnycced5w/j2hAEMu/tNSsOMc6ckxHHXBcP51sn9jvi9ReSIhJw5XxcnY1iTK9TEG5cdn83o7A4kBCfoToiDnh0azh5YVe34w9sr2V1SxlUn9Q37vqWV1fzPK0u5983wtw2KSOtTcMewcX0bX3mmvMoxoEsGo3p1qLmQWFkNW2uNfddWVlnNWQ98xGOffNns9//Hh+v4fOPuQytaRCJOwR3D/uerI0hp4sGXymrXYM6Rxq49ZiQnsOMQH3MHWBFiNkIRiS4Fd4yqrnb8/NWlTY5Hv/RFPhWVdZO6e/tkju9Xt6eekhBHnB3etYz/LN7cYJFiEYkuBXeMmrV2B+8t397kPmu2lzA/OJSRkRzPWSO68a8bTuTsEXVv3SutrKZP5/TDq2PNTm5+5ovDOlZEIkPBHaN2lRzasEZxWRW/njySwd3akVprRsADLsvpTZeMpLDnyUxNICO57l2iuRt2U1zaMivviMiRU3DHqNOHdqVzevigrW3xpkIAPt9Q94Ji/y7pTBmbzbyfTuK43h2bPMfu/ZUM79GuQftfPlhzSLWISOQouGNUh9REHr5ybM2tfs3ROSOZFVuLmP5F3VVv1u8oYdTP3+aih2bxo7OHNHnBc2i3DO44b1iD9reWbG1+8SISUQruGHbbCwvDzuR3wAn9O5GdmcquEHeOOAJ3myzKL+Se15bRr0vj491FpZV0Sk8iM63uQg59D3OMXERanoI7Ru0rr2TjrubfzTH3y13k/Oo97nltGe1SGp/JYM32Yr55Qp9GX99SWMqVj83hrGO6kx4cK+/ZIYW7zm/YCxeR6NBcJTEqNTGeTmkJ7NpXGX7nWlZu20v7JoK7S0YS15zSj6Hd2/Hesm2sKyjh/ZV1717ZvKeU5+blkZ4Uz1eGZHHvlJH07Jh2WJ9DRFqegjtGmRnJCQnAoQU3UGeR4fp2FJcz4Xfvs2d/BXub2A+gpLyKD1cV8INnFvDif59yyHWISGRoqCSGbd1bGn6nw5C3e3/Y0K5t/obdrNmuJyhFYoWCO0ZtKdwfuKoYI16qd6eKiERPVILbzM41s5VmtsbM7ohGDbHu4Q/WxFJuszi/MNoliEhQqwe3mcUDDwHnASOAb5rZiNauI9a9kJsX7RLqmL1mR7RLEJGgaPS4TwDWOOfWOefKgWeBi6JQR0zbXxlL/W2IsXJEjmrRCO5eQO3uZH6wrQ4zu9HMcs0st6CgoNWKixXNf15SRI42MXtx0jn3iHMuxzmXk5WVFe1yWt1Fx/aIdgl1dElPDL+TiLSKaAT3JqB3re3sYJvU8uA3x/LtU/tFuwwAurZLZO5Pz4p2GSIS1OqLBZtZArAKmEggsOcBVzjnljZ2zNG6WLCIHPVCjpq2+pOTzrlKM/t/wNtAPPDPpkJbRETqisoj7865N4A3ovHeIiK+i9mLkyIiEpqCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8Uyrz1VyOMysANgQ7To81gXQSggSDfrZOzI7nHPn1m/0IrjlyJhZrnMuJ9p1yNFHP3uRoaESERHPKLhFRDyj4D46PBLtAuSopZ+9CNAYt4iIZ9TjFhHxjIJbRMQzCm5pkpmtN7Mu0a5D/GBm15pZz1rbM80sJ/j9G2bWMWrFtSEK7jYsuDCzSGu6FugZ6gXn3PnOuT3NPZGZxbdQTW2OgjvGmVk/M1tuZo+a2VIze8fMUs3sODP7zMwWmdlLZpYZ3H+mmT1oZrnAzcHtB8wsN3ie481supmtNrNf1Xqfl81sfvA9bozaB5aYY2a3mtmS4NctwZ/JJbVe/7GZ/dzMLgFygKfNbIGZpdY7T81vb2Z2lZnNDe73jwMhbWbFZnafmS0ETm7Fj+kVBbcfBgMPOeeOAfYAXweeAm53zo0GFgP/W2v/JOdcjnPuvuB2efDptb8DrwDfB0YC15pZ5+A+1zvnxhH4H++mWu1yFDOzccB1wInAScB3gMxQ+zrnXgBygSudc8c55/Y3cs7hwGXAeOfccUAVcGXw5XRgjnPuWOfcJy35WdoS/Srthy+dcwuC388HBgIdnXMfBtumAs/X2n9aveNfDf65GFjqnNsCYGbrgN7ATgJhfXFwv94E/rHY2ZIfQrx0KvCSc64EwMymAxOO8JwTgXHAPDMDSAW2B1+rAl48wvO3eQpuP5TV+r4K6Bhm/5JGjq+ud65qIMHMTgcmASc75/aZ2Uwg5TBrlbavI3V/Wz/UnxUDpjrn7gzxWqlzrupwCztaaKjET4XAbjM70PO5Gviwif3D6QDsDob2MAK/EosAfAxMNrM0M0sHLgbeBLqaWWczSwYurLX/XqBdmHPOAC4xs64AZtbJzPpGoPY2Sz1uf10D/N3M0oB1BMYhD9dbwH+Z2XJgJfBZC9QnbYBz7nMzexKYG2x6zDk3z8x+EWzbBKyodciTBH4u99PIxUXn3DIzuxt4x8zigAoC1100dXMz6ZF3ERHPaKhERMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouMULZtbdzJ41s7XBybDeMLMhZrY/OFHRMjN7yswSg/ufbmavB7+/1sycmU2qdb7JwbZLmnjPpOCEXWuCk3K9YmbZzahVU5tKRCm4JeZZYEKLl4CZzrmBwcmw7gS6AWuDExWNArKBSxs5zWLg8lrb3wQWhnnr3xB4CnCoc24w8DIwPVhPU65FU5tKBCm4xQdnABXOub8faHDOLQTyam1XEXiSr1cj5/gYOMHMEs0sAxgELGjsDYNPpF4H/PDA3BnOuScIzPVypqY2lWhScIsPRhKYFbFRZpZCYOrRtxrZxQHvAecAF3FwxsTGDAI2OueK6rXnAsc0dpCmNpXWoOAW3w00swXANmCLc25RE/s+S2C45HLgmVaorSm1pzZdENweEHxNU5tKkxTc4oOlBEIulANj3AOBcWb2tcZO4pybS2AsvItzblWY91wL9DGz+jPdjQvWU0nLTG16XPBrqHPu58HXNLWpNEnBLT54H0iuvaSamY0msOADAM65HcAdBC5aNuUO4K5wbxhcOGAqcH+tsedvAWnBerahqU0lShTcEvNcYArLi4FJwdsBlwL3Alvr7foykFZrnvJQ53rTOfdBM9/6TqAUWGVmq4FvABe7gArgwNSm7xJ6atMGFydr1bEMODC16aLgOXo0sy45ymlaVxERz6jHLSLiGa2AI0c9M3sJ6F+v+Xbn3NvRqEckHA2ViIh4RkMlIiKeUXCLiHhGwS0i4hkFt4iIZ/4/au+nPkD1pdYAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"col_x= \"CRIM\"\n",
"col_z = \"{}_Z\".format(col_x)\n",
"col_outlier = \"{}_Outlier\".format(col_x)\n",
"df_x = pd.DataFrame(df_xs[col_x])\n",
"std = np.std(df_x.values)\n",
"mean = np.mean(df_x.values)\n",
"print(\"mean={}, std={}\".format(mean, std))\n",
"\n",
"threshold = 3\n",
"df_x[col_z] = (df_x - mean) / std\n",
"df_x[col_outlier] = np.where(np.abs(df_x[col_z]) <= threshold, 'normal', 'outlier')\n",
"print(df_x.head())\n",
"\n",
"sns.catplot(x=col_outlier, y=col_x, data=df_x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Mean & Standard Deviation\n",
"\n",
"그래프를 보면 Z-Score 값은 Mean - 3 * Std ~ Mean + 3 * Std 와 같이 값의 범위로도 구할수 있습니다."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"mean=3.613523557312254, std=8.59304135129577, upper=29.392647611199564, lower=-22.16560049657506\n",
" CRIM CRIM_Outlier\n",
"0 0.00632 normal\n",
"1 0.02731 normal\n",
"2 0.02729 normal\n",
"3 0.03237 normal\n",
"4 0.06905 normal\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAFvCAYAAABq/iEqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAlPUlEQVR4nO3deXydVZ3H8c8v+9qmbdJ0pftqN2goLZsIRSsgBQSFQVkEOy4zAjoqOJsKo+iIDIijskkHGUAYoKBQ6MJWhJZ039u0dG/TdEm6pFnvmT/ubZqb3Cxtc3PvSb7v1yuv5pz7PM/9hYRvnpznOecx5xwiIuKPhFgXICIiJ0fBLSLiGQW3iIhnFNwiIp5RcIuIeCYp1gW0xrRp09zs2bNjXYaISHuzSJ1enHHv27cv1iWIiMQNL4JbREROUHCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHjGi7VKRCQOVZXDhtmQnAFDp0Ki4qS96L+0iJy8o/vgsYuhdGuw3e9suPUNSEyObV2dhIZKROTkLZl5IrQBdnwcPPuWdqHgFpGTV3W0cV/lkfavo5NScIvIyRt/AyRnnmhn94aRl8Wunk5GY9wicvJyh8GMt2Hpn4IXJyfeAmldY11Vp6HgFpFTkzcCPntvrKvolDRUIiLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnohrcZnaXma02s1Vm9qyZpZnZIDNbaGZFZva8maVEswYRkY4masFtZn2B7wAFzrkxQCJwPfAL4EHn3FDgIHBbtGoQEemIoj1UkgSkm1kSkAHsBi4GXgy9PhO4Kso1iIh0KFELbufcTuBXwDaCgV0GLAZKnXM1oc12AH2jVYOISEcUzaGSbsB0YBDQB8gEpp3E/jPMrNDMCktKSqJUpYiIf6I5VDIV+MQ5V+KcqwZeAs4DckJDJwD9gJ2RdnbOPeqcK3DOFeTl5UWxTBERv0QzuLcBk80sw8wMuARYA7wNXBva5mZgVhRrEBHpcKI5xr2Q4EXIJcDK0Hs9CvwQ+K6ZFQE9gCeiVYOISEdkzrlY19CigoICV1hYGOsyRETam0Xq1MxJERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPJLW8iYhIC2pr4OPHYNtH0H8STJoBicmxrqrDUnCLyOl78x5Y9Gjw8zWvwP4iuOLBmJbUkWmoRERO37L/bb4tbUrBLSKnLzO3QVvPiY0mBbeInL7P3geJKcHPE5Lhs/fGtp4OTmPcInL6Rn0B7loNO5dAnzMhOz/WFXVoCm4RaRtZPWHEtFhX0SloqERExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWkdgqWQ97Vsa6Cq9okSkRiY1ALbxwM6x9LdgedCH83QuQnBbbujygM24RiY0Nb54IbYBP3oMVz8euHo8ouEUkNsp2tK5PGlFwi0hsjPg8JKWfaCckwegrY1ePRzTGLSKxkdMfbvkrfPgbqK2GSTOg19hYV+UFBbeIxE6/iXDdU7GuwjsaKhER8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPRDW4zSzHzF40s3VmttbMpphZdzObY2YbQ/92i2YNIiIdTbTPuB8CZjvnRgLjgbXA3cA859wwYF6oLSIirRS14DazrsCFwBMAzrkq51wpMB2YGdpsJnBVtGoQEemIonnGPQgoAf5oZkvN7HEzywTynXO7Q9vsAfIj7WxmM8ys0MwKS0pKolimiIhfohncScBZwO+cc2cCR2kwLOKcc4CLtLNz7lHnXIFzriAvLy+KZYqI+CWawb0D2OGcWxhqv0gwyIvNrDdA6N+9UaxBRKTDiVpwO+f2ANvNbESo6xJgDfAqcHOo72ZgVrRqEBHpiJKifPx/BJ4xsxRgM3ArwV8Wfzaz24CtwJeiXIOISIcS1eB2zi0DCiK8dEk031dEpCPTzEkREc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4RaV/OQdlOCNTGuhJvRfUp7yIiYYrXwPNfgQOboEtf+OITMGBKrKvyjs64RaT9/PV7wdAGOLQTZn07tvV4SsEtIu2nZG14+8AmqKmMTS0eU3CLSPsZeml4e+AFkJQam1o8pjFuEWk/l/8KktNhywLocyZ87mexrshLCm4RaT9pXeHKh2Ndhfc0VCIi4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4plmZ06a2TXNve6ce6ltyxERkZa0NOX9RWBZ6APA6r3mAAW3iEg7aym4rwGuB8YBs4BnnXNFUa9KRDqf2mrYMBsqD8OIyyA9J9YVxa1mg9s59wrwipllAtOBB8ysB/DPzrl326E+EekMArXw1OWwfWGwnZUPX58PXfvFtq441dqLkxVAGXAIyALSolaRiHQ+m+afCG2AI8VQ+GTs6olzLV2cvJjgUMkkYC7wkHOusD0KE5FOpPpYhL6K9q/DEy2Ncc8FVgALgFTgJjO76fiLzrnvRLE2Eekshl0K3QfDgc3BdnIGnPXV2NYUx1oK7q8RvHtERCR6ktPhtrmw9GmoPATjroe84bGuKm61dHHyqXaqQ0Q6u8wecP6dsa7CCy2Ncb9GM2fczrkr27wiERFpVktDJb9qlypERKTVWhoqafJebTM7r+3LERGRlrQ0VJIIfAnoC8x2zq0ysyuAHwHpwJnRL1FEROpraajkCaA/sAh42Mx2AQXA3aFZlSIi0s5aCu4CYJxzLmBmacAeYIhzbn/0SxMRkUhamvJe5ZwLADjnKoDNCm0Rkdhq6Yx7pJmtCH1uwJB6bZxz46JWmYh0Tge3wNJnICEpOHuyS59YVxR3Wgru8UA+sL1Bf3+CwyYiIm2ndDv84UKoKAu2C5+Ab30EGd1jW1ecaWmo5EGgzDm3tf4HwZUCH4x+eSLSqax4/kRoQ3CVwDWzYldPnGopuPOdcysbdob6BkalIhHpvJIzWtfXybUU3DnNvJbehnWIiMD466HboBPt/DEw6guxqydOtTTGXWhmX3fOPVa/08xuBxa35g1Ck3gKgZ3OuSvMbBDwHNAjdIyvOueqTr50EelwMrrDNz+A9W9AQiIM/zwk67ktDbUU3HcCL5vZjZwI6gIgBbi6le9xB7AW6BJq/wJ40Dn3nJn9HrgN+N3JFC0iHVhKJoy9NtZVxLVmh0qcc8XOuXOBnwBbQh8/cc5Ncc61eFeJmfUDLgceD7UNuJjg0+MBZgJXnWLtIiKdUktn3AA4594G3j6F4/8X8AMgO9TuAZQ652pC7R0E10FpxMxmADMAzjjjjFN4axGRjqm1Dws+aaHFqPY651o1Ft6Qc+5R51yBc64gLy+vjasTEfFXq864T9F5wJVmdhnBp8J3AR4CcswsKXTW3Q/YGcUaRCQeBQJQth269IXEaMZQxxS1M27n3D3OuX7OuYEEnxQ/3zl3I8Ehl+NXHm4GdHe9SGeyewU8PAEeGgcPfgq2fBDrirwTteBuxg+B75pZEcEx7ydiUIOIxMrr/wSlW4OfH9kDr/5jbOvxULv8jeKcewd4J/T5ZmBSe7yviJyG6gqY+2PY+CbkjYTP3gc9hpz+cUvWhbcPbIKaKkhKOf1jdxKxOOMWER/MvxcW/g4ObIb1r8Nzf9c2xx32ufD24M8otE+SrgqISGQb54S3S9ZB6TbIOc3bcy9/AFKzYcsC6HsWXHrv6R2vE1Jwi0hk+aNh3/oT7YwekJV/+sdN6wJX/Pr0j9OJaahERCK79KfQK/SslMw8mP7fkJQa25oE0Bm3iDQl5wz4xvtweE/wbDsxOdYVSYiCW0Sal90r1hVIAxoqERHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm5p0pJtB1m89QDOuViXIiL1JMW6AIk/VTUBbn1qER8U7QfgrDNyeOb2yaSnJMa4MhEBnXFLBG+u3lMX2gBLtpUya9nOGFYkIvUpuKWRksOVreoTkdhQcEsj08b0IrPesEhqUgKXj+sdw4pEpD6NcUsjfXLSeeEb5zLzb1uoCThumjKAwXlZsS5LRELMhzsGCgoKXGFhYazLEBFpbxapU0MlIiKeUXCLiHhGwd1JbSw+zP8t3sG2/eWxLkVETpIuTnZCT3+4hX+dtRqAxATjoesncMW4PjGuSkRaS2fcnUwg4Hhgzoa6dm3A8et6bRGJfwruTibgHOWVtWF9ZeXVMapGRE6FgruDKNp7hB+/upofv7qaor2Hm9wuKTGBL5/dP6zvQHkVs1ftiXaJItJGFNwdwO6yY1z92w946m9beOpvW7jqt39jZ+mxJrf//udGkJhw4vZQ5+CR+Rvbo1QRaQMK7g7gryt2c7iypq59pLKGv67Y1fQOEW7pX198mN1lTYe9iMQPBXcH0CU9uVFf1wh9ddunJTN1VH5YX3Wt44n3P2nz2kSk7el2QI/NWraTJz/YQgIwsEcGW0L3ZI/p24Urx/dtdt8bzu7Pm6vDx7VLjmgFQBEfKLg9tXjrAe54blldO8Hg/mvG0jsnnfOH5oaNYUcyZWgP+uak142Fm8HVZzYf9iISHxTcnnp7XUlYO+DgaFUtnx6e16r9U5MSeeEbU3js/c3sO1LFF8/qy0UjekajVBFpYwpuTw3Lb7zM6rCerV96dU9ZBQuK9nHFuN5MHNC9LUsTkShTcHvqinF9eHdDCa8s3UmCGV+ZPIALhuW2at+PNu/n5icXUVkTAODrFwziny8fHc1yRaQNKbg9lZhgPHDdeMb368rKnWWM7du11fs+Mr+oLrQB/vjBFr550VC6Z6ZEo1QRaWMKbo/dP3sdf3h3MwAvLt7JhuLD3HPZqBb3K6+qCWvXBByVNbVNbC0i8Ub3cXvsmY+2hbcXbmtiy3BfnTIgrD11VD69u6a3WV0iEl064/ZYVmoSR+rNmMxKbd238+oz+5GXlcbctcUMycvkuoL+Le8kInFDwe2pQxXVfKmgH795uwjngvdhf++zw1u9//nDcjm/lRczRSS+KLg99NcVu/mnF5ZzrLqWbhnJ3DRlINMn9NGT2EU6iaiNcZtZfzN728zWmNlqM7sj1N/dzOaY2cbQv92iVUNHVFMb4N9fXcWx6uDFxIPl1Xy4ef9JhXZZeTV7yiqiVaKIRFk0L07WAN9zzo0GJgPfNrPRwN3APOfcMGBeqC2tdKy6ln1HqsL6dhxo/XMjH3hrPQX/MYfJP5/H1576mGNVuptExDdRC27n3G7n3JLQ54eBtUBfYDowM7TZTOCqaNXQEWWnJTeaaDOkZxY1tYEm9jhh1c4yfjO/iOpaB8D8dXt5ZuHWqNQpItHTLrcDmtlA4ExgIZDvnNsdemkPkN/UfhLZIzecxTmDTkxTf3/jPu5+aWWL+20qOdKqPhGJb1EPbjPLAv4PuNM5d6j+a845B7gm9pthZoVmVlhSUhJpk06ra0ZyoyVYX166M+zWwEjOHZJLWnL4t/ySkfq9KeKbqAa3mSUTDO1nnHMvhbqLzax36PXewN5I+zrnHnXOFTjnCvLyWrfiXUf13KJtnHf/fArum8t/v1MEQEZKYtg2KYkJJLWwlGtedir/87VzOH9oLuP6deX+a8YydbSCW8Q3FjzpjcKBzYzgGPYB59yd9fr/E9jvnLvfzO4GujvnftDcsQoKClxhYWFU6ox3q3aWccVvFoT1PXlLATW1jm/8aTGB0Lfv6jP78uCXJ7R/gSISTRHPxqJ5xn0e8FXgYjNbFvq4DLgfuNTMNgJTQ21pwsdbDjTqW/jJAXYfOlYX2gCvr9zNfj3BRqRTiNoEHOfcApr4bQFcEq337Wgm9M9p1Hdm/xx+8tqasL7KmgBLtpVy6WkOfVTVBHjgrfXMWVvM4NxM7rlsFEM0sUckrmiRqTh35hnd+JfLR9E1PZmMlES+ddEQJg7ozu4IE2g+1afLab/fw/M28of3NrO55Chz1+7l9pmFBALRGU4TkVOjKe8euP2Cwdx2/iAAzIyy8mqSE63ufmyAwbmZ9Mk5/RX+3l4ffq34k31H2bL/qKbTi8QRnXF7wswIXu8N3g74tVCQQ/COkp9M/9RJH3P7gXL+/PF2VuworesbkZ8dtk12WpKWfBWJMzrj9tQ9nx/FZ0fns7H4COcPy6Vft4yT2n/+umL+/unFdWftd00dzh1Th/H9aSMoKjnCih1ldMtI5j+uHkt6g1sPRSS2onY7YFvqzLcDRsv0RxawfEdZXTstOYEl/3opGSnB3+XFhyrIyUgmNUmhLRJD7X47oETJuxv28od3N1F86NgpH6O8weJSVTWBsDHz/C5pCm2ROKXg9khNbYDLHnqPm5/8mJ+/sY7JP5vPa8t3AbBm1yFmr9rDoYrqVh2r4ePLrprQl67pyW1es4i0PY1xe6Bo7xGWbD1IeVUNa3Yfrut3wE9eW83y7aU8vuATALqmJ/PcjMmM6t38rYE3TRlIv27pvLdhHyN7ZfPFif2i+SWISBvSGHece3HxDr7/4nKa+jalJBo1ARc2i3JU72yevu0ccrNS26dIEYkWjXH76NdvrW8ytAEuHJ5Hw/kxa3cf5oqHF1BaXhV5JxHxmoI7zpVXN/2EmukTejN9Ql96Zjc+s95zqILXVuyOsJeI+E7BHeeuP7t/k6/NXlXMPz67lL2HIy8udayq8frcJYcr+funC5nw07e46clFbD+Jx56JSHxQcMe55tYfqawJf1xZYoPRsF/OXse8tcVhff/88kreXF1MaXk1720o4Y7nlgJw8GgVFc2c3YtI/FBwx7mUk7iXOjM1/CahmgD84o11YX0fbd4f1l6yrZRb/7iIM++dw8R75/D4+5up1aJSInFNwR3nLh2VT7eM1t1fnZzY+Nu572j4Bcpx/XLC2rlZKby9PvhouKNVtdz317UU3DeHWct2nlrBIhJ1Cu44l5BgzP3up+kbWvkvwWBsny6M6dt4CKVLhAk0V43vE9b+j6vHMD60xveI/GxG9mp8nIPl1Xz/hRV6MINInFJwe2Deur3sLA1Obw84WLnrENec2bfRducNzWVs365hfX9evIN36i3VOqBHJrO+fR7r7p3Gm3ddyJUNgv24qtoA64sPR3xNRGJLwe2BjRECNDkxgfOH5ta1e2an8q2LhvCn284hr97EmyOVNfz41dWN9k9LDo6dX1fQjx9MG0GPzJSw17NTkxoNq4hIfFBwe+AzI3qGtZMTjQuH5zHza5P49y+MZkL/HEb27sL7G0u4+IF3KGkwxHH8bD0SM+NbFw1l4Y8u4crxvclOS2JEr2wev7mArFStiCASj/R/pgfOHZrLf147jicWfMLusgqOVtZw5/PL+MHnRvKrN9dzNLTS33sbSiLuf/nY3gCUV9Wwae9RhuVn1Z1xH/dfczfy6vLghJ2ivUc4cFSzLkXilc64PXFdQX+G9syi7Fg1NQHH0m2l3Pn80rrQbsoV43rzs2vG8t6GEs752Ty+8MgCJv98XthtgeVVNTz2/ua6dm3A8cjbRVH7WkTk9Ci4PbLwk/B7sIsPNb7rI6HeJJwheZk8+OUJZKQk8W+zVnG4IjiTsrS8OmzcO+BodO922bHWLQ8rIu1PQyWeqA04KqrCZ0rmZiWTnJgY9sT3BAtecByUm8X1Z/cnOTEB5xzbD4aPc9ef6p6VmsQ5g7rzwaYTvxhKDldSVl5N11beQy4i7Udn3J4o3HKAw5Xha4+UldeEhTYEZ0vOXlXMZWN6k5MRvFPEzJg2plfYdp8PjXsfl9dgoarKmgAfNphlKSLxQcHtiYbT2QGqm5iaXnasmofmbaxrF+09zDcuHMyMCwdz9sBufPOiIdw7fUzYPsMaPN0d4MXF2/ni7/7G4+9vxod120U6Cw2VeKJHVgo9s1PrVgLMSk3kSGXTFyYXFJVww2MfsnV/ObtKg2flU0f15OZzB/Dykl3MeLqQW84dyCWj8gG45dyBfLR5P+9v3EdyopGZksTctcGJO4u3HiQxwbj1vEFR/ipFpDUU3J646/llYcu3FgzszqjeXfjDu5sIuOC93fUf9lt8qLLRxcu5a/fWhTHAgo37+MG0Edx+wWBKj1UzsEcGyYl5TBzQjf98c0PYvm+s2qPgFokTCu44V1Mb4KF5G/lo84Gw/oWbD3DBsDzuuGQYkwf34IweGVz+8IKTuv/aAb+YvZ5Zy3axsfgwx3N//roSkhKCj0Q7bmCPjLb4ckSkDSi449zD84v4zfzG91TXBALc+5c1APTN2cHr37mAntmppzRxZt2exlPqR/TKZuPeI1TVBBjaM4s7pg4/+eJFJCoU3HFuzpriRn3dM5I5UH7iPuudpcd4bcUubjt/EN9/cUWbvO+kQd155vZz2Hu4kmE9szCL+MxSEYkB3VUS54bkZYa1zQgL7eMSzLiuoD+fb3DbX2skJoSHclpyAsN7ZpGZksjw/GyFtkicUXDHuR9OG8nQnllAcHJNpLvy+ndP54rxwfuyh+dn09qYHRAat64NODJTEklPTiAl0aioDnDPy6sY8a+z+cvyXW3xZYhIG1Jwx7n+3TOYc9eFvPKtcyOGNgSfktMlLZk5a4p5aN5GWnPHdVZqElv3n5g9ebSqlilDcqmqd2dKwME/PLuU99ZHXrxKRGJDwR3nlm8v5ZH5Rdz4+MImA/lPH23jSGUNH27a1+i1kb0aT6xJS0rgxnPOaNRftDfygxNmPF3I4QqtXSISLxTccewXs9cx/bcf8MCcDc2uAljrHLW1jl0R1t2+bGzjMe/rJ53BbecPCltv24BtByKv211RE2DljrKT/wJEJCoU3HHq4NEqHntvc8sbEnzgb3pKInsirBaYm5XaqK9bRgo9u6Tx3IzJXDKqJxnJic0OryQlGMMjnLmLSGwouONURU1t2ASY5hQfquQvK3Yxuk/4g3+zU5P4wrg+XDQir65vYI8Mbpx8Bv/9ThHXP/oR89ftpby68dl8Yr0rnDUBx8IGE4BEJHZ0H3ec6t01nUtG9mTeur0tbwzsLqvge5cO55OSo3y4eT952ancd9UYstOTeerWSXy85QBHKmo4b2guK3eW8svZ65s9Xm2D3xlPLNjM5eN6R95YRNqVgjuO/fbGs3h20TaWby/llWXN35bXp2saG/ce4Znbz+FwZQ2ZKYkkJZ74g2pYzyyWbiul5EglHxQ1vojZkqQE/XEmEi8U3HEsLTmRW88bxJZ9R1oM7rv+vByA1KQERvfO5oZJA5g2phf/NmsVry7fRf1Rl9SkxiGcnAApSYkRL4ImJhh//+nBp/fFiEibUXB7oF+3DDJTIodqQ5U1AZZuL2Pp9hXc/dIKIg2TV9YEGvVVB2BYj0zW7D5U15ecaHzz00O4ckIfhvbUxUmReKHg9kBSYgK/vHYc//Ds0rpJOMkJcPGofCqqA7zbxNPdW3lts86a3Yf44bSRvLN+LxkpiXzrM0M5e2D306xeRNqagtsTm0uOhs2crA7AoWM13DV1WJPBfSouHJ7LNy8a0mbHE5G2p+D2wAuF2/n1nA2N+j/cvJ8PH22750JeNCKPT/Xp2mbHE5HoUHB74JG3i1q1/sip6paRzL3Tx/C5U1hZUETan+7x8sDRBk93P1WRVg3skpbEz68ZS+HWg/zgxRVNrlciIvFDZ9we6NctnX1HTv7JNg1FOmvvlpHCt59ZUjfh5pWlO/nfr5/DlCG5p/1+IhIdOuP2wFlndIvasbceKA+bJemAn7y2JmrvJyKnT8HtgdTkxBa3GZyb2aivW0byKb1fWw3NiEh0KLg9sPNg5OVWj/vOxUMjzmw8GOERZ63x1SkDTmk/EWkfGuOOY68u38XLS3ZwpJkz4G6ZySQmGD9to+GNQbmZzLhQ93GLxDMFd5yavWo333l2aV07KzWJgAtQXhU+Xf3g0WoenLuxzd5358Fy5qwp5tLR+dTUBig7Vk2PCGt6i0jsKLjj1GvLd4e1mzvrbktVtY4fvbSCFwq78d7GEiqqA0zon8PvvzKRXl3T2qUGEWmexrjjVJ+ctg/JSKsCRlJypIq31hRTUR08u1+2vZT731jb5vWIyKlRcMepaJzdju/bJeIknNZYt0cTc0TihYZK4tTHnxxs82Mu2lp6yvteODyv5Y1EpF3ojDtO9chKiXUJdRIMbpx0RqzLEJGQmAS3mU0zs/VmVmRmd8eihni3ckdprEuoE3Bw8x8XxboMEQlp9+A2s0Tgt8DngdHADWY2ur3riHdr42xMecv+8liXICIhsTjjngQUOec2O+eqgOeA6TGoI64FTvbxNSLSacQiuPsC2+u1d4T6wpjZDDMrNLPCkpK2e8KLLwbnNV57JJYSTvV2FBFpc3F7cdI596hzrsA5V5CX1/nuaPjzjMmxLiHMtWf1i3UJIhISi+DeCfSv1+4X6pN6umWl8afbJsXFb9bbzx/EL68bH+syRCTEnGvfsVQzSwI2AJcQDOyPgb9zzq1uap+CggJXWFjYThWKiMSNiIOU7T4BxzlXY2b/ALwJJAJPNhfaIiISLiYzJ51zrwOvx+K9RUR8Fw9DqCIichIU3CIinlFwi4h4RsEtIuIZBbeIiGcU3CIinlFwi4h4RsEtIuIZBbeIiGfafa2SU2FmJcDWWNfhsVxgX6yLkE5JP3unZ59zblrDTi+CW06PmRU65wpiXYd0PvrZiw4NlYiIeEbBLSLiGQV35/BorAuQTks/e1GgMW4REc/ojFtExDMKbhERzyi4pVlmtsXMcmNdh/jBzG4xsz712u+YWUHo89fNLCdmxXUgCu4OLPRgZpH2dAvQJ9ILzrnLnHOlrT2QmSW2UU0djoI7zpnZQDNba2aPmdlqM3vLzNLNbIKZfWRmK8zsZTPrFtr+HTP7LzMrBO4ItR80s8LQcc42s5fMbKOZ3VfvfV4xs8Wh95gRsy9Y4o6ZfdfMVoU+7gz9TK6q9/o/mdmPzexaoAB4xsyWmVl6g+PU/fVmZl8xs0Wh7f5wPKTN7IiZPWBmy4Ep7fhlekXB7YdhwG+dc58CSoEvAv8D/NA5Nw5YCfx7ve1TnHMFzrkHQu2q0Oy13wOzgG8DY4BbzKxHaJuvOecmEvwf7zv1+qUTM7OJwK3AOcBk4OtAt0jbOudeBAqBG51zE5xzx5o45ijgy8B5zrkJQC1wY+jlTGChc268c25BW34tHYn+lPbDJ865ZaHPFwNDgBzn3LuhvpnAC/W2f77B/q+G/l0JrHbO7QYws81Af2A/wbC+OrRdf4K/LPa35RchXjofeNk5dxTAzF4CLjjNY14CTAQ+NjOAdGBv6LVa4P9O8/gdnoLbD5X1Pq8FclrY/mgT+wcaHCsAJJnZRcBUYIpzrtzM3gHSTrFW6fhyCP9r/WR/VgyY6Zy7J8JrFc652lMtrLPQUImfyoCDZnb8zOerwLvNbN+SrsDBUGiPJPgnsQjA+8BVZpZhZpnA1cAbQE8z62FmqcAV9bY/DGS3cMx5wLVm1hPAzLqb2YAo1N5h6YzbXzcDvzezDGAzwXHIUzUb+IaZrQXWAx+1QX3SATjnlpjZU8CiUNfjzrmPzeynob6dwLp6uzxF8OfyGE1cXHTOrTGzfwHeMrMEoJrgdRct3dxKmvIuIuIZDZWIiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt3jBzHqZ2XNmtim0GNbrZjbczI6FFipaY2b/Y2bJoe0vMrO/hD6/xcycmU2td7yrQn3XNvOeKaEFu4pCi3LNMrN+rahVS5tKVCm4Je5ZcEGLl4F3nHNDQoth3QPkA5tCCxWNBfoBX2riMCuB6+u1bwCWt/DWPyM4C3CEc24Y8ArwUqie5tyCljaVKFJwiw8+A1Q7535/vMM5txzYXq9dS3AmX98mjvE+MMnMks0sCxgKLGvqDUMzUm8F7jq+doZz7o8E13q5WEubSiwpuMUHYwiuitgkM0sjuPTo7CY2ccBc4HPAdE6smNiUocA259yhBv2FwKea2klLm0p7UHCL74aY2TKgGNjtnFvRzLbPERwuuR54th1qa079pU2XhdqDQ69paVNploJbfLCaYMhFcnyMewgw0cyubOogzrlFBMfCc51zG1p4z03AGWbWcKW7iaF6amibpU0nhD5GOOd+HHpNS5tKsxTc4oP5QGr9R6qZ2TiCD3wAwDm3D7ib4EXL5twN/KilNww9OGAm8Ot6Y883ARmheorR0qYSIwpuiXsuuITl1cDU0O2Aq4GfA3sabPoKkFFvnfJIx3rDOfd2K9/6HqAC2GBmG4HrgKtdUDVwfGnTOURe2rTRxcl6dawBji9tuiJ0jN6trEs6OS3rKiLiGZ1xi4h4Rk/AkU7PzF4GBjXo/qFz7s1Y1CPSEg2ViIh4RkMlIiKeUXCLiHhGwS0i4hkFt4iIZ/4f7iamy+QT8m8AAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"col_x= \"CRIM\"\n",
"col_outlier = \"{}_Outlier\".format(col_x)\n",
"df_x = pd.DataFrame(df_xs[col_x])\n",
"std = np.std(df_x.values)\n",
"mean = np.mean(df_x.values)\n",
"\n",
"threshold = 3\n",
"upper = mean + std * threshold\n",
"lower = mean - std * threshold\n",
"print(\"mean={}, std={}, upper={}, lower={}\".format(mean, std, upper, lower))\n",
"\n",
"df_x[col_outlier] = np.where((df_x < upper) & (df_x > lower), 'normal', 'outlier')\n",
"print(df_x.head())\n",
"\n",
"sns.catplot(x=col_outlier, y=col_x, data=df_x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Modified Z-Score\n",
"\n",
"평군과 표준편차를 이용하는 Z-Score 는 데이터의 크기가 12 이하로 작거나, 데이터의 Skew 가 큰경우 제대로 동작하지 않는 경우가 많습니다. 그래서 평균 대신 중앙값을 이용하는 Modified Z-score 가 주로 사용됩니다.\n"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"median=0.25651, median_abs_std=0.22145000000000004\n",
" CRIM CRIM_Z CRIM_Outlier\n",
"0 0.00632 -0.76204 normal\n",
"1 0.02731 -0.69811 normal\n",
"2 0.02729 -0.69817 normal\n",
"3 0.03237 -0.68269 normal\n",
"4 0.06905 -0.57097 normal\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAFvCAYAAABq/iEqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAk60lEQVR4nO3deXiU1d3/8feXhB0B2XdRNhFkkeBeq6CttSqiVrFuqK1dHm3V1qfqY/u0T/vrqlXb2lqrVWvdFZdailtR1KoYFWVTQZBNdtmXhCTn98eZODOZmUwSMnPnTD6v65orcy9zzzeWfrg591nMOYeIiISjRdQFiIhI/Si4RUQCo+AWEQmMgltEJDAKbhGRwBRHXUBdnHjiiW7GjBlRlyEikm+WbmcQd9wbNmyIugQRkSYjiOAWEZE4BbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CKSfxsWwTt/h/UfRF1JkIKYZEpECsicB+CJbwEOMDjlZhg3NdqaAqM7bhHJr5n/Dx/a+J///lmU1QRJwS0i+VW2LXm7fEc0dQRMwS0i+TX+a8nbJRdHU0fA1MYtIvk14XroMRyWvwb9xsOos6OuKDgKbhHJLzM4+Ez/kgZRU4mISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigclpcJvZlWY238zmmdkDZtbGzPY3szfMbLGZPWRmrXJZg4hIoclZcJtZX+A7QIlzbiRQBEwBfgXc5JwbDGwCLslVDSIihSjXTSXFQFszKwbaAauBCcCjseP3AKfluAYRkYKSs+B2zq0CbgCW4wN7C/AWsNk5VxE7bSXQN1c1iIgUolw2lewLTAL2B/oA7YET6/H5S82s1MxK169fn6MqRUTCk8umkuOBpc659c65PcA04Cigc6zpBKAfsCrdh51ztzvnSpxzJd27d89hmSIiYcllcC8HDjezdmZmwERgATATODN2zoXAkzmsQUSk4OSyjfsN/EPIt4G5se+6HfgBcJWZLQa6AnfmqgYRkUJkzrmoa8iqpKTElZaWRl2GiEi+WbqdGjkpIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhKY4uyniIg0wNbV8NofYPtaGHU2DDkh6ooKhoJbRBpf5R6460uwaanfnvsIfPURGPqFaOsqEGoqEZHGt/y1eGhXe/f+aGopQApuEWl87dOsE5tunzSIgltEGl+P4TBuany7Yz848vLIyik0auMWkdw45RYY/3X/cHLg0VDcOuqKCoaCW0Ryp9dIYGTUVRQcNZWIiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIhKtqipY9RZs+jjqSoKhSaZEJDrb18PfToV1CwCDw78NJ/486qqaPN1xi0h0XvtDLLQBHLx+K6x7P9KSQqDgFpHobFlZt32SRMEtItEZeUbydoeeMPCoaGoJiNq4RSQ6B54EX7kb5tzv16Q8+ipo2Tbqqpo8BbeIRGvEZP+SOlNTiYhIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiAQmp8FtZp3N7FEze9/MFprZEWbWxcyeM7NFsZ/75rIGEZFCk+s77luAGc65A4HRwELgGuAF59wQ4IXYtoiI1FHOgtvMOgHHAHcCOOfKnXObgUnAPbHT7gFOy1UNIiKFKJd33PsD64G7zOwdM7vDzNoDPZ1zq2PnrAF6pvuwmV1qZqVmVrp+/foclikiEpZcBncxcAjwJ+fcWGAHNZpFnHMOcOk+7Jy73TlX4pwr6d69ew7LFBEJSy6DeyWw0jn3Rmz7UXyQrzWz3gCxn+tyWIOISMHJWXA759YAK8xsWGzXRGAB8BRwYWzfhcCTuapBRKQQFef4+pcD95lZK2AJcBH+L4uHzewSYBlwVo5rEBEpKDkNbufcHKAkzaGJufxeEZFCppGTIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIiKBUXCLiARGwS0iEhgFt4hIYBTcIlJ329bCnl1RV9HsKbhFJLudn8JdJ8GNQ+GGofD2vVFX1KwpuEUku1m/gWWv+vdlW+GfV8GODdHW1IwpuEUku3ULk7cry2HjR9HUIgpuEamDISckb7fvDn3GRFKKQHHUBYhIAA77FpRth3mPQad+cPz/QnHrqKtqtsw5F3UNWZWUlLjS0tKoyxARyTdLt1NNJSIigVFwi4gERsEtIhIYBbeISGAU3CIigVFwi4gERsEtIhIYBbeISGAU3CIigal1yLuZnV7bcefctMYtR0REssk2V8mjwJzYC5KHXzpAwS0ikmfZgvt0YAowCngSeMA5tzjnVYlI07VhESydBb1HQ7+SqKtplmoNbufcE8ATZtYemATcaGZdgf9xzr2Uh/pEpCmZNw0euwRcld+ecD0cc3W0NTVDdX04uRvYAmwFOgBtclaRiDRds34TD22Al2+CirLo6mmmsj2cnIBvKjkUeB64xTmn+VVFmquaCwVXlicHueRFtjvu5/Gh/QrQGrjAzH5X/cp5dSLStBz2jeTtQ86Hlm2jqaUZy/Zw8mJ87xERETj8W9B1MCx5EXqNgoO/EnVFzVK2h5N356kOEQnFkBNS16CUvMrWxv0Parnjds6d2ugViYhIrbI1ldyQlypERKTOsjWVZOyrbWZHNX45IiKSTbamkiLgLKAvMMM5N8/MTgauA9oCY3NfooiIJMrWVHIn0B+YDfzOzD4BSoBrYqMqRUQkz7IFdwkwyjlXZWZtgDXAIOfcxtyXJiIi6WQbgFPunB8W5ZzbDSxRaIuIRCvbHfeBZvZe7L0BgxK2cc6NylllIlLYlr0G7z8N+w6EsedpBGY9ZAvu0UBPYEWN/f3xzSYiIvW34Cl4+AI+Gyby4Qw477FISwpJtqaSm4AtzrlliS/8TIE35b48ESlIb/6FpLF9i5+HT5dEVk5osgV3T+fc3Jo7Y/sG5qQiESl8LdvV2GFQrNmi6ypbcHeu5ZgapESkYY6+EooTImTcVOjYJ7JyQpOtjbvUzL7unPtL4k4z+xrwVl2+IDaIpxRY5Zw72cz2Bx4Eusaucb5zrrz+pYtIsAYcDpe/5ZtIuuwP+x8TdUVBMecyz9pqZj2Bx4Fy4kFdArQCJjvnsj6gNLOrYp/pGAvuh4FpzrkHzew24F3n3J9qu0ZJSYkrLdX6DSLS7Fi6nbU2lTjn1jrnjgR+Anwce/3EOXdEHUO7H/Bl4I7YtgET8KvHA9wDnFan8kVEBMjeVAKAc24mMLMB178Z+G9gn9h2V2Czc64itr0SPw9KCjO7FLgUYMCAAQ34ahGRwlTXxYLrLTYZ1TrnXJ3awmtyzt3unCtxzpV07969kasTEQlXne64G+go4FQzOwm/KnxH4Bags5kVx+66+wGrcliDiDQFlXtg6yfQqT+0yNn9YrORs/+CzrlrnXP9nHMD8SvF/9s5dy6+yeXM2GkXAk/mqgYRaQKWvgw3jYBbRsHvx8KaeVFXFLwo/ur7AXCVmS3Gt3nfGUENIpIPzsFTl8H2tX5708cw/epISyoEuWwq+Yxz7kXgxdj7JcCh+fheEYlYRZkP60TrF8bfr3sfnvshbPwIhp8Mx10Pxa3yWmKI1NgkIrnTsg3s//nkfUNP9D+rKuH+r8CiZ+HTj+DVW+BlLXNbFwpuEcmtM+6AUVOg2zAY/zU46Td+/4YPYfPy5HMXPZf/+gKUl6YSEWnGOvSA0/+cur9Tf2i1D5Rvi+/rcVD+6gqY7rhFJBqtO8Ck30PbLn6733iY+MNoawqE7rhFJDojJsOwL8OuTbBPz6irCYbuuEUkWsWtFNr1pOAWEQmMgltEJDAKbhGRwCi4RUQCo+AWEQmMgltEJDAKbhGRwCi4RUQCo+AWEQmMgltEJDAKbhGRwCi4RUQCo+AWEQmMgltEJDAKbhGRwCi4RUQCo+AWEQmMgltEJDAKbhGRwCi4RUQCo+AWEQmMgltEJDAKbhGpXfkOWPw8fLo06kokpjjqAkSkCVv9HvxtEuz6FDCY+CP43FVRV9Xs6Y5bRDJ78Zex0AZwse1NkZYkCm4Rqc32tcnblWUK7iZAwS0imY2ekrzd/zDockA0tchn1MYtIpkd+nVo3RHefxq6DYEjLou6IkHBLSLZjD7bv6TJUFOJiEhgFNwiIoFRcItI3ezYAO89DCtmR11Js6c2bhHJ7pN34O5ToHyb3y65BE7+bbQ1NWO64xaR7F7+bTy0AUr/CptXRFdPM6c7bhHJrmxbjR3Oz2GybQ28/0/o0BOGnghFipR80H9lEcmu5CJYMjO+PeBIcFXwh/FQttXvGzQRzp9W/2t/ugRm3wGV5TBuKvQa2SglFzIFt4hkd9AkuOApWPgUdN4PSi6GZ66NhzbARy/Ayreg37j019iwGDYvg/2OhJZt/b4dG+AvE+LD6N/5O3zzFeg2OLe/T+AU3CJSNwd83r+qVe5JPaeyPP1nX/gpvHyDf9++B0x9GroP838RJM59UrEL5j4Cx13beHUXID2cFJGGKbkEilrFt/sc4ucyqWnrangloQfKjnUw6zf+fdt9U89v27lRyyxEuuMWkYbpPx6+MQvmPeYfTo4+B1qkuRec96hvD0+0fZ3/OezLMOAIWP6a3+4+HMZ8Nbd1FwAFt4g0XI/hMOH6zMdXvwvP/jB1/+hz/M/iVjB1Onw8CyrKYdBxUNQyN7UWEAW3iOTOoucAl7xv5Bkw5pz4dosWcMCx+awqeApuEWkc5Tvhwxm+3XvIF/zddPcDU88beUb+ayswCm4R2Xs7P4U7Jvo+2QC9R8PFz8Kwk+CQC303P4BDzoehX4quzgKhXiUisvfm3B8PbfBt2+8/7ZtBTv0dXL0YTr4ZMHjnXqiqjKrSgqA7bhHZe3t2pu4r3xF//+adMPNn/v1bd8HqOXDyTXkprRDpjltE9t6os/wSZ9U69IThp8S3S/+afP47f/e9SKRBdMctIntv34Fw6Yu+GaSoNRxyAbTrEj/eugMkzlPVsh20KMpzkYVDwS0ijaPrIDj+x6n7P13qJ4969ofgYm3bx12n4N4LCm4RyQ3n4PFvwnsP+u1+h8LY86D/oX7gjjRYztq4zay/mc00swVmNt/Mvhvb38XMnjOzRbGfaSYrEJHgffTveGgDrJwNVRXZQ3vbGt+9UDLK5cPJCuB7zrmDgMOB/zKzg4BrgBecc0OAF2LbIlJoNi+r275qFWXw0Hlw4zC4YQg8W8tQ+mYuZ8HtnFvtnHs79n4bsBDoC0wC7omddg9wWq5qEJEIDfmifwhZzVrA8EmwshRmXAf/+T3sTpjPe859sPAf/n1VhT++/I381hyIvLRxm9lAYCzwBtDTObc6dmgN0DMfNYhInnXqCxf+A169BSp2w/iv+3Ur750cny1w3jT4+r/BDNZ/mHqNDR/AgDRTxTZzOe/HbWYdgMeAK5xzWxOPOeccKTPQfPa5S82s1MxK169fn+syRSQX+pXA2ffCuY/A0C/4/tyJU7x+8jasetu/H/rF5M8WtYYDjstfrQHJaXCbWUt8aN/nnKtejG6tmfWOHe8NrEv3Wefc7c65EudcSffu3XNZpojUR0UZ/OMK+MUA+OORsOTFun+2ZfvUfa1izSmDjoPTboO+42Dg5+Dch6Fz/8aouODkrKnEzAy4E1jonEtY/oKngAuBX8Z+PpmrGkQkB169xQ9bB1i3BR46H65aAK33SX/+rs3wz+/5Xib7DoRWHaB8uz824vTkXiZjzkme8lXSymUb91HA+cBcM5sT23cdPrAfNrNLgGXAWTmsQUQa27JXk7fLtsKaebDfEenPf+Y6vwoOwK5PoesQv9jwmvegY18/OVWXA3Jbc4HJWXA7514BLMPhibn6XhHJsX7jk5tHWrarvW/20peTtzcu8mtQ7og9u/rP72Cf3tDrYPjCTxXidaBJpkSkfo6+EkaeCVYEnQbAGXfWvsBvnzHJ2227xEMb/Mrwm5f5aWAf0HqTdWG+Y0fTVlJS4kpLS6MuQ0QSVVWlXxy4pi2r4LGvwfL/QNfBfgWcl36V+fwr5kLnAY1XZ9jStlporhIRaZi6hDb4/twX/wv27IKWbWHTCnjnPti6MvXctl38lLBSKzWViEh+tGwLn8yBPx0RD+2+JdBzhH/frhtMuhWKW0dWYih0xy0i+fPqzX70ZLVVpfCdOT6s23XzCwxLVrrjFpH6+XSp78u95OXs59ZUnmaJsz07oWMfhXY96I5bROrutVt9v+xqXQfDaX/yc2zXRcnFsOhZPpvpYsAR8aYSqTP1KhGRutm2Bm4aCVV7Uo+NORdO+2Pq/soKKKpxf7j8dZj/hO85csgFflkzyUS9SkSkgTYsgjtOSB/a4KdkPfLy+ECc+U/AjGt8f+0Rk+HU3/uHkwADDvevaltWwXsPQXEbGD0lea1KSUvBLSLZvXYr7N5U+znVq9bs2AjTLoXKMr899xE/zP3YH6R+ZvNy+PMxsCt27Tdug2/9R3fhWSi4RSS78h21H+82NH4XvXZePLSrLXjC7xt+qh/SPusG2PSxn3BqV8JfCJuXwVt3w5GXNWLxhUfBLSLZjZsK8x6Lr9LecyQccTm8e79/uHj0VfFV23uP9tO37kkI+3UL/OuVm/3d9O4tmb/r2f+BLSvhS7/M1W8TPD2cFJG6WfUWzH0UOvSAFsXw3I/8ogjFbWDKfdB7LLRqDy3b+Clcn7neD7SpLaTBz3lS/RdCoivnQ6d+ufldwqGHkyKyF/qO800ixW3gN4PiK9lU7IZHpkLZNmi1D5zwExh/CXz7P/6h5h9Kar9uq/Z+atiatq1RcGegATgikt2GRXDb0fCLfvCnI6Fse/LxsthoyPJtMP1q31MEoNsQ36ukNmVboahl8r6i1tBnbOPUXoAU3CKS3T++C2vm+vcbPqy914erhPXvx7fP+Gv28K7cA2339e/bdYGvPhJvM5cUCm4RyW71u8nbu7dAh17pz23dKXkkZYsWcMrvYPDxseMdYcCRqZ/btQk69YdLnodBn2+cuguUgltEstv/mOTt/Y6CnRtqnGSw39F+Rfea60+26QjnPQZXL4HvL/IDctqmGWizZUXtc3ULoOAWkbo45Xdw0CRo3x2GfglOvx0G1ViBcOiJcNE/YcBhma/TvqvvddJtMHznbZj449Rzlr7kF2mQjBTcIpJdh+5w1t/g6sXw5Rv9w8jqIezVWrWPv9++Du47C37aww+VX7cw9Zpt94Wjr/BdCxNtWwOPf6PRf4VCouAWkbqbcR3cPBL+eDgseDL52AfT4++nXw2LnvGjJVfOhkcvTn89Myhum7p/7sN+9XdJS8EtIulVVsDMn8Mfj4SHzvOL+b5+a7z/NjUG7yWuE7n8teRj6xbArs3pv+ewSzN8f4YJrUTBLSIZvHKTf1C4bj4s/Ac8fVXmc1t3ghMThqj3G598vNuwzCvBH3sdtK+xzmSPEdB9WIPKbg40clJE0vvwX8nb29f6UZMVu5P3t+4IVy1I7tt90g1+YqqlL0Gvg/1akulsXg53nQQ71ibvb9tp7+svYApuEUmv2zA/P0m1Fq1gn15+Vr9EZVv9vNuJwd2xt19YYdsa6D0m84rws37juwDW1KbzXhZf2BTcIpLehOth7Vw/YrL6TrtmaAO0bOe7CVbbvALuP8u3awMUt4NjroY2+8DwU3z4J55bU1EbP9ugZKQ2bhFJtW2tXzxh34Fwwk99OGdy9JXwyTsw+y+w8SP426nx0Aao2An//glM/z78YTysSxgOP/L05Gu17wHfnQP9a7SRSxJN6yoiyaqq/ERS69P0vU6n6xDYuMi/b1EEVWmmaE007iI45eb49tv3+rm+O/f3d+aJvVNE07qKSB2sebfuoQ3x0IZYaBspXQUT1Vy38pDz/UvqTE0lIpKsfQ8y3OjVTcc+mY9ZMZRc0vBrC6DgFpGaOvWFz+3Fw8FuQzMfm/xn6HtIw68tgIJbRNKZ+CM48y5o27X+n132WuZjW1c2vCb5jIJbRNIbeTpM+J/6fcZaQOXuzMerF2Ooaeen8MhF8OsD4N7JmqckCwW3iGS2bU39zq85019NvUfDnAdSF2b45/dg/jTYudEvNPzHI+Dxb8K8adl7qTRDCm4RyWzEZGjRMvt51WouoADQsr3v4jdqCrzwf/DEN+HPx8BLv46f8/HLyZ+p2A3vPgCPXqQpXtNQcItIZt2G+tXd66qyws9dUq1Tf7hyHlwRG4GZ2BXw5Rth5yZY/gb0OCjzNec+Gl98WAD14xaRTCor4OkrYcXrmc/p2Be2JoRq2ZZ4cPcZC+c85Bf/nTfNzzKYqGK3H+iz7ROgBbTp5NeyTMf2ontiAVJwi0iqPbv8yjVr0zxMHPJFOPJyf05VJTw4Jfl42Vb/85N34Jnr4Mw7YdaNqdfp0DsW2gBV/noUATXatIefUnvf8GZITSUikurZH6YP7RYt4YSf+GXHzGC/I/x8Jpl88o7/uTVNU0eHHsnbleWkhHZRa98tUZLojltEUn04I/3+qj1w2+fibdUtWsKI02H4qbBrk+8RkhjSLdvB38+M34UnGn6KH15fmx7DoUgxVZPuuEUkVW2jHxMfMFbtgbkP+fbqSX+Acx+Bfof6/tzg79oXPweuxp107zFw2DfAimqv4/BvNaj8QqfgFpFUJ/4CuhxQ9/MXPu1/9hwBo6ckrEuZxv7HwjkPAC7zQ8cOPeGkG/21JIWCW0RSdR8Gl78N+x1Vt/PbdIwv7vv+07Wfu2mJf9jYppNvZkln+1qY/j0/CEdSKLhFJFX5TvjLBFj2at3OX/++H6r+yRzfzl2bLatgRSncfDDMfRiwzE0m7z4AK2bXp/JmQa3+IpLqjdvgk7fr95mPX878UDORq4I7JybuiLeBtyiGqork87d+giTTHbeIpFo7P/3+4ra1f66q0q9PWataFlnoPICkucDbdYPBEzOe3lwpuEUkVbtuqfvadoFLnq3loaXBrF/7HiYN1aYTDP0i9BoNY8+Hi59JP/9JM6emEhFJtfHD1H0XTff9qnsclGHa1b1cv9aK4gN2ALoN9i9JoTtuEUmVsqq7QasO/m2X/XPznUWtkrfnTfPzdEsKBbeIpDroNJLamgcd51dhBzjqCj+vdjbWws9HAj6U+42vXw3FrVPDXAAFt4ikM+fvJDV9LJ0Fq+f59+27wTdmwbff8NO2ptNrFFzwJHz/fbjwaZjyAJzzMAyq5UFjxa7k7W5DYO4jsGcv2swLlIJbRFJtWJy8XVUB02Krs7/5V7jzi/Dcj2DU2ek/P24q9BgBT14G95wM950Bd58Ep98OXYbU/t2tYg8j18yFp6+A+8/am9+kIJlze/lAIQ9KSkpcaWlp1GWINB/Tr4bZt6fu73NIcv/uotZQWZZ63n5HpR+80/8wWPFG/eu5rNTfgTc/aecEUK+SJmzd1t3c9erHfLR+O2eN78fxw3sBsHX3HorMaN86+X++e1//mPdWbuHQgV04/ZB+FLVIPw/E3JVbmLtyM1t27+G4YT0Y0LUdt85czJwVmzl0YFe+eewBtC7OMvmPFLYTfuqHrtcc/FJzUE660G61T+YRlw0JbYCieiyf1gwouJuosopKJt36Kqu3+Pa9Zxes5bzDB7CjrJIn56yihRmnj+1LFbDi0518uHYbm3b6uSIeKV3JO8s3M+HAHmCO22ctZe7KLRzYqwMrN+1i/fbyz77nVzM+oKiFUVnl/+X16uKNrN22m59PPjjvv7M0IS3bQP9DYf4T9fxce+jYCzZsy3JiCyDNRFS9x8KGD2DPzvi+QRNrn/O7GVJwN1H/Wbzxs9Cu9vfXl3/2vso5Hn5rZcbP3z97OffPXp60750V6ZeFqg7tao+/vYpJo/tw2AFd61u2FJKGNKMe8Hm/dNmGRbWf96Vf+qld+4zxc3qXbfGTVHXoAWvmwcyfw6aPYcRpcMzV9a+jwCm4m6iWxdGtsbdrTyVn3/46PfZpzZCeHbjuS8MZ0bdTZPVIRA6/DBY8Wb/P9BgOh3/b98Guiv/LjjadYfdm/77bMBh7HrRqHz/edt/4+14j4Zz7G1p1sxBJrxIzO9HMPjCzxWZ2TRQ1NHUzF66LugTWbSvj1cUb+fLvX2Huys1RlyP5NuBQOOFn8blHWnfyk0B1PxA+932YdKsf/l69aMKAI/1alO27wYVP+e2ug2HC9fCdOXDq7+G02+DSmcmhLfWW914lZlYEfAicAKwE3gTOcc4tyPSZ5tirZPC1/6SiCXX4KTZY/IsvR12GRKF8J5TvgA7d0x/fvcW/Og/Ib13NQ5PpVXIosNg5twTAzB4EJgEZg7s5akqhDU2vHsmjVu38K5M2nfxL8iaKppK+wIqE7ZWxfUnM7FIzKzWz0vXr1+etOBGRpq7Jjpx0zt3unCtxzpV0757hn2gFbL8uWeY9zrNB3Wq54xKRvIoiuFcBiRMc9IvtkwQv/fcERvZuGvMQHzOkK89/79ioyxCRmCjauN8EhpjZ/vjAngJ8NYI6mrynv3tM1CWISBOU9+B2zlWY2WXAM0AR8FfnXIZ1kkREpKZIBuA456YD06P4bhGR0DXZh5MiIpKegltEJDAKbhGRwCi4RUQCo+AWEQmMgltEJDAKbhGRwCi4RUQCo+AWEQlM3hdSaAgzWw8si7qOgHUDNkRdhDRL+rO3dzY4506suTOI4Ja9Y2alzrmSqOuQ5kd/9nJDTSUiIoFRcIuIBEbB3TzcHnUB0mzpz14OqI1bRCQwuuMWEQmMgltEJDAKbqmVmX1sZt2irkPCYGZTzaxPwvaLZlYSez/dzDpHVlwBUXAXMDOLZGk6adamAn3SHXDOneSc21zXC5lZUSPVVHAU3E2cmQ00s4Vm9hczm29mz5pZWzMbY2avm9l7Zva4me0bO/9FM7vZzEqB78a2bzKz0th1xpvZNDNbZGY/S/ieJ8zsrdh3XBrZLyxNjpldZWbzYq8rYn8m5yUc/76Z/djMzgRKgPvMbI6Zta1xnc/+9WZm55nZ7Nh5f64OaTPbbmY3mtm7wBF5/DWDouAOwxDgVufcCGAzcAbwN+AHzrlRwFzgfxPOb+WcK3HO3RjbLo+NXrsNeBL4L2AkMNXMusbOudg5Nw7/f7zvJOyXZszMxgEXAYcBhwNfB/ZNd65z7lGgFDjXOTfGObcrwzWHA2cDRznnxgCVwLmxw+2BN5xzo51zrzTm71JI9E/pMCx1zs2JvX8LGAR0ds69FNt3D/BIwvkP1fj8U7Gfc4H5zrnVAGa2BOgPbMSH9eTYef3xf1lsbMxfQoJ0NPC4c24HgJlNAz63l9ecCIwD3jQzgLbAutixSuCxvbx+wVNwh6Es4X0l0DnL+TsyfL6qxrWqgGIzOxY4HjjCObfTzF4E2jSwVil8nUn+13p9/6wYcI9z7to0x3Y75yobWlhzoaaSMG0BNplZ9Z3P+cBLtZyfTSdgUyy0D8T/k1gE4GXgNDNrZ2btgcnAv4AeZtbVzFoDJyecvw3YJ8s1XwDONLMeAGbWxcz2y0HtBUt33OG6ELjNzNoBS/DtkA01A/immS0EPgBeb4T6pAA45942s7uB2bFddzjn3jSz/4vtWwW8n/CRu/F/LneR4eGic26BmV0PPGtmLYA9+Ocumrq5jjTkXUQkMGoqEREJjIJbRCQwCm4RkcAouEVEAqPgFhEJjIJbRCQwCm4Jgpn1MrMHzeyj2GRY081sqJntik1UtMDM/mZmLWPnH2tmT8feTzUzZ2bHJ1zvtNi+M2v5zlaxCbsWxybletLM+tWhVk1tKjml4JYmz/yEFo8DLzrnBsUmw7oW6Al8FJuo6GCgH3BWhsvMBaYkbJ8DvJvlq3+OHwU4zDk3BHgCmBarpzZT0dSmkkMKbgnBccAe59xt1Tucc+8CKxK2K/Ej+fpmuMbLwKFm1tLMOgCDgTmZvjA2IvUi4MrquTOcc3fh53qZoKlNJUoKbgnBSPysiBmZWRv81KMzMpzigOeBLwKTiM+YmMlgYLlzbmuN/aXAiEwf0tSmkg8KbgndIDObA6wFVjvn3qvl3AfxzSVTgAfyUFttEqc2nRPbPiB2TFObSq0U3BKC+fiQS6e6jXsQMM7MTs10EefcbHxbeDfn3IdZvvMjYICZ1ZzpblysngoaZ2rTMbHXMOfcj2PHNLWp1ErBLSH4N9A6cUk1MxuFX/ABAOfcBuAa/EPL2lwDXJftC2MLB9wD/Dah7fkCoF2snrVoalOJiIJbmjznp7CcDBwf6w44H/gFsKbGqU8A7RLmKU93rX8552bW8auvBXYDH5rZIuArwGTn7QGqpzZ9jvRTm6Y8nEyoYwFQPbXpe7Fr9K5jXdLMaVpXEZHA6I5bRCQwWgFHmj0zexzYv8buHzjnnomiHpFs1FQiIhIYNZWIiARGwS0iEhgFt4hIYBTcIiKB+f+FdsTg6E62+AAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"col_x= \"CRIM\"\n",
"col_z = \"{}_Z\".format(col_x)\n",
"col_outlier = \"{}_Outlier\".format(col_x)\n",
"df_x = pd.DataFrame(df_xs[col_x])\n",
"median = np.median(df_x.values)\n",
"median_abs_std = np.median([np.abs(v - median) for v in df_x.values])\n",
"print(\"median={}, median_abs_std={}\".format(median, median_abs_std))\n",
"\n",
"threshold = 3.5\n",
"df_x[col_z] = 0.6745 * (df_x - median) / median_abs_std\n",
"df_x[col_outlier] = np.where(np.abs(df_x[col_z]) <= threshold, 'normal', 'outlier')\n",
"print(df_x.head())\n",
"\n",
"sns.catplot(x=col_outlier, y=col_x, data=df_x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Tukey Outlier\n",
"\n",
"Modified Z-score 방식과 같이 Skew 된 데이터에 대해서 강건하도록 Median 값을 이용하는 다른 이상치 탐지 방법입니다.\n",
"\n",
"Boxplot에서는 이상치(Outlier)에 민감하지 않은 분위수를 사용하기 때문에 이를 이용하여 통계적으로 이상치를 잘 검출할 수 있습니다. Boxplot 에서 이상치는 통계적 최소값인 Q1 - 1.5 x IQR 보다 작거나 최대값인 Q3 + 1.5 x IQR 보다 큰 값들을 가르킵니다. \n",
"\n",
"* IQR(interquartile range) = 3rd Quartile - 1st Quartile\n",
"* Upper Bound = 3rd Quartile + (IQR * 1.5)\n",
"* Lower Bound = 1st Quartile - (IQR * 1.5)\n",
"\n",
"질적변수에 속하는 명목척도, 서열척도의 경우 평균을 구할 수 없기 때문에 사분위수를 통한 데이터 탐색은 더욱 의미가 큽니다."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"q1=0.08204499999999999, q3=3.6770825, lower=-5.31051125, uppwer=9.06963875\n"
]
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAFvCAYAAABq/iEqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAl4ElEQVR4nO3deXhV1b3/8fc3A5CEIQxhBpkVrAwScACrFWot+hO1jrV11tprW6u316Fz77W919Zeq50sYiu2Xq3igFbFAQVFBQmzzJNMMoQpTIGQZP3+2CdmOsk5JDnZZyWf1/Pk4ex19tn7eyz9sLL23muZcw4REfFHStgFiIjI8VFwi4h4RsEtIuIZBbeIiGcU3CIinkkLu4B4nH/++W769OlhlyEi0tgsWqMXPe5du3aFXYKISNLwIrhFRKScgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhGJ39YFsPApKNgSdiXNmheTTIlIEnj3VzDrgeB1agu4+hkYMC7cmpop9bhFJLajB2D278q3S4pg1q9DK6e5U3CLSGzFRUFYV1R0MJxaRMEtInHI6ggnX1y5bdRNoZQiGuMWkXhdMgn6nAU7V8DA82DQeWFX1GwpuEUkPmkt1MtOEhoqERHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCQ1uM7vTzJaZ2Sdm9rSZtTKzvmY218zWmtk/zaxFImsQEWlqEhbcZtYD+B6Q65z7ApAKXAU8ADzknBsA7AVuSlQNIiJNUaKHStKADDNLAzKBbcC5wNTI+1OAixNcg4hIk5Kw4HbObQUeBDYRBHYBMB/Y55wrjuy2BeiRqBpERJqiRA6VtAcmAn2B7kAWcP5xfP5WM8szs7z8/PwEVSki4p9EDpWMBzY45/Kdc8eAF4AxQHZk6ASgJ7A12oedc5Occ7nOudycnJwEliki4pdEBvcm4HQzyzQzA8YBy4F3gcsi+1wHTEtgDSIiTU4ix7jnElyEXAAsjZxrEnAPcJeZrQU6Ao8nqgYRkabInHNh1xBTbm6uy8vLC7sMEZHGZtEa9eSkiIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhn0mLvIiISsfJV+OR5aNcTzvgutNYiJ2FQcItIfD55AabeUL695i247QNI0S/ujU3/xUUkPoufrry9czlsWxhOLc2cgltE4pNVdVjEILNTKKU0dwpuEYnP2LugdZfy7TNuh/YnhFdPM6YxbhGJT6cBcMdi+PSD4OJk55PCrqjZUnCLSPzSM2Dg+LCraPY0VCIi4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLSPI4sAM2zYXiorArSWqaZEpEksPHj8H0+6D0GLTpBt98EToPDruqpKQet4iE78h+ePMnQWgDHNgG79wfbk1JTMEtIuE7vBuKCyu3FWwJpxYPKLhFJHwd+kL3EZXbvvC1cGrxgMa4RSQ5fP1ZeO9B2L0GTpwAo24Ou6KkpeAWkeTQujNM+HXYVXhBQyUiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLiGQW3iIhnFNwiIp5RcIuIeEbBLSLimYQGt5llm9lUM1tpZivM7Awz62Bmb5nZmsif7RNZg4hIU5PoHvfDwHTn3EnAMGAFcC8wwzk3EJgR2RYRkTglLLjNrB3wReBxAOdckXNuHzARmBLZbQpwcaJqEBFpihLZ4+4L5AN/M7OFZjbZzLKALs65bZF9tgNdon3YzG41szwzy8vPz09gmSIifklkcKcBpwJ/ds6NAA5RZVjEOecAF+3DzrlJzrlc51xuTk5OAssUEfFLIoN7C7DFOTc3sj2VIMh3mFk3gMifOxNYg4hIk5Ow4HbObQc2m9mJkaZxwHLgZeC6SNt1wLRE1SAi0hSlJfj43wWeMrMWwHrgBoJ/LJ41s5uAjcAVCa5BRKRJSWhwO+cWAblR3hqXyPOKiDRlenJSRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRMQzCm4REc8ouEVEPKPgFhHxjIJbRBpG4T4o3Bt2Fc1CQld5F5FmwDmYfi/Mmxy8HnENXPgwpKhfmCj6Lysi9bN2Bsx9FEqLwZXAgidhxbSwq2rSFNwiUj/5K6q37YzSJg1GwS0i9dP/XLCKUWIwYHxo5TQHCm4RqZ8uJ8PlU6DHSOg2HC59DHqNDruqJk0XJ0Wk/oZcFPxIo1CPW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEMwpuERHPKLhFRDyj4BYR8YyCW0TEM7U+OWlml9b2vnPuhYYtR0REYon1yPtUYFHkB8AqvOcABbeISCOLFdyXAlcBQ4FpwNPOubUJr0pEmp4dy2DTR9BzNHQbGnY1Xqs1uJ1zLwEvmVkWMBH4rZl1BH7knJvVCPWJSFMw/wl45Y7y7QkPwuhbQivHd/FenDwCFAD7gdZAq4RVJCJNz8wHqmz/Tzh1NBGxLk6eSzBUMhp4G3jYOZfXGIWJSBNSXFhl+2g4dTQRsXrcbxOE9mygJXCtmT1S9pPw6kSkaRj9rSrbGiapj1gXJ28kuHtERKTuvnRfsFLOpjnQaxQMuTjsirxmziV/Lufm5rq8PI3QiEizY9EaY41xv0ItPW7nnNYqEhFpZLGGSh5slCpERCRuse7jrvFebTMb0/DliIhILLGGSlKBK4AewHTn3CdmdiHwQyADGJH4EkVEpKJYQyWPA72Aj4FHzOwzIBe4N/JUpYiINLJYwZ0LDHXOlZpZK2A70N85tzvxpYmISDSxHsApcs6VAjjnjgDrFdoiIuGK1eM+ycyWRF4b0L/CNs45TfEl0lStfgPWz4Sup8DQKyElNeyKJCJWcA8DugCbq7T3Ihg2EZGmaO5f4PW7y7c3zYGLNMtFsog1VPIQUOCc21jxh2CmwIcSX56IhGLuXypvL3oKig6FU4tUEyu4uzjnllZtjLT1SUhFIhK+9MzK26ktISXWL+jSWGIFd3Yt72U0YB0ikkzOvhuswpj2WXdCWsvw6pFKYv0TmmdmtzjnHqvYaGY3A/PjOUHkIZ48YKtz7kIz6ws8A3SMHOObzrmi4y9dRBJmyEXwnXmw4T3oOhR6jgy7IqkgVnB/H3jRzK6hPKhzgRbAJXGe4w5gBdA2sv0A8JBz7hkzexS4Cfjz8RQtIo2gY//gR5JOrUMlzrkdzrkzgV8An0Z+fuGcO8M5F/OuEjPrCVwATI5sG3AuwerxAFOAi+tYu4hIsxTX1Qbn3LvAu3U4/u+Au4E2ke2OwD7nXHFkewvBPCjVmNmtwK0AvXv3rsOpRUSapngXCz5ukcmodjrn4hoLr8o5N8k5l+ucy83JyWng6kRE/JXI+3vGABeZ2QSCVeHbAg8D2WaWFul19wS2JrAGEWloh3aDGWR2CLuSZithPW7n3H3OuZ7OuT4EK8W/45y7hmDI5bLIbtcB0xJVg4g0oNJSmHY7PDgAfjMA/nUneLD0YVOUsOCuxT3AXWa2lmDM+/EQahCR47XiZVj4D3Cl4Eog76/BfCbS6BrlUSjn3ExgZuT1emB0Y5xXRBpQ/qoobSvhxPMb5vh7NsCbP4ady2HgeTD+55Cu5/yiCaPHLSI+GjieSouOWwoM/HLDHf+Za2Dlv2DPepj7KLz9i4Y7dhOj4BaR+PQYCZf/DXrkQs/RcMXfocvJDXPsgq2wc1nltrVvNcyxmyDNGiMi8Tv5kuCnobXuDFk5cCi/vK3zkIY/TxOhHreIhC81HSb+CbI6B9tdT4Hz7g+3piSmHreIJIdB58Fdy+HwbmjTNexqkpp63CKSPFLTFdpxUHCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS0i4hkFt4jEr7QUNn4EW+aHXUmzlhZ2ASLiiaMHYcr/g88WBNv9x8HXn4VUxUhjU49bROKz+Ony0AZYNwNWTw+vnmZMwS0i8Tm4I0rb9savQxTcIhKnL3wNUluUb7dsCyddGF49zZgGp0QkPp0Hw/WvQd7jkJoOp30b2nQNu6pmScEtIvHrNSr4kVBpqERExDMKbhERzyi4RaTxFe6FpVPh0w/CrsRLGuMWkca1cyX89StwZF+wPfRKuHRSqCX5Rj1uEWlcH/6+PLQBlvwT8leFVo6P1OMWkeNXdAhWvAKlJTDkImjZJv7PHt0fpe1Aw9XWDCi4RSR+O1fC3Edh2YvlveZZD8CtMyGzQ3zHGHk9rPwXuNJgu+tQ6DEyAcU2XQpuEYnPvk0weTwUVekd79sIS56F028D52DTHEhJq/l+7wHjggd5Pnke2naH3BvBLPH1NyEKbhGJzycvVA/tMiVHg+GTKRfB1rygre/Z8I3ng6csqzrhjOBH6kQXJ0UkPhnto7dndoRTrgguMpaFNsCGWcGQiDQ4BbeIxOeUy4Lx6DJtu8PZ98Jts6FtNzi4s/pnDubXfsz81fD01+GPp8M790NJccPW3ERpqERE4tMiC255FzbMBAz6nQMpqeXvn3wpvP+/wbAJQIs2MLiW2QNLS+Cpy4IxcoD8FZDaEs7+jwR9gaZDwS0i8UtNgwHjo7+XMwhufB3mPR4E+mm3Bb3ymuSvKg/tMqunK7jjoOAWkYbTY2T8t/a16wlpmVB8uLyt80mJqauJ0Ri3iITDlUCr1uXbaRkw9gfh1eMR9bhFJByLn6l8QbO4EN7+aTC8MvRK6HFqeLUlOQW3iISj6FD1thUvB3/Omww3vA69RjduTZ7QUImIhGPoFdCyXfT3SothwZONW49HFNwiEo7s3vCtmTD2Lhh+TfX3j2fiqmZGQyUiEp4O/WD8z4LXh3cHtwNC8DTmad8Kr64kpx63iCSHSydD5yHB68O7YfZD4daTxBIW3GbWy8zeNbPlZrbMzO6ItHcws7fMbE3kzxomQBCRpHJod/TH2hvKgidg5/Ly7flPwMaPEnc+jyWyx10M/LtzbghwOnC7mQ0B7gVmOOcGAjMi2yKSrJyDV38ADw6EBwfB8zcnZk6RfZuitG2s3iaJC27n3Dbn3ILI6wPACqAHMBGYEtltCnBxomoQkQaw7h2Y91jwwAwOlj4XzKVdZs8GmPFf8M4vYd/mup9nyESgwrzcLdrU/Hh9M9coFyfNrA8wApgLdHHObYu8tR3o0hg1iEgd7VodpS2yRmTBVph0TvlqOHl/hX+bA61zjv88fcbCVU8Fx2jRGsbeCVmd6lp1k5bw4Daz1sDzwPedc/utwkoXzjlnZq6Gz90K3ArQu3fvRJcpIjUZMD5Y0aa0bHjEYND5wculz1Ve+PfwrmBZs9Nurdu5Trog+JFaJfSuEjNLJwjtp5xzL0Sad5hZt8j73YCoVzucc5Occ7nOudycnDr86y0iDaPTQLj6GThhDPQcDZc9Xv5EY4us6vvP+AU8PLzycIo0KHMuaoe3/gcOutZTgD3Oue9XaP8NsNs59z9mdi/QwTl3d23Hys3NdXl5ebXtIiJhOFIAj42D3Wuqv2cp0L4vHCsMFgg++26tLXn8ov4HS2RwjwXeB5YCkeWc+SHBOPezQG9gI3CFc25PbcdScIsksWOFwYMzeX8LliuryaWPBY+5A+xcEUwy1aodnHodZHVsnFr9EzW4EzbG7ZybXdNJgXGJOq+INLL0DDj5Ejiyv/bg3vBeENzblwarxRcfCdoX/j24oJnWMhhe+fD3gMGYO+DkixvjG3hHj7yLSMMY8Q3Y8UkwOVR6JhRW+UW6+4jgzwV/Lw9tgD3rYe3b0KYbTL0JiIwCTL0heCS+21CkMj3yLiINIyUVJvwGfrgN7tkAEx6EVtmQkh4Mh5x6XbBfekb1z6ZnBuFNhaFbVxppk6rU4xaRhpUS6Q+OvgVybwwWBU5rUf7+qJth8dNwcEew3XUoFGyG1lEe6Sibu0QqUXCLSOKkpFZeCR4guxd8Zx6sej2453v1dHj5u8HSZSdOgNVvBHefjLwBBn0lnLqTnIJbRBpfq3bQ/1x46dvlbcWFUHIM7l4HGGRkh1Vd0lNwi0jj270ONswOxrErKjoEGZowNBYFt4jU38aP4Oh+6HdOcFtfbT54BN76KcGFyBTKH/MA0lolrsYmRMEtInXnHDx9VfnKNe37wE1vBUMhq98I2gZ9pTzMjx6Ed39F+d0jVXrc69+BbUuh2ymNULy/FNwiUnefvl8e2gB7P4WP/gRr3ihfFKHjIDj1m1BSBP2+FIxl1+YvY6HXaXDppOAfAqlG93GLSN0V7q3etjWv8ko2u1fDWz+Bd/4LnpwIvc+MfdzNc+FfdzZcnU2MetwiUrNVr8OaN4P7qU+9Nhjy2P5JMMVr9+HBlK9tusGByBT7KWnQ9ZSgJx5N0YHg4mPvM4ILk7k3Bqu5L/wHrHqt8r5b5yf0q/lMwS0i0c17HF69q3x7w3vBcEfZ0Eifs+CaqXDz2zD3L8FMgadeC+16BvOPHD0Q/birXi1/3W049MwNFmtIbREcv8wJYxv8KzUVCZsdsCFpdkCREPx5TDD3yOeMSo+kA1z0+yCsq3p0bDCZVFWWUvkWwJR0KD1WeZ/UFsFj8Vld4Mzbgylhm6+oE/VpjFtEomvZpvJ21ScgAfZ/Vr1t8TPRQ/vM70HrrpXbos3PXXIs6L3vXg2v3AHrZ8ZdcnOh4BaR6M6+B1Ir3JM96pZgMqgyKemRBX4rOLwnCNto0jPhQJWgrzg08rkqvfq1M+IuubnQGLeIRNf/S3DHIlg/CzoPDi5GDr0c5vw5uDg5+tagvaI96ytP2Vqmw8DaZ/pLSQNLDdayXDGt8ntdTq7vN2lyFNwiUrO23WH41eXbPUbC1ybXvH+rdtHbD2ypPENgVVld4PuLITUdZvwnfPiH4B+HYVfDKZfXrfYmTMEtIrUrPhrcFlhaHMze1yKz5n33fhq9/VhhcMtgaisoidIj739OENoA434KY+8KzqeJpqJScItIzYoOw+NfLr+7pEM/uOWd8omgSo7BBw8HFxC7DYPTboOW7eBoQfVjFe6F7y6AzXOCu0bmTwmO239cMJ6+8B/BXCUnXQgtWzfaV/SRgltEarZ8WuVbAvesh8X/hNNvC7bf/jl89Ifg9afvQ/4q+Mbz8O79sG1J5eXLBp0PHfsFPwA5J0HLtjBvMjwyvPw2wa6nwM0zYk9W1YwpuEWkZscOR2k7VP562UuV31v7Flz+N7h2GhQXBb3xDbOCC5tf/I9gnyMF8NTlwWPt0WxfGgzNaKHgGul2QBGp2ZCLIatz+XardjD0yvLt7F6V97dUmPsYrHkL/n5x8JTlyOvhvPvLL1x+/FjNoV0m6m2CUkY9bhGpWVZHuHUmLJgCmz6Co4dg9kNw9r3QOicI5P+7Ag7vDvZ3JfDOLyo/Ifn8TdCme3BRM7NDzRcwy7TuElwElRopuEWkdu16BPNub3gv2P5sfjDR1E1vBPOMnHMfvPaDyp+purLNc9fCoXzAgouPFaW2hNQ0KC2FfmfDxD/q4mQMCm4RiW35S5W3N8+BLfOC0G3XK+pHKjmUH3nhYOUrwURUEEwydfY90G1oAxbb9Cm4RaR2h3ZVn+kvtQVMHh+87pEL2X1g36cV3m8JJUeD1+16Q8Gmyp8v2BJ5rye8+eNgXpSz/h16nJqIb9DkKLhFpGZ7NsCfz6x8d4mlVr54uDUPxv0MsjoF92ZvzSsP7dad4bxfwnPfjH78TXPKX6+fBXcshl2rIO+vwT3dZ9xe/bF6UXCLSC1euaP6LYGZneDQjsptBZvhrLuC4K7o4E54/gbIzIHD+dSq6ABMHgf7NpaPkS9/Gb47P7gQKp/T7YAeKCg8xm/fXMW3/zGfqfO31LpvYVEJxSWlte4jErct86q3dexfZU4SC24bhODpyapKi2OHdpm9Gypf2DxaUHlNSwHU4056paWOS//0Aevyg4ceXv9kO/sLj/G1U3vSLjP98/2OHCvh7qlL+NeSz2iXkc59Xx3MFaNiXzR6d9VOHntvPaXOcctZ/Rg3uEvCvot4xrnoD+BM+E3w5+yH4Oj+4D7tfmcHbef+OHi6cv27DVdHm66x92lmtAJOkrt76mKezavcy26ZlsLR4lL652TxyNUjOLl7O/48cx0PTF/5+T4pBv9382kUHiuldas0RvXpUO3Yq3cc4KsPv09Jqfv8My/+2xiG9cpO6HcSj/xhdDDmXCZnMNw+p+b9y3zwSLBAcEV9zoKiQ/DZgsrtLdvUvMzZiRfAlf+AlGY7OBB1BRwFdxIrLCrmlF+8SXFJzf8bDenWlmnfGcPEP37A8s/217jfuJM6M/m6XKzCiiNVwx4gIz2VUX3bs2jTPrpnZ/DTC4dw5oBO9f8y4qfN8+C562H/FsjuDVc8Cd1HxP5caSk8PKz8bpLUlnDb+8EsgY9/ufziZst28K1Z8MaPgrUoLRVO+1Yw9JLeKvrQS/Oi4PZJaanjykkfMe/TvbXuZ8CoPu35OMZ+EPTAK4bwg2+s4g/vrq31M61bpDL3R+PJaqlRtWartCRYoqxtj+Pr+R47Etz/fXhPMO9I2+5B+2cLYeFTQU979C3l7QVbg4mlstRRqCBqcOv/jUlqzobdUUN7cLc2rNhW/mulg7hCG+C9Nbs4o39HzIydB44w6f31MT9zsKiE5dv2Rx1qkWYiJbX6nCTxSG8Fw66q3t59RPRee7sex3+OZkrBnaSKiqvfGXLRsO6MPCGbn728vE7HfHTWOrbuPczE4T04XFQc9RzRdMiqZeUSEWl0Cu4kNWZAJwZ1ac3qHQcBSEsx+nTM5NFZsXvJAJ3btGRUn/bMWp3PwaMln7e/smQbryzZRte2LTGqLctaTVqK0aVtqzp+CxFJhGZ7qTbZpaemMPXbZ3LjmD6kGBSXOh55Zy079kdZ9imKnQeO0i+nNV3bZUR9f/v+ozFDG4LzPvjGqtg7ikijUXAnsbat0lm6tYDSCglbWkPadmlbfbWQpVsLuO3s/nGfz4AWadX/Sjzx4aes3F7zHSsi0rgU3Elu057Cam1fH139QtHeQ0VkpKdWaju9bwcuG9mTabeP4c4vD6w0Vh3tUvWPLxhM+8zoo2fb9sXX0xeRxNMYd5Ib0q1NteGRC4Z257n5WzhW4f7uohIHJSWYBQ+8Afzv22tITTVuOas/w3plc0VuL6Z8uJGP1u1i+bb9lT4PgEH+georj2S1TOX0fh0b/LuJSN2ox53kfjhhMNkZ5Y+233hmH3712orqoRtR8bb8ouJSfvnqSv4yax0HjhyjW7sMerXPYPGWgmqf75DVgv95fWXUoZgfTRhMRovU6m+ISCj0AI4HDh0t5qN1u+nZIYP+Oa0Z+KPXj/sYmS1S+fXXhvLwjDWs2Xmw0nupBt3aZbBlX/VhmatG9eK/Lz2l0hOXItJo9ACObwqLSvjdjNXMXb+Hfp0yGdilLZ/tK2R4r2wWbd53XMc6XFTCd55eSMco92SXOKKGduuWqYzq00GhLZJk1ONOYvdMXcI/8zZXax8/uDP5B46yZEtBjbf0pabY55NH1UeKwTv/fg59OmXV+1gictyi9po0xp3Epi/bHrX97RU7WVxLaJ83pAur/ut8vjKk/lO0ljpYuDm+R+pFpHEouJNY7w7RH56JZdlnBVz4+9l0y27FZafWb/6HFIMRvdrX6xgi0rAU3EnsxxcMqdPntu47wsrtB3jiw41ktEhj8rW5nNi1zXEfJys9hV9fNkzDJCJJRsGdxE7r15EbxvSp1zFmrNjB+CFdGNu/5vuwv312f340ofqCrEdLHROHd6/X+UWk4Sm4k5Rzjsnvr2fx5n2k1uOmjv6dWzNz1U4e/+DTGvc5vX9HJgztVq29uMTxxrJtdT+5iCSEgjtJPT57A/e/uoIFm/ZRywI41aSnGm1aBXd59u6QyU8uHFJp/u6qRvftwNgBnchMTyWndfX5Tr7zf4sY/cu3OXDk2HF/BxFJDAV3knqjhjtKalI2N9SxEkf/nCxe/e5YZv7gHAZ1acNZAztR9VbsEzpkcFrfDvzkgiH8c95mTvvVDPIPHiU91Uipsu/OA0f51Wsr6vFtRKQhKbiTVJc2xzcHdsU1ERZtLmD22l2kRBL4Cz3a8bsrh3NS1zZ0aRP0qjfuKWTuhj1c/dgc/vOVZRSVBAc4VuKiPvY+/ZPj+4dERBJHwZ2kTu1Tv1vwtlZ5EnLi8B48e9sZ7D1ceRKpg0eLORLHSjiHjxbXqx4RaTgK7iQ1old2nT9rBhNOqX6x8cO1u4NZBKtolxF75oO2mekx9xGRxqG5SpLUiN7tuWpUL56ZV/2R91iG98xmcNe2OOd4fsFWPli7i5O7tyVv455q+6anGgWFsXvTPbLr9jCQiDQ8BXcSG3dS5zoF98LN+/jqw+9x8Yge/GnmOgBeXLg16r41TQ9b1bCe2cddh4gkhoZKkthdzy6q82c/KzjyeWg3hO+NG9hgxxKR+gkluM3sfDNbZWZrzezeMGpIdrNW7eRAhdXZw5SVbnSMco+3iISj0YPbzFKBPwJfBYYAV5tZ3SblaMIemL4y7BI+d+iY46E3k6cekeYujB73aGCtc269c64IeAaYGEIdSW15LU87huGx2Z+GXYKIRIQR3D2AilfctkTaKjGzW80sz8zy8vPzG604ia6N1pwUSRpJe3HSOTfJOZfrnMvNyckJu5xGN7Z/h7BLqOQ3VwwLuwQRiQgjuLcCvSps94y0SQX/uOUMvjig5qlYG0uawcu3j+GLgzqHXYqIRIRxH/c8YKCZ9SUI7KuAr4dQR9J78ubTwy5BRJJQowe3c67YzL4DvAGkAn91zi1r7DpERHwVypOTzrnXgNfCOLeIiO+S9uKkiIhEp+AWEfGMgltExDMKbhERzyi4RUQ8o+AWEfGMgltExDMKbhERzyi4RUQ8Y87Ft+ZgmMwsH9gYdh0e6wTsCrsIaZb0d69+djnnzq/a6EVwS/2YWZ5zLjfsOqT50d+9xNBQiYiIZxTcIiKeUXA3D5PCLkCaLf3dSwCNcYuIeEY9bhERzyi4RUQ8o+CWWpnZp2bWKew6xA9mdr2Zda+wPdPMciOvXzOz7NCKa0IU3E2YmYWyNJ00a9cD3aO94Zyb4JzbF++BzCy1gWpqchTcSc7M+pjZCjN7zMyWmdmbZpZhZsPNbI6ZLTGzF82sfWT/mWb2OzPLA+6IbD9kZnmR44wysxfMbI2Z3V/hPC+Z2fzIOW4N7QtL0jGzu8zsk8jP9yN/Jz+p8P4PzOznZnYZkAs8ZWaLzCyjynE+/+3NzL5hZh9H9vtLWUib2UEz+62ZLQbOaMSv6RUFtx8GAn90zp0M7AO+BjwJ3OOcGwosBX5WYf8Wzrlc59xvI9tFkafXHgWmAbcDXwCuN7OOkX1udM6NJPg/3vcqtEszZmYjgRuA04DTgVuA9tH2dc5NBfKAa5xzw51zhTUcczBwJTDGOTccKAGuibydBcx1zg1zzs1uyO/SlOhXaT9scM4tiryeD/QHsp1zsyJtU4DnKuz/zyqffzny51JgmXNuG4CZrQd6AbsJwvqSyH69CP6x2N2QX0K8NBZ40Tl3CMDMXgDOqucxxwEjgXlmBpAB7Iy8VwI8X8/jN3kKbj8crfC6BMiOsf+hGj5fWuVYpUCamZ0DjAfOcM4dNrOZQKs61ipNXzaVf1s/3r8rBkxxzt0X5b0jzrmSuhbWXGioxE8FwF4zK+v5fBOYVcv+sbQD9kZC+ySCX4lFAN4HLjazTDPLAi4BXgc6m1lHM2sJXFhh/wNAmxjHnAFcZmadAcysg5mdkIDamyz1uP11HfComWUC6wnGIetqOnCbma0AVgFzGqA+aQKccwvM7Ang40jTZOfcPDP7z0jbVmBlhY88QfD3spAaLi4655ab2Y+BN80sBThGcN1FUzfHSY+8i4h4RkMlIiKeUXCLiHhGwS0i4hkFt4iIZxTcIiKeUXCLiHhGwS1eMLOuZvaMma2LTIb1mpkNMrPCyERFy83sSTNLj+x/jpn9K/L6ejNzZja+wvEujrRdVss5W0Qm7FobmZRrmpn1jKNWTW0qCaXglqRnwYQWLwIznXP9I5Nh3Qd0AdZFJio6BegJXFHDYZYCV1XYvhpYHOPUvyJ4CvBE59xA4CXghUg9tbkeTW0qCaTgFh98CTjmnHu0rME5txjYXGG7hOBJvh41HON9YLSZpZtZa2AAsKimE0aeSL0BuLNs7gzn3N8I5no5V1ObSpgU3OKDLxDMilgjM2tFMPXo9Bp2ccDbwFeAiZTPmFiTAcAm59z+Ku15wMk1fUhTm0pjUHCL7/qb2SJgB7DNObekln2fIRguuQp4uhFqq03FqU0XRbb7Rd7T1KZSKwW3+GAZQchFUzbG3R8YaWYX1XQQ59zHBGPhnZxzq2Occx3Q28yqznQ3MlJPMQ0ztenwyM+JzrmfR97T1KZSKwW3+OAdoGXFJdXMbCjBgg8AOOd2AfcSXLSszb3AD2OdMLJwwBTgfyuMPV8LZEbq2YGmNpWQKLgl6blgCstLgPGR2wGXAf8NbK+y60tAZoV5yqMd63Xn3Ltxnvo+4Aiw2szWAJcDl7jAMaBsatO3iD61abWLkxXqWA6UTW26JHKMbnHWJc2cpnUVEfGMetwiIp7RCjjS7JnZi0DfKs33OOfeCKMekVg0VCIi4hkNlYiIeEbBLSLiGQW3iIhnFNwiIp75/99uX/bTg3wpAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"col_x= \"CRIM\"\n",
"col_outlier = \"{}_Outlier\".format(col_x)\n",
"df_x = pd.DataFrame(df_xs[col_x])\n",
"q1, q3 = np.percentile(df_x.values, [25, 75])\n",
"iqr = q3 - q1\n",
"upper = q3 + (iqr * 1.5)\n",
"lower = q1 - (iqr * 1.5)\n",
"\n",
"print(\"q1={}, q3={}, lower={}, uppwer={}\".format(q1, q3, lower, upper))\n",
"df_x[col_outlier] = np.where((df_x <= upper) & (df_x >= lower), 'normal', 'outlier')\n",
"\n",
"sns.catplot(x=col_outlier, y=col_x, data=df_x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
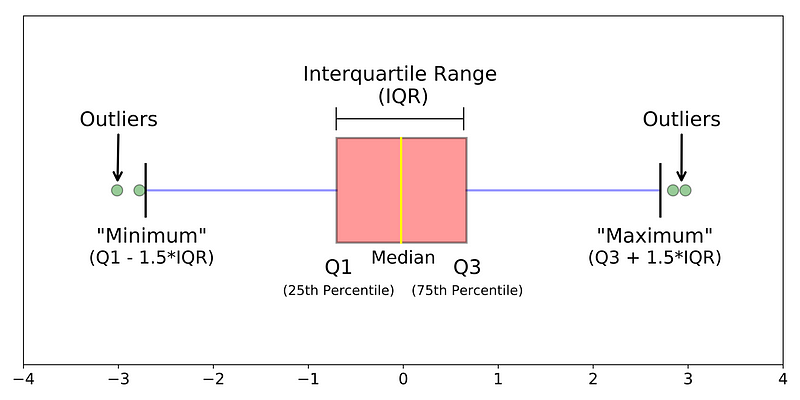
"보통 시각화 라이브러리들에서는 Tukey Outlier 방법을 boxplot 으로 제공하고 있어 한눈에 이상치가 포함된 데이터 인지 아닌지를 판단할수 있도록 시각화해줍니다.\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAD4CAYAAAD1jb0+AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAPi0lEQVR4nO3dbWydZ33H8e/fdrs+oK30xGqbFJZCaAGxB4bVMUFLSxzNYhPtJIQ6TcvZVMkS2ppuTBqFN7xB2pCmsQZNGxHddCIhHlTYWiHmYYciMgkVEigzbdgIXQo1STBnwKa1PBz7vxfnJCTBcc6JfXz7yv39vImv+9z2+UVKfrp0+VzXHZmJJKk8I1UHkCRdHAtckgplgUtSoSxwSSqUBS5JhRrbyDfbsmVLbt++fSPfUpKKd/jw4e9m5vi51ze0wLdv386hQ4c28i0lqXgR8cxK111CkaRCWeCSVCgLXJIKZYFLUqEscNVeu91mz549tNvtqqNIA7HAVXutVov5+Xn2799fdRRpIBa4aq3dbjMzM0NmMjMz4yxcRbHAVWutVovl5WUAlpaWnIWrKBa4am1ubo5OpwNAp9Nhdna24kRS/yxw1drk5CRjY90NyWNjY+zataviRFL/LHDVWrPZZGSk+99gdHSU3bt3V5xI6p8FrlprNBpMTU0REUxNTdFoNKqOJPVtQw+zkjajZrPJsWPHnH2rOBa4aq/RaLB3796qY0gDcwlFkgplgUtSoSxwSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCSVCgLXJIKZYFLUqEscEkqVF8FHhF/GhFPRsRXI+LDEXFFRNwUEY9HxNGI+GhEXD7ssJKkn7pggUfENmAPMJGZrwJGgXuA9wLvy8wdwPeAe4cZVJJ0tn6XUMaAKyNiDLgKOA68EXi493oLuHvd00mSzuuCBZ6ZC8BfAd+kW9w/AA4D38/MTu+2Z4FtK31/RExHxKGIOLS4uLg+qSVJfS2hvBC4C7gJ2ApcDUz1+waZuS8zJzJzYnx8/KKDSpLO1s8SyiTwX5m5mJk/AT4BvA64prekAnAjsDCkjJKkFfRT4N8EXhsRV0VEADuBp4DHgLf07mkCjwwnoiRpJf2sgT9O95eVXwLme9+zD3gH8PaIOAo0gIeGmFOSdI6+nomZme8G3n3O5aeBW9c9kSSpL+7ElKRCWeCSVCgLXJIKZYFLUqEscEkqlAWu2mu32+zZs4d2u111FGkgFrhqr9VqMT8/z/79+6uOIg3EAlettdttZmZmyExmZmachasoFrhqrdVqsby8DMDS0pKzcBXFAletzc3N0el0T0XudDrMzs5WnEjqnwWuWpucnGRsrHuixNjYGLt27ao4kdQ/C1y11mw2GRnp/jcYHR1l9+7dFSeS+meBq9YajQZTU1NEBFNTUzQajaojSX3r6zRC6VLWbDY5duyYs28VxwJX7TUaDfbu3Vt1DGlgLqFIUqEscEkqlAWu2vMsFJXKAlfteRaKSmWBq9Y8C0Uls8BVa56FopJZ4Ko1z0JRySxw1ZpnoahkFrhqzbNQVDILXLXmWSgqmVvpVXuehaJSWeCqPc9CUalcQpGkQlngklQoC1ySCmWBS1KhLHBJKpQFLkmFssAlqVAWuCQVqq8Cj4hrIuLhiPhaRByJiN+IiGsjYjYivt7784XDDitJ+ql+Z+APAjOZ+XLgV4AjwAPAgcx8GXCgN5YkbZALFnhE/AJwO/AQQGb+ODO/D9wFtHq3tYC7hxNRkrSSfmbgNwGLwD9GxJcj4oMRcTVwXWYe791zArhuWCElST+rnwIfA34N+LvMfDXwf5yzXJKZCeRK3xwR0xFxKCIOLS4urjWvJKmnnwJ/Fng2Mx/vjR+mW+gnI+IGgN6f31npmzNzX2ZOZObE+Pj4emSWJNFHgWfmCeBbEXFL79JO4CngUaDZu9YEHhlKQknSivo9D/w+4EMRcTnwNPCHdMv/YxFxL/AM8NbhRJQkraSvAs/MJ4CJFV7aua5pJEl9cyemJBXKApekQlngklQoC1ySCmWBS1KhLHBJKpQFLkmFssAlqVAWuCQVygKXpEJZ4Kq9drvNnj17aLfbVUeRBmKBq/ZarRbz8/Ps37+/6ijSQCxw1Vq73WZmZobMZGZmxlm4imKBq9ZarRbLy8sALC0tOQtXUSxw1drc3BydTgeATqfD7OxsxYmk/lngqrXJyUnGxrrH4o+NjbFr166KE0n9s8BVa81mk5GR7n+D0dFRdu/eXXEiqX8WuGqt0WgwNTVFRDA1NUWj0ag6ktS3fp+JKV2yms0mx44dc/at4ljgqr1Go8HevXurjiENzCUUSSqUBS5JhbLAVXuehaJSWeCqPc9CUakscNWaZ6GoZBa4as2zUFQyC1y15lkoKpkFrlrzLBSVzAJXrXkWikpmgavWPAtFJXMrvWrPs1BUKgtctedZKCqVSyiqPXdiqlQWuGrPnZgqlQWuWnMnpkpmgavW3ImpkvVd4BExGhFfjohP9sY3RcTjEXE0Ij4aEZcPL6Y0HO7EVMkGmYHfDxw5Y/xe4H2ZuQP4HnDvegaTNoI7MVWyvgo8Im4Efgv4YG8cwBuBh3u3tIC7h5BPGip3Yqpk/c7A/wb4c2C5N24A38/MTm/8LLBtpW+MiOmIOBQRhxYXF9eSVVp3jUaDO++8E4A77rjDnZgqygULPCJ+G/hOZh6+mDfIzH2ZOZGZE+Pj4xfzI6Sh+uEPfwjAj370o4qTSIPpZyfm64A3R8SbgCuAnwceBK6JiLHeLPxGYGF4MaXhaLfbHDx4EIDPfe5ztNttZ+EqxgVn4Jn5zsy8MTO3A/cAn8nM3wMeA97Su60JPDK0lNKQfOADHzj9McLl5WX27dtXcSKpf2v5HPg7gLdHxFG6a+IPrU8kaeMcOHDgrPHc3FxFSaTBDXSYVWZ+Fvhs7+ungVvXP5K0cbofqDr/WNrM3ImpWtu5c+eqY2kzs8BVa9PT06c/Bz4yMsL09HTFiaT+WeCqtUajcXr35a5du/wEioriAx1Ue9PT0xw/ftzZt4pjgav2fCKPSuUSiiQVygKXpEJZ4JJUKAtckgplgUtSoSxwSSqUBS5JhbLAJalQFrgkFcoCl6RCWeCqvXa7zZ49e2i321VHkQZigav2Wq0W8/Pz7N+/v+oo0kAscNVau91mZmaGzGRmZsZZuIpigavWWq3W6YcaLy0tOQtXUSxw1drc3BydTgeATqfD7OxsxYmk/lngqrXJyUnGxrrH4o+NjZ1+Oo9UAgtctdZsNk8/iX5kZITdu3dXnEjqnwWuWms0Gmzbtg2ArVu3+kxMFcUCV621220WFhYAWFhY8FMoKooFrlprtVpn/RLTT6GoJBa4am12dpbMBCAz+fSnP11xIql/Frhq7dw17y1btlSURBqcBa5a+/a3v33W+NR6uFQCC1y1dmr55HxjaTOzwFVrFrhKZoGr1kZGRlYdS5uZ/1pVa7fddttZ49tvv72iJNLgLHDV2qlt9FKJLHDV2sGDB1cdS5uZBa5aO3cG7oxcJblggUfEiyLisYh4KiKejIj7e9evjYjZiPh6788XDj+utL5e//rXrzqWNrN+ZuAd4M8y85XAa4E/iohXAg8ABzLzZcCB3liStEEuWOCZeTwzv9T7+n+BI8A24C6g1butBdw9pIzS0LgGrpINtAYeEduBVwOPA9dl5vHeSyeA687zPdMRcSgiDi0uLq4lq7TuTj0P83xjaTPru8Aj4gXAx4E/ycz/OfO17G5fW3ELW2buy8yJzJwYHx9fU1hJ0k/1VeARcRnd8v5QZn6id/lkRNzQe/0G4DvDiSgNz/XXX3/W+IYbbqgoiTS4fj6FEsBDwJHM/OszXnoUaPa+bgKPrH88abhOnjx51vjEiRMVJZEGN9bHPa8Dfh+Yj4gnetfeBfwl8LGIuBd4BnjrUBJKQ+QauEp2wQLPzH8Dzre7Yef6xpEk9cudmKq1c9e8t27dWlESaXAWuGrtlltuOWt88803V5REGpwFrlr7/Oc/v+pY2swscNVap9NZdSxtZha4am1paWnVsbSZWeCSVCgLXJIKZYFLUqEscEkqlAUuSYWywCWpUBa4JBXKApekQlngklQoC1ySCmWBS1KhLHBJKpQFLkmF6ueZmLoEvf/97+fo0aNVx9iU7r///qojVGrHjh3cd999VcdQH5yBS1KhnIHXlDOsrre97W0cOXLk9PgVr3gFDz74YIWJpP45A1etvec971l1LG1mFrhqrdFocMUVVwDd2Xej0ag4kdQ/C1y195KXvISrr77a2beKY4Gr9i677DJ27Njh7FvFscAlqVAWuCQVygKXpEJZ4JJUKAtckgpVq52Ynv+hlZz6N1H3M1D0szb7uTC1KvCjR4/yxFePsHTVtVVH0SYy8uME4PDTJytOos1k9Ln/rjrCBdWqwAGWrrqW51/+pqpjSNrkrvzap6qOcEGugUtSoSxwSSqUBS5JhVpTgUfEVET8R0QcjYgH1iuUJOnCLvqXmBExCvwtsAt4FvhiRDyamU+tV7j1trCwwOhzPyjilxOSqjX6XJuFhU7VMVa1lk+h3AoczcynASLiI8BdwKYtcACWOow+1646RfWWlyCz6hTajCJgZLTqFNVb2tzlDWsr8G3At84YPwv8+rk3RcQ0MA3w4he/eA1vt3ZveMMb3MjTs7CwwPPPP191DG1CV155Jdu2bas6xqawY8eOqiOsauifA8/MfcA+gImJiUqnfJt5R5UkDWotv8RcAF50xvjG3jVJ0gZYS4F/EXhZRNwUEZcD9wCPrk8sSdKFXPQSSmZ2IuKPgX8FRoF/yMwn1y2ZJGlVa1oDz8xPAX4mT5Iq4E5MSSqUBS5JhbLAJalQFrgkFSpyA7dTR8Qi8MyGvaHUvy3Ad6sOIZ3HL2bm+LkXN7TApc0qIg5l5kTVOaRBuIQiSYWywCWpUBa41LWv6gDSoFwDl6RCOQOXpEJZ4JJUKAtcl6yIuD4iPhIR34iIwxHxqYi4OSKej4gnIuKpiNgfEZf17r8jIj7Z+/oPIiIjYvKMn3d379pbqvo7SWeywHVJiogA/gn4bGa+NDNfA7wTuA74Rmb+KvBLdB9E8tbz/Jh5uufcn/K7wFeGFloakAWuS9WdwE8y8+9PXcjMr3DGc1wzcwn4At3nu67kIHBrRFwWES8AdgBPDC2xNCALXJeqVwGHV7shIq6g+yDumfPcksAc8JvAXfjEKW0yFrjq6KUR8QRwEjiemf++yr0fobuMcg/w4Q3IJvXNAtel6kngNed57dQa+EuB10TEm8/3QzLzC3TXyrdk5n+ue0ppDSxwXao+A/xcREyfuhARvwy86NQ4M78LPED3l5ureQB41zBCSmthgeuSlN0txr8DTPY+Rvgk8BfAiXNu/Wfgqoi4bZWf9S+Z+djQwkoXya30klQoZ+CSVCgLXJIKZYFLUqEscEkqlAUuSYWywCWpUBa4JBXq/wFRWV5VfjXbRAAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"col_x= \"CRIM\"\n",
"df_x = pd.DataFrame(df_xs[col_x])\n",
"sns.boxplot(data=df_x)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]),\n",
" [Text(0, 0, 'CRIM'),\n",
" Text(1, 0, 'ZN'),\n",
" Text(2, 0, 'INDUS'),\n",
" Text(3, 0, 'CHAS'),\n",
" Text(4, 0, 'NOX'),\n",
" Text(5, 0, 'RM'),\n",
" Text(6, 0, 'AGE'),\n",
" Text(7, 0, 'DIS'),\n",
" Text(8, 0, 'RAD'),\n",
" Text(9, 0, 'TAX'),\n",
" Text(10, 0, 'PTRATIO'),\n",
" Text(11, 0, 'B'),\n",
" Text(12, 0, 'LSTAT')])"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAETCAYAAAA8rh0/AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAvaklEQVR4nO3de5wU1Zn/8c/DVQQVGZGboAbQxFXjBY0aNQqKiEbcrHGjuKJhg0uQjb+IGqNZk6zxghqNm4TVSAwmE41xYzRCvIHZGBNNwAsQTeIMGxUGuYyKIigMPL8/zmnpbnpm+lI9Pd1+36/XvKbrdHWdU91VT51z6lSVuTsiIlJ7ulS6ACIiUh4K8CIiNUoBXkSkRinAi4jUKAV4EZEapQAvIlKjulW6AAC77bab77XXXpUuhohIVVm0aNFad+/f2vudIsDvtddeLFy4sNLFEBGpKmb2Slvvq4tGRKRGKcCLiNQoBXgRkRqlAC8iUqMU4EVEapQCvIhIjVKAFxGpUe2OgzezfYGfpSV9BPgP4K6Yvhfwd+BMd3/TzAz4DjAe2ACc5+7PJltsEekMZs2aRWNjY0ZaU1MTAIMHD85IHz58OFOnTu2wskkeNXh3/6u7H+TuBwGHEoL2/cBXgPnuPhKYH6cBTgZGxr8pwKwylFtEOqmNGzeycePGShdDKPxK1jFAo7u/YmYTgONi+hzgN8BlwATgLg+PinrazPqa2SB3X5lQmUWkk8hVI58xYwYAN954Y0cXR7IU2gf/OeDu+HpAWtB+HRgQXw8BXkv7zPKYJiIiHSjvAG9mPYDTgJ9nvxdr6wU93NXMppjZQjNbuGbNmkI+KiIieSikBn8y8Ky7r4rTq8xsEED8vzqmrwCGpn1uj5iWwd1vd/dR7j6qf/9Wb4YmIiJFKiTAn8W27hmAB4FJ8fUk4IG09HMtOAJYp/53EZGOl9dJVjPrDZwIXJCWfB1wr5lNBl4Bzozp8whDJBsII27OT6y0IiKSt7wCvLu/C9RlpTUTRtVkz+vAtERKJyIiRdOVrCIiNUoBXkSkRinAi4jUKAV4EZEa1Skeui0inVuum4q1JjVf6pYFbdENyMpLAV5E2tXY2MiLf2lgp92GtTtvCz0AeG3tpjbne2ftq4mUTVqnAC8iedlpt2F8YsJXE1veMw9ck9iyJDf1wYuI1CgFeBGRGqUALyJSoxTgRURqlAK8iEiNUoAXEalRCvAiIjVKAV5EpEYpwIuI1CgFeBGRGqUALyJSoxTgRURqVF4B3sz6mtl9ZvYXM3vJzI40s35m9piZvRz/7xrnNTO71cwazGyxmR1S3lUQEZFc8q3Bfwd42N0/CnwceAn4CjDf3UcC8+M0wMnAyPg3BZiVaIlFRCQv7QZ4M9sFOBaYDeDum9z9LWACMCfONgc4Pb6eANzlwdNAXzMblHC5RUSkHfnU4PcG1gB3mtlzZnaHmfUGBrj7yjjP68CA+HoI8Fra55fHNBER6UD5BPhuwCHALHc/GHiXbd0xALi7A15IxmY2xcwWmtnCNWvWFPJRERHJQz4Bfjmw3N2fidP3EQL+qlTXS/y/Or6/Ahia9vk9YloGd7/d3Ue5+6j+/fsXW34REWlFuwHe3V8HXjOzfWPSGOBF4EFgUkybBDwQXz8InBtH0xwBrEvryhERkQ6S7zNZpwP1ZtYDWAacTzg43Gtmk4FXgDPjvPOA8UADsCHOKyIiHSyvAO/uzwOjcrw1Jse8DkwrrVgiIlIqXckqIlKjFOBFRGqUAryISI1SgBcRqVEK8CIiNUoBXkSkRinAi4jUKAV4EZEapQAvIlKjFOBFRGqUAryISI1SgBcRqVEK8CIiNUoBXkSkRinAi4jUKAV4EZEapQAvIlKjFOBFRGqUAryISI3KK8Cb2d/NbImZPW9mC2NaPzN7zMxejv93jelmZreaWYOZLTazQ8q5AiIiklshNfjj3f0gd089fPsrwHx3HwnMj9MAJwMj498UYFZShRURkfyV0kUzAZgTX88BTk9Lv8uDp4G+ZjaohHxERKQI+QZ4Bx41s0VmNiWmDXD3lfH168CA+HoI8FraZ5fHNBER6UDd8pzvaHdfYWa7A4+Z2V/S33R3NzMvJON4oJgCMGzYsEI+KiIiecirBu/uK+L/1cD9wOHAqlTXS/y/Os6+Ahia9vE9Ylr2Mm9391HuPqp///7Fr4GIiOTUboA3s95mtlPqNTAWWAo8CEyKs00CHoivHwTOjaNpjgDWpXXliIhIB8mni2YAcL+Zpeb/qbs/bGZ/Au41s8nAK8CZcf55wHigAdgAnJ94qUVEpF3tBnh3XwZ8PEd6MzAmR7oD0xIpnYiIFE1XsoqI1CgFeBGRGqUALyJSoxTgRURqlAK8iEiNUoAXEalRCvAiIjVKAV5EpEYpwIuI1CgFeBGRGqUALyJSoxTgRURqlAK8iEiNUoAXEalRCvAiIjVKAV5EpEYpwIuI1CgFeBGRGqUALyJSo/IO8GbW1cyeM7OH4vTeZvaMmTWY2c/MrEdM7xmnG+L7e5Wp7CIi0oZCavBfAl5Km74euNndRwBvApNj+mTgzZh+c5xPREQ6WF4B3sz2AE4B7ojTBowG7ouzzAFOj68nxGni+2Pi/CIi0oG65TnfLcClwE5xug54y91b4vRyYEh8PQR4DcDdW8xsXZx/bfoCzWwKMAVg2LBhRRZfRCQZs2bNorGxMSOtqakJgMGDB2ekDx8+nKlTp3ZY2YrVboA3s1OB1e6+yMyOSypjd78duB1g1KhRntRyRUTa01ow37hxY0Zaajo7vampabvPQ+cL/PnU4D8JnGZm44EdgJ2B7wB9zaxbrMXvAayI868AhgLLzawbsAvQnHjJRUSK9OSTT/LG2jfo2bVnm/N18dCLvfW9rRnp7773Li+/+XJG2vtb3qepqam6Ary7Xw5cDhBr8DPcfaKZ/Rw4A7gHmAQ8ED/yYJz+Q3x/gburhi4inUrPrj3Zc6c9E1veK++8ktiykpJvH3wulwH3mNnVwHPA7Jg+G/ixmTUAbwCfK62IIiLJGjx4MJtaNnH5qMsTW+a1C6+lx+AeiS0vCQUFeHf/DfCb+HoZcHiOed4DPptA2UREpASl1OBFRKrWq+tf5dqF17Y5z6oNqwAYsOOAvJY3ghGJlC0pCvAi8qEzfPjwvObb1LgJgB7D2u96GcGIvJfbURTgReRDJ9+RLjNmzADgxhtvLGdxykY3GxMRqVEK8CIiNUoBXkSkRinAi4i0YsOGDSxdupRly5ZVuihFUYAXEWnF3//+d7Zu3cpVV11V6aIURQFeRCSHhoYGWlrCDXNXrVpVlbV4DZMUEWH7O0y++OKLGe9feOGF7LfffkDnu2tka1SDFxHJIVV7b226GqgGLyLC9hc/jR07drt5qu2CJ9XgRURqlGrwItKupqYm3nn7XZ554JrElvnO2ldo2tQ7seXJ9lSDFxGpUarBi0i7Bg8ezJYem/jEhK8mtsxnHriGwbt1rgdkpDMz0h9GZ2YVLE1xVIMXEckh+0mj1fjkUQV4EZEa1W6AN7MdzOyPZvaCmf3ZzL4R0/c2s2fMrMHMfmZmPWJ6zzjdEN/fq8zrICIiOeRTg38fGO3uHwcOAsaZ2RHA9cDN7j4CeBOYHOefDLwZ02+O84mIVJXu3bu3OV0N2g3wHqyPk93jnwOjgfti+hzg9Ph6Qpwmvj/GqvHshIh8qG3evLnN6WqQVx+8mXU1s+eB1cBjQCPwlrunrt1dDgyJr4cArwHE99cBdQmWWURE8pBXgHf3Le5+ELAHcDjw0VIzNrMpZrbQzBauWbOm1MWJiEiWgkbRuPtbwBPAkUBfM0uNo98DWBFfrwCGAsT3dwGacyzrdncf5e6j+vfvX1zpRUSkVfmMoulvZn3j617AicBLhEB/RpxtEvBAfP1gnCa+v8CrcQCpiEiVy+dK1kHAHDPrSjgg3OvuD5nZi8A9ZnY18BwwO84/G/ixmTUAbwCfK0O5RUSkHe0GeHdfDBycI30ZoT8+O/094LOJlE5ERIqme9GISF7eWftqXneT3LBuFQA77jKg3eWx24hEylYOxxxzDE8++eQH08cee2wFS1McBXgRadfw4cPznrdx3SYAhrZ3I7HdRhS03I521llnZQT4s88+u4KlKY4CvIi0q5Dnj86YMQOovqcfZZs3b94Hd5Q0M+bOncv06dMrXayC6GZjIiI5LFiw4IM7SLo78+fPr3CJCqcALyKSw6GHHpoxfdhhh1WoJMVTgBcRyWHZsmUZ042NjRUqSfEU4EVEclixYkXG9PLlyytUkuIpwIuI5NCnT582p6uBAryISA4fmtsFi4h82AwcOLDN6WqgAC8iksPrr7/e5nQ1UIAXEcnhQ/HIPhGRD6P169e3OV0NFOBFRHLo3bt3m9PVQAFeRCSHjRs3tjldDRTgRURy6NKlS5vT1aD6Siwi0gGOO+64jOnjjz++MgUpgQK8iEgOkydPbnO6GijAi4i0ItUtU43dM5BHgDezoWb2hJm9aGZ/NrMvxfR+ZvaYmb0c/+8a083MbjWzBjNbbGaHlHslRESSVl9fnxHg6+vrK1yiwuVzWGoBLnb3/YAjgGlmth/wFWC+u48E5sdpgJOBkfFvCjAr8VKLiJTZggULaGlpAaClpaU2H/jh7ivd/dn4+h3gJWAIMAGYE2ebA5weX08A7vLgaaCvmQ1KuuAiIuU0evRounULTzXt1q0bY8aMqXCJCldQx5KZ7QUcDDwDDHD3lfGt14HUI9SHAK+lfWx5TBMRqRoTJ07M6KKZOHFihUtUuLwDvJn1Af4HuMjd305/z8ODC72QjM1sipktNLOFa9asKeSjIiJlV1dXx9ixYzEzTjrpJPr161fpIhUsrwBvZt0Jwb3e3X8Rk1elul7i/9UxfQUwNO3je8S0DO5+u7uPcvdR/fv3L7b8IiJlM3HiRPbff/+qrL1DfqNoDJgNvOTu305760FgUnw9CXggLf3cOJrmCGBdWleOiIh0kG55zPNJ4F+AJWb2fEz7KnAdcK+ZTQZeAc6M780DxgMNwAbg/CQLLCKdx6xZs7Z7GHVqesaMGRnpw4cPZ+rUqR1WtiTU19ezdOlS6uvrmT59eqWLU7B2A7y7/w6wVt7e7rRy7I+fVmK5RKRK9erVq9JFSERzczOPPPII7s4jjzzCxIkTq64fPp8avIhITtVWIy9EfX39B+PgN2/eXJW1+Oq8/lZEpMzmz59P6JAAd+fxxx+vcIkKpwAvIpJDdndMXV1dhUpSPAV4EZEcVq7MHPzX1NRUoZIUTwFeRCQHPfBDRKRG6YEfIiI1avLkyRn3otEDP0REakRdXR2jR48GYMyYMVU3Bh40Dl5EpFWTJ09m1apVVVl7BwV4EZFW1dXVcdNNN1W6GEVTF42ISCuam5u5+OKLeeONNypdlKIowIuItGL27NksWbKE2bNnV7ooRVGAFxHJobm5mQULFgDhtgXVWItXgBcRyWH27Nls3boVgK1bt1ZlLV4BXkQkhyeeeCJjOlWbryYK8CIiOYSH2bU+XQ0U4EVEctCtCkREalT2xU3VeLGTAryISCvS70VTjdottZn90MxWm9nStLR+ZvaYmb0c/+8a083MbjWzBjNbbGaHlLPw5VbtFzmISPHq6+s/6Hc3M+rr6ytcosLlc1j6ETAuK+0rwHx3HwnMj9MAJwMj498UYFYyxayMmTNnsmTJEmbOnFnpoohIB1uwYAFbtmwBYMuWLcyfP7/CJSpcuwHe3X8LZFdhJwBz4us5wOlp6Xd58DTQ18wGJVTWDtXc3Mxzzz0HwLPPPqtavMiHzAEHHJAxfeCBB1aoJMUr9mZjA9w99Tyr14EB8fUQ4LW0+ZbHtMxnX5WoubmZa665hiuuuKJst/DMrrXPnDmT6667rix5SeXNmjWLxsbGjLTUI9oGDx683fzDhw9n6tSpHVI2qYzFixdnTL/wwgsVKknxSj5z4OGx417o58xsipktNLOFa9asKeiz9fX1LF26tKx9Yqnae8qzzz5btrykc9q4cSMbN26sdDGkQrJ/+2rcFoqtwa8ys0HuvjJ2wayO6SuAoWnz7RHTtuPutwO3A4waNSrvA0RzczOPPvoo7s4jjzzCxIkTq/JG/FI5uWrrhWpsbGTGjBkZaarVS2dTbIB/EJgEXBf/P5CWfqGZ3QN8AliX1pWTiPr6+oz7Q9TX1zN9+vQks5Aa19jYyOK/vITV9W1zPvewnS1Z0/4m7M1vJVAykWS1G+DN7G7gOGA3M1sOXEUI7Pea2WTgFeDMOPs8YDzQAGwAzk+6wAsWLKClpQWAlpYW5s+frwAvBbO6vnQ77bjEltfy4G8SW5ZIUtoN8O5+VitvjckxrwPTSi1UW0aPHs3cuXNxd8yMMWO2K4aIiFCFj+wbP348Dz30EADuzimnnFLhEkm1aWpqwt9el2it25vfomlzwWMNpBPr2rXrB+PgU9PVpuquv503b17G9Ny5cytUEhGpZUcddVTG9NFHH12hkhSv6mrw2VeTPf744+qDl4IMHjyY5u6WeB/84P5VeU2f5Cn0QFeXqqvB77777m1Oi4gk4fe//33G9FNPPVWhkhSv6gL86tWr25xOSvfu3ducFhHp7KouwGePmjnhhBPKkk9qKGZK+skWEal9AwcOzJgeNKj6uuCqLsCPHz8+Y7pco2iy+9tSF1eJyIdD9g0Gm5ubK1SS4lVdgNcoGhHpCKNGjcqYPuywwypUkuJVXYDPNYpGRCRpy5Yta3M6SQ0NDZx++umJ51F1wyT79evHihXb7l9WV1dXwdJItfLmt9q90MnXrQfAdumT1/LQMMmakh5nAJYvX162vL72ta+xYcMGrrzySn76058mttyqC/ArV2be+Cl1z26RfA0fPjyv+RrfDnecHJ5P4O4/KO/lSnXo06cP69evz5guh4aGhg/699euXcuyZcv4yEc+ksiyqy7AZ5/s1MlPKVS+t/RN3Q74xhtvLGdxpJPavHlzm9NJ+drXvpYxnWQtvur64EVEOkL2MMns6aRkj85Zu3ZtYsuuuhr87rvvnnFx04ABA9qYO3/5PAQiVaPTgx1Eal92d3D2dLE6MtZUXYB/7733Mqar6TFaeu6nSPXIvrixGi92rLoA//bbb7c5XazsQDp27Njt5ilHX2w1HaCkPEp9iHxrFYd8t61evXptV8Ho7JWLL37xizQ0NLDPPvvw3e9+tyx5lCvAZ3+vl112WcYzoA899FCuvfbaRPKqugDfUS6//PKML/nKK68seZm5dhidyCvOpEmTWLlyJUOGDOHOO++sdHFKMnPmTJYsWcINN9xQ1I4dHkH4N7rWbesj3rrhfTzrdhut2eDv8+aabRWlLc2vF1yGpEydOpXXX8/M//333291cMXf/vY3xo0bl/Fely5d6NmzZ0bawIEDmTVrVhlKXLpLL72Us87a9lylSy65JLFlK8C34vjjj8/Y2Y499tiCPp/vg51T82Q/wLk1nb1m1VFS/aHZY5WrTXNz8we1t0WLFvHGG28UVYvvWjeQHU/710TKtOHBOxJZTjHWrVvHu+++W9BncgX/7HtJrVu3ruSyFSPfOGBmuDu9e/fmmmuuaXPeQmLAhy7A5/uFA/To0YNNmzYxdOjQdgNw9pfe2NjIX19azIC+1ubnumwN97x5a+WSdsuz6q3i70ed3uX06KOPFr2czmDSpEkZ0+eff37V1uJnzpyZMV1sLb5WHHPMMe12N+U6APTu3fuD1611OVVCY2MjDS/+lWE7tz0CZ+fuO7J+83sM6r4rm5a3fjB69e3CWldlCfBmNg74DtAVuMPdryt2WUmfcW5sbOTlF5cwbJf2b//bu0sLvXfowo4bVvH+hlWtzvfquu3Hx+Z7Adaufdo+ABS73FqWPZqhmmrx2dvz4sWLM95ftGjRh3q0Vq71be87g8wAntT3lqrgpU8XqqmpiXyqZYP67JbX8pzCYkDiAd7MugLfA04ElgN/MrMH3f3FpPMq1rBdunPZJ5N7UMj1T+W+J/2mlvZr3S3xvE23PB73uCm/LtXtZJ8wHjt2bKesxc+aNStnuTZs2NDu03RS62hm7Ljjjtu9V4lAWezJz9RnmpqaclZusgNYU1MTW95+J7GulS3NK2navL79GTtIpQZApAf3XNP5er9lE6+0U/PevCXs3N27th2S32/ZRO8258hUjhr84UCDuy8DMLN7gAlAuwG+kO6TXBobG7frSqlULShXUzOX1Dz5NiE70+XwhQz77Oy10Vzr0tb5kXzW58knnyzqopVUF8S7776b8/NNTU3b5715E1ua01o2LS3geV7lbV2gW1oo2FxcIOsoI0aMoKGh4YPpffbZp4KlaVs+XU4AWzeGXoAuPTNDcqndTeUI8EOA19KmlwOfyOeDxe4QuZpsKdk7Q1NTE280b2LavMxm/eYtztY8u7i7GHTvuq1r5f0Wp59lNpvyaWq2J58gkqvWW2qNN/V+et6F5pP9Oy5ZsmS7z2fnMXXq1LwOArlqcOVokfTq1aukz++yyy7b7cjZI0LcPeM7NDPMwraVazRIarnp8g0irelMfdb5+P73v5+xDZRrmGQS8o0D5aoYVewkq5lNAaYADBs2DMhvh4DMs+ZdunTJeJ29Q2TvDLnyiBlBvve16dKFLmn59Oq5fT75KjWIVFLXrl1b/W3Sf5dc051NOVoX+Q7LGz9+PC0tLXTr1m275x3kozO3jMolVYvvzLX31nTk72VJPynczI4Evu7uJ8XpywHcvdWhAaNGjfKFCxfmncc555zD6tWrGThwIHfddVepRa55HVXj7ShPPPHEdtcoFDqMtTNJrU+1r0etyb4A6ZBDDuG664oeL1IWZrbI3Ue1+n4ZAnw34G/AGGAF8CfgbHf/c2ufKTTAS+FqaZgk1N76SOfT3NyccQHSPffcU9Q1CuXUXoBPvN3s7i3AhcAjwEvAvW0Fd5FiXH755UAyVxiL5FJXV8fBBx8MhNp7Zwvu+Ui8Bl8M1eBFpDMq9T5B5dZeDf5DdyWriEi+6urquOmmmypdjKJ17qENIiJSNAV4EZEapQAvIlKjFOBFRGpUpxhFY2ZrgFcK/NhuQHJPp61sPrW0LrWWTy2tS63lU0vrUmw+e7p7/9be7BQBvhhmtrCt4UHVlE8trUut5VNL61Jr+dTSupQrH3XRiIjUKAV4EZEaVc0B/vYayqeW1qXW8qmldam1fGppXcqST9X2wYuISNuquQYvVcJST7AQkQ5VMwE+Pgs26WX2M7OKf0fVGiDN7OMAXqZmoplV79NSOoFyb1dmNrAc++WHjZm1OgyyPRUPXkkws3HAl80ssSdpm9lw4CpgbKWCvJntY2Y7lDFA7p3kd5a17B2B/zCz/cq0/PHAf5dr+Vl5nWJmZ5c5j7Fmdmk588hWxu2qi5ntAfwaGFaOPAooS38zG5AqVwGfqzOzXctXsrzLcSrwSzOrK+bzVR/gzaw7cAHwJeAUM0tqg1oNbAROAEZ3dJA3s1OAOcCnyrz8/cysRznyAPoBB5dp2acB/wRMM7NDy5QHZnYicANheyhXHicD3wZWxQNjKr0sNWwzG2NmN5rZr83sP8wssd/IzMzdt7r7cuAFYI9UelJ5FFCWU4B5wM/M7FfA1+OBp73PjSccnG4zs6vLXMy2ynEScB3w7+7eXMx3WPUB3t03A78C3iEEkxPMbEixyzOz3c2sv7u/A1wNvAFMAMZ0VJA3s7Ex7xnu/kjWeyXvKLHFcw3wDXf/jbtvKnWZacseYWYfcfcNwB1A/5jeI/5Pakf/ATAXWAacb2aJX4gSv6dbgfPc/XEzGxYDfpJ57A9cC0x29znxewPKU8OO6/Q94M/A3cABwAVm9tmEshgcn+oGsAk4HsK6dGQlyczGEH67SwmVtNuAnsCNbQX5+P18FfgWYR8ZVomuwBgDfgS8RngyXlGqNsDHJlQvAHf/IfA0sDNwLPBpMxvc1udbWeaRwP8BD5vZmcDH3f0awuXDnyR015StJpK27AnAd9z9KTPb2cz2NbN/i4GzpJ0+5jEGuMLd55tZXzPb38zONLOjsspR6LIHAZcA88zsv4GvEFpVuwBdYVvQKiYPM9sz5gHhaWHdgH0IwerzZnZIMeVuJa86YCrwW3f/Y5y+DxiZVB7RZuAP7v6Mme1qZhea2S/M7GEzOzktWJbMzI4H/gv4vLvf6e53ER58/xqhYlRSd5eZ7QY8Qagx/whYD+xtZnsCuHueT7UvqQwWt60jgWvc/Ql3b3H3hwgVjleBf2nls/0INf6b3P0BoAdwIuGgcFt6HmVeh/HATcDlwEOErs6PF7PvV+UwyRiIHwV+DMx197mxOdYNWEfYaP83vrc8z2WOBv4BOBA4G/gO8FHgTWA5MBxoBn7p7k8ku0YflKEuNsVuIux0jxBqILvG/N8Hprn7MyXmcwfQnRCMbwLqgD6EdZ/i7veWuPwRwE7APwJXEpq77wLPEb7D2e6+pcBlHgIsBP4IXEE4oNcRfuvfAocBg4C73P2PpZQ/Lc8JhECxkXDQ/Z67z05734o94Mb16UF4fvHPCevwL8DvgReBHYGjgX929zWlrEfMrwdhm+5NaBmuTnuvL2FfesrdS3qqdGw9vw+cQ6hwfZ2wL74GNMTXL7t7Uyn55FGObwI7uPulZtYtPkqUWHE7191PbeVzpxBaz+cBNxJ+jzsIv9H/uftZuT6XcNn/EWh299+a2YGE7shBwG3uvrighbl71f0BBwGPA48BS4HzgZnAk8BQ4BPAAzG9ax7LG00IQC8Sgun3gF8QDhinApfFfLYSDiw7lGGdhhE2pCOAj8V1WUroihgb5/kaUE88MBe4fEt7vTMhoLwU8xwd0/855lfQ8oGTCN0M98SN8cC0934JTCO0gK6P5d+70HITDkB3EfrCb4+/yW3ALYQD00DgPwkHrJ4l/A6fAr4MfCJOfwb4H+C+rPkmAV8oMo8ewL8DC4C9YvmnxXx3S5tvbqocCW1jewOzgG8CB2R9v18kHByLWW7PtNdd0l7vEPejvQmVppnAz4D+Sa1TVjn2AS6Kr88Afpr2Xvf4vxfwMLBzG8sZF/f1r6Sl9SHEnLpylD3mcQyhhdgr/bskdKNdQYhLBxS0zHIVtkxfwIHAVfH1kYQmzG2Ems9FwAZgenz/eGBwHss8CXg27rA/iWm9gZ8Cd6fN9xHgKGCfMq3bnoQa9e3A/oTusyFZP/Tk+CO3e9DKWvbRhO6GPmlpXbLXJQaY2ek7aR7LPo1woPgsobZ2AyEgpg5KNxFqocV+L+nBozehX/VJwgHxekLr6sb4/r6l7IDAeEIr4fPAQWnp4wi13wvj9OmEE4j7l5BX37jN/go4OMf7Z8U8BpW4Xe2eNT08bmPfIPNAfDnw9SKWf1L8vSdlpae22bnA2em/YSnr00Y59o1x4IdxXzbgN8A98f3Ugew84Kn0faGV5Z0I/BXoG6fPJ9TmdypT+XcktHD+TOgKPInMg+VB8TeaA/xD3sstR2HLsPIW/1I186/G9GNiQLkqTh8F7FvAck+MwenIOL0EOCS+3oVQY/wFRdSYi1zPYYTRQD8g1qrT1v+cGHzyDippG/XvCDWS3xFqNodlzdcHmAj8CdivgOX3I/S5HpGWNpRQG/05MCQGqnuAbkV8H2OB+wkHjs+klfUuYm2TMEpjZALf/dHAy+nrEtMPTyvLt+N6LQY+VkQeI+M2ejyxBsm2IH9EnN4nfn9LCtmRW8nvCEIr8DpCE3+XmD6CEOS/Cewef6MXgY8WuPz+hBOYq+J3ci/hQD8obZ4vEc73ZGyTCe83JxNaivsTWlw/ILRGuxBaSXcTKoJXELrE8tqH4nKXElo3vy1k3yuw/IPj/ysIJ1ZHEw7uVwD/mrX9XAIMzHvZ5ShwOf+AUTFgXBmnjwK+Tzih1+ZROWs53YDpwCfjdFdgPjAua75HgR+WaV1GA1/OStuT0HyfRTigdY9B4PfFbmBxR78mbhzXE4LypYTg2CPuDEsKXX7cwZ8i1ArTu4CGEWraYwgtrfsovNUxDngmBrtvxJ12ZHxvp7jT3pNUwCDU/qbF16na583AH4D/iMHiVEIXU94HwbTln0JoKd5PaOq/SmiR9iIEwV8Ramk7x/wKPoC0sq+8CjTGdZlNPGgAgwmtwYcItcaCDiaE1k4jcHjcVvcltHy+Sqg0jY2/0xGELpFeSf1WWeU4CXiebZW0nQiVmDuILce4LV0S96NCD2KnEkYDlXSwbaf8jxIqLnsTRoUdSohHNxLO/8wmVPD6FLwflaPQCX8BxwPfJTSt9otphxO6UFJB/kjgTkK/rOW7IRFrlWk79DcJJ6BS738GuJhwU/1yrNv+ceO5KCt9z7ijfClOD6aAo3b8zMDUxkCosd0PHBunv0io0X8/Bqw+FNAvSgjgO8XXd7Gt1dMtbZ4bgFvi6z0KLHu/WL5Ppz5PaJoemTZPD0Lrqj5OlxQ8CBe1/Txt+hBCIB5NCIRnx/SCuxhigHka+FRWfq8QD6qEg/pvgf1KWRe2tdpS2/QXCNeJfDy+Xhu38yPj93w9BbR64zJPItT4U62bm4GH4uujCCODfhG/v28SuzmS/ovleAtYlJXehxDkf0AY4lpqPjuWsfyLgaPT0i4gVDaOIRxAU+cAb6KI7rrEC12GL+C5uJH8LP7vGXfuTxBqcZfHeQ8HBhSZT2qnuAz4RXx9DqF5VtDGX0CeqeC7H+HE4YysspxE6I4q+IQuoZvkVuBcth3EziPU1s6JO+fZhPMKPwX2KmDZAwj90RcTahlXxt+od9Z8/w/4WgnfzymEmmWqK2MuoYvpFsK5gl1jgCrowJe9Lmmv9yM04w8iK8ASxkRPKzKP1MHq1Di9Q9p7X487cZ843wXA0BK3q55Z0xOBx+LrQYRRZlfHfK+k8JbVWEKXzH2ktTIIlYWrCTXQsYSW51HA8CT2lxzlOCrun0cAPyF00aR/t30IF8L9hHgyPPt3reRf/I7WE0aUpe/3JxCC/krgpNR7xcQB904c4AlDFLeyrdZ5OKEps3faPIfGoHVJQnkeGAPIP1Fgf3QBeRwTg+M9hK6RboRAu4q07hrCibx7KaL2QGgOX0yonZ3FtiB/O+FgMq6E8nchHCRuIQypJAbGRYQRKPsRDh5LSv3+CH2gLxPGbv+aMOxyCmGo5B20MRKigO3rZkLXgsVlfpO0kSvxN/pNKYGKcLBaQjwBTOaJ4yfY1gIqKNjmyCd1zuIq4J/S0m8j9EUvA06LabsDIwpc/hhCH/ZEwkH2urT983LCkOKjUttJUvtMG+uafu7nfkKQT/9udyIMby26ElCmsn+KcAL3vFjmS4Fd096/CpiXSF6VXtlWvoCDCScUfgn8OC39YcJ43QvjxtaNEOTbHS2TZ77D4k7/VxLoA82x/JPjsi+KO8djMVDuTejHfpXQFLuOcIApaEhUjvyuJFy4cUacPh/4Y9r7hYyWGUlszcRg+Gngv9lWO7okBsjHCMH4wFLKnpbvCfE3Sa9tdyFtOGGRy92D0CK4jNCVcAvwb4STqN+K6/F1wgGm5P7X+Ns3pnZktg3be6DU3zkuJ9c5i4/G9w4j1HZPidPF1QbDclIBfF/CsNTrCBWjXQh94acm8bu3U4YzWnnvl/GvR1pap6m1x/LsFfed1DDcA+K2dgnQL6aNIPRYlFzBrPgK5/gCxsUN5bMx8P0o7nQzCSf0ZhC6H14m1L6KHvOcI+/uhNpi4t0ybBuxc1ha2gGEEynfjtMfIdRQp1PgyJC4wz2UFjj6xx3+F4TRH/8Y0+cTh5IWsOy6GGRXxwDyb2yryX+dMAQz1eW0MwkPhYvB8UWyhvwlsNxvxx2pW1yXOwk17XGEcwjHUWAtN4/1SA/y58bfqKT1ovVzFqmROT0IB92LE1qPVP/+SEKL5wZCy21KnE5sn0zL0wg18iVsa3l9Lvu7i9v7AtKCfGf5I5yYnsu2E8KpfXU/tgX53nF7vI0EKq4VX+msL+BTMXCnB8E+hH609WQemftSYn9lK2XoXoZl9ibULP4re/mE2s9vgQklLD/V4rmfcEAcSmj6XxDf/yLhoDgp7hQFN1kJJxu3Eg4+txMOunfGDfHnhMCf+AVgaflPIIxCKbnpz7b+zh6ErrKBMZj/ndAquYcwMqRXGdbj5BikplLCyKgcy23tnMWthC6V8TGI9CHBWm3c7q4iVFSmFbNtFbEd3E9oZd1EGOV0Apldt/UUeGK/3H+Ec2ovEAaNpA6Q6SPP/oFwEP5movlWesWzvoQvs23kSPe09N6E0Ro/KUcALvM6DSa0DI6IAXF66sCUFmhuBW4tcvnjCCc5Uy2eOcAW0mrp8fubEXfEXUtYl1QrpEc8iEyKG2UzoQtglzJ/l3kPg81jWRbX4z9jQPgLcHp8bx9ic7lM61GWoXfkPmdxAeH6iURqhK3k+zHCMOVyXuWZ2ldGEk7yfyxO/4Bw/upu4Fvl3P5KKPsOhApeqqu0N7BbPOh2S1u3AwktkMS+x4qvfNaP91/A1elpafOk+uTv7siylbheAwlX1k2JASV1xn8aMCxtvquJJywLXH5rLZ4fk3aZdtpGVnRwT1vOKYQTban+wl0JJ+z2qvT3XeT67Au8TgkjforMt1xD78pyziKPfMtS8SIM7zyYtKuuCRWiOYSL014kdK+NIpx8L+nK3zKtQ1fC+alPEoZA30I497KS0BpJvz1Fol1LFV/5rC9iNOGE16FxugvbmjP/SjhBUdRQyAqu0+cJtafz4vqkgvyFhBrkGXEjLfhqTNpu8cwhjMIp15WDf0uyplHh3+g8wrmEsgTdCqxPWc5ZVGA9xsX1mEcYznt6TO9BuDDsbeK5pZhe0iikhMueXUG9iNCd9Cqh0vcZQqXvYdJuEZH0/prYrUgT8gyh3/CfzQx3XwRgZp8j1HofdvdVlSxgPsxsH8KReKm7/9DM1hJ+UAjB/buEpvOPCBc7fdbdXy5g+am7GO5NGNcM0JJ6393fjQ8quIGwYyR6Bzx3/3W8O+HjZnaod8BtYMvsabb9PlUv7fd52MxGVePvY2anEfrZxxJaJGcSus4AnHDeaq273x9v32txvs6iK9BiZj3cfZO732Jmvyacp3oh3uHSzexhQusaKMMzACp9pMtx5BtCuFT7fwknUa4m9I+W5T4QSR+1CUF3K+HulN8i3CBsJ0KQvZF4ZR3hQo0fU8JwTCrc4iHBPvFK/1Ejtfda+H0I56y+CmxISzuEcOL4MMJw5m6EvvdPV7q8Ocq/G+GEfaobM2e3C+GK1edLiQHt/XW2GjzuvsLMbiAMdTqB0E91mrv/rbIly0tXd/8/M7uIcOn5IEIz8hHC8MSDgT3NrJe7zzKzhV7a05Qq2uJx9/XlWnZH87QnKdWKavx9Ys19mrufFJ+g9Vd335dwwvhjhPN0PQmtrjsIV312Ku6+1symA783syPd/c344JYt7u7x/vsXEFol57j7S+UqS1U+8KMzik+zWUi4KvENM5tMGDFzBmHExMfi9CGE7pQD3H1da8srIN8hhFbCmJj/xpjnGe6+tNTli3QUC88gvZ5wW+bfxbTU+asn3H2cme1MGEhwIeEBLEU/zq7cLDxr97vAqFSQd/cWMzuccEuMeZ7nA4mKLoMCfHJi7eMGwgUmb5rZlwhXj37B3f9k4YHKvQjjqxP7YeOjCw9lW4vniSpp8YgAHzyDtJ4wumSqh2ctp967gXAydUSlylesHEH+QsLdQ48vd3AHBfjE5fhBpxNqIBe5+5MVLZxIJ2Rmnyacr7qbcMJxPeFBHa+lzfN9QpfGnu7+bkUKWqQYE64nDKr4AnCWuz/fIXkrwCcvR5C/lHD/iROB911fuggAZtaVcHO6l9396RjsxxCe1HVPei3XzL5N6JZprExpixef9Zp6etcLHZavYk15xCB/M+HmTG+Y2a7u/malyyXSWZjZiYQuzOeBP3l8mH3cd8YCKwgXNnbafvZCmNmOHX0yv0tHZvZh4u6/JtypcL6ZdSE8mEBEADMbR+iW+QNhGPG5ZnYUfLDvPEq4EvzzZja4YgVNUCVGanW6YZK1xN0fMLP5XoUXmoiUi5n1I1ydOsHdf2VmQwnXiOyemsfDxVqpezi9V5mSVj8F+DKrxrHIIuUUuyw/Dcw0s/9199fMbDPhaWGYWRd33+ruD8YKUlWdVO1MFOBFpMO5+1wz2wosMrNHgB0J90/C3bembseh4F4anWQVkYoxsxOI/e3uvtrMdnB3dckkRCdZRaRi3P1xwi2onzCz3RXck6UuGhGpKM+6+2VIUtdCEtRFIyKdgpn10aCEZCnAi4jUKPXBi4jUKAV4EZEapQAvIlKjFOBFRGqUAryISI1SgBcRqVEK8CIiNer/Axo0F5FBGhCWAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"sns.boxplot(data=df_xs)\n",
"plt.xticks(rotation=45)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Multivariate \n",
"\n",
"2차원 이상의 다변량 데이터에 대해 사용할 수 있는 비지도 학습 방법의 이상치를 탐지하는 방법에 대해서 다룹니다.\n",
"\n",
"데이터는 15% 의 Random uniform noise 를 포함하고 있는 여러 클러스터를 가지는 Scikit-Learn 에서 제공해주는 예제를 기반으로 Toy Dataset 에 대해서 각 알고리즘을 비교해보도록 하겠습니다.\n",
"\n",
"* IsolationForest: \n",
" * 공간을 분할하여 격자안에 데이터를 고립(Isolation)하는 방법으로 데이터를 분류하기에 이상치는 다수의 분할 없이 큰 격자의 영역을 가지는 점에 착안하여 이상치 정도를 판단합니다.\n",
"* LocalOutlierFactor: \n",
" * 데이터와 주변 데이터들의 거리를 통해서 밀도 기반으로 해당 점의 이상치 정도를 판단합니다, 데이터의 모든 점들에 대한 거리 계산이 필요하기 때문에 계산량이 많은 담점이 있습니다.\n",
" \n",
"참조:\n",
"* [Comparing anomaly detection algorithms for outlier detection on toy datasets](https://scikit-learn.org/stable/auto_examples/plot_anomaly_comparison.html#sphx-glr-auto-examples-plot-anomaly-comparison-py)"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Automatically created module for IPython interactive environment\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfkAAAOFCAYAAABpyZt3AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsnXd8VMX2wL+zJT0BUiD0ltB7B0FQUMEGoj57w4qK+mzPn/rU93z28qxgRaVZng0FLNgQVEroLfRQEgJpJCHJJrt75/fHbJJN2IQkZLObzXw/n/0ke+/ce8+9e2fOzJlzzggpJRqNRqPRaAIPk68F0Gg0Go1G4x20ktdoNBqNJkDRSl6j0Wg0mgBFK3mNRqPRaAIUreQ1Go1GowlQtJLXaDQajSZA0UreiwghPhRCeCVGUQhxvRBCCiHGeeP8Go2mIkKIca46d72vZakJQogUIcRvlbb9JoRI8Y1EGl/QJJW8W2W939eyVIdLzieEEM19LYsnhBCdXM+xqs/lvpaxJrie8RRfy9FUaSz1sS4IIVoKIZ4XQmwVQhQIIfKFEOuFEI8JIaLq4fx+/+66/b5VfUZ48drRrmd0ureu4e9YfC2AplrGAY8DHwLHKu2bC3wClDSsSB5ZCszxsP2vhhakjjwOfAR87WtBNIGDEGIk8C0QBcwHXgPMwBnAE8ANQohzpJQ7T+EytX13zwbEKVzvVPgYWOJh+24vXjMa9YwcwO9evI7fopV8I0VK6QScvpbDxU4p5TxvXkAIESmlzPfmNTSa+kIIEQ8sRLWxp0kp17jtnimEOBelmL8RQgyUUhY1hFxSynofFAghQgG7lNJxkqLrvN1ONDSNoV1qkub6qhBCXCuEWC2EOOYyre0VQswXQsRVKne6EGKpECJXCFEkhFgnhLixhtfoIYSY6TLf5QshCoUQa4UQN1Uq9yGqBwqwz8209YRrv8c5eSFErBDiTSHEQSFEievvm0KImErlSo8/UwhxvxBijxCiWAixUwhxXa0eXA0RQtzkelZFrmf3oxBitIdy0uXPMF4IsUIIcRw1Iird30wI8ZwQYrdL5gwhxMdCiC6VzhPiMtXtcD3nY0KIzUKIF1z7O4lyn4nr3E2I3rh/zalT0/fbVTZICPGgEGKD6/fPFUIkCSHudCvTRgjxkqtMjhDCJoTYJoT4hxDCfAqiPgDEAQ9XUvAASCmXAK8A3YGytsP1vkohRCcP91M2x17Xd1dUMScvhEgUQswVQhx2PdcUIcQLQojwSuU+dF0nTggxWwhxBCgA2lV33ZoihLhTCPGTECLNJUeaEGKOEKJDFeXHCyG+E0JkuX67vUKId4Uy008AdrmKPun2jHa7HW8RQvyfEGK76/gsIcQXQojela6T4Dr2USHEFa52zAb8tz7u25vokbwLIcQ1KLPXcuAxoAhoD5wLtAQyXOUuAL4C0oGXgHzgcuA9IUQXKeUjJ7nUOOB0YBGwDwgHLgXeFULESSmfcZV7G2Xmuwj4O5Dp2r6pmntoBvwJJACzgXXAQGA6cKYQYpiHXufTQKjresWush8KIXZLKf84yb2UEiKEiK20zS6lzHWT7TngQWA18DAQCdwC/CqEmOxq9NwZAlwMvIv6XSrfYwfXPW4FWgO3A6uEEEOklPtdxd8EpqGmEl5Gve+JwJmu/RnANaipj+XAOzW8X40PqM37LYQIAn5A1bcfgXmADegLTAXecJ22n+v7V8AewApMBJ4FugC31lHci1FTaR9WU+ZdVGfgYjd5akq9vbtCiMHAL6gpwbeBVKA/cBdwmhBirJTSXumwpag28ElUG3a8BpcK89BOFFdqkx4AVrjOn436faahft++UsocN7lvRz23g8As4ACqXbgQaANsAe4HXgQ+R1lWQLXZpXyCev4/ADNRbckdwFlCiNFSysrt7SUovTDL9cnF35FSNrkPquJL4H63bV8CeYClmuPMwH5UZWjjtj0I+ANlPk902/6hesQVzhHu4bwm4DfUC2N12/6ES85OHo653rVvnNu2p1zbbq9U9g7X9ic9HL8eCHLb3hal7D+uwXPs5DqHp89Kt3LdAQNVed2v1cb1LFMAs9v20nNM8HDNV1EdsP6Vtnd0/X4fum3LBpbU4D6k+3H607AfT/WxinK1eb8fdG172sN5TG7/hwLCQ5m5rvrc2oOc159EzkhXuU01uPc8INPte3V1PgX4rdK2Kt/dKsr/BqRU2rYRSAYiK22/qPL94mrTgHl1+H09fT6pVNZT+3iOq+y9bts6ojpRm4Goqn5jVIdQAo96KDPJtW+++zsADHL99r+6bSs9TzHQzZf1pbYfba4vJxcIA84TQlTlmDIY1whSSplWulGqea7nUcp6cnUXkVIWlP7vMifHoJxDfkSN3Hucwj1chOrhV+7Vv+3afpGHY2ZKt3k6KWUqsBM14q0pC4GzKn1muO2fjHL2eb7StdKAD1AVdmClc26UUv7kvsH1u1yFcqBJdZluY12jgwJgJcqxqJRcoLcQok8t7kXjv9Tm/b4KyAH+XfkkUkrD7f8i6WrFXeb9aNf79AOqPg+pg5ylXvM1GeXlAc3qcI16QQjRFzVaXgAEV6pTK1D16mwPh75Yh8u9w4ntxH/cC5S2j0IIk1DTcrHAWpSlYLhb0b+hrC5PSCnzKl/I/TeuhtL35anSd8B17DqUg+BYIUR0pWO+lafmKNngaHN9OU+jzOhfA1lCiGXAd8Cnstyc1Nn1d6uH40u3dfGwrwwhRASqt/43lNmnMi1qJ3YFOgNJspIDjJTSIYTYieqhVmavh21ZKMVbUw5VVsge5IKTP7ckt+2eKlIcEINqdDKquJZ75b4HNSLbLITYC/yKmtv/toaNgMa/qM37nQhskFLaqjuhEMICPARcixqtVe7g16U+liqdmijvKHxr8u3p+vsv18cTrTxsq4ui23WSdgIhxFnAoyiFHlxpt/tvUToIWV8HOUrpjPK63+Fh31bgfJS1Mttte6NS8KCVfBlSyl1CiF7AeNdnLGrO7F9CiNOllHvq6VILUC/PO6gRaRbKNHQuau69oa0rVXno+yrMppRCD9tKZfoJeO5kJ5BSLnQ5MJ2L+j0noJyclgshJkgveBprGh0vo6xOn6KmA44CdlSH4TnqUB+llPlCiANAdyFEmJTS07uMECIBZdr/zf3wak7tjfa6tE69BHxfRZmcyhuquqdTEkSFHH6HUqT/QPkslV7nf/iHo3i937e30UreDSllMcpMswRAqDCXxcC9qHm/0lFvbw+H93L99TQyxnW+5igFP1dKeVulfRM8iVQb+V3X7i6EsLiPdlyjlW7VyeZl3J9b5c7SSZ+bGxmoOfyok40ISpFSZqOcrua5zP3PouZrJ6MaDk3joTbv906ghxAi2FWvq+Ia4HcpZYXETS4FfCp8ibIkXQu8VUWZm9zKllI6aoxGzamXyhOCcgqr75jyUu9zZ03rlBe5EuX3NFFKeaB0oxAikhOtIqUj6gFU33ZU14buRXX8uwPbKu3r5Tp238nF9m/8oWfkF3jw+gTlvQuqwpV+P4BKYhHvdqwV5RUqKffg9ETpqLnCKFkI0ZryCu9Oqcdq5XmhqvgaZdKufK6bXdu/quF56ptvUM/mAdezAsru+waUM+NJzW4uE/t8YJgQ4hJPZYQQLV1/zaJSpkDXvFvpddyf6XFq/ow1vqM27/d8lHn30conqeRz4+TE+hiOsqqdCi+grHTPCCFOmCYTQpyDGjzsBN5321WqvCp3+quy8p3qu7se5YV+m6gUguqS0+JhXtpbVGVVfJQTLYv/Q1lcnnB1Airg9htX14aWJhD6v0rH9gfOA5ZJN2/+xooeyZfzoxDiGCoc5SDQnHIP9LmgEtAIFWP7FbBGCPEOKhzjMmAEypN3l4dz4zo+XwjxI3C1EKIIWIOa+74V1WOsHOu70vX3OSHEfFQI0BYp5ZYqLvE8KhzvTVfDsh7l0HYjat7p+Ro+i3pFSrlDqNj0B4HfhRCfUh5CFwFcJVVyn5rwCHAa8JkQ4jPUMypBPcdzUU4617vOf1gI8Q3qORxFzcFNR5kfv3U750pgghDiH6hOnJRSflL3O9bUkfGuEWtlMqWUb1G79/tV4ALgUSHEUJRjqw1lTepOuRL9HLjV9U7+hJp/noZS0HVGSpkmVLrZhcBfrvq7EjVSHYcKxToAXFjJ9P2T617+7XLK3QeMRrUvmZzIKb27UkrpCh/+BdgkhCgNSw1D+ShMRSnBD2t6zlPgS1TY3g+uttWB8qzvSaUpAynlfiHEfagsgpuFEHNQ998OmAJcjWorjwiVF+Aq19+jQL6UcrGU8jshxJeo9jgGZcEtDaErBO729g03CL527/fFB88hdDdTHvtZAhxG/ehneDh+rKtsHqrhWA/c6KHch5wYQhcLvAekuY7d7Lr29VQKiXOVfxBlVrK79j/h2l5V+ThUvOch1zGHUPHisZXKeTzete83KoXZVPEcO7nO8UYNn/vNrmdlcz27pcAYD+WqDWlDNUD/dD27IlRHazvKh2K4q0wQ8AwqLj8LFfqSgoqvTqx0vkSUEshzXVvW5H70p34+VB9iJYFkt7I1er9dZUNQncKtrnfuGKpjfbtbmTDUqHu/q8wulCPeeE4MHxtXeVsN7i0e5Ym+HaU4jgMbUImumlVxTDfU/HihS+bPUKGtKZwYElflu1tFeY91G9VJfst1TImrzqx11aH2buU+rG39oIYhkq6yF6MspoWo6bkFKMV9CPjJQ/mJqI5Rrqst2IOKtmjhVmYEKr9CgUuO3W77rKhOTDKqjchGdTZ6V7pOlaF4/v4RrhvQaDQajUYTYOg5eY1Go9FoAhSt5DUajUajCVC0ktdoNBqNJkDRSl6j0Wg0mgBFK3mNRqPRaAKUWsXJx8bGyk6dOnlJFI1GU5+sXbs2U0oZV9Pyun5rNI2HmtbvWin5Tp06kZSUdPKCGo3G5wgh9temvK7fGk3joab1W5vrNRqNRqMJULSS12g0Go0mQNFKXqPRaDSaAEUreY1Go9FoAhSt5DUajUajCVC0ktdoNBqNJkDRSl6j0Wg0mgBFK3mNRqPRaAIUreQ1Go1GowlQtJLXaDQajSZAqVVaW1+xZEMq365LpWfbZtw2PpEgi+6baDSBgGFIPvh9L0l7sxjbsyWXjeiIEMLXYmk0AYPfK/kN+3N4ftE2bHaDbam5CGDGOd19LZZGo6kHvlhzgLkr9mKzG2xPyyM2MoQJfeJ9LZZGEzD4bEjscBokp+WRmV9cbbk9R/KRUv1f7DDYnpbbANJpNJpTobDYwfbUXPKL7NWW256Wh81uAGCzO9mVnt8Q4mk0TQafjORtdic3vruStJwiDEPyzGUDGNXN84p5IxJieXPpToItJoSACwe1a2BpNRpNbTiaa+Pat/7E7jQQCN69eTid4yI8lp3Uvw0/b00HCULAGb1aNrC0Gk1g4xMlv2p3JodziigqcQIw86ddVSr5ttFhzJ0+ilV7sujSMoIBHVs0pKgajaaWfLPuEHk2O4ahFPeCP1N4ZHIfj2WHdonh7WnD2Hool4GdounS0nNnQKPR1A2fKPlmYUEYLhO8ENAi3OqxnJSSo3k2YiKCmTq0fQNK6Hs2HsjhQGYBw7vG0rJZiK/F0WhqTPOwIKwmE8WGgcVkIjo8yGM5h9MgM7+Yri0j6dGmWQNL6TuklPyxM4O8Ijtje7QiPMTvXaM0jRifvF0DOrbg8hEd+HzNQVo3D+VhD718h9NgxkdJbE3NxWwSvHLNYPp3aBqj+MXrU3lh8TYALGYTC+44jZZRWtFrGgeTB7dj3f5sVu3Ook+7Zlw3pssJZXIKSpj2zkqyC4oJD7bw/s0jaN081AfSNjz//S6Zb9elIpHMXraXBXecpiOGNF7DZ13I2yZ047YJ3arc/9fuTJIP51HiUE45r3yXzAe3jmwo8XzKl0kHy5yRQhCs3pPF+QPb+lgqjaZmWC0mnv7bgGrLfLXmIBl5NhyGxO4oYd6KfTxwfq8GktC3LNmQRpFdTVVmHy9m79H8JmXJ0DQsftt9DLKYoNSkDwRbzT6VpyHpFh/p1rOXdIwN96k8Gk19E2w1YTKpeHiTSTSp+t0hNgyzq3obEm2l03gVv1Xyw7rEML5PPCYBcVHBPHRB0+jlA9x9Tg/OG9CGPu2b8eD5vejbvrmvRaoRxXYn+zMLsLlGKRpNVUwd2p6ebaIQArrERXDdmM6+FqnBeP6KQZzeoxUDO7bg5asHER0R7GuRakSBzcGBzAIcTsPXomhqgZClQeg1YMiQITIpKcmL4pyIlFJnwGoEHM2zccPbf1FY4iTEamb2LU1njtVfEUKslVIOqWl5Xb81VbHl0DHu+igJQ0KbFqG8f/NwQoO0w6AvqWn99ouR/NFcG8u2HyH9WNEJ+3QD0Dj4YvUBjhWWUFTiJLewhE/+SvG1SBo/YV/GcX5PPkpuYckJ+3T9bhzMWrqLwhInNruTtJwiftt+1NciaWqIz7tie47kc9N7qzAJMAx468ZhdG8d5WuxNLUkPNiCSQicSMwmE+HBPn+1NH7A78lH+efnGzELNe8+//ZRjcY8rSknIsSi2mipfKTCgpqOD0Vjx+cj+cUb0igqcVJQ7KTI7mTh2kO+FklTBy4d3oF+HVpgNQt6t2vGVac1nTnW6ihxGOxKzyPvJOldA5V5K/ZRbDcoLHFSVOLkj50ZvhZJUwfuPbcHHWPDsZoFZ/RqxZjuOjMhKD+FXel52Er81w/J58OtdtFhhFhN2OwGwVYT7aLDfC2Spg6EBll48/qhvhbDr8grsnP9W3+RU1iCAN68fig92zatUKn2MWFsT8vF7lS+P9pPo3HSqlkoH9852tdi+BX7Mo5z83urMAxJWJCFj24bSUyk/1mpfD6Snzy4HRcOake76DDOG9CWvw3v4GuRNJp6Yenmw2QdL6aoxElhiZP3ftvja5EanL9P6sHo7i1pHx3GzWckMKRLjK9F0mjqhfkr9lFgc1BY4iSnsIRF61N9LZJHfD6SN5sE957bk3t9LYhGU89EhlrLHMssJkHzMM/pmwOZiBArz1xWfWIcjaYxEhVmxWIW2J0Si0kQGeqf9dvnI3mNJlAZ3zueM3q1JNRqplvrKO48u7uvRdJoNPXEtLFd6dOuOaFWMyMTY7nAT7OS+nwk74mDWQXcPWct6bk2zukbzz8v6luWHUujaSyYTYLHp/bj8am+lsS/WJeSzT8+Xo/N7uSWMxO4ZvSJue01Gn8nIsTKrGnDfC3GSfHLkfwLi7dzOLcIQ0p+Sz7KX7szfS2SRqOpJ/75v03k2xzYnZJ3f93jMT+GRqOpH/xSydvsTtwT8RXrNKkaTcBQ4iivzwLKFqHSaDT1j18q+bvO7k5YkJlgi4nOcRGM1jGZGk3AcO+5PbGaTQSZTUzoE0/7GB02q9F4C7+ck+/TvjmLHxhHToGd+GYhej5eowkgJvVvw2nd4rDZnXoFNo3Gy/ilkgeVXEUvgKDRBCZRoVai/DTkSKMJJPzSXK/RaDQajebUadChcnJaLj9uTqdrqwjO7d9Gr0Cl0QQQf+7MYM3ebIZ2jWZUYpyvxdFoNDSgkt+fWcBts9dgszsJsZo4kmtj2tiuDXV5jcZvyCko4dt1hwixmpk8uB3B1sa/oteKHUd55H8bKbYbfJV0gKf/NoBR3bSi1zQ99mcW8NOWw7RpEcbEfq19PphtMCW/+eAxSm/VZjdYnnzUq0o+r8jOnOV7KbI7uea0zsTrhTE0foDdYXDD23+RebwYkxD8sTODV68d4muxTpm/dmVSbFehcDa7wcrdmV5V8oeyC1nwRwoRIRauG9OF8BDtv6PxPUdzbdzw9l/Y7E6CLCZSMo4zfUI3n8rUYHPyvds2Q6KC30OsJkYkxHr1ejM+WsMnK/fz1ZqDTHt3JXYdi6vxAw7nFpFbaMfhlJQ4DNbuy/a1SPXC0K4xhFhVcxJiNXl1IZqiEgc3vrOSr5IO8vFfKdy3YJ3XrqXR1IYtqccQAgypOru/bT/qa5EabiTfuWUEr147hO82pJHQKpKpQ9t77VpSSnam55cl1CmwOcg8XtzklrnMLSwh2GomJADMwYFCy6gQgiwmbHYnZrMgsVWkr0WqF8b1bMVjU/uyalcWIxJjOb2H93JbpB+zYXcaSMDulGxLzfXatfwVKSU5BSVEhVqxmLX/tL+Q2CoSp6EUT7DFxMCOLXwsUQM73vXv0IL+Hbx/00II+rVvzvbUXJwSWoQHEeeH6/x6Cykl//5qM0u3pGMWgmcuH6AdofyEEKuZ924ezpzl+wgPtnDD2MDJ235mr3jO7BXv9eu0bhFKWJCFYoeB2SQY1Mn3DWlDYrM7ueODNexMzyMsyMJb04bRuWWEr8XSAO1jwnn12iF8ueYgHWPCuWZ0Z1+LFLghdK9cM5hbzkxk2uld+ODWkU2qt7szPZ9ftx3F4ZQUOwye/Wabr0XSuNE+JpxJA9qQXVDMF2sO4nDqqaTaEGI188GtI7j+9C5MH5/Ic5cP9LVIDcrPW9PZczQfu1OSV2TnjaU7fC2Sxo3+HVowMiGWvRnH+W5jGtI9R7sPCFhvldAgC1f7QS/KF5hNosz/ofS7xn9IyTjOvfPWYrMbBFtMZB8v4f7zevparEZFXFQIN5+R4GsxfIKqz6pOCwEWU9MZwDQGfk8+yrPfbsVmN1ix4ygWs+DcAb5bhla/HQFIQqtIpg5pj0lAeLCFx6f29bVIGjd2pedjcoXVFDsM1qcEhvOdpmGY0DueAR1bIFCdnbvO6e5rkTRubD6Qg80t0mR9So5P5QnYkXxT5+6JPbjjrG6YTcLncZqaivRt3xwAk4Agi4kze7XysUSaxoTFbOKVawbjcBpNahqysTAiMY7PVh+gxG4QbDUxtqdvF1jTSj6A0Q2AfxLfPJTZt4zgl61HaBcTxll9vO+spgk8dP32TwZ3jubVa4awdl8W/Tq0YKgXw0lrglbyGo0P6BQXwbRx2iNaowlEBnRswQA/CJ8DPSev0Wg0Gk3AokfyGr/GaUheWryN33dk0K9Dcx6b0peQIJ3cR6MJBI7b7Dz+xWZ2HM5jYr/W3HFWN+1DVM/okbzGr1myIZUlG9PIzC9mxY4MPlq+19ciaTSaeuKNH3eyek8mmfnFfL76IMuSfZ8GNtDQSl7j12TkFZetO1DiMEg/VuRjiTQaTX2RnmvD7lQ5PQwpycwr9rFEgYdW8pp640huEXfPSeKaWX/yx86MejnnxP5tCAu2EBFsIdRq5rKRHevlvBqNpnYkp+Vy47srufm9lexKz6uXc147pjMhVjPhwWbCgy2c0VuHk9Y3ojYp94YMGSKTkpK8KI6mMXP923+x83AehlSLM/zv7jG0jAo55fPmFpawMz2fznERxDahNQhOFSHEWilljdex1fVbUxUOp8HE53/luM0BQFSolR/+cUa9zJ8fyS3iQFYhPdtEERFiPeXzNRVqWr+1452m3kjLKcK1ABNmkyAjz1YvSr5ZWJDPY001mqZMUYkTW4mz7Ptxm51ih1EvK1y2ahZKq2ZNa4XQhkSb6zX1xiXD2hNiNRMWZKZVsxAS46N8LZJGo6kHIkOtDOsaQ2iQmdAgM2N7ttJLWDcS9EheU2/ccmYiw7rGcqywhBFdYwmy6D6kRhMovHDlIFbuzkQIGNE11tfiaGqIVvKaesVfsjxpNJr6xWwSnNYtztdiaGqJHmqdAvlFdopKHL4WQ6PR1DNSSo4VlJSFb2o0jRU9kq8jb/64k4//SkEIwSOTezOxfxtfi6TRaOoBpyG5f8E6kvZmYTWbeO3aIfRxrRyo0TQ29Ei+DhzNs/Hpyv04DIndafDcom2+Fkmj0dQTq/dksmF/DnanpLDEyYuLt/taJI2mzmglXwfMlWJDTTrXskYTMJhNFZtFs1nXb03jRSv5OhATGcyNZ3TFbBIEW0w8flEfX4vUpDAMyS/b0vk66SC5hSW+FkcTYAzpHM3pPVoiBDQLs/LQBb18LVKTwmZ3smh9Kks2pGqfiHpAZ7w7BRxOA5MQmEy6p9+QPP/tVr7beBgDSfOwID6dMVrH7HpAZ7w7NewOA4tZ6FXRGhApJTe/t4rdR44D0KddM964fqiPpfJPdMa7BsBi9n9DyLp163j22WfJz88HwGQyMXXqVKZNm9ZoG6+lW9IpsqvsW/lFdvYcyad3O+85Rm08kENuoZ1hXWL0MrdNCKvO89Dg5BXZSU7Lw+FKnbkuJZtiu5NgL3XinYZk9Z5MhBAM6xITkAM2reQDhGXLlrFw4UIMo9y8lZWVxaeffordbq9QdsmSJcyZM4eBAwfW6NyRkZFMnz4dIQSzZ89mypQp9O7du17lrw1dW0ay5dAxHIZESmjd3HspMd/7dTfz/kjBJCC+eQgf3TpKN/4ajZeICLESEWIht8iOAGIigr2aVOsfH69nbUo2ACMTYnn6sgFeu5av0Ob6AOCHH35g4sSJVe6fNm0aU6dOxWQykZyczBNPPEFeXt1XkQoODmbLli0kJCTU+RynwrGCEl77YQfZBcVMG9uVfh28l4DnnGd/IbdIdZLCgsy8ft0Qr1oN6hNtrtc0RvZnFvDm0h2YhGDG2d1pGx3mlesct9k557lfcbqsBiYBvzwyodFM/WlzfRNBSsmLL74IQM+ePbnlllsq7B80aBCnn3562fdJEydy8cUX88033+BwnDyRj2EYLFy4kN9//71sW3FxMQ888AAzZsxg6NChREZG1tPd1Izm4UE8NrVvg1wrvnko+TY7hlSmvbjIU19wR6PxGlJCI52GK6VjbDjPXzHI69cJsZoJtZo5XqzawYgQC0GNYAq2tuiRfCPnxhtvZPbs2YAa0Z999tmeCxblwNyz4fA6aH8aXLkYzFawnlxpGYbBBx98gGEY5Ofnc99995Xta9u2LTNnzmTAgAG0adMGi6Vh+o2L1qfyzbpD9GwTxR1ndfeaSe9IbhFPLdxK1vFibhufyJjuLb1yHW+gR/JNiMwdqn7npUL/a+DC98BwgKXxLc1sGJLZy/awak8WY3u25KpRnbzmP7QtNZcXF29DIHjwgl50b914FtXSI/kmwP79+8sU/Jw5c6pW8AArnoX0jSANOLSppTSsAAAgAElEQVQK/tsBSvKg41i4+jvPjcGWT2HRdEwmCzdOnQsJ5+B0OpFS8v3337N7925SUlKYPHkyAJ06dWL+/PmMGjXKG7dbxrqUbF5cvB2b3cmOtDxMQnD3xB5euVarZqG8dm2N9aRG4xsWTYfcg4BU9XbrZ+AohsG3wHlveh7d//oE/PkiRLSCK76Flv4RKvi/VfuZ98c+bHaDXel5tIwK4ey+rb1yrV5tmzH7lpFeObe/EHi2iQDH6XTynyefJDoyhE6dOgEwsF8frpk4FJxu5ve8NCjOL/9uL1QKHsCwQ/Ex9T11FWyaDzu+ha+uh3Wzlcmv+Dh8dR3YcqAwAz69GKTEbDZz3333sXTpUnbt2sUTTzxB586dCQ8PJyUlhdNPP50nn3wSp7N87en6Zt/R45RaoIodBjsO192/QKPxO4rzYcGF8EI8LL4D8tMha7eqlwCGoRS63VZ+jL0AcO132Fz13Qkb50BaEqx5S9Xv3T+oMmnr4M8X1HE5e+GraxryDqtlZ3o+Nrtqq2x2gz2ucDpN3dAj+UaAYRi88sorzJ8/n7S0NNLT08v2dWoOM4dth3eGQIsucOOf8M2NkLxQ9d5jukHOPmg3wu2MEhDqrzRUI7DxI9UwbPufahx6TqWs0QBwFitT4NfXqUbhtAexDJ3O448/zuOPP05JSQmPPvooL7zwAo899hg///wz8+bNo127dvX+PEYmxvHm0p2EWFUfdfLg+r+GRuMzfn0c9vyo6ty692Htu2CyQOIkmDIHPhgNmclgDoLwVlBwFDqO83wuacD6D8rr99bP4LpfVEdAuI3xbMeUpe/r61W5Sa9DQjWWQS9y7oA2/LQ1HYGyPpzRq5VP5AgU9Jx8I+DLL7/k4osvLvveKjqSD84t4oyODoLMyisUAGs4DJsBK18GZ+VMcCbAPXuUS8mX7ZPl33tdCn/7DJbMUI0MEsY8DCm/w76f1XdhgZv+grYVTdlLly7l2muvJT09nejoaGbPnl1mzq9PDh8rYtXuTLq2iqSvXjzEI3pOvpHy6SWw/YsTt1vDYNDNkDTLQ/12r8+Vv7vVfXMQTHhWtRNzJkDaGmUhuHg+LLodClwDCJMVHsyEEN/MUe9Kz2ProVz6d2xB57gIn8jg79S0fmtzfSNg165dAIwdO5YNGzawd+t6JvVtQUh4FCaTGXCbb1v9uocGACoqeKjYIBjl361h0MOllM99HW7fAnfugLH/hKOby8tJByS9Bft+U3P8rs7iWWedxcaNG5k0aRLZ2dlMmTKFn3/++ZTu3xOtm4cyZUh7reA1gcdpD6gOe3BUxdG24YQ1nhQ8VKzPlb8bIFxhYcICncaB2aJG9LckwT0p0PMiKDjidogddiyE3T9CRsMv0JMYH8WUIe21gq8HtLnez5FSsmzZMgCGDx9O//791Y67dsHh9aoxWHi9MqG3GaJM72WYXJ8arnnfqj+Mfgi6X6DOHZ0A0V0gJwWOHYCWfWGfW0OQvBC2fqpMgh3GwMAboOfFtGzZkkWLFnHmmWeybNky7r//fu655x5AJdY577zzCA5ufF6/Gk2D0G64qt+ZO5SH/FfXQnGeqt/7l5WXM4eA0+bhBJVH9agpuA6nw/inoFkHOLwB4npCTHfIVoMIwmKV/00p392jlL3hgD6XQ++/QcI5jT5Er6mhzfV+RmZmJrt37wagsLCQl156iSVLlgDwzTffcMEFF1R9cOoa+GAsOIrKt4VEgy27YrnIthDVwWWqq9QBiGqn5utKRwtdz4adi8Bph/A4OJ7uVrhSY2INh65nweVfAbBo0SKP8g4cOJAnn3yS1q1b069fvwYLu2tqaHN9gLH+A+WIV1q/hQmEFYziiuWad1Yj95w9VKifwgTxA1TnQQgIaQHN2qsOvbMEgptVbCuEFWRptkyhrHyjH4Kxj3rzLjU1pKb1Wyv5emT5jqPsSMvjtG5x9GzbrFbHSin58MMPmTFjBgUFBRX2tWjRgvfff5+LLrro5Cda+hD88Vw1BTz08t0xWVWvX55s9Sez6zyVywn4px3Myjy4aNEivvjiCwzDwDAMfvnlF9LS0spKDx8+nAULFtClS5eTXE9TW7SSrz+chmTJhlQy8oqZ2L8NbVp4L5VylRgGzJsEe3+sptBJ6vdJ95cWs6hyslKUTLOO8PeUkx+v8To6Tr6B+WbdIV5esp1iu8G8P/bxzo3D6VbDxAq5ubncdtttfPLJJwAkJiYSHR0NqNjzF154gfbt25/8RE67Mq1XSQ0quOHkRMVdCZNVmfGE2cPpJLwQp2Lv2w3n/PPP5/zzzy/bm5eXx8MPP0xSUhLJycmsWrWKAQMGMGfOHKZMmVL9dTUaH/HS4m0s2ZiG3WHw8V8pfH73GJqFBTWsEI4iyDtYTYEaKvCTIawuC19ls7yA3P3wagJc/6uyAmj8Hu14V0/8uvUINruBRPX6k/ZlV1u+sLCQW265hZYtWxIdHc0nn3xCeHg4H374ITt27GDlypWsXLmSTz75RCn47L1waHXFWHh38tPhlc6w7dNqrloaOlcdNVi/2XD17kt7+SYrtEgod+6x5ahQHA9ERUXxxhtvsHLlSvbt28eUKVPIz8/npptuOvl1NRofsXxHBja7gVOCIWHH4fyTH1RTpIQjmyF9U3ksfGXS1sILrSCzOic4WdFRr04Il4nezUpnsqoRvMlVv4+lwNJ/nOJ1NA2FVvL1xODO0WVx2yaToFfbZuw8nMflr6/gghd/ZcEf+zhuK18NbtasWbz77rtkZGRgGAZDhw5l/fr1XHfddRVTOObsgxdaw2tdYfZo+HDsiYo+LxVm9oH81BpIWg89/codAcMBncaCxS1FrqPSPKEHWrRowWeffQaoFfOeeuoprybR0WjqSr8OzctSJxuGpHNcOMt3HGXyy8u45NXf+XHzYYrtdXh3D/wJT0fArH7w7lCVua4yqUnw3khXwpuTcNJptpPVfw/7zUGQMEn9Lb2Gw5PDn8Yf0UrehcNp8NeuDJL2ZlEbP4VSrhzViekTunF233ieurQ/Azq24P4F60nJLCAjv4TXftzJhS8tIzktj9TU1LJFZe644w4yMzNZtWoViYmJJ57421vLY1cNu3KSSV1dvn/ZU/ByOyjKqstt1w9CQNdzVLIOczBYQuH8t2p0qNVq5amnngLg0UcfLUvTq9HUJ4XFDn5PPsr21Nw6Hf/Pi/py5ahOTOrXmpk3DCU0yMyjn23kSK6NQ9lFPPb5Ji55dTlZx0/eua3Ap1NV8hlQzm/r3y/PVCklfHKxUv6GvepzeBvpVJEz0YmqIx8aDeOf9p08mlqhHe9QTm/3zF3LpoPHADizVyv+edGpr3I27j9Ly9IzltL6+DaWf/QUWVlZtGzZkjVr1tChQ4eqT/LOMOUFX4owQfOuahGKlr3hs4urPrYhCYqAGbuUwg+KhKDaLQ958803895779GjRw/Wrl1LYWEhCxYsoKCggG7dujF16lSvLVIRqGjHO0VRiYOrZ/5JTkEJhpTccVY3Lh3e8ZTOeTTXxiWvLafEUV6/LSbBLWcmcO2YWjiRPhUJdre0rcIEcb3htIfgyAaVetbnCIhqC3fvU9n1wmLB0sD+CJoT0MlwakH28RLWpeRQVOKkqMTJko1pZWsMnwrXju6CxVSumDI3/MjXL99LVlYW55xzDps2bapewQOc9ZwaGSNcHxPk7ILfHvMfBQ+qccpMVotd1FLBSykZNmwYAMnJyYwePZpBgwZx99138/DDD3PJJZdw//33e0NqTRNg04Fj5BSUUFjixGY3mP9HyimfMy4qmJEJsZjd+p1mkyA8uJa+zGe/oOa8EaoOSVTSqa+u8pGC96QSJBw/qmL1o9poBd/ICBgl7zQkXycdZNZPO0nJqN2CBhEhFixutbV5WBBm06mPGqeN68qHt45keNcYgq0mwh3lzniTJ0+mVasa5GTufAbce0hlnusx5cS49oYmss2Jzj3CpObg55wFL7dXiTa+vQ3e6AW/PFa1M5GLv//979xyyy1l31NTU8nIyKhQZu/evfV2C5rGR2Gxg7kr9vL+r7vJrqVJvFWzkLJOu9kE7aJr1wn1hBCCZy4bwCvXDKZb60iCrSaGJ8Rw4aBarqMw9DaVcW7GDojqSI0cX72GCSLiT9xsDlKK/YWW8NZAyNgBH0+BN/vAhjkNL6amVgSMuf7lJdv5Zt0hiu0GoUFmPrtrDLGRNc+qtvFADi8t3o7VbOL/JvcmoVVkvcvocDi46667mDVrFt27dyc5Obl2J9j7Cyw4v2KymwbFZYovKV31zQTx/aHtUNg4t1yuyLZQlK2+W8Phwneh7xUez1hSUkJISAhSSs477zzi4+N5+OGHOXbsGBs2bGDx4sV069aNRx55hIgIneKyNgSSuf7W91exPTUXp4S4yGA+v3sMFnPNxyjfb0zjw9/3Et88lH9O6UNMLdqGBmPV67D0Qd85tZksgAkMVyIsYVXJrawhsHOJyq5nsqqOfn6a8hOwhsGNf0F8P9/I3IRpcnHyf+zMKJv/FgK2p+UypnvLGh/fv0ML5kz37jroFouFe++9l1mzZuFw1GFE3uVMuHUt/PE8bF6gQtlCmkNxARhuDUNpHHu9I90UPNB6gMp/nbpayVNKSX65wnfYVMrdqs4oJVJKrFYrixYtqrBv0KBBTJs2rT5vQNMIkVKy6eCxMoNQTkEJGfnFtG5e84Q0E/u3YWL/Nl6SsJ4YPgNaD4FfHoGDf6iolfBWriyT9REVcxKMSm1S74th6jxY+QrsXKy2SafqwJe2L8KsQuq0kvdbAsZcP7hzNMFlIS6Q6IWRuF8Q1xMmz4YB05SZvCi7ooKHhvHEDYpQK9OFNINOZ0Cbocp3wBoGY59Qf4Oi1N9el570dI3NqS4zv5gjub6yqDQthBB0i4/EYhaYBISHWIiN8MOReH3QYSRctQQ6nq70esERGkTBV8YSCmf8W8XGD7hBWeesYWpQMep+V/2OdNX/cQ0vnxeRUpKWU0hOgaeFgBofATOSf+C8XrSLDuNQdiFTh7Ynvha9/EbHvl9h01zfhdUIM8T2gm6uTHZmC1z3s+rRh8ao5Sm7n6/Wp243App5nqc0DIPnn38egKCgxuPMM2f5Xt79dQ8CuHhYe+6e2MPXIgU8r183lDnL91Jkd3LNaZ2xWgJmfHIiSW/BgRWA4RP9jrBAn8vUAlUAYdEwIxlyDyhTvTUUEs9V2e+6TPDZcrTeQErJY59vYlnyUQD+cX4vzhvY1sdSnRoBo+StFlPtQlcaM8W5J64EZbKqbR6XoaxnTBaY9BrYjqllKFv1Uw1Bi87lZWIS1acaZs6cyWOPPQbAfffd502J6w2nIXn7l91ljlz/W32A60/v0vApTpsYUaFW7jy7u6/FaBhsOSpFtTumIJWEpqEcbye9rhJx5R1SPjfWUIjuWr6/7RD1CTBSMgtYvuNoWWjkK98nayWvaUAMA765ETbNA0wqMYWzRJnSzn4J0tfDqlfLk2t4C2eJSq85d4Ia1QsTXPENrHhGTR+MfwY6jzvpaXr37o3JZMIwDNasWXPS8v6ASYDVbMLpSu0rEFhr4QCm0VRJ8XGYfy4c/FPVKXOQqmsx3ZTz6l//da0IWcuEO7VFOmH7l7DoNtWhj4iHC99XvgKWYDj3DYgNzA5XiNWMe/R0aJDZd8LUE1rJ+4g9e/awePHiKpdZDQ4OZuTIkRXXXd/9PWz7XDnICBPED4crv4WwGLW/z6Uw4Wn4/WlY9m/vNQZmK6T8BiWuUEVhVjH7hZlqtLHgfBUWFB5b5SkMwyAkJIQHH3yQZ599lp9++sk7stYzQgieurQfT3y5GYchefD8XoTVNjZao/HEqteVE6t0qrnwflfDOS9DsCuqpMNp6u+nl8KOhd6brmveUTn3ljrPHpcw7xzXdwEfjYf7Dnnn2j6mdfNQbhufyNs/7yI82MJ/Lu3va5FOGd06NTCtW7cmLi6OjIyMCquzeaJ///6sWLGiPHTMPXSuNEd1qYIHKMyGOePVXHhMNzWfV3hUmf/qC5NVjdQLM1F+m4aSxXasXCYhVIhNFUpeSsnUqVNZuHBh2bb+/VVlspU4+W5jGiaTYGK/1gRb/a8nfVr3liz9v/G+FkMTaNgLyxd9MpwQFF6u4EFNjc05C44fhvjBUHgEinJUNEt9YQmB899WVrnSVBX2QrfcGFJd33CWL1hTC7Lyi/lpazoxEcGM793KLx1urxzViStHdfK1GPWGVvINTHh4OL/99htPPvkk2dmeV6qTUrJ06VI2btzIt99+yxVXuGLMu52vUl4e2aQq2Dkvqe1Zu2HZv1QSmsxkQELWjpoLZQoqj409GaMegFH3qlGH+8qW7vkWLKEqCqAK1q5dW6bgJ0yYQKdOnXjyySeRUjL9g9XszTiOQMU2z5o2rOb3odE0ZobdDhs/VIo7OBJG3qu2H/hDmeoPrSxfhOpwLaa3hPnEdeE9F4RL/gcJZ8OGDypud1/4pu2IOin4ApuDq2f9SUGxA5MQbD6Yw98nVd1OaOoHreR9QK9evfj444+rLXP11Vczf/58Cgvd5tctwXDjn8rLNTxO9fQdJfD+KLVAjZTUyR3XsEPn8bDvlxOPD27uGmEYKinG0NtcxzjVqL50SsBwa0ScdmXS98D27du57LLLABg/fjxLly4t25dbWMKu9HwcrkmxjQdyKLY7/XI0r9HUO5Gt4e69kHsQotqpLHPH9sPcc1wr0J3CqLfNCEhbeeL2iDYuq5xUnvNdJ6jtsnRZatfytdJt6dk6knw4lxKHs8yp7act6VrJNwDaY8hPKTXR33TTTfTt25d//etf2O12MJmgRSel4AEKM5S5ThqUKWhTbWOIpZpjt3g47vxZat5/4sswfRM0a6+2D7gemnVQo/aQFuX5rIUJok+McpBS8u677zJ48GD27t1LQkIC//3vfyvec4iVqDArQigHt7iokLLlPTWaJoHZqupPaX3K2OY2anYpXnMtIzmkE46s97zv7r1w0UcqWua29aojDzDuCbXanCUMIlqXX9McXK2Vrjrax4TjdPUTrGZB99aBE3rnzwRMWttAY8eOHUycOJGUlJSybSNGjGDBggV07uwWqmY4YWZfFe4ihIpLv+gjWPse/P7vSmc1A1WY7UxWleiisGLOeO5NVYtSlF5rzVuQsRX6XwtthijzYUQ87P0Zfn4YwlvC5PehWXuklHzyySd8/vnnpKSksG7dOgCuvfZa3njjDSIjT0xYdCi7kLd+2oXJBNMndKtVVjNNRQIprW2TpSATXu+mnFzNQTDoJjjtAfjmJuWI605wlFpExhNhscp73+meOMsET7i1ByUF8OeLarpg+F1qZF9wRFkV1syEpLdVGuvz31LTCXVg44Ec5i7fR6tmIdw+oRvhIdqYXFdqWr+1kvdjSkpK2L17N9u3b+eee+7h0KFDREVFcfXVV5cpyJ49e3LNpRdi2jRXNQIDri/vjf+3ozLtlxLUTPXq7ccBAR3GQNpqZQWY9Br0vgxWvwkrnlbbzn5JzROWsvQhWP26Mt9bw+DWdRVCaQ4dOsTs2bPLphg2bNjADz/8ULY/MjKSWbNmcdVVV3nrkWnc0Eo+QDh2ALZ+ClHtVZIaIVSH+8nginPt4fGuGPtiwKTyzu/7WVnbLv8aYnvAL4/D5rnKanfFIug0pvz4OWfD/t/VdFtoCxUhE6zXi/BXtJIPMLKzs7npppv46quvTtg3Y8YMXnvttRMPmjUAjmw8cbswQ8excP3PKvYeWTNHmrcGQfp69mTD/oIQzpjxDhltzuH7778nNTWVF1988QRnwrCwMB555BF69uzJiBEjaN26dQ3vWHOqaCUfwEgJT4V7XqzKHKzy4J/9guoMCNOJybM88VR4eY6NoEiYtkLnpPdjmtwCNYFOdHQ0X3zxBV9//TU7dijP+e3btzNnzhxef/11nnvuOUJDK5m2J8+GeZNUGJ070qlSUoKa46+K0g6gq4GQiefy9ndb+PsSOzaHjVaL7iUvv4CiovKGZty4cZx99tkIIbBYLEyZMoWEhIRTuneNRlMJIeDi+fDl1Scmv3IWqxTTUH3nXcqKyr/jWJUy27CrUDr3DHeaRotW8o0IIQQXXXRR2feCggIWLVpEdnY2Q4cO5Z133iExMZHY2FgVf9pmEDx4BH59Av54ARyuxsASCiPuPvECqUlqZNB+FGyaD9/eDFJyrM9tHO1zJw+9sZWvvilPwHHkaCYAAwcOZMCAAYwePZobbrjBL2NfNZqAo+dF8PBx+Hgy7F3qWqJWqBS0Q6ZXLOt0qEx6QRGqXfjxQfjrZaXMJ70Kg26Ey76AVW+orJVDp5c792oaNdpc38jZsGEDl19+ednoHtQSrQsXLqRdO9fCMFKqTHlHtqjkOW2HQfsRFU/0w/2QNEuZ9tqfBnt/xuF0cO1X8PGW8mJRUVG88847DB48mEceeYSRI0dy1113YarOIqDxCdpc30RwlMCGDyHvoIp46TAG4twWTTIMmHuWK5ueAX2vgo1z3DJiCrj+V+g01hfSa+qInpNvQhQUFPDAAw/w5ZdfcuTIEQDuvPNOXn/99ZqdQEp4Mqh8PWlLCDhK+GKbwSX/U5tiIywMGnUmb731VkXvfo3fopW8BoDMnfD2wHKzvjlYzdW7L3Yz6n41h69pNOg5eR+yak8mi9al0r11FFeM6oTZ5F3zdXh4ODNnzmTmzJm8//773HTTTbzxxhusXr0aUHnwp0+fXp45Dzhy5AgPPvggycnJasNhUZ7rQhRDaAyrdylz/NX9BHNfvB/Oesar96HR+DtSShatT2XVnixGd4tjYv82vhbp5ITFVMxIGRGvYuDTXbHz5mAVeqsJSLSSr2d2HM7jwY/XU2w3WL7jKMdtdm6b0K3Brn/FFVfw/vvv89dff5UpeYDly5dz5ZVXcvXVV+NwOPjxxx+rTKurkm4oBd+mRTAP3XsLnPmk94X3IUfzbOQUlJDQKtLrnTJN4+WHTYd5acl2bHaDFTuOEhJkZlzPVr4Wq3rCYuCST+CHv6tY+ovmQlwvtQjNwT/V3H6vi30tpVc5kFWA05B0ig1vcj5DWsnXM9tTc8uST9rsBmtT6nFxmBoQFhbG8uXL2bx5M8XFxUgp+fPPP3nxxRfJyclh3rx5ZWXHjRvHI4884jEpDShHv969exMeHtgOOEs3H+Y/X2/BJAQJ8ZHMumEoFr18rMYD61NysNmVyctmN9h04Jj/K3mAHheqjztjHvKNLA3MrJ928slf+xECJvZrw0MX9va1SA2KVvL1zKBO0ahVxiHYaubMXg3fAJjNZgYMGFD2fcSIEdx+++38+OOP5ObmAiokb+LEiZjNOi/8mz/tpNiVT3vPkXw2HTzm+h01moqM7dmS7zenUWI3CLKYOK1b1cspa3yPw2kwd8W+sjXiF61PZfqERJqF1TI1cCNGK/l6pkNsOO/eNJxl24/QpVUEZ/hJLz8kJIQLL7zw5AWbIM3DgjhyzIYEnFISFep5cR2NZlS3OF66chAb9ucwuHM0A3Vn0K8xCUGw1UxRicoMaDIJgi1Na2CjlbwXSIyPJDG+brmdNQ3Pvy7uxz8+Xk/W8WKuGd2ZhFb6t9NUzZAuMQzpEuNrMTQ1wGQSvHDFQJ74cjOGIfnHBb0ICdJK3mdsOpDDN+sO0Sk2gstHdgyYedGft6aTtDeLUd3iGNO9pa/F0VSiY2w4n8wY7WsxAp5ftqazYmcGw7rENA6v9BrgNCRfrD5ASkYB5w1sQ+92zX0tkqYSQ7rEsOj+cb4Ww2f4jZI/kFnAXXOSsNkNgi0mMvJtAbHW8NLNh3lq4RZsdoMlG9N45rIBjEqM87VYGk2DsmLHUf791WZsdoNftqYDBISif3PpTr5Yc4BiV/2eO30k7WMC21FV07jwm6HyjsN5mFyhDcUOg6S9VYV3NS5W78kq88Ytthus3xcY96XR1IaN+yt6pa8NkHqwancmxa77MglITqtiqVeNxkf4jZLv3a55Wb6GEKuZ03sEhll7ZGIswVb1mIOtJoZ01XN5mqbHsIRYgi2qHoRYTYzuHhjWrNO6xRHiqt+GhF5tm/lYIo2mIn5jrm/TIpR3bx7O0s3pdIgN49wAMOUBnNk7HovZxLqUbEYkxDK8qw650TQ9hnaJ4aWrBrF6TxYDOrUImCmr28Yn0qZFKPszC5nUvzVto8N8LZJGUwG/UfIACa0iA9Kz+fQeLb1qmTiSW8S8P1IItpi4ZnTnJhUDqmk8BKJXuskkmDKkvVevkZyWx1drDtKmRShXjuqE1eI3BlhNI8CvlLym9jicBje+u4rs48WYTILVe7KYM32Ur8XSaDT1wNFcG9Nnr6bI7iTYYuJgdiGPTunja7E0jQjdJWzkZB8vIb/IjiHB4ZTsOpKPYdR8ZUGNRuO/7D6Sj8lU7pC8dl+WjyXSNDb0SN7PyS+yM/OnXWTk2bh2TGf6dWhRYX90RBDREcEczbNhEtCjTbOyRkGj0fg3aTmFzPppF4aUTJ/QjXaV5vS7t44CpCtNtonTugWGL4Om4dBK3s959H8bWZeSjd0pSdqXzed3jyE2Mrhsv8VsYvYtI/hi9QGCLSYuHtbBh9JqNJqaIqXk1vdXk3m8GAFs2J/Dt/eNq9BJj4kMZvYtI1m8PpU2LUK5YFA73wmsaZRoJe/n7EzPx+5U5nezSXAwq6CCkgdoER7ETWck+EI8jUZTR2x2J1nHi5FSLe6cW2inoNhBZKW1EzrGhnP7WQ23XLUmsNBz8n7OhN7xhFjNBFlMBFtNdGsd5WuRNBpNPRAaZKFPu+aEWE2EWE10bx1FRIged2nqF/1G+Tl/n9SD/h1bkH28mPF94gkP1j+ZRhMovH7dEL7fdBgpJRP7t0EI7U+jqV+0xvBzTCbBhD7xvhZDo9F4gWCrmcmD9Ty7xntoc71Go9FoNAGKVvIajR6+phEAACAASURBVEaj0QQoWslrNC4MQyKlTiSk0QQiziZav/WcvEYDfJ10kBeXbMckBI9N6cOEvq19LZJGo6kHpJS8tCSZL9ccICLEyivXDG5SqwXqkbwmYKlpz72g2MFLS7bjcEpKHAb//nqLTg2s0fg5zhrW0W2puSxan4ohIa/IzpNfbfayZP5FoxrJSylZtD6VpH3ZjOkex4Q+erSlOZHa9twNQyKr+a5pGBxOg3l/pLA/4zhThranf6UUzhoNQInD4L7560jam0Xb6DBm3jCUllEhVZa3OyXukYmlycWaCo1qJL9kQxovLdnOD5sO85+vt/DHzgxfi6TxQ7an5dWq5x4ZauX6MV2wmgVWs+Cuc7pj1vn/G5xXvk/mg2V7+G7TYe6ek8SBrAJfi6TxQ77fmMbmgzlI4HBOIbOW7qy2fL/2zRnWNQarWRBiNfHA+T0bRlA/oVGN5JP2ZWGzGwDY7AabDhyr84INRSUOXly8nR2H87loSDud870Kthw8xv0L1lFQ7GTa2C7cMLarr0U6KXanUeue+01nJHDp8A6YTYKIEOtJy2vqn6R92RQ7VP02C8Gu9Hw6xITX6VxH82w8+81WsgtKuPXMBEYm6oVdPPH9xjSe/XYbJgH/vKgPZ/Ty/5wcdqdB6SycAZQ4jWrLm0yC5y4fSNbxYsKDLIQEmb0vpB/RqEby43q2IsSqRA62mhiREFPnc736/Q6Wbkln95F8Xv9xJ2v3ZdeXmAHFPz/fyLFCO3anwYe/720Uo6u+7Sr23B88v1eNjmsWFqQVvA8Z17MlIVYTApXLvU+7ujtH/ePj9azcnUlyWh7/9+kGMvJs9SZnoGCzO3lq4VZsdieFJU4e/2Jzjee5fcnE/m1oFx1GkMVEVKiVW89MrNFxMRHBTU7BQyMbyY/t2YpnLx/IpgM5DOsay4COdZ+z25txnBJHaQ9Qcii7kMGdo+tH0ACi1HICIAQU26vvNdvsTv71xWbW789mZGIsj0zug8XcsH3Jpt5zb6zcemYiHWMjSM0uZHyfeFo1C63zuQ7lFFKqr0xCcDTPRlw187ZNkcqOqeXfq56qysiz8fBnG0nNLuSS4R2Y5gPLXniwhbnTR5FdUEKzUCtWS6MaqzY4je7pjEiI5ZYzE09JwQNcNrwDwVYTYUFmgixmRiXG1pOEgcV9k3oQZDERZFFrWSe0iqi2/LwV+/hjVwbHCu38svUIX6891ECSnkhT7bk3VoQQTOrfhpvOSKBzXPXv2cm4aHB7Qq1mQoPMxEWFkBivF3aqTHiwhWtGd8ZqNmE1C24+I+GkHfKnv9nKtkPHyC4oYc7yfWzYn9NA0lbEZBLERgZrBV8DGtVIvq4cyS3ihUXbySuyc/tZ3RjQsQXj+7SmXUw4+zMLGNw5mpiI4JOfqAkyoW9rhiXEUljsoFWzkJMuoJGZX4zdZSGxOw2y8osbQkxNE2Z7ai6v/bCDIIuJ+8/rSfuYcKZPSGR4QgzHCu2MSowlSCsDj9w6PpGLh3VACGrUBmbmF+Mss5BAdoGu3/5Ok3jz7523jj93ZbDp4DHumbuW3MISALq3juLsvq21gj8JUaFW4puH1miFrEuHdyA0yEx4sIXwYAsXDGrbABJqmirFdid3fpTE+v05rN6bxYyPkgBlFRjcOYbxveMJDWoSY5k6ExsZXOM28OYzEsosoDGRwYzoqi2g/k6TePtT3ebnhFC90WZhQb4VKkDp2iqSL+85nT93ZWAyCb00rsar5BYpp1AAKeFIng3DkJh0CKRXOL1HSz65czQrd2fSIjxIh5o2AppECzypfxu+33QYJLRuHkrH2LqF5WhqxqaDx3hu0TbMQhBsNTP/9lFEa2uJxgvERQbTLT6SPUePA3BaYpxW8F5myYY05q7Yh0lA2+gwPvh/9u47PKoqfeD4905Jr6SHEEINNZTQkS5NQHBFFBREyoqKim1ZUVdF9qcuimIFBRHWVVCkqXSV3kM3hAAJoaSSXidT7u+PkwoBEkgyKefzPHmYzC1zRnPue+8p7/l7j2ofXCuVX70I8v8Y2YY+wd5kGUz0CfaSf5BV7Lu90UWj8C0q7I1MYlRnuWa2VPkUReGLJ7qxMyIBW532jvNmSOW38sBF8oxmAK6k5HAuPpPW9SgXfG1TL4K8oij0kpW/2gR6OHLmanpREho/tzufCiVJt2Oj0zBYpriuNr6u9mTlZaKqIgW0h7NspavJ6kWQrw0iYjN4e81JDCYLL9/XulbflLwwrBU5BhPn4jMZ06URXZreedIiSaoLdkUk8tGmCBxstLz1YAgtfJ2tXaQ79v4jnZi37hSp2fk8dW/LW+aNl6xPqcj6ul26dFGPHDlShcWpv0bM/5PkLDHq31anYeMrA3C0k/dg0p1TFCVMVdUu5d1f1u+qkZ6Tz6gPdxYl3/JxtWP9i/2sXCqptitv/Zad01UsOdPAxaSs2y5dmpZjLHqtApl5xpvvLElSjRCbmktsau4t90nPNZbKIZeWnV+1hZKkEuSjYhXaejKOeetPo1GgY+MGLHi0801H/o7v2ZjVhy6jKNCpsTs+rrIJTJJqsi+2RbLyQAwA47oHMnNIcJn7NWrgQIdAd05dSUNVVSb0CqrGUkr1nQzyVeiTrWeLmuhOXErlTGw6bQPcytx35pBg7m3nh8Fkpn2AW7kSz0iSZB15RjP/23exaEGXH/bHMK1/8zLTKCuKwkcTQzl1OQ0HGy0t/WSKXan6yCBfhRxtdVwrSOtqsai3TQzTyl9WfkmqDXQaBa1GKQryWo2CTnvzG3OtRrnr9TYk6U7IPvkqNO+hEHxd7bC30TK1fzOC7nLRDan8fj50iSeXHuSLbZGYbrPetCRVlE6rYd5DIbjY63Gx1zNvbIjMv1FNTGYLX2yL5MmlB/n50CVrF6fGk0/yVaiFrwvryhhFm5dvJi4tFz83e7lKWhXYG5nEp1sjyTOaiYjLwE6vZUr/6l8SU6rb+rbyYes/fW54PzPXyLUsA40aOMjAXwWW745i1cEYDEYLZ+My8XOzr9VTjquaDPLVLD4tlye+OkCe0YydXsuyv/fAVyaLqVQXEjKL8pmLC0GGlUsk1RcnLqUy679hqCo0bGDP0mk95I18JYuIzSjKqGkyW4hKzJJB/hbkbWY1++ngJdJz8snNN5Oek89PB2VzU2XrE+yNjVaDrU6DrV7DSLkSnlRNvtgWSW6+mTyjmdjUXHadTbR2keqcUZ0DsNWL+q3XaugdLAP8rcgn+WrmZKdDq1GwmFV0GgWnOpDwxmxR+W5PNCcupzKknR/DOvhbtTxNvJ1Y/lRPwqJSaOnnfNMZDZJU2Zzt9GgUila9rAurMOYYTCz+4zxxaTmM7xlEp6AGVi1P31befDG5K5FxmYQ2bUCgh1xw7FZq/19gLfNIz8aERadw8nIaIY3ceKRnY2sX6a59tzeaZbsukGe0cDQ6hQZOtnRrZt1UtoEejrLyS9Xu5RGtefG7HK6m5jK0vR+9WtT+9dbfWXeavZFJ5JssHLqQwg8ze1t9PYq2AW7y5r2cZJCvZvY2Oj6b3NXaxahUJy+lkVfUR6ZyLj7D6kFekqzB182e72feY+1iVKrwK+lF+T60GoVL17KtHuSl8pN98tJdGxbih51eg06roNNq6Nas9j+9SJIkDG7vi51ei16roNMoMp9HLSOf5KW7Nri9H+6ONpyNy6B7c0+a+9TeFbYkSSrtmcEtad3QlcT0PAa188XVwcbaRZIqQAZ5qVJ0aeohl5SVpDpIURQGtfW1djGkOySb6yVJkiSpjpJBXpIkSZLqKBnkJakabNu2jfHjxxMUFISiKLz11ls37HP48GGeeOIJmjdvjoODA8HBwbz99tvk5eVVf4ElSaqQ9evX0759e+zs7GjTpg2rVq26YZ/09HSeeOIJ3N3dcXV15dFHHyU5OblKyyWDvCRVg82bN3Py5EkGDRqEg4NDmfusWrWKCxcuMHv2bDZu3MgzzzzDggULePTRR6u5tJIkVcSePXt48MEHGTBgAJs2bWLEiBGMHz+erVu3ltpv3Lhx7NixgyVLlvDtt99y+PBhxowZU7WFU1W13D+hoaGqJEkVZzabi157eHiob7755g37JCUl3fDe4sWLVUC9ePFihT8TOKLK+i1JVW7IkCHqgAEDSr03fPhwtXfv3kW/79u3TwXUnTt3Fr138OBBFVC3bdtW4c8sb/2WT/KSVA00mttXNU/PG/MLdOrUCYDY2Nii9/bs2UOfPn1wcXHBxcWFjh078tNPP1VeYSVJKjeDwcCff/7JuHHjSr3/yCOPsH//ftLT0wHYtGkTPj4+9O3bt2ifbt260aRJEzZt2lT03oYNGwgNDcXR0RF3d3e6d+/Ozp0777h8cgqdJNVg+/fvR6PR0KyZWCo3IyODkSNHMnr0aP71r3+hqiqnTp0iLS3NyiWVpPrpwoULGI1GWrVqVer91q1bY7FYiIyMpGvXrkRERNywT+F+ERERRecaO3Yszz//PPPnzycvL4+wsDBSUlLuuHwyyEtSDRUfH8+8efOYOHEi3t7eAERGRpKens5nn32Gs7NIOjRkyBBrFlOS6rXU1FQA3NxK59J3d3cvtT01NfWGfQr3i4qKAuDYsWM4Ozszf/78ou333XffXZVPNtdLUg2Un5/PuHHjcHJy4qOPPip6v1mzZjg5OTFhwgTWr18vn+AlqQ5p37496enpPP7442zdupXs7Oy7PqcM8pJUw6iqyqRJk/jrr7/YuHFj0RMBiLv+bdu2YTQaGTduHF5eXowYMaLoSUCSpOpVWD8L+94LFT7BF253d3e/YZ/C/Qr3CQ4OZv369URFRXHffffh6enJhAkTSEpKuuPyySAvSTXMrFmzWL9+PevXry+zD69Hjx5s3ryZtLQ01qxZQ2RkJBMmTLBCSSVJatasGXq9vqhfvVBERAQajYaWLVsC0KpVqxv2KdyvZD0fMWIEu3fvJjk5maVLl7J9+3aeffbZOy6fDPKSVIO8++67fPbZZ3z33Xfcc8+tlyy1t7dn1KhRTJkyhfDw8GoqoSRJJdna2jJgwIAbZrisWrWKnj174urqCsDw4cOJj49nz549RfscOXKEqKgohg8ffsN5XV1dmTBhAg888MBd1W858E6SqsCKFSuYMmUKFy5coHHjxsTExHD48GFA9LeHh4ezevVqHB0diyr4999/z5w5c5g8eTINGzbkwIEDRedr1qwZXl5e/Pbbb3zzzTeMGTOGwMBArl69yuLFixk4cKBVvqck1UfX1+833niD/v37M2vWLMaMGcPGjRvZuHEjmzdvLjqmZ8+eDBkyhEmTJvHBBx+g0WiYPXs299xzD/feey8AixcvZv/+/QwbNgx/f3/OnTvHTz/9xKRJk+68sOWZTK/KZBmSVCHLli1TATU6OrrU79f/NG7cuOiYxx9/vMx9AHXZsmWqqqpqRESE+uCDD6oBAQGqjY2N2rBhQ/XJJ59Uk5OTbygDMhmOJFWJ6+u3qqrq2rVr1bZt26o2NjZqcHCw+sMPP9xwXGpqqjp58mTV1dVVdXZ2VsePH18qCda+ffvU++67T/Xz81NtbW3VoKAg9R//+Ieal5d3w7nKW78VsW/5dOnSRT1y5Mid31FIklRtFEUJU1W1S3n3l/VbkmqP8tbvCgV5RVGSgJi7KZgkSdWmsaqqXuXdWdZvSapVylW/KxTkJUmSJEmqPSo08M7T01MNCgqqoqJIklSZwsLCrlXkSV7Wb0mqPcpbvysU5IOCgpB9dpJUOyiKUqGmd1m/Jan2KG/9lvPkJUmSJKmOkkFekiRJkuooGeQlSZIkqY6SQV6SJEmS6igZ5CVJkiSpjpJBXpIkSZLqKBnkJUmSJKmOkkFekiRJkuooGeQlSZIkqY6SQV6SJEmS6igZ5CVJkiSpjpJBXpIkSZLqqAotUCNVLYPRzLojV8jMMzI6NAAvFztrF0mSpEqSmp3P2sOXsdFp+FvXRjjYysuvVPXkX1kNMufHExyOSsZsUVlz5DJrZvXFTq+1drEkSbpLJrOFqV8dIDEjD40CuyIS+Wpad2sXS6oHZHN9DXIkOpl8kwWzRSUv38yVlBxrF0mSpEqQkpVPcpYBk0Ul36xy6nIaFotq7WJJ9YAM8jVI24au6LUKCqDTavB3s7d2kSRJqgQNnGxwttOjUUCnVWju64xGo1i7WFI9IJvra5D5EzqzfFcUmXlGxvcKkn12klRH6LQalkzvzn/3RGOr1/J4nybWLpJUT8goUoM42up4enBLaxdDkqQq4Otmzysj21i7GFI9I5vrJUmSJKmOkkFekiRJkuooGeQlSZIkqY6SQV6SJEmS6igZ5CVJkiSpjpKj66V6J8dg4o/wBOz0Wga08UEr5ytLUp2RlJHH3sgk/Nzt6d7M09rFsToZ5KV6xWS2MG3JAWJTcwGFXREJzB3bwdrFkiSpEqRm5/PYF/vIM5lRUHhyYHPG9wqydrGsSjbXS/VKbFousal55Bkt5BnN/BmeYO0iSZJUSY7FpGA0WzAU1O/1YVesXSSrk0Feqlc8nWzRFvzVaxRo5OFg3QJJklRpgjydsKhiTQC9VkOwv4uVS2R9srleqharD8bw48FLNPFy4rUx7XCx11ulHA62Oj6f3JUvt5/D0U7HrKGtrFIOSaorzBaVT7eeZW9kEt2aevDC8FbotNZ5fmzq7cTcsR1Yuf8igR6OPDc02CrlqElkkJeq3MlLqXy27Rx5RjOxabn855dw5o2zXj94K39XFk7qAsDFpCzOxWfS3McJRZED8CSpojaEXWHdkcvkGS0kpufRsIEDE6zYD963lTd9W3ljsahExmfiZKcjoEH9bbGTQV6qcvHpeRTGT5NZ5XJKtnULVOCLbZGsOhCDoigMbOPDv/7W3tpFkqRa50pKDnlGCwAGk4UrydZfIttiUXnxf0c5EZOKRVV5+t6WPNyzsbWLZRWyT16qct2beeBgo8XBRoudXsNjva2/ApfZovLd3osYTGKAzrbTcaRm51u7WJJU69zX0R97Gy2Otlrs9VruD21o7SIRnZTF8ZgUco1mDCYLX+84b+0iWY18kpeqnKuDDStn3sOxmFQautvTzMfZ2kVCo4C9jZZsgwkARVGw08t7XkmqqGY+zqyaeQ/hsekE+7ng52Zv7SLhbKfHohb/7mJnnTFANUGtu6olZuSxYncUvxy9grnk/0WpRnO219O3lXeNCPAggvoHEzrh42qHh5Mt8x4Kwd5G3vNa2/mETJbtvMCuiERrF0WqAG9XO/q39qkRAR5EeV4Z0Rp3RxsaNXDgvUc6WrtIVlOrrmrZeSYmfbmPrDwTOq3CiUtpvD6mnbWLJdVSnYIasP7FftYuhlTgYlIW074+SL7JjI1Oy8whLRnbLdDaxZJqqVGdAxjVOcDaxbC6WvUkfz4xE6PZgsmikme0sFve7UtSnREWnYKqqlhUyDOa2X463tpFkqRar1YF+UAPRwryHKDXamgb4GrdAkmSVGlaN3QtmoVhp9fQOcjdugWSpDqgVjXXuzva8OWUbny/9yIezjZM7d/c2kWSpDJFxmWw+2wizXyc6d/ax9rFqRXaNHTl/8Z15NfjV2nt72rVudaSdCsHL1zj9OU0ujT1oENgzb4ZrVVBHiDYz4W3x4ZYuxiSdFPRiVn8fekhDEYztnotMwfnMbZ7/ZyjW1G9WnrRq6WXtYshSTe180wCb/58EoPRwoo90Syc2IWOjWtuoK9VzfWSVBuEXRR9yyqib/kPuQiOJNUZO84kkGe0oAIGo4UD565Zu0i3JIO8JFWy1v4uUKJvObRJA+sWSJKkStM5qEFRTg07vYZ2jWr22LBa11wvSTVd2wA33nu4IxuPx9K6oSsP95BN9ZJUV4zs1BCzReVIdAr9WnlzT7C3tYt0SzLIS1UuNzeXTz/9lOjo6Nvu6+7uzvPPP4+PT+0erNazhRc9W8i+ZUmqaxRFYUyXRozp0sjaRSkXGeSlKmEwGPjxxx+Ji4tj+fLlhIeHl/vYb775hqeeegpfX1/Gjh2Lh4dHFZZUkiSp7pJBXqp0586dY/z48YSFhRW917x5c2bMmIGDQxlLPqoqxOzGHHecH47nsu9UDG+99RYA//73v9my6yAn4/MJ8nSke3PPavoWkiRVCrMRdrwFsWHQeSq0faj09qtH4PJeCLwH/EOtUsS6TAb5WkZVVZbuuMD20/GEBLrx8og22OhqzvjJHTt2MHLkSLKzswkICGD06NEEBAQwc+ZMnJycyj7or59g3Qawz+GpFvYsHfkof2V78Mknn3D58mWGT34Zr05DcWjgx7NDg2WqU6nOMhjNfPDbGU5dTmNoiB+T+zZFKcwQVFv9/hoc+gxMuXBpN7gEQKOeYtvFnfC/+8BiBkUDj22GoL7WLW8dI4N8LfNHeALf7b1IntFMbFouHk62PDmohbWLBemX4fc5zP3XVrKzs+nevTtbPpyGa+w2aBICl7ZCbjIEj4bw1ZAaBZ2mgHcbiD0KRrEGtdacy9+72cCYhSiKwsKFC4nZ+T0xO7/HKaANKzXvMLZLQ7iwFTQ6aDIINDXnJkeS7sbXf55ny6k48k0Wlu+Opqm3E/1qQjKl2KOw6x1w8IRB74K9O+xfIJ7O240HQzooCjQfDmFfQX4W9JgFTt5w5YAI8CBa7eJPFAf5v34qqvuAuDb4dYao7eDsBwHdq/+71jEyyNcyV1NyMJotAOSbLMRcy7ZKOdasWcOzzz5LXFxcwTtqUcphgI+eH4PrjudFBT6zBtCIoLz5BTDlgWqG/R/C+F8hM07cxSsa0Oih3SMAvP3221xJTOG3Lb9jSE8i60o4P7/+IJo3YHAzLUv/ZktA19Ew9vtq//6SVBUuXssm3yTqt9li4WpqrpVLBOSmwrf9IT9T1M+kcGg6BPb9R9Tv8J9AYwMarajD+VmACnv/A0+eEIFd0YCiFfs0vbf43A27wnEHcR69A/iEwOJOkJUgrhED5kKvl6z1zesEGeRrmYFtfVm+OxoVFYtF5cFu1TvCMzc3lxdeeIHFixeXud1OBy/20tLD5WrxHbrFVPBv/o0HrHoALMbi33u+BM2HAODq6srq71ewKyKR7/44yZGVH3B8z1ZUVWXreTNNP8ihqfsPdPjRyMcLP8HPz68yv6okVbuHugdyJCoZjaKgUZSakRI5Lab4tcUICSfFDXth/VYtYM4D83XHqWb4qlOJ+q3A6G/Bo0Q68g6TxE3EuY3QciS4NxUBPj9TbN//kQzyd0lR1fKvyd6lSxf1yJEjVVicmuuHfRf59dhVWvm78MqINtjZaK1WlqSMPE5dTqO5jzOBno7V+tnz5s3jjTfeQFEUFixYwLPPPiv6DFcMgcv7QFXReLWE4Z/Ad8PBZBCJYVQVKMffWsPuMHWvuOMvgyU/j8Q3PZmyOptN54vf93LSsvy5Pgz/1y9ge5O+/3pGUZQwVVW7lHf/+lq/TWYLn2w5y5HoFPq39mb6gOZW7Qe/mJRFVFIWIY3c8XS2tVo5ihjz4LNgyE4UT+Ot/wYBPWDbP8CYC1jKf65OU2H0kptvTz4PX4YUN+97t4dGveDiDmg1WnQVyO45oPz1Wwb5cjhw/hr/XHmcPKMZG52GMaEBvHhfa2sXq9olJibSvn17EhMTeeONN5g7d27xRpMBTn4nRtKGPCYC7aW9EP0HeLaBdZNK9L0pgApaG7BYQDWV/iAHL3h0IzQs4+83JwU2TEc9s4aLaRCXreVff6r8HiUuNC/01PDuY52xnfgLOPtWyX+H2kIG+fJZsTuKpTsuYDBZsNNrmD2qLcM7+Fu7WDVLTjKc+gHs3KD9eHETfmYdJJ4Gz1bw0zhuuIm3cRZdcyVb6kDsP3EruF7XCqmqkHMNlvSG1HPiPUUnWg3MeeIGQ6sX/f4Pfg96uyr7urVBeet3nbkliozLYP6v4fxv70VM5grcWZbDlZQcCm+G8k0WohKzKvX8tcHWrVsJCQkhMTGRBg0aMGPGjNI76GzF9JiuM4qfpAN7Q/fnRBDX2hTvq2hAaysqb6OeoLMvfa6cJDHitiSLBZbfC/O9IWItigJN3KFXoIatEzW8Owh0Gvhov4We7xzh7DdPVP5/BMlqDpy/xvu//MXmE7FU5MGkPKKTsjAU9IMbjBYuJ1tnnEuN5uAB3WdCh8eKW9laj4HQ6ZCVSOlQooj+dYsRAvuIel7StbOwdlLp9/Iy4JOW8KF/cYAHMZjPnCdeq2Zx03B+Exz+vLK/YZ1VJ4J8QnouTy49xM+HL/PVH+f44LczlXr+PsFe2Og0ONhosdNreLhn3UxTqqoqGblGLBZxEY2KiuLPP//kueeeY+jQoSQkJNCvXz9OnDiBv/9tnnTObxF35O97wOpHIC+tYIO2oA/PIJ7srxyAx/8E7XV35bkpcOxbiDsufl/3OET/Lip64ROD3gF0dmj0dvyzr549T0BTdzgWDyH/+J1la7dV1n8ayYqOXkxh9spjrD1yhfd++YsNR69W6vlHhzbCTl9Qv220DG5XN8d2mMwWMnONlXOTFPY1fBECH/jBpmco6pDX2okbemOOCMgJx+HhNWLAXhEVUi7A8eWQGi2e4Jf0gNTzxeN3FC3oHcVo/sIHgqIvYhCDeeNP3P33qAfqxMC7yPjMom4ag8nC4ajkSj2/j6s9K2few9GYFJp4OdHcx7lSz18TpOfkM33JQS7Hp+BmYyQ48yCffPRh0QVBq9Xy1ltv8eqrr6LV3mY8QmI4/HA/mMsYaNegGWReBWPB05JqFk/63u0grkRTsQr8+pS4i/duJy4KJTn5wsB5kHYR9n0IGi3dAxW+fqoD9y9NIjvhIm/M/5KWbTvSWy5dWqudiEnFWPCknWe0cOD8NUaHBlTa+Ts2dmfFjF6cjc+gXYAbfm72tz+ololKzOKpbw6RbTDRIdCNjyd2QX+n+TXC18BvTxcH5JKaDxHTWwuZybPTAAAAIABJREFUjeAdAjaOJW70ETNq1k8XdT/wHkg+V/o8jXpC52kQ+Ruc+w0sqrhRUDTiAeHyfljaG54MA8/gO/se9USdCPLBfi5F07dsdRp6tqj8rGgezrZ19g4f4Ie9URxct5TLO/+HajGxueD9Ll264OPjw5w5c+jVSAMrBoGtMwz/FNyDyj5Z3NGyA7xGB9kJoLcX2y1G8VT/3TBReUsxg7ng6SDx9I3bRy2B4BHwH6/iQTo2TiQETcGz4wmytywiPzebPWcTZZCv5To3aYB+twaDUfSZ31MF/z8DPR2rfRBrdfp4cwQZuUZUIDw2gx0RCTdez/76Scx99wgWA2ftXMo+WeRvZQd4jR4u7gIbV/G0jQr52bCsj2iOL6nkOJxLuylathFEXX/gv2DfADZMK/1079FCTOErbM27tEcG+duoE0He28WOJdN78OuxqzR0t681CwfUBAsWLGDevHmkpaejWsTTks7eBR8/f75b+iX9+/cXOxoy4cOGBVNbNOLO+9mI0ie7chCOLoHk6566C1lMImnG9Uz5Nw6+u55aYpxFk0EiwAM4eotBQahgMdOkTRfsHKMASDq+lYyI3TCq7a3PLdVoHQLdWfBoZ3afTSKkkRsD29bvAZV34vq5Asr17yScgnWTRTN73FHR1P7QytL7RKwXyWrijpX9IRYjGNKufxMyLpejhIVdCArc80/xAGE2FgzOLbg26B0geIxovTPmiGP8yz2utN6qE0EeoKm3E88NlXd0FREREcFLLxXPQbV38yJo5Czad+vL4indcHMsMViuMDkFABaRsa6kpAhYPrB09qryKmv+/K0kR4p/o/4Q5VAUMQp3xOf06NSFD+d48krscc4c2MYHrz/PrMkP4uUln+Zrs9AmHoQ2kQsV3akXhrfi6WWHScvJp0OgO/1bX7c8avI58aQMopUt4WTp7Wd/gdXji1vNqoxa3Nce9nVBgFfAxgke2ySm7jl4QPxx6DgZfDtUcXlqvzoT5KWKyc3NZeXK0nfqxw7spnGT5tjqNTfOE3ZvAh4tCy4GCrR+sPT2q4egkkc931RWAkRsgF3zxBMHiLt8GzFWYkRoEPft24KHhwepqamkpKTIIC/Va0FeTvz2Sv+CaYJljKkJ6idmuRS2mHV9uvT2qO3VEOBLfNa1SNj+z+JuP9UsptZqtNDrxeopRx0hg3w9NWXKlFJBvn379gQGBt48yY9GC1P2QsQ6cVfdcmTp7QE9KFeym8pgMYo7efsGiAkiFnGDYecm+gQv70UJGoCXlxepqanVUyZJquEURSk7wIN4On76lJie5tbkxkVimg6Gw1/eOOe9KmhtRb+7rXNx5jvVIq474T9DynmRkMejBqzZUQvIIF9P7d+/H4BXX32Vbt26MXToUOztbzOq2MYBQiaUvc2zJQT1h/Oby95emTR6kR+7YTdIjxGL43SeJgb7rBwt/tXZgkk270pSuTl5Q8fHy94WPBKcfCDjStWXQ7VA/DHRHH/8W1HXB8+H48tg97tidP2uf8Mzf92YUEe6gQzy9dyoUaPo2bPn3Z/IkAUxu0q8UdjcXwVP9xYjHPxEdBt4tIQ5meL1+qnFYwKMOZBfvzNiSVKlSbkAmbHFvyua0oNhK5MxC3b9H+hsoM1YeGC5eP+LkOKptyAyarZ/pGrKUIfUiWQ4UsUFB4tBiiNGjODQoUN3f8KEE9dNcytnrvo7ooq7eVMeXIsQiXMAGvUWCTSgKFGOJEmV4MLW0gltqirAF53fJG7Uz24ofi/wnuLsmKpZDrorJ6sHeZPZwpGoZE5fTqv0dJXSzS1fvpx27dqRmprKW2+9dfcndG9WTQPvlIKfgqVpHTxFXzxApydgyHxoNQbu+1z04UlWlWMwsf9cUr1MBV2n+ITcdNGoyqWlqBVQawN+ocWbhn0EvV4Wg37HbwCv+rd+yJ2wanO9qqq88F0Yp6+ko6owpksAs4a1smaRrC46KYsvtkWi02p4dkgw/u5Vk33L19eXzz//nH79+rFp0yZ8fX1p0aIFS5cupWXLlhU/obMvTNwCqx4UCW+qgkew6DP07wqnV4LFDAPeKr74KAp0fUr8APBu1ZRDKpccg4nHvtxHWnY+ZlVl9sg23NexobWLZVWHo5L57+5o/NzteHZIME52+tsfVBME9obR38C6J6pulH3zEWLAn29H0f/u5Av93yrerrOFgXNverhUNqs+ycel5XLyUhq5+WbyjGZWH7pkzeJYnclsYcbSQ+w5m8SOMwk8/W0lNKPfQp8+fZg+fToACQkJ7Nmzh6effvo2R91CYG8Ys0yMjq0KGZch9O/Q7F6xXOUDy0QT4vej4KuucK4aBv1J5XYkOoW07Hxy8s0YjBZW7I62dpGsKjY1l1e+P8qhqGQ2Ho/lzZ9PWbtIFdPuYej3RunFpipTWrSYutd8CIz9QTy5p0bDN31hWT+RsEeqMKsGeRf70nex7g5V9MdTS6TnGsnJN4vebBUS0vIqfUW9khRF4auvviq1otz48ePv7qQthov14IcugIfXwT+uwaiv77CA1zU0GXPEKlWHFxW/t+pvcG4TxB6BHx+EjMpdvES6c94utlgK1z7QKHUyJ3xFXE7JRqsRTdFGs8q5+IzbHFED9XkVJvwGg/8Dk/6A2anQftLtjyuLzqH079fOiFUmo/8Uv5tNIsHWpd1iUO+3A8RqlFKFWDXIO9npeX98Jxp7OtLKz4WPJobe/qA6rIGjDc19nLDTa7DTa+je3AOdtur/Fw0ePLjo9aJFizh//vzdndA/FHq+AK1Hi/m37R4Ra0BfH7QBHG+xHoDeAbo8VXoAnTkfNs4s/j3lfIlMfIqYTgdER0cTGRl5d99Duiut/F2ZWdDl1DnIndfHtLN2kayqbUNXbHVabHUa7PTa2rtmfbN7ofcr0HQA2LnCiM/ALag4Y14hRQfaW9zY+bQTKaqLBvSpoitgTcFNgzG7eJ48QF5qcfIrqdyUigx269Kli3rkyJHb7yjdsbx8M9tOx6HTahjczrdagjzAvn37mDBhAjExMTg5OfHFF18wceLEuztpfjZ8OxDiwkQTvq0rZMdz01H3Gl3phS9snGFOBmTGw4fX3QzMTgF7d9GMVzR1T4F247kQ9judF6aQkWskODiYU6dOodfXkr7PSqQoSpiqquVO7i3rd9VLzjKwIzwBb1c77mnpdWNmydok7RJ8c49oPbN1Ec34OdeAkk/bCjet776dYMZROLoMNkwpcYgO3ixIuvMfH8hJFK+1ttD0XpEIK+QxuPddMQ6nnipv/bb66HqpNDsbLaM6BzC8g3+1BXiAXr16cfz4ccaNG0dWVhaTJk1i1qxZd3fS48tFgFfNYMqB7Lib7KgVAd7Bq3QTXn4mvGMHSWdKT9/R6Iuf7nNLLIihtYEzq/n1WAIZuUYCvV3Yt29fvQzwUs3k4WTLg90C6RPsXbsDPMDvcwoWn7GIhWlyEikd4AsoGlFf/bqUnmYbfwze8xADaku2Ajj5FL82lOjSsJjhwhaxVPWhz0T2Tem2akyQj4zLYO6aU3y5PZK8fPPtD5AqnZubGytXrmTJkiUALFy4kMzMTFRVLfqpEGNOiab0QqpYirLUBwdCn9fgyaM3riplLshiN+EXsPcUqWzH/iCWq4XinNsg5u6aTaQWtOiN6eJHgwYNKlZmqUrsO5fEv1afYOX+i1gscqpsnZBzrez3C9aQEFRo1AsGvANP7ARb99L75qXApmfEGB4bZ3BpBI+UCN7+oaCxARTRKFDY0qea5fibcqoRQT45y8CMbw6x8UQsP+yP4c2fT97+IKlKKIrC1KlTady4MQAuLi5oNBo0Gg2dOnXi+PHj5T9Z6PQy1okHPJqVfjLPyxBT4Zx9wavNjX17plxoPhRmJ8HsZGjzIOTniO6AoR9CnznQ9mEY8y1rztvxf3vEYV5tB1Tsy0tV4vSVNOasOs7WU/Es+v0cy3dH3f4gqebrM6fs9wN6lK73igZ6vyzSYns0u3H/nGvQ4znRNffiJWjYRVwTTAaY8Ct0exo6TIRRS8Q4HVsX8dNmbNV8rzqmRgT5mGvZRU1X+SYLpy5fvyaxVN2WL19OUFBQqfdOnDhB9+7dWbhwYfme6u1cYeJ2bvgz82gl5ryC6Gdr1L1425D5IoiXXO86dEapwzm8CN53h/fc4cBC6Pc6OSO+YcYXu3jwfzkYzTBi6CCefe298n5dqQqFX0mn8OE9z2ghLDrFugWSKkdQXxiyoPR7igb8Ohd3p+kdoHH/4u3jfoaA69JoD/y/4teqCr8+Df/xFPX78j4xle6B5dDpcXgmHMathplnxUOBdFs1Ind9cx9ntBoFjQI2Og29W8plQa2tX79+REcXz2vOycnhpZdeYtGiRcyaNYslS5YQFBTEAw88wBNPPHHz/kWPFgWLxZRIoPHXT9B5iuhvc/aH/m8Wb7N1godWwehl8Ncq0V8X2Kt4u9kEm54rXg3r9zmcsuvDI5OmEB4ejo2NDf/5z3947rnnan+fZx0R2qQBmoLWVlu9lgFtfG57jFRLeAaLZvaSq8Ud+Bh6vgTJkeKpvNfLxfu7BsC0fWIwbeQvIlVtycx1SWfgxHJRvy1G2DANXi6RM9+tsfiRyq3GjK6PS8tl0/FYPJxtGdmpYdF8UqlmWbNmDVOnTiUtrbi15YEHHmDJkiVl939bzPBZa7FaXOHa0CAG2r2aUdy3Xl5mE/yfI5jzUVX48qiWF7fpMBgMBAcHs3jZf3HwaUoLH2fcHOt33oWaNLo+IjaDPWcTaeHrTL/WMsjXGVmJ8GlLsVJcyfE3zg3hpTtYsS4pAhZ3Ln4ocPaHl4r73q+k5JCQnkvbhm43Xxa7nqh1o+v93OyZ0r8Zo0MDZICvwf72t78RGRnJL7/8wpQpU3BycmLt2rX07t0bk8l04wEaLUw/KNJTlpwnr2hv7HsvD60ORiwi2aDngR8VnvnVjMFgYOrUqaza+Cdv/5HOqyuPM/aT3VxOzr79+aRq0crfhWkDmssAX9c4eYsBs12fKT3OpqI374W8Wom01IpWNPWPWV606c/weB79fC+v/HCMCV/sJdtQxvVGukGNCfJS7eHl5cXKlSv55ptvyMoSC49ERERw6dJN0hLbu4tMWX/7r1glTu8IY74VS0negR0ZTejwX2/WR6i4urqyatUqlixZwsZTKeTkm8kymMg2mPjteOztTyZJ0t1p0BTuWyjquNYGHL3hb/+78/MN/RBey4ZXM0XinQLf7IzCYLKQYzCTlp3PwfM3Gd0vlVIj+uSl2kVV1VLL03p6enLt2jXOnDmDq6srHh4eZR/Y/pEKr/9sNpuJixPz600mE1999RXvvfceqqrSs2dPvv/++6IBgt6udtjoNOSbLNhoNXi7VO1SsyazBYsqxpFIUr034G3xUxl0N65/4e1iR1RiJmYLWFTwdK6iNTIKGE0WFIVqzVdSFWp36SWrUBSFLVu2cOTIEdauXUubNm0AGDlyJJ6enkyePJnMzMzSByX+Bb+/Dse+LXf+6cOHD9OqVSsaNWpEo0aNaNKkCe+++y6KovDGG2+wa9euUjMAHusdRL9W3ng62TI0xI/7O1fdimd7I5MY9H+/M2Dedr7cLtPnSvVbWHQKX26PZG9kUpV9xpz729Ih0B0vZ1um9m9GSKD77Q+6Q9/tiab/v7cz4N+/s+Vk7W4RrDED76Ta68KFC8yYMYPw8HBiY4srhLOzM48++igL334JmyWdxLx2vT10exYG33x6m8Vi4YMPPuC1117DZDJhb29fNKjPx8eHBQsW0K9fvyr/Xrcy9P0/SM8RI/xtdBpWzuyNv7vDbY6qXjVp4J1Udx29mMIL/w3DYLJgp9fwrwfaM7Bt7Z3elpFrZMT8PzGaRWy00WnY+fq9NW62Tq0beCfVXs2aNWPbtm1cvXqV8PBwQkPFQkOZmZksWrSI77/+iKIc1sYcOLsBAIPBwJw5c+jcuTOhoaHMnTuXy5cvM2zYMGbPno3JZOK5554jJSWFK1eucOXKFcLCwqwe4IFS6bgVxPReSaqPDl9IxmASrXN5Rgu7IhKtXKK7c/2Db22v2zLIS5WqdevWHD58mOzsbCZPngzA3K9/ISGzYCSszh6aDiIyMpJevXrx7rvvcuzYMY4ePcqbb75JYGAg27Ztw9PTk19++YWFCxdiZ1e1fet3Ys7ottjoNGg1Cg92a0TDBjXrKV6SqktIoBt2ehFK7PQauja9yZicWsLVwYap/Zqh0yjotQqzR7WucU/xFVGtzfWHo5J5/5e/0Go0vDGmHe0aud3xuWqTfJOFtYcvk5aTz+jQAHzrybraZ86coU+fPiQnJ9OmRRNOvd8fxTOYbyM9ePb5WWRnZ9OkSRM+/PBDjEYjL774IlevXmXQoEGsWLECf/+avRRnvsmC0WzB0bZmjl+t7ub6dUcu883OKLxcbJn3UId6s358ek4+qw9dRqtReKhbII52NfPvoSrtPJPAzohEQoMacF9H/1odFAvl5ptQFAU7fc2cj1/e+l1tQd5gNDP0/T/IM4pmHSc7Hdv+ObBO/DHczqsrj7P3XBImswVnez1rZvWtsYGhMkTGZbB0xwVcHfSMaeNI25ZNAZg1axYXL15k3TqxAMWECRP48ssvcXFxASAtLY3jx4/Tt29fNBrZyHS3qjPIRydmMXnxfgwFI5LbBbjx9bTutz+wlrNYVB75bA+xqbkoCjT1dmL5jF63P7AW2xeZxOpDl2jm7cT0gS3k7BIrKW/9rrZIk5tvxlRi9akcgwmzRUWnrftB/nBUMvkFfVYms0rMtWzaNHS9zVG1U1aekaeWHSLbYEanUbiQ6MKwYcPYvHkzH3/8MQCOjo58/vnnTJo0qdRNnpubG/3796+UclxJyeH0lTRa+7vS2NOxUs4p3VxylqEoiZWqQlJGnpVLVD0yco3EpeUWXdsi4zLFFM46GvjOxWfy6o/HMRSsQZBtMPGPUW2rvRwRsRlcvJZF1yYeeFTxVLrartqCvJujDf1b+bD3XBKqCvd1rPr10k9cSmXx7+dwsdfz0n2t8ariedM3ExLoxuGoZExmFVDxd627f5RxaXlFA1VMFpULCVn8+tNPHDx4kG+//RZnZ2dmzZpFy5Ytq6wM5+IzmL7kEBoFLKrKp493pX096RqylpBAd/zd7YlNzcVsUXmiXxmrjVWyLSdj+enQJZp7O/P8sGDsbaq/dczZXo+Hky1JmXmAQqMGDnU2wAOcT8hEU3BjbjBZOH0lvdrL8PvpOOauO41WUdBqFP73TO8qz4lRm1VrrXjnoRBOX0lHq1Fo7e9SpZ+VnpPPrP+GkZtvRqtAbGouK56yTjPav8d14Ls9Fzl98gSbFr1Ouy8yWbZsGYMHD7ZKeapSY09HXB30mCwqGkWhbysvnJycGDRoEIMGDaqWMmw9FU+esTiP9q9Hr8ogX8VsdBq++XtPTl1Ow8PJhiAvpyr9vDNX03l3w1/kGS1ExmZgtqi8NqZdlX5mWbQaha+ndee7vdFoNRom3tOk2stQnUKDGqBRxIA0rUbD8A7VP27mp0OXMRR0+9rqNeyLTGJMl0bVXo7aolqDvKIo1XaxTcwwFL02q3A5OadaPrcsdnot2Sd/ZdHs2eTni0VahgwZwiuvvML999/PrFmzSqWEDQ0NZdGiRUVrutcmNjoN3z7Zky0n43C21zOkvV+1l6GxpyN2eg15RjFvt4m3bK6vDjY6DaFNylikqApcLLk8tVklMj6jWj63LF4udrwwvPXtd6wDvF3tWDGjJ7siEgn0dLTKiqFNvZ0Iv5pOvsmCAjTykPX7Vurs6K8gT0e8XWxJTBfBfmhI9QWbiIgIXnvtNRISEgCIj4/nwoULADz55JN4eHjw/vvvM3/+fObPn3/D8Zs3b6ZVq1Z06tSJpk2b8v7779OwYdVlb6tsrg42jOthvRuU+zr4E5uaw+6zSXRr6sFD3WvfzZJ0a92aeqDTKAVTtxQekE9y1aZhAwfG9wqy2uc/O6QlRpOFs3EZjA4NqLYby9qqTme8yzaY2HkmAWd7Pfe09Kr0kfyF/cyFT+cA2dnZbNiwgdzc3FL7NmjQgKVLlzJmzBgA9u3bx4QJE4iJiWHWrFm8+OKL2NrakpaWxiuvvMKGDRuKjnVzc2PkyJH4+vry0ksv4etbe7NJSdWnrme8S8rI48D5azTycKRj46pLcSpJNVGNm0JX15w+fZqOHTtiNpvL3P7II48wffp0bGzESmvt2rXDza10V0VOTg7x8fE0bdq01PuqqnLy5EkSEhL48MMP2bp1a9G25s2bEx4ejl6vR5Jupa4HeUmqz2rcFLq6Zv/+/ZjNZnx9fZk3b16pbU2aNGHgwIG3PYeDg8MNAR7E2IUOHToAcO+997Jp0yauXLnCjBkzOH/+PH/88QdDhw6tnC8iSZIk1VkyyN+hqKgoQKy8NnXq1Cr7HI1Gw4gRIwDYsmULa9euZcyYMSxcuJDp06fXi2RCkiRJ0p2puxM6q9DSpUt57z2xilrz5s1vf0D8Sdj0POxfCGbjHX/uihUrmDx5Mnl5eTz55JM8/PDDWMq5bKskSVXkwjb4bSac+qH2r2Yi1TmyT/42Tl5KZfOJOJr7ODGmSyM0GgU7OzsMBgNPP/00CxYswNb2Fslt0q/A560hP0ssztJkINi5gV8n6DELNBXPi/z999/z6KOPArB9+/ZKm39uNFlYvjuKqMQsRncJoHszz0o5r2Qdsk/+9v4MT+DQhWv0aO5Jv9Y+FT9BzG74bphYXVFnD+0eAbMBWo6E9uMrv8B3ISPXyNd/nCcj18ikPk1o5uNs7SJJd0H2yVeCqMQsnltxhDyjhZyLR3lh//8wZaVgMBjQ6bR88vFHaPU2tz5J/DFQChpMTLlwbiOgQsRayE2Fge9AynmwdQGn8l1kJkyYwI8//sj69ev5+9//zvbt22nS5O6TcHy69Szrw65gMFnYey6Jb6b3kBcCqc76MzyBt9ecJM9oYdOJWN55qAN9fHLFUsgeLaF5Oca9xOwGU0EKX1MunFgBqhki1omg33IkpJwDZ3+ws24q61e+P8pfV9Mxm1X2Riax/sV+9XIxnfpGNtffwl9X0gAw5Wby1w9vc+ncX8TGxWGjhS9GaNH+Ov32J/HrDGpBk7pGX/zkbsyB6D9g1YPwZQf4OAiOryh32ebOnYuvry9RUVFMmTKFJUuWMHXqVC5fvlzBb1nseExq0brQGkUhMj7zjs8lSTXd4QvJRQtm5RktHIm4JOri1n+Ienngk9ufpHFf0BWkVFW0IsBDcf1e3Am+6goLAuDy/ir6JuVzNi4Tk1lFRaR7jk3Lve0xUu0nb+NuwdF4jagtS0i/GonFaECr0xHxnA1e+hxc7fIhfDU8sPzWJ3FpCFP3wbFvwMYJ9n8EFjPoHaBRTziySDwBAGx9CTpOKvs8+TkQtR2cfCGgGyEhIWzcuJHOnTuzY8cOduzYAcDPP//MQw89hL29WOazc+fOTJo0qVyrut3bzpdLyTkYzWYUkHOPpTqtRwtPfjtxFUNBZsTudlEiSJvzwAwc/xZ6PHfrkzS+B8ZvgIj1oLeHg5+K+qxzEHU8NRqM2WLf7XPgiT/LPk9WIlzaA15twKtVZX7NIr1aerIvMgmzRcXRVkcjD4cq+RypZpFBvgyqqrJ8+XJmzpxJdnZ20ftvv/5PmusXQj6g0YFXidWXTv8Ivz4pmubHfAvBoyDhtOivy0mCHi+Ipvk2Y+HMGnGsXygc/qL4HDY3yfdtzIPFnSEzVlyE+r8FvV+hY8eO9O3bl127dqHX67G1tSU9PZ0lS5aUOnzVqlUsX74cb2/vW37vifc0oZGHI5euZdOvtXe9WQ9cqp/6tvLm3w914Eh0Ct2aetDL+SocKWh109lBw27FO++YC3vfBwcvGL8efDvAuU2wejxYTDByEXR4DJoOhphdYuyNIQMOfSaOV7Q3b65PvwJfhoi6bTHBuJ+hxbBK/75zHwzht+OxZOUZGd7Bv8auky5VLjnwrgyvvfYa//d//wfA/fffz8CBA2nXrp0Y4Hb1COx4Cxw8YPB8cPIGYy685y4G3IDoi5uTCQubQnpBTnpFA1P3Q0C30h+2bwH8+S9xAXh47Y3bAS7ugu9HQn5B87mTL7wcB4DBYGDdunX07t2bhg0bsmHDBmJiYgBISUnh008/JSUlBR8fH06cOIGPzx0MLpJqJTnw7g5EbBCB2ScEBs4DvR0knIKvuxe3uHm3g6dOwjs2IiiDCOL/TAXbEmNYLBb4ZTqc+h4aNIdHN4JrGel3D30OW18u7ttvNgQmbqna7ynVenLg3R0ymUxFAf6DDz7gxRdfLD0XvWEXePTX0geZjcX97iAuBse+hfQS/eOqBeKP3xjEe70ofkBcYBZ1Fk38g+fDrncgORJCJpa+mLgXJ9CxtbXl4YcfLvp99OjRpU4/bdo0QkJCSEhIYPPmzTz++OMV+u9hDSazGOUfGZfJ/aEBVlkEQ6qnWt0vfkoyZJaeBXMtEs6sLa6TIJ7CDVmlg7xGA6OXih8QN/THvwX/LtDzJdj2sjh3qzGiXgNobcWgvzosM9fIV3+cIyU7n0l9mhLsV7UrktZ3MsiXcOnSpaKpaa6ursyYMaN8yWbsXKDH87Dvg+L3fpkmBtpZCufFa6DJADizDra8AHbuotmv8M4+9SKsfkTcIMQfKxiFrwHVBEnhMOAdOP4NODeEMcvK/Z0CAgK4//77Wb58Oenp1b/2851Y9Ps5fjp0CYPRwoEL11g8pRut/K07MlmqxwK6i8B8cYf43ZIPP44FFKCgJVTRidkxu98TT+bebUSzu21BF9y5zaLFzpgNiacLRuFbxPHxx6HXy3B6pfice9+r/u9YjV5ddZwTl1IxmlX2n7vG2hf64upwm1lK0h2To+sL/Pzzz3To0IE9e/bg5+fH2rVrcXSswBKG976PqPRjk1KxAAAgAElEQVQlaLRiAI5GDwPmirv0VQ9A2kURyD8rMcAm/VLx3TyIC4Ba8um9CTx5DLzbiv67b/pC9rVyFc3DwwOA119/nT179pT/O1nJ8ZjUovWiFcSoYEmyGo0Whi0U3XBFVFAU0NiKOv7wz2Lw3e+vQuYVuLAVlnQv3j3lfIkbfrVgFL5a/HvIYzD9kOiS+yhQ9PWb8qmLIuIyMJrFd1cUuJJivWXA64N6H+RzcnJ48sknGTt2LGlpaYwaNYoTJ04wYMCA8p8k6g/472Bwu26uuikPzPkiYIctgv0fl95uzIGcZPG6YVfQlrHojM4OtDaw6TmYZwcHP4HcFLhyADY/X67ivfLKK3Tv3p3MzEwmTbrJ6P0aZGiIH3Z6LVqNgoIil5KUrOvYMtg4E/TX3fSrFvFUr5pFP/6ON0tvTwovfh18v+ijv57eEVwCxMDa99zg7K+ifkesh7DFlf9daoC+wd7Y6bXotQr2eh1NvW8y4FiqFPW+uf7dd9/lq6++QqPR8PHHHzNz5sziJvpL+8QI2oBuYrR8WSI2wI8Piv45jf66JnqKn8Yz4+Do1zcev+c9QBEXgc7TYd98iu7wdXYw/FPR/3dhs3i/cKCkxQhpMeX6jr6+vmzbtg0XFxeio6MZNWoUvr6+zJkzp1KS6FS2h7o3xtfNnotJ2dwT7EVAAznVR6oCZ9ZBbBgEjxRN8mXZOQ92vi3qt9ZODKAtOf4GVQy4jf6jeI58EQW2vyr+7fg4NOoFl3YVb3byh2ELYNvs4kG1hXXflAsZVyvne9Ywr41pR2jTBqTnGBka4oe9Tb0PQ1WqXo+uT0hIoE2bNqSkpDBv3jxee+214o1XDsK3A0Rl0zsUTJGZWLzdZBCV8+CnwM3yx2sKLgqFA3RK9OFdT2cP438Rc+UTToh9FY2Ye2vrCpllVPhGveGxzcX9frfxzDPP8MUXxVP2GjZsyPnz57GzsyvX8VLtIkfX38LRpaJ1rDAd7ZQ94N+5eHtOMqx9As79Sqk6e0OQ13Dz+l+CrYsYXb/yQchJEMcpgK2buGHPL6NLquszMOyjslv4pHqvvPW73jbXb9myhZCQEFJSUvDw8GDatGmld4j6XTS1g7gQnF4l5sLHHhXvrRgMBxdSqoIrGjG3VmsrXts3gM5/L05re7MAD+Jm4ruhYrpO4b6qWeS8z04o+5irB8U0vbRL5frOn332GXv27GHlypXi8KtXiY+PL9exklSnnFkj6jWIeha+WtTx5POiteyzVnDuF0oHeK2YPldYvz1bixY+pRxPooZMWNYPchIL3rCIm4W8FDEFtyxHvxbN+Pmyz1q6c3UmyKdkGVh96BJ/hMdzq9aJ/Px8Xn75ZYYNG0ZiYiIDBgwoe/54o56gK1h4Ru8AF3fC+qlivux8f7i0+8aTtxsPY38Ur1UL5KXB2XXX3fnfgmqmzKcCiwkoI3GFxST678rZd6coCr179+bhhx+mcePG5SuTJNUAl65ls+pADGHRKZVzwiaDRL0GEbD3fwTrp8FnreF9D8i5blCrohGj3u/9j/hdtYhsdpcPlGipu5XrB9uVoNGAUsbTujlfDNI9t7ECX0ySSqsTnSHZBhMTv9xHVp4JRVE4EZrKC8Nb37BfRkYGAwcOJCwsDK1Wy9y5c5k9ezZabRkBtMkAGLtS3OFrbcQykoXpKbPjbtzfvTk8sEKkptToRD+daoKs2Lv/gjbO0OoBOFlGbnutXrQYFMpJFktfujctO7GOJNUyl65l8/ii/ZhVFY2i8M9RbRjWwf/uTtrzBRHkr+yH/Gw487NIZQuQl3rj/u0egd4vw8HPKArU5jzIybu7cqCILHruTcS143qqKlatLJQaLQbd+nUGz+C7/GypPqgTQf5sXAZ5RnPR4irbTsWXGeTXrFlDWFgYOp2OXbt20bNnz1ufOHiU+LlySGStuhlbV5j8h7gjN2QWNwNWBv+u4uYBFc6sLj63ohEXqaD+ou8OICcFPm8rbkZUi5j2EzrtZmcGkOvRV4MLCZlcScmhU1ADXOxl/2pFHTh/DbPFQn7BtKvfjl+9+yCvKNB1hvg5uhTOb7p5vW3QAkZ9JV7nXCvuxqsMbcbCiC8g+ncxXz4/S7yvsxODeDtPhaYFS0knnIIlPUXZVQtM3AqBvSuvLNIdOXEplaw8E12bemCjq3mN43UiyAc0cMBcEKv0WoUWvmUvj2owiLSzjz/++O0DfKkP6AbDP4Hf54gn5cJRtDoH8bTfqmDkfUqUmN96q773ioo7BisGwVOnwbejqOiqBbrNhMHXJc2I/kNcqAovFAc+vmmQd3NzIyYmhgkTJrB+/XqZ7raKbD8dxzvrTqNVFOxstPzwTG+Z+KOCWvg6o9EoYFax1Wlo27CSEyN1fAKSz4l1JIw5xfXb3gMe/xN824vfY3bDzncq97PP/iIG1Y7/peCJXRGff/9SaP9I6X1P/1hwI1JwfQlbIoO8lX2xLZIfD15CUSDI05Gvp3VHp61Zgb5mleYOebvY8fHEUHq28OS+jv7Me6jDLfcvz4psN+g8FV6Oh+ELIaCHyDyns4XwH0VaWxBT6YyVnLhFNYkn9KsHYPIOGPcTTNp2Y4AHaNCs+AKltRErWt3EwoULcXZ25uDBg7z++uuVW2apyP/2XsRgtJCTbyY338z+8+VLYCQV6xTUgH+Oaku3Zh6M79WYaQOaV+4HaDSiPr2SCL3/Ab6dwbHgpvfsOvGvqsJ391GukfQVYc4T62GYcuHpv+DB70VSnOsDPIBHi+JxBDp7kVVPsqrVhy6RZxR1+2JSNhevZd/+oGpWJ57kQSyL2rFx6C33KQzuP/30E3PmzCEoKKjiHxT2FST+VRxM/1ot5r92ngYJJyt+Pic/ccMQd4upS+Y8OLxYdAW0G3fz/fw6wYgvxSAiz1Yw8sub7tqvXz8WLvyEKVOe4OrVujkftyZo5OHAuYSCdbxVVa7sd4eGdfC/+yb62zHlifqdm1z83p73xYpyTv5gzKr4OT3biClyKeduvo8lH35/TVxDgkfefL8OEyH1gpjf33SQWNnyFowmC4pCjXuyrEu8XeyISc5GVcGiqjRwrHmtdHUmyJfH/fffz9tvv83Vq1fp0aMHFy5cqFjqWkOGyGJVMumFOV+sBZ2Xxg1pbW9LEf3mqgmi/4SjS7hpU3/keojaKgbatX7g5qfsOOnma9KXcOB8EnM+FzMBLl67g4uXVC6vjGhDvslCVGIWY7sF0iHQ3dpFkm4m8VTpRFYg+r+zk8QNgEZXelGa29E7wKB/i2P2LYCr+2++74nl8NeP8PcjN39CVxQY8Lb4uY0fD8TwyZazKArMHtWGkZ0Cyl9uqdw+eLQz/153mvRcIzMHt6TB/7N33uFRVGsD/83sbnoIgSSEUELvHaR3ld4sF6RYERFE5bNfK9der42roiCiCCKooAgISJHeWwKhBRIIaYQ0kmy2zHx/nCSbkLaBdM7vefYhuztz5t1lz7znvNXLtaJFysdNpeSz2636+fkRGxvLihUrnO/KlhYPuz8VZSgzUxFmO0X40To/AB5+4OkPV0uYd77iHnJMgKrJEVDX9RGxI9dyBfnYMkT+/rVKPuG0aHpRvxd4BxZ7yYSEBMaNu4PY0B0AWAM7cz7+Ko38ZXnJ0sbb3cS793SuaDEkxXH5pAiuteaKllcMUKOBaP2q2ynxIl6zwbK7yLlXqEaRU+9dDxr0ED723Ol3dgtcKkDJXzoAKReFRcG14Hij3KRn2vhs/UlsmtgwvPfHcYZ1CJI7+jKgfi0Pvnyocmcx3VRKHkSzlqlTp7JgwQIefvhhIiIiGDNmDKqqYjAYaNmyJUbjNV+LpsGC3o4ysu41RUpbyzHQaIDoBQ/Q+zlRBU+/ZjdQGNlRsjnXsYp0uRoNREer5xPgvVp5dxd12ucd49wWWDJS3JAUFR49JNJxCmHLli1MmTKF2KgoDK6eNB71JEGdBlKCwocSSfUi7TJ8010s3g0uULMJtBgBre6Ehr0d9TJajYPjv+C0Xz5PFL4u5rq7j7hftJ0AfZ6Hr7s6rAO6XSzUc7P3C9jwrJjfHv4w8yi4OGF9zDWf5dy+ual0S7vQi0k89PUups3fzemYsuk+NnfuXJ544glsNhuvvfYanTt3pmPHjrRr147OnTsTGhqa9wRzougSp1nFw5wEI+aKvtPZCj76kPC7NegpUuqKrYKlgGsBpltLKsQdhb+egqOLwb+1o2Ke0V3k6+Zm7+dZEfWpInXu+Ip8Q9psNq5evcrLL7/M4MGDiYqKol3nbnSd+SV12g9gVKd6NJZNIiTlwKbQGCZ/sYP/W3yAy6mZFS2OIO4YOSWn7ZliHo34HJoMcij40+vAxQuCujrS24rC5Em+26uuieqVMQfhp7FizuY0vVHE4t6ved5zdn7omN/p8QXn0l+Dh6uRR29tjlFVMBoUnh7RSu7ib2Iq1U7eatN44vsDpGWKle3ji/ax9rlBzvV0LwFubm58+umnDBkyhLfffpvUVLGYiIiIICQkhG7duvHxxx8zffp0cW03X9EpKjkSUKB2CzBl1XtPvgAxR2D5BLBl1cGu00m0m0y5ULgQfq1EJO+qqRS6MzjxC0xeK/rPZyTC4Dcdi4psajUXNx2bWZTbrNko5y273c4777zDW2+9hdkszJCKovDyyy/z2muvoaNisWl4ulWqn4GkmnLxSjr/+e0YmVaN8/FXeWX5kcph6gxoR56mUNl56SDM+JE7RBc6W4aY3/V6weVQSIsrcDgAWt8pdtz7vybHXH9tvM25zSJj5u9/i3GHfZx/HN8m4j6i2cRO36ehUx9pSt/G3NW9AQoidVNy81Kp7u7pFhuZNkdQW0qGFZtdx2QsXSWfzciRIxk5cmTO86tXr/LEE0+wcOFCZsyYwfr165k/fz61atWCqbtg13+F2az30+KEkJ9h5QOIHUCWac6WIdLdisyVz6p7HbIMbn9PVKyzZ8Kfs8ij8FvdATWC4F/LCh9q4Bxxs7mwE9pNQGt1Jx9/9BFfffUVsbGxOQsYk8lEkyZN+Oqrrxg4cGDO6aZKWLxBUj2JTc7AoIq5bNcqUR9xT394eDfs/0os5ntktXD++2Ux5zWbw2VmyxCd5PJ1nMuFwU3UqshIhGGfCGWfcjF/K9rmI6BuJ5iytvCx7voRVj4ESeeg34vCsucksrubBCqZkq/hbqJb49ociRRlJfu08C9XJeTl5cW3337LkCFDmD59Or/99htbtmyhc+fOtGvXjtdffx0fn1w76b9fFJM+N6oLoOeP0s2Nooh61HazuGE8uA12vE8eBd98FHSfWazMoafO8p8lV7lypT6s2kHk9NacPu1I1wkMDGTRokUMGTLEuS9BIikj2tarKVKMdAuarjOhVyXqn+DfWtTAyEazw4738kfTK0YnatXrcGq1uAdEbIXZ52F+z9yDQP9X8na9KwyvOjDlTyc/hESSn0ql5BVF4cNJndlzNgGDqtC9Se0KkeOee+6hR48eTJo0id27d7Np0yY2bdrEL7/8wqhRo6hfvz6zZ8/Gy9MfEsMBXZj52twNAe1h98diJW9JE+9hwFEYG+Gbs2dH8arCJ+jhJ4J+7BYRXd/mzmLlTE9PZ9CgQcTHx+d53c/Pj7lz59KrVy8CAwNxcal8uZvVCbums+7opZz+2LWLSKO5nJrJayuOEJWYwaTejRjfsxIpujLGzcXA94/2Zs/ZBPy8XWnfoGbxJ1UUipqVSZMsnhtcoMs0YT7P3pFnV5Y0uApLXDb2a2INkiOy+ktkmexN7iKeR1IlSM+08efhKBRFYVSnekW6P07HpPD6ryFkWO08NaIVvZv7l6OkBXNT95MvDpvNxp49e4iJieHtt9/m4MGDOe81bdqUhyfdgfuJH8GcTNfh99F3ZlbxmYwkiPhHRLl7+InymL9OhpO/C3N/vR5waa/YLRhcYGaISI35aZwI4Gs5GsYtAkPeNZiu6/z111+cPHkSgOPHj/P116Km9tq1azEajSiKQpcuXfD1lfnY5cUbvx1jY0g0dk3Hx8OF5U/0w8O14PXz7B/2sy88AbsGbiaVLx/sTuMALzYfj8WoKgxqU6fUgqRkP/kb5Pw/8Nu9YuE98ktoPU68nnwRog+Afzthijd5wsL+cDlM6PG6XUScjm4XlfNmhQm/+tKxkHoJej0FA1+t0I8mcQ5d17n/q12ci7+KArQM8uGbh3sUevzoD7cQnxVQ6mpU+fPZgVjtOv+ExeFfw5VezfxKLcbM2fldqXbylQ2j0UifPqI29OjRo1mxYgUxMTF8++23hIaG8u83PnQcvPorvjJ0Yvr06VkpdrlW6ismwZl1Ik+2TkfRzObMX5BwElqMhppZwTQPbi1UluTkZGbMmMHSpUvzvTd9+nSGDRtWKp9ZUnI2H48l0yYWy0npFs7EptKhkKI3MUnmnD4LqqIQl2Lmgz9PEB6XioLCuqPRfDTZCTOupOxp1B/+LyL/6z71xQNESeuvu8GVs8IN1/F+GDlXFLbJuCLaT5vcREnaWcfLV37JDZOSYeVMXCrZfbyOXUjCbLXjZip4N5+Ynrd5UXSSmSd/2E96pg1QmNy7EdMGl3JZ5mKQSt5JXFxcmDRpEgAzZ87kf//7H5GRkQDs3r2bvXv38uabb/LII4/kXanZbRDyEzmBeNEHRWGd5sPEwwl2797NxIkTOX/+PJ6enowfPx5vb1EUo3Xr1kybNu2GP99Vs5UMix3/Gm43PNbNhqo6/r/tGkRdyShUyT/Qvwnv/BGKUVXw9XShaYAXZ2JSsWRp/p2n4rHZNZnyVFWICxUuu+w21CFLYPSX0H5ixcp1DYlpFlQF2RyphHi5mfKUMgG4kppJUC2PAo+/p0cwK/ZFoigKHRrUJCHVTKbVjtkqBll9KEoq+aqAm5sbTz/9dM7zyMhImjRpwsWLFxk3bhwLFizAz89PvKkaRPRudrqNwSV/Glxu7DbRDevySeztp/D+ki288sor2O12unTpwtKlS2nRogXpmTZWHxI15zNtOh43kCWzKTSGOb8eAx0Gta3DnDvbl3raYnWmkZ8nIReF79bVpOLhWvh/xrCOQbSu50NMcgYdG/hiUBVcXVQsGRqqImphSwVfhfAOEm43AFTwaVT08eYU2PVfzOYMTD1nYfBtUOBh8Slm1h2NxtfTheEdg3KyEq6Hbzaf4ftt4QA8emtzJvcpvFiWJC8GVcHTzchVswi2dDGoReZNzRraklvbBZJhtdOxoS+xyRnYsyoPGg0KzQLLvx6J9MmXEr/88gtTp04lOTmZoKAgFi9ezKBBg8SbsSHw5wzh2xv+GdTP5dPJSBTm/Lij0PEBEeizfx5RyTbu/Q02nxeHPfXUU7zzzju4uLig6zoPfr2b8DgR+NPY34vvpve8bsU84v3NXEkTZiY3k4H503rQrE7x5TMlglPRKTz23T4yLHa6Nq7FR5O7lEhRn41NZe76U5iMCk8ObUW9QnYJJUX65MuJM+th4wsi/mbMN1AzVzBlwhlRujo9Hga9gb5/HnMu9meD3g93Mvn0ob60C84bnJVmtnH3Z9tIzbBiNCgMaV+XF8e2uy7R0jJtDH13U06JW4OqsPXl2+RCsgRsOR7Lq78cRdN0/tWjIU8Oa1Wi83efucz328KpW9Od2cNa4e1eTCElJ5E++XLmrrvuolu3bkyePJkdO3Zw66238u9//5s5c+ZgqtMOHtpW8Il/PQXnN4HdQuzfn/B/6zQOXbQRnggWOwR4wqLlaxg2fHjOKekWO6djUnNWiGdiU0nPtF93UZvcaYq6ruMic+dLRIu6NVj73CAyLPbrmsBN63jz8b1Fd1CUVGKaDRGPgvj5Log9Buiw+lGO2Jrzj94DDQNpePDOqhB+fGJQnlPOxKVisdmxaTo2TWdrWBwvjr0+0QyKQu61v0FVpJWuhAxsU4eNLW7FatfwLCSgtih6NvOjZzO/MpDMOaSSL0WCg4PZsmULb7zxBm+++SZvv/02b7/9NmPHFjFDI3dAugVNh22R6STl6o8xpCl8f5cLda4JqvNwMeDn7Up8ijjYz8u1SBNxcfznrg48t/QQaZk27u3bmIa1S9CZTwKIdp7e7nJxJLmGqzHkxOOoBnTfxnDF8bZeQHncBrU8curNmwwKbYKKcO8Vg5uLgRdGt+W91cdRFXh5XLsbMv3frLgY1Sq7+ZHm+jJi69atPPTQQ1gsFi5evOj0eQP79ebNQQqBSTtpUsuAMu5b0Uf6GmKTM5i/+SwADw9qSh2fG+9Truu6XOVXI6S5vhKw+zNhylcN4NcabfI6Xv1uHZvjfXE1Gfnk3m4FBmmGXUrhxx3n8PN25eFBza5rB5mb7Pu8nN/VB2fnt1TyZYjNZuPAgQNER0cDkJphJS7FTGBNNzxdc63g0+IgNYYajToz4PYRGAwGsKRnFeSQ0e6lzdnYVFLNNtrV96nWvkmp5MuXqCvpxKWYaV3PJ2+KVVwopF8WHeaMIro9LdOGq1Gt1r+/ikDXdUIvJmNQFVoF1ajWixrpk68EGI1GevQQQXanolN49Nu9KIqCegUWPdqLIN8iAqxcSif4SpKXH7aHM3/zWQyqQvNAb754sLs0X0pumE2hMfzn12MYVIXa3q58/2gvR+34gLb5jr/RnbmkYF5ZcZQdJ+PRgVGdg3hmZJuKFqnCkcvIcuLnPRGkW+ykZdpIz7Sx5vClihapQrDYNFbuv8BPu86TklFEff8yYtE/58i0aaRb7JyKTiU8rmzaGUtuLuZvOZvzu0pIzWTv2YSKFqlCSE63sHTneVYduIjVVkh3zTIiKc3ClhOxZFjtmK12ft13AZu9fGWojMjlZDnh7+2Gi1G0djUaVfy8C69vXp15bukhDkVcQddhxd4L/DSrT7maLGt5uXA1q5WxpuuyOIikVAio4UpE/FXsuvhdFdW/oLpitWk8OG83l1MzUVTYcTKO9yeVX/VGNxcDRlXBZhcuaA9Xo7TSIXfypY7VprF053nmrj+Zp5Xm/f2b0KeFP7W8XBjavi6jOterQCkrjr1nL5Np1bDYNC6nmolLMRd/Uiny3sTONA/0po6PGy+NbUeArPAnKQHJ6Ra+2XSa+ZvPkJyrhOlLY9vRtkFN/LxcmTqwGe0qc/OdMuJSUgaJaRYsdo1Mq8auM5fL9fpuJgPvT+xCPV93Gvp58MmUrtXaJ+8scidfyvzn12NsOxmHxa6x6sBFfpndnxruJtxMBt6Z0KmixatwmgR4cS4+DU3XcTUayn3H09jfix9m9C7Xa0qqB7qu88iCvURlLd7/Do1hyWN9UBQF/xpufD218MYlNwMBNVwxGhQUq8jHr4iCWt2b1uaX2f3L/bqVGankS5l94QlkZvmiNB3OxV+lYyF1zG9GPruvG/M2nSHDYmPqwGa4FtLoQSKpbKRl2rh4JT2nCFVkQjrpFrsMosvC3cXI11N78O3Ws3i5GZk+uHlFiyRBKvlSp3MjX3aevozVpqEg6ppLHNTycuXfY/JHG1dXLDYNTdOL7EEtqRp4uhqpW9OdmKQMdKCerzse8v81D40DvHjjXx0rWoxyI8Niw6iqeaqGVjakki9l/nNXB5buOk9CqoW7ujeQgV03MWuPXOLtVSFoOkwb2JQHBjStaJEkN4CiKHzzcA8Wbz+HosDkPo2lz/cmZu76kyzdFYFBVXjj7g4MaF2nokUqEKnkSxlXk4EH+sub+c2Oruu883so1qxI3wVbz3LHLXLRV9Xx9XTh8aEtK1oMSQVzKTGDn/dEYtd07JrOW6tCK62Sr7w2BolEIpFIJDeEVPLliM2u5QTtSKo3iqLw0ti2mAwKBlVh2qBmchdfzbHYNEpSJlxSdQnydWdir2AMqoKLUeXlcZU3zqhCzfV/h0Tz855ImgR48cTQlo4ykNWQBVvO8O3WcIyqwtsTOtGnhX/xJ0mqNEM7BHFr20Dsmn7TZRHous4P28+x7WQ8PZv58WD/JqjVtDCJXdN5ZfkRNp+IxcfdxNwHbqmQ9DFJ+TLjthY8OKApRlWp1D0IKkyysEspvL4yhCORSfx5KIoP/zxRUaKUOXHJZhZtO4dd08m0afzn12MVLZKknDAa1JtOwQOsOxrNt1vPcuxCEj9sD+e3/RcqWqQyY8/Zy+w6cxldh6R0Kx+sPl7RIknKCTeToVIreKhAJR9x+SpqVmSqxa5zKqb61hC3X2PC06TJXlLNOROTitkq6kWYrRqnq/P8vmY+S5ecpDJRYUq+W+PaGFUFN5OKm8nAuK71K0qUMqduTXfu7t4Ao6pgMqi8MFp2RpJUb25tF5gzt91MKkM71K1okcqMXs386NCgJkaDgperkadHtK5okSSSHCq0n3x8ipmdpy/ToLYHXRrVKrVxSxNd14lMSMfT1XjDTWWumq0YDWreXtMSSRlR0f3kz8Vd5UhkIm3r16R5YOX0UdvsGpEJ6fh5u1LD3XTd4+i6TkqGFU9XY6U330qqB1Win7x/DTfGVuIdvKbpPPfTIfaFJ6Dr8PyoNoy8gcYyXm7XfxORSKoajQO8aBzgVdFiFEp6po2HvtlNbLJokvTpvV3pcJ0lqBVFkdkTkkqJXHIWwdm4VPaHX8npmvb5+pMVLZJEIikltobFEZNkJsNiJ8Ni56u/T1e0SBJJqSOVfBF4uBjz5L16yEYUEkm1wdPVSHZSn6pwQ+Z6iaSyIpV8EdSr5cGjtzbHw8VAQA1X3h5/8zRekEiqO31b+DOkgwgQbBLgzVMyYE5SDanQwDuJRFJ2VHTgnUQiKTucnd9yJ1/KnIpOYc+Zy1iyespLJJLqga7rHI5I5ND5K7J8raTKIJ3MpciSnef5etNpVEWhXi0Pvp3Ws1L3GZZIJM4z59dj/BMWB0C/lv68frd030kqP1IDlSI/bD+H2aqRbrETdSWdsOiUihZJIpGUAhkWGxuOxeRE4v8dGkt6pq2ixZJIikUq+VIkoPiqRcwAACAASURBVIYbWZV6sWs6tb1k3mxJSEqz8E9YHJGX0ypaFIkkDy5GA24ujtulq+nm7ElwI1xKzOCfsDgup2ZWtCg3FdJcX4q8M6ETc349SkJqJo8MbkaQr0dFi1RliE8xM+WLnVg1DU3TeWdCJ3o1l536JJUDg6rw6b3dePf3UHTghdFtMFTTrnplQcjFJGZ9tx+DqqDrOt9N70VDP8+KFuumQCr5UiTI152vp/aoaDGqJFvD4siw2nMCFpfujJBKXlKpaN+gJj8+1qeixaiS/Lr3AmarHQBFgfXHonl4ULMKlurmQJrrJZWCujXdc7oSmgwq9WtLK4hEUl2oX9sD16wgZFejSmBN9wqW6OZBKnlJpaB3cz/u79eYBrU8GNAqgFm3t6hokUqVDRs2MHHiRBo1aoSiKMyZMyffMRaLhWeffZZ+/frh7u6OokhzsKR6cG+fxgztUJf6tTy485aGjOgYVNEilTqrVq2iffv2uLm50aZNG5YtW5bvmOTkZB588EF8fX3x8fFh8uTJJCQklKlcUslLKgWKovDggKYsf7Ifb47vWO1KCK9bt46jR49y66234uFRsJUiPT2d+fPn4+HhQe/evctZQomk7DAZVV4c244VT/bjiaEtUatZPMP27du56667GDRoEGvXrmXkyJFMnDiR9evX5zlu/PjxbNmyhfnz5/Pdd9+xb98+xo0bV6ayyYp3Ekk5oGkaqirW1H5+fsyaNavA3byu6yiKwty5c3n88cdvqOiKrHgnkZQPQ4cOxWq1smnTppzXRowYQUpKCtu3bwdg165d9O7dm61bt9K/f38A9u7dS48ePdiwYQO33XZbia4pK95JJJWIbAVfHM6Y6H///Xe6du2Kp6cnvr6+9OjRg61bt96oiBKJ5DrIzMxk8+bNjB8/Ps/r99xzD7t27SI5ORmAtWvXUqdOnRwFD9C9e3caN27M2rVrc14r7fktlbxEUoU4e/Ysd999N4MHD+aPP/7gxx9/ZNSoUVy5cqWiRZNIbkrOnj2L1WqlVatWeV5v3bo1mqZx6tQpAMLCwvIdk31cWFhYzlilPb+rl+NTIqnmHDp0CG9vbz744IOc10aMGFGBEkkkNzeJiYkA1KxZM8/rvr6+ed5PTEzMd0z2ceHh4UDZzG+5k5dIqhDt27cnOTmZ+++/n/Xr15OWJqsDSiTVhbKY31LJSyRViJYtW7Jq1SrCw8MZMWIEfn5+TJo0ifj4+IoWTSK5KcnesWf73rPJ3sFnv+/r65vvmOzjso8pi/ktlbxEUsUYOXIk27ZtIyEhgQULFrBx40Yef/zxihZLIrkpadq0KSaTKcevnk1YWBiqqtKihaj50apVq3zHZB+X21df2vNbKnmJpIri4+PDpEmTuOOOOzh+/HhFiyOR3JS4uroyaNAgli9fnuf1ZcuW0atXL3x8fAAYPnw4MTExOSl1APv37yc8PJzhw4fnG7e05rcMvJNIyoDvv/+ehx56iLNnzxIcHExERAT79u0DRGW748ePs2LFCjw9PfNM8LVr15KWlsbhw4cBWLFiBQC33HILwcHBzJs3j127djFs2DCCgoI4ffo0y5cv57777iv/DymR3KRcO79feeUVBg4cyOzZsxk3bhxr1qxhzZo1rFu3LuecXr16MWTIEO677z4+/PBDVFXl+eefp2/fvjk58mUyv3Vdd/rRtWtXXSKRFM/ChQt1QD937lye59c+goOD85wXHBxc4HELFy7UdV3Xd+7cqY8YMUKvW7eu7urqqjdq1Eh/7rnndLPZnE8GYL8u57dEUupcO791Xdd/++03vW3btrqLi4vesmVLfenSpfnOS0xM1B944AHdx8dH9/b21idOnKjHx8fnvF8W81tWvJNIqimy4p1EUn1xdn6XSMkrihIPRNyIYBKJpNwI1nXd6X69cn5LJFUKp+Z3iZS8RCKRSCSSqkOJAu/8/Pz0Ro0alZEoEomkNDlw4MDlkuzk5fyWSKoOzs7vEin5Ro0aIX12EknVQFGUEpne5fyWSKoOzs5vmScvkUgkEkk1RSp5iUQikUiqKVLJSyQSiURSTZFKXiKRSCSSaopU8hKJRCKRVFOkkpdIJBKJpJoilbxEIpFIJNUUqeQlEolEIqmmSCUvkUgkEkk1RSp5SZmg6zono1M4HZNa0aJIJJJSxmbXOHYhiYtX0itaFEkxlKisrUTiLG+uDOHv0FhAZ0yX+jw1onVFiySRSEoBm13jkQV7OBefhqbpPDOyNaO71K9osSSFIHfyklInNcPKX0ejMVvtmK0aK/ZGYrVpFS2WRCIpBY5dSOJ8fBoZFjuZNo1vNp+paJEkRSCVvKTUcTUZMKhKznO3a55LJJKqS01PF+yaaFGuKFDLy7WCJZIUhVTyVZyYpAxmLtzLhM+383dIdEWLA4CLUeX9iZ0J9HEjyNedjyZ3QZVKXiIpMaEXk7jvy53c9+VOQi4mVbQ4ADT29+LxoS2p5eVC8zrevHF3h4oWSVIEiq7rTh/crVs3XbairFw8OG8XYdEp6Dq4GlWWzupLkK97RYslqQQoinJA1/Vuzh4v53flwq7pDH13E1czbQB4uhpZ/8JgaRWTAM7Pbxl4V8WJSTaTvU4zqAqXU81SyVcivt8WzsJ/wvFxN/HBpM40D6xR0SJJqggWm50Mqz3nudlqJ9Nqx8NV3rYrA3ZN582Vx9gUGksjf0/+O7krtb0rn+tCmuurOJN6N8LNpOLhYqBuTXdaBflUtEiVjnNxV7ln7naGv7+ZX/ZGlt9146+yYMtZMix2YpLNvLL8aLldW1L1cXcxMqh1HdxdDLi7GBjQOkAq+II4sx7+21A8zm4st8tuPh7LluNxZNo0zsRe5bO/TpbbtUuC/MVUce7t25hujWuRmGahS+NauBjluu1aXlp+hPPxaQB89tdJujetTYPanmV+3bRMG6qi5HkukZSE1+/uwMHzVwDo0qhWBUtTCbFbYdkdYM3K1/9pLLyQDIayV21XzVY0hBnVrukkZ1jL/JrXQ4VoBJtd42xsKsnploq4fLWjdT0ferfwx81kqGhRKiVJaY7fmaoq5TYZ2wT50KFhTdxMKi5GlceHtCyX61Y0ZoudM7GpZFjkouZGUVWFbk1q061JbRm8WhB2i3gU9rwMua1dIP7ebri7GPBwMfDI4Gblct2SUu47ebPFzkPf7CY6KQNdh4+ndKGzXKFWaXRd548//uDEiRPXdX7Dhg2ZMGECqqqi6zqrV6/Gx8eH/v37l4p8jwxuxsdrw1BVhZaBNWhdTi4NVVX4eEpXIhPS8HY3UfsmSDWKScrggXm7sNg0TEaVhY/0kjEikrLDxRO6TIMji8TzTg+Ci0e5XNrLzcTSx/pw4Uo6ATVc8XIzlct1S0q5K/ltJ+OITsogwyICSr7YeJpvHu5R3mJISsiZM2cICQnJ97rNZmPx4sWsWrXqhsb/+uuvmTZtGsuXL2flypUAPPzww4wYMQJFyb+D6dGjB3Xr1nVq7HHdGnBLk9okZ1hpWbdGuUYnq6pCI3+vcrteRbNibyQpGVY0HVSrneV7InhyWKuKFktSnRn5P7hlhvg7oF25XtpkVGkSULnnd7kreU9XI1luDFQFarjLsIDSxq7p/Lo3koiENEZ1rud0MF58ipktJ2Kp4+NOv5b+KIqCpml8+OGHvPTSS9hshZtfvby8mDJlCjW8vcGcCAZXscouhoyMDJYuXcqWLVvYsmVLnvfmz5/P/PnzCzzP29ubdevW0alTJzRNw8ur6IlWr5YH9YqVRnKjeLmZMBpULDYNo6rgXUl3N1WazFTY9V/ITIEeT0LNhs6dFxcK4X9DUFdo2Of6rm23QsIp8K4H7jWvb4zSRlGgTvuKlqLSUu4atldzP4Z3CmLN4Sjq+Xrw3Kg25S1Ctefz9SdZuf8CZqvG6kOXWPJYb4J8izZhJadbmPLlTjIsdlRFYVLvYO7v05DRo0ezYcMGAPp1CKaWFg9uNSCwCxjEDbxWrVq89NJLNG3cGJaOgfObQddg9DfQcUqx8r744ou8/vrrXLp0CV9fX1566SUSExP55JNPSEtLy3f8li1bSE5Opk+fPtSuXRu73c68efO48847MRgMBe78S8pVs5WfdkWQadWY0CsYv0qYGlMZuadnMIfOX+FwRCIdg32Z2Du4okWqfiwZBRf3gGaDo4thdgSY3Io+J+YoLOgtzlENcNcSaDXW8b7NAqsfhfNboPkIGP6pOC43manw9S2QGiWe37cR6ldRK2xSBOydC641oddspzYkVZVyV/KKovDcqDbXrdw1TWfF3kiOXUhiaIe69G0Z4NR5CVczef3XY0QlZjClTyPGdWtwXdevCuw+cxmzVdSKNyhw4lJKsUo+5GIyNruGJavG/Loj0XhG781R8Kvn/YeR8e+LKFaDDTrUhbHX7LIvHRQ3iexI11UPgSXVYUorhMDAQL744ot8r//444/5D9Z1NnzxFENmfQJAQkICABMmTACgbt26fPXVV4wZM6bIaxbHE9/v53RMKnZd569jl/h1dn+MBpm5UBxuLgY+vc/p+jv5MFvtfPdPOLFJGUzoFey0FepsbCpvrgzBbLXz1IjW3NKk9nXLUOm5uNsRXGZNh+QI8CsmqPP0n2Azg24HO3B4UV4lv+sjCPkJbBlweCEEdoSu0/KOcfwXSLkI1qyF9+LhcNeP0Hx4qX00bJmw40NIPAu3zIR61/9bKhRLulisZCSAaoKIrXDf+tK/TiWhytnKl+w8z/wtZzBbNf45Gcen93ajU7Bvsee98VsI+89dwa7pfLIujDb1fGhRt3oWJund3J/opAwyrRqaTpGBZosWLeKDDz4g9WoacSlZhXUUCDMZ+C1OrNinTZvGyK51YW2Wn8VuEZPwWly9xQ4+G80K65+FGvWh5ejCBb50EEKWgl9r6PQAqEUo031fclviPJ7rDd8fhacfn45r3bbMmTOHK1euEB0dzdixYwkKCiIwMJC33nqLYcOGFT5eAWiazomolGyvEsnpVhKuZlLHRwaQlTVv/HaMbSfjsdg0tpyI4+cn+uJfo5hdKjD7hwPEp2YC8OySg/z57CDhGqyONOgDF3aKXbmLF/g4YS0J7ARGV7EoMHnk34EnnhMKHsCaAYnn84/hes390pwIP98Njx6G2s0Lv/bpdRC+ERoPghYji5Zz9QzHYiP0Z5h1AnxKeUOWGJ614NHAngmR20t3/EpGlduaHDh3JWeXqmk6x6OSnTrvUmJ6TlMFVVGITTGXmYwVzWO3t+DJoS25p1cw86Z2LzS6OSQkhAceeIDQ0FAiI85jTowhMymGzMQYkrMUfMuWLXnhhReg5Vhw9RIT3eQBfZ7LP2Dt5jDodVBy3VxtZojLH7An3rPAiZXwbV/Y+SGsfRy2zCn6w4VvRLFl8N7tEP2MgWeGB/P444+TkJCA3W7no48+wsXFhUuXLnHw4EGGDx/OM888g8XifFqNqiq0rueDyaBgUBV8PG6OyPjKwNHIpBxrkqoqnIvP764piCu50iQ1HVIqac5yqTDpDxjwKvR+FqbtK95UD2K3PfxzaHIb9H0Bej+T9/1uj4LJU8xvFy/odF/+MVqNg7bjgVzuMNUofPQFkZkKuz+FZXcKS8Hy8RD2e9Fynt/iWGyoBogtgwJSvk3A6A6KQcQONexb+teoRFS5pe6gtnU4FHGFTKuGQVXo1ti59Lt7+zbmozUnUBWFmh4u1bqwhEFVuPOWooNxbDYbc+bMAaBJkyasX78+ny9bURQaNmyIwZDlm5sVBhd2Qe0WULuQnNA+z4B/azGhdR0UFVoUsIu3pAmTWdI5sRAAscs4tRoGv1644K3vgLN/ZbkNXKDx4Jy3VFXlqaeeYurUqcTFxbF48WJef/11PvroI1RV5f333y/yO8nNZ/d1zeOTL4mp/s9DUfx5OIq29XyYfmtzaeYvAf1a+rPmyCWsNg1VgZZ1vZ06745uDfjzUBQo0LaeD4E+Tii+qoqLJ/R/seTndXlIPAoiqIuY37FHoG5X8A7Mf4yqwrhvhZLc/q7YCRvcoH6v/McmnodvbhHBgbldC6fXQKsiXGktR8PB+WDNuifU7Vqij+gULh7wyF7hk3erCT1nO3+uZodtb8O5TdDmbuFSKIUYoLKkyin5MV3qU9PDhVPRKfRp4e+0yX10l/q0rudDbLKZzsG+N2V5SLvdzsqVK7l48SJLly5lz549KIrCW2+9RdOmTYsfwN0XWowo/rgWI+H+zRB9UJjoCvIXnl4DKRccCh6EhaDpkKLH7ngvuPpA1B4RIFRA4I+Pjw8+Pj5cuXIl57W9e/eSmJiIr2/xrh0QUeIPDyp5cYsD567wwZ/HMVs1Qi8mo6oKM25rUeJxblaeHtmG1vV8iE/JZFjHuvh4uDh33ohW3N4+ELPVTtdGtUol+PKmw6e+eBRH/5cgqBskRwq/vkcBG6YDX0PGlbzuO5MHNL296LGH/hfqdICk89Dh3oIXG6VBzWAY8kHJz9vzmVjgWNMhai941YU2d5a+fKVIldR0/VsF0L+VcwF3uWlWx5tmdZzbGVQXNE1j7969xMbG8sknn+RJUwsKCmLx4sUMGjSo5APrOmQkCtOesYAbcf3u4lEY7rXI6ayjqCIlp89zxQbpAWInUNRuIAu73dHcY+vWrXTq1ImjR48SHh7O5cuXCQgIoGPHjsVfrwScjU0lyytEpk3jeFRKqY5f3TGoCqO7OKForkFRFDo2dG4BJ3ECTRNK2t03f5S9okDzYuJcPPyEpc1mFsFtdToIN0Gbu4o+TzVAl6k3JntZcmm/I7DYmiHcCVLJSyoKXde54447+P13hx/Mz8+PcePGERgYyJNPPomfn1/JB9bsIlUufCMY3eDeDUUr9IJoPFiYug58DbWawj2rnNtFlIDPPvuMdu3aERISwpdffklkZCQ1a+bN7X3ggQd4/vnn8ff3p3btG4/I7tncjy//Po2rUUVRYFTnoHzH2Owa8amZ+Hu7SlO+pPKRkSjS7RLDwbMOPLwLapSwykT3x0RA27m/hc/7X8vLrRJdmdLxPghbmeWKVPJmKGRhtthJSrcQUMOtUpQilv3kqzG7d++mVy/hLxs8eDBNmjThzTffpE6dOjc28Om1wuduuSqeB90ifFzOcjUWdv5X+Ph6PwMeuZSrzSJyf20ZwlznVjoZELNnz+bTTz8FwMXFhW7durFv3z6sVkeA1vTp0/n4449xdxeBileuZvLhmhNcTslk6sCm9GhW8IJo79kEXvvlKDa7xjMjW9Omng97zybQtI53vsyP+BQzD329mxSzlRpuJr59pKdT0ePXg+wnL7kutr0LW14TvnTFIILyRs51/vy447D/S/CuL3LQjbmCVtOvwLEfRYBf+8nl0kimSDnX/R+gwdCPoU4h1fL2fQkbnhcyj18hrA1R+6DRAAhom+fQ41HJPL5oH1a7TrM63nz54C24llFPEdlP/iZk+/btTJ06lYiICAAyM0VK0dChQ1m3bl3pXUi55kerluBnpGkwv5fwx6PAyd/hsVDH+z+NE3mruiYCY2aG5DcXXgdz5swhMTGRqKgo5s6dS6tWrQgNDWXWrFmcPn2aqKgo5s2bx7x58zCZTMyaNYu0Nv8iJCoVu6bz/E+H+PnxfgRcE9Cl6zov/HSI9KwyzW+tDGXt84O4q3vBgY8/744kIS0TTYMEeybLdkcw6yZpXCOpIqgGciLoFaVk8y8tHhb0EgF3RncRyHf3EvGezQJfd4Or0cJFd2o1jF9e6uI7habBdwMh/bJ4/t1AeDY2/2dNvgh/PSXcDpZUWP4veOoC1LulwGE//+skaZniXnAu/ir/hMVxe3vnym+XFdJWWI249957OXXqFJmZmTkKvk2bNnz00Uele6Emt0HzkWKiuteGUV86f645UVTM0mwij/5ymPBtgTCBZUfO28yiKlVKlFj9ZyTdkMg1a9Zk0aJFbNy4kVatRC31tm3bsnnzZi5evMjmzZtzjrVarXz88ccc3L3NkXapKlxKysg3rq4L33vOc/ScFDAQK/u9ZxOw2cVrriYVQ1ZQmEFRZOdASeWj26MQ0B5QwLcp9HvJ+XPjci3YbRkiCj2bK2cgPV7M7exMGl2H1BhRoKY8sWWImAN08chMdlgmc2O5Ku5z2WSmOv7W7HBuM0TuyIkvcnMx5Am2L6tdfEmQO/lqRGxsbM6/NWoIM7erq2vpRxqrKvzrJ7AtEsE1JRnfzVcU70g6Dygi8t6UlcevKODXCi6fFDt5kzsc+AZ2ZqW+3f4B9HyidD9LFosWLcrzvG/fvtw1dggrj1xGAXzcTbQqIJNDVRWmDWrGt1vPogAjOgXh6ykCEb/edJolO8+jKgpN6ngx76EeTOzViF1nLnM8KpkWdWswsVejMvk8Esl14+oN0/eJ6nPGEtaHCGiHsAIoIl4nd7aMTwOHFVA1gn9bUUzn1J9iBz3hN2hWTHZNaeHiCU1uh8ht4nn9XuBWQNEwv5Yii+fUn4AOt78nXtd1WDoOIraIvztMgdFf8fSI1jyxaD8xyRn0beFP3xb+5fN5ikD65KsRHh4eZGRkkJaWhodHJQhySbkEaXFi4uf2vaVdFqkoikEobfdcfuvUaNj4b7HS7/0sfNtH7PhBROm+lF4mfrx+/fqxfft23njjDe6++25atGiBoijsPZvAlTQLfVv44+1eeLOVmKQMbJpO/VqO733wWxtzzPhuJgPzp/XIye7Qdb3M07ykT15Splw5K/z2fq3yLvQvn4KD34hKl91m5M2+iTkKW18X+emt74DlExxlcn2bwZOny09+uxXCVgG6KPRjKGR+67oo+OPiDTWyAmlTY+CTRqJiHojd/iuWHHN/ZZrfcicvKRuO/wK/3it+/AHt4MF/HJPd06/wgjfedeGO78TfmVfz3jxUQ+kWntDssOZxYTa8LPL1BwwYkGPOBwoNtruWwJr5qwr6ebtyISFdGAR1PWeHD8g8bknVZvMc2PG+mI/t7oGxCxzv+bUoPAc9sANMWCH+jrpmQVlQKu6NYE4W96CYw6Jc9qD/5L1/GEzQ9u7ix1GU/LU+XGsIa0S2knevncesX5nmt/TJS5wj8bxoU5nbJ1UUG18Qfi9rGsSHQsQ/Jb+mqxeMmCtcAkY3GPddqQTh5XBwARxZJIIAM0Sjm7Vr13LgwIE8bXWtVitnzxZQqx84d+5cTvzDtXw4qQtt6vnQoLYHb/yroyyNK6m8xIbA+a1id1scmgbb3sqa3+kiG+ZqXMmvGdRV5MQrBqEkx31X8jGK4q+nRYxPygXRmvf0mtIb28UDJq0W/TYCO8O9f1XayndSyUsKxmqG5AtiQp9ZD1+0FTWo57aC9ITiz3evRU6Erq5lPb8Ouk6DlzKEmb7dhOsboyBOrRGpMVmFLVrXFoFx77zzDt26daNXr16cPn2apKQkunfvTrNmzbj33nuJiIggISGBixcvMmPGDJo0aUKnTp04fPhwvks09PNkwSM9Wf5Ev+sq3iSRlBmZqcI1BrDrY5jfQ7Sw/bYf2G1Fn6soonpdznPVEVdTEhRFtLR9JROeiy80Yr3E6LqI5Tm9xlFSV9dEEG9p0nggzDoOjx6Eup1Ld+xSRJrrJfmJOQILB4LdDP5tRCpMdpUnzSb8WIXVwM7mjh9EOlzqJejzrKiNfb0U1ZXueji3WaTCZH8mgxsfjVRx7zyWvaHnCAsLY//+/XTu3Jm+ffvmKPDFixezePHifMOFhYXRo0cP5s6dy7Rp0/K9L5FUKk6shF8mCmXY+k44u94xF+JDhXm7qBaviiKKV/06Wez8R30pgvWul9K0zoFYtGx+xfGZTB7Cn95qXOlep4ogd/LViNxlXJ1G08SOds0TDh/ZxhcgM0mkulw+KV5Ts4NSFPDOX8UtH34txCr330mi1nVJOfEbLLoV1s52pNiVFpHbHQ0wAOrdgvczp/h0/hJ27drF+fPnmTBhAmlpafz111+AKCbUv39/atWqlfPo3r07O3bs4NFHH8VisTBr1iyuXi0gDecadF0nITUzT6qdRFImWNJg61vw1zMiJRVgzWNibtszRZ0Kt5rkWN00O3g6YXVqPBCejoLn4oovVXstui4U8XeDYccHjvLWpUXuRYtqEkW1ZoWBVzlZ0zS7sJIUZxEpJ+ROvhpgt9t5//33sVgsGAwGR9c4Z/j7Rdj7uZgUh76FkV9m5YsqkN1RvfODokZ9XIj4u9nQsvgYDqIPwa9ThEwXdgrf3+h5BR8bFwobXxR++yEfgG+j4sdvNAhM7zp6a3edlqdsp4+PD0uWLGHZsmU5r3Xp0oUPPsgKJrJbRWlLzQ5BAfR+uCvfLXTBnGnBbDbj5eVV6KWtNo0nvt9PyMVkXIwq/3ugG62CCkjdkUhKg5/uEPEwmlXEn4z+Ou/7ugYjPodNr4jCMIPfhJpFd7C8YY7+CJtezmryskek1XZ9uOBjz26EHe9BzcZifheU5nYtLcdkLeTTRHBd10fAvWbx52VjThbWSg8/0VPj0j5o2Ed01yyOq3Ewv6co+OMZAA/vFsHEFYhU8lUUTdP49ttv2b59O4cPH+bIkSOAqOzm6lqCAK8zax2rXlsG/DFNmM9cvMQkaToEOt5fvk0j4kLJMTLZzPmjcLOxWWBhf1FrW1Egej/MPlf8+MF9YdKfwmfXoJdI5bkGVVV57733eP7552nYsCHTp093vLl0DERsA3SRS2xwwdNgwZxvlPxsOxVHWHQKVruG1a7x8dow5k3N30lPIikVIrc7IsDTE+CXyUKxGz1As0Cvp0Wv+ebDy0+m6IO5mryki+cFkXgOfhrraCudFgsTVxU//i0zRKnsSweEib4krkKrGeZ1hasxoNvFbjw76v+BrUW7MUCkBqdcEG7N1Esi4O96ut2VIlLJV1HeffddXnrJYQYPCAhg0aJFDBtWTHeoa2k2XOS12s1i8tszwY4Ipnkxbi2rYQAAIABJREFUHUylFBEecxROrhLpdK3GFR2J2niQWGgY3UTkbecHCz4uI0GYI9GFyS8pQvgb1z4ubgp3/AANexdyjYHiUQTPPfccEyZMwN/f31F3wJohzIG5W2jaMnKMHsVhMuROswEXo/SYScqQhn3h/JasWhO6+K0C1GgA/xdRehHh4X+Lym+NB4tFdFG0uRv2zwM0cZ9pO77g4xJOOUpm2y0iVmDHhyJ1z6eBqCPv2zj/eYoignSvJ1A39qio7ZGduw9gzTK7H19evJI3uuZKpVPAUPEZNfIOU0XZtk1UagoKCuKHH34gJCSk5AoehHnOVEDhHNVYeHGIkhIfJrpabX5NmOH3FtPsokY9mHEUhnwE96yEHrMKPs6zjlg0mDzA5CnK7f4yEVIuig5aS0bdsL8vODg4b2Ehoxt4+JNT1SsbJ++VvZv706uZHwrg5+XKMyPb3JB8EkmR3Lk474I0G0UtPQV/8g9h3doyB34YIlLxiqJhb3h4Jwz5EB7cVvhiu14PMd+M7mJ+Nx0iGuekxwuF/+u9pSN/bnwaih08ZH1HWSrS5JFV6rcYejwBAR0ARTSv6f106ctYQuROvorSvXt31q1bx6VLl0hJScHf/zrLJ0ZuE40XrkUxwIlfRVBOg16iDGRhZCQKxVq7ZcEFLbIbzqAL01voz9Dj8aLlqtkQus8Uf9tt8Pe/xY6k6VCx8g9oK3b7D/4DoctE7eukc3lrZWemOFpClhaKAg9uhXWzhU8+uL9weRgPAmauXLlSZPteg6rw9oRO2DUdQyVoQymp5oQsLVjJp0ZBxHah0Br2LTrCPTUazEn5K9tlE7Yyr8vv9FrRoa0oAjuKB4i+FGufEDv3DlOEMvdrIfzoM46KIFxdE/cqLeuz6Jow35c23oEi/33za2ITUTNYxAW1HAMdJhd/vpuPKAms2Us/a+A6kUq+nNl+Mo5TMan0aeFPy7o12Hs2gS82nsLH3cQLY9pSt4DKaQUxYsQIXn9dVI1bvXo1M2fOvD6BNLswbWvXFMHQ7fDbveI9Dz949HDBaTIXdonVO4io+2n78reHrdvVcXMweYjAt6K4chbOrBO79EYDYOcHsPd/4gZyaT/s/BDq94D7/hZFKdpPhs+aiWAXdLH6NrqJVfW16XepMbDqQVE7v++/odN9zn5TDvxawpS1jucDXqbZNz1J2LOHnj178s8//9CuXSFtK7OQCr76Ydd01h65REJqJkM71CWwpjsr919gxd5ImgZ489yoNni6lfMtV7OLCHPNkvd1XRPzVjWIuu2FFXM5/D2sni7mVPAAoQCvnVMN+0HIT45A1ga9ipYpah9E7RUL5DrtYdVDcPpPYZKP2iNM3F2niYBArzrQYhT8r42jgYxqEpbGQW/kHzv2GPzxiIjlGf4ZBPdz/rvKpvEg8bgRKomCB6nky5U/Dl7kozUnyLRpfL8tnP9O7spzSw9itmooCjy75CCLZ/Zxaqz33xdNW1q1asU333xz/UI1HgxNb89qEmESP05rusgrzUgQk0XXIXxjgQFqbHrFMflSouDEL/l96PW6wYRf4dBCCOoGvf6vcHmunIWvOonAFUUV0f6xxxy+RBBxA9EH4eJu4f9LjhQdpbQs35ligGl78/V6BsTC5fwWcezqR4U8AU6azFOj4e+XRLDdoDlQu3nOWzNmzGDPnj0kJiayePFi3n33XefGlFQb/rvmBH8ejsJq1/lx53lev6sDn6w7idlqJ+JyGgZV4dU7nTD5liZdHobD30HCSRFsZ0sHFPH7z55TkduFe6tW0/znb3hW3ANAROnHHBKV6nLT6X4xXvhGaDkaWo0tXJ6zG0T9DD3LH//AFpGbb8+1CLFnCp/94DfFzjhqL3myfbwC4aFtYpd9LT8MEUFzAIuHiyI7zhbqiTkqKvm51YJb3xTBe9UAqeTLkY2hMZitwtxk13S2n4rPqXGs63Ap0fl88Ox87A8++IB69eoVc3QRqCrc85swubt4iRWyrgkf25m/xI5et4tUkmwun4TNr4pdvskdFCPoWQrWrZBUlWZDnUu9O7te7D6ybyyHF0L/l0XQns3sMD3qmuNaNeoLn50tQ8hSt1PBCh7EIiJ7MaAaxQKhECW/b98+/u///o8uXbrw2GOP8dSdXQmJSsPNCLP7/c6M5Qk57om3334bEG6Up556qvjPKal2bA2LyzO/D5y/krM5ttp1wuOLr6FQ6rjVgBlHxPzOPTc/aSSiwLPJXZHy/FbY+RHUbCQW+2lZJWt1DVwLSGFTFJECV1gaXG6O/ugw7YMw9XebAZteyvu6anAErdXt7PCTG91FV7iCFLymOWQFMc8zEp1T8uZkWNhPuPhUE8QeEXED1QAZeFeOdGlUCzeT+MoNqkKfFn7U83XH3cWAu8nA2K71nRpn06ZNrF+/HgB392J+wPFhYtLaLEUf5+4rAu0URUywMQuEOc2nIQx+C+p3F8fZraL0ZehyOLZU7LIDOwgl234itBwr0st+vQ+2vetcLezcBLR3mA2N7hB0CzS5FabugkGviza1rjWE4q+TZRI3ucG03dB1OvR8EqasK3z83s84KmB5+BdoztM0jffff5/evXuzY8cOPv/8c8aMGcOa42lEJsOpBJi58ir7tm3IOSchQZT6/f333wkIkCVsb0ba16+Ji0H8djVNZ2j7urgaVTxcDLiZVO7pWYBiuhF0XZi+L+4pOsBUUcCjlljQZz8mrYbATqJf/Pjljk6QSRHw4wg49Qcc+FrMf59gMV8Gvwm1m0HIMvhlChz6ruSBrfVucQT6mjyEDL1mw+S1Ym56+Av34F1LxLwGEUF//9/Q+SEY8Kow4xeEqopGNC5e4hHc3/kc9aQIxwZCs4oo+2qCbDUL7Dodz6srjmLTdJ4Z0ZqRnW9gZ1wEmqazbHcEIReTGNohiP6tAjBb7ew8HU8NNxNdG9cqtHvRrl27+Omnn7hw4QIrV65E13UGDBjAhg0bMJkKiYLf/7UIEFONUKuZ6Ba1739Qq7mYRNdTASo1Gj5t4thpo4gWiwajMNcfXADb3hYmN2NWoZnhn+Qfx5ohzObJkSL9xr8N9Pu3MLXv+UxU4qrXAwa/4Vx3qquxwsIQ2LH4ghmXDopAwcaDRROca/jqq6+YMWNGntd8fX1JTEzM89qKxQu4a7Io7+vn50dCQgLx8fFFBt6VJ7LVrOCnXRF8ufEU7i4G3r2nM52CfYs/6TrIsNhYuDWcmOQM7unViDb1fEhMs7A/PIEGtT1Kv+jRH4+K5jAgFteuNYRvu9FAGPNNyXvBg7DeLR8vdrQgUu2eihR/x4WK2JjDC8X8N3mI4joFBaSlJ4iAtfgw4Wdvcht0my5265tehegDolJe91nOBcZeCRd55/VuKfpz6bq4r9gyxTWdbUttNcPcluI+ohpEr/k7vs8fX1SJkK1mnUTXdV78+QgZWX2/3/0jlAGtA/ByK6X0sVyoqsLE3o3yvOZmMjC4TWCR5+3evZu+ffuiZUWWqqrKq6++yssvv4zRWMR/4T9vOPxul0+KiFG7WUyW3x+GSb87L/yez4Xy9goCn0aQnJVj26C3mEip0fBFe5Ffmu1fs6XD+c35x7JlwjfdhR8w20SnqKIT1uVQSDgD6GKSOqPgLx2A7waKMQwuMP0Q+BRhFQnqUmSBjDZt2lCjRg1SUsSNzs3NjYkTJ/Lbb78SHS38fQ184NbQR2FTBAz+T/EySiqEuGQzX2w8hcWmkWnTeOnnI/z57MAyuZa7i5GZt7fI85qvpwu3ty+Dime2TDg432HGDl0GqgvYM0Q+d+0WMOBl58bSNFFbInQ51OmQlT7rKv5tP1Ecc3EvLBokLILZrjlrulCo1yr51Gj4soOoYZF9/wlbKRbW+78SkfqqEXrOdk7BH1sKq6aKc3wawiP7CjfBK8r1Bc2Z3OCRA3D0Bzj+q8gQ+CBApCA60462EnPTm+t1XZQazY3VXsq1lK+Ty5cv89dff/H888+jaRrBwcHMnTuX/fv3M2fOnKIVPIBXXUeep25zRMVqNqGknSU2RNSzvxoDsVlR9kP/K6JXJ60Wx5zbLMxcuQNoTJ7Q6s78413aL8xjuX1wugZhv4jCPLpN3Ly2zIFzW3Ido8PaJ+HdWrCgL6TFi9d3fiSC/zJTxA3k2I+O4zf8Gz5pAism53dZHP1R3DxO/Jbn5f79+xMZGcmyZcv43//+x9GjR7P+Pcbczz9jwVgDR6ZDTRcr7HhX+POyOH/+vPPfq6TMMVvteUoYZFqvo79DZUQ15U1rVVSxgAexy0467/xYocvg8CKRfx65DVqMhtvfgzsWwW1ZAaTHl4v5mq3gQezkW47JP17YyrwKHsR83vGBCObV7cLS9/O/ICnScYwlHZaMEfN7+QTHfN0yR4xlSRWWv/NbxOt2Kyy/R8zvjS/ldR3YbeK+8Ps0kQHkDJ5+0GwYxBwU2Qj2TPhzRvHnVXJueiWvqgozbmuOi0HFxagyrlsDfD2d2D2WEWazmfDwcBYtWkSLFi0YNmwY//wjerG/8847PPbYY3Tu7GRbw38tg7rdRGDa7R+KWsou3sLX3S+rWt6Z9bB4BKz7PzHJCiI9XpjRISs/NQ5ueVSUus02nfm3dvi0VBeo00nUmx/4av7xvOs5gt/ykWvBpdth0WD4rLnYHZz8Q7gDzIki4nbdbHFcjXqOIB2Di8hvBWF52PGuyJ8PWQI/51qRH10iUm0OfSsK9JzK22vax8eH8ePHM3PmTJo3F1H0fn5+PDbzMR7qZsI390ZCMdCpUydANLLZtctxU0nLtJFhqRyNKm5GGtT2YGCbOrgaxfx+YmjLihapdFBV4ceu3UK44sbMF+Z61xrCH939MXHcgW/gh6Gw/X1Hjvm1pMU55qPdIhbKPZ8U5vTsnXadDg5fusEVmo2ACb+JaPpr8QnOVfUtF/nS+GwiAPC7QcIyseMDEXhrThRz/UBWvwrvoFybFbtjfi8ZLRYoSedg+9sitTabDc8Jt8DB+fD9bZBwusivMweDS966AsVVrEu/Uny8UwVz05vrASb3aczQDkHY7BqBTuaplwXbt2/nzjvvJD4+Pue1Nm3aEBwczN13380999xTsgF9G8MjexzPuzwk/GQ+waLYxOWTsOyOLLPbZuFHu/P7/OMY3MSNQ7MCCgwqwDxdtzOM+06Y9QPaiXrNhRXQ8W0kjt38KqRcEibGQpW+LnYlW/6T1W86a7WuWYX/DGDAa+KzRO0RJXM7ZlXCOp1XcXNxt+Pv8I1562dH/AMtRhQiQy5UFcYtgpUPiBvOiLng6sWyZcu47bbbOHz4MHPnzqVXr14s2HKGhVvDRXrkyDaMcTKwUlJ6KIrCnDvbEz24OW4mlVpeFV9mtNRo2BseP+l43myYSHELaA81gkSJ53Wzxe87cruoHdHzifzjePg7cs8B+r6Q/5gOU4QlL2yVuE6/FwtvAd18uBjj8EIRp6PZ81oA8qCLBfvRxaLORbYl0G4RzV5AzLfl44X1sXeuttVRe/MOdWadaGsNEL4hK10QsUG5dCBPymuh1GoqZP/nTWGJvDN/a2lALJiWjxexQ0ZXmLzm+nLyywGp5LPw8y7fyZ+amsrUqVNzguiGDx9OSEhIjoJv1aoVM2fOZNasWYUG45UYF0+RE59NXKhjh24z5580IKJ3v79NmK5UEwx5X+TFFkTbf4lHbk6sFN2v6vUQEzC7SES78eJhtwpz+bons5R2Aa4SXReLgNZ3icmXniBW2wOyrASuXiK+QNeF3y8jUZje2k0Si5psWoxy/N0yaxeQXcCj6ZAiv7o8tBvv+JxZ/ze1a9fmmWeeYcqUKfw/e+cdHlW19eH3zEw6IYUkQGihhtCkhCpNRKWIglgARbAjiuVe6/1s91quvVy9olcRxAIKiIgCCkoJhi6911BCEkIKISSTmTnn+2NlMimTBuns93nmkcycshNnnbX32mv9ls1mI/1CDrPWHMGuy+/z1i97ub5bE0xKBKfK0TSN8KDqm7xXGfXCCpapJmx1tWl2dnwrzLYv4ZepuY2WPGDCEmjWp+hxmib263SiIPa28SNRmYy6yTW51jTJBxj0nKjZ7f5e7DsvWdcNukP26HfNBQx51jibYgU2l+oZXRdHn31OEuJaXys27KRzvtyAdje4cn4MHZq6+Z2KY/CLMPB5+T2Ke/Yej4HDv8piI8cmmhsP7S77PaoQ5eSrkLS0NJ588klSU1Np1KgR8+bNy/ts8eLFef/evXs3HTpUgaZ58ysLJtk4jTQ/h37NNU4dHA5Z8RanJV+Y47Hww+1iaId/k4nC4BcLHmP2EKfZuJsoXyXuzM3sNQBNJiH1wsSh+wTCQ3vkmMAWooblxDAk7L5rrhi1TwO4bwOYpsNfn4F/U9cWBYiwzy3fy+/T+lpoNaR8f7tCxn/kyBGee04Snfz8/IpMzEp6XigUlUK7URLCdkqsdp5Q9Jidc10RLcMsOTetypi4tvlTydVx2rd3EEReX/AYn0CIvl9UIpc+Csn7XF3xQJx5SJRECjx9pYvk2QPyXv7Mdls2zOgLCdsBQz6/J1Za0B5cIlG+/PkBQ16Wcr/kA9BlQtlaUOenuCiFE81cMAfAVHNdac0dWR1j3bp1jB8/nri4gglvzz33HPfffz+TJ0/mjz/+YOrUqRXv4K0ZMOdGmcm3HAK3zJNs0noNRa52348S2m93vcyW17wse9TtRkiduoe3GLJmkuz5/HrwCdslIhAxWEKETrJSZRXt3N+yXZCHQv9n3WfMN2grKlZnD8IX/WVfMKwz3LpAMuWdEQAPH1fNfn6S98Oe+a77ZZ2FJY+Iut6ZffL5J1eI43cK5bQbKa8KYPz48Rw7dozw8HCefPJJ6vt4MHVoOz5afgCTpvH86E4VF5FRKPKTelSaMaXFSe/0694R+2wSLY7w6Epo0kvC+zmZ8OvfxG57PSSKkcfXiH06xWPyc2y1hOnbjnDJWhuG9J4/tqrglte6d8We3H3PIwbBg9vgyB8itOXIkT3/YR+AX6jrHJ8gkawuzP6fcltQ5zrW5H1SalsvDFIPy+vAz/DwXrmGyVR898qKoPmVEs3bPlvyIEZdgupoJVNr6+QNw2D78TSsNgc9WgZjMdfcHMJjx47Rrl07bDYbJpOJ1q1bc/DgQVq0aMG6deto3LgxhmFw5syZyhFSWfEPWPeOGJbFWzJm+zzq/tgtn7n28Tx8Ydj7siLfMTu3D7UPXD9dQvb7F8P8cbndmsyirBXYAn57CtZ/IEqUuiNfVycLDH4JBv2f+3s7cdjFyfs2KPvyN/UYfNiuoAZ/yyGy3+gM6WkmGPzPspcWlQNnnfyBAwfyEvUA7A4dTdMwmzR03ajScH1trpO3O3S2HE3B29NMl2aBaoJUEl8OlZwaQ5d95AmLiy8j++k+2P61ZOJ7+MLE5dIc5vRWQJf37loj0rWrX4G1r4sN+oXBgzslMe3bUXDsD7F5R47Lvs3ecNuC0nNb7FZ5vviUQ69g/2KYOxYMp31rsmDYMw9ScpPqPP1lD729m4z/ysKe4xIR0/XSIwAVSJ2vk39v6T4W/3UKNIgKr89/J/es0gfB4r9O8s2fx2ga7Mv/je5UYkZ+YGAgISEhnD59Gn9/f9avX8++ffvo3Lkz/v4yO9Y0rfKU0rJSXMpzul32yYojcWfB2XnSLkksca6Q7VnyHkiSnfNYs7cYYtQYed+ZSWuygJGrO23YIeVA6eM1W2RPvTwERUgC3srn5V4eftLK8tAyUe+yXZAJSkj78l23nAQFFXxwWcwmsnMcPPz1FrbFpdKqYT0+mtSzWis4ajq6bjDty83sP30O3YDR0U15bFjl/n/Lj2EYTF9xkFV7E+naIognRnbA01JzFxFkp7rsU9MKlHQWIWG7q9QOTRykoZNX1aKZJOoV3kOEs/L6qmtS+mrLhBNrXQlyeXr4ckiZSvcsXuUX6mk7EqJulGgdmijZ9XkEkvfKPr1zshHcpnzXvVQsnpB+UqqAUg9LUuK4HyuuTXcFUIO/uSXzw+YTZNkcZOU42H0yndNpZdd9v1QOnD7H20v2ciw5k/WHknnlx50lHh8YGMi2bdvw8/MjPT2dTZs20a9fvzwHX+n0+7voVnv6y151SRrTnSe4+rN7+EKn8bJXn/+9jrfKsWGdJDIAEk5v0DY3kS9fdMiSm5nvVV/O71mObnnWDPhiIPzLQ6R0rW5a4uZn0P/Biw742yl4Kln2+fs9KfdsHC35AB3Glv3+btB1nb179+JwlL3eetFfJ9l9Kh0DiDuTyYxVhy9pDHWd+LQs9sSncyHHQbbNwYKNx0s/qQJZtuM032+I4/jZC/y64zSzY45U6f3LzdA3XPYZ3FYcTXH0fDD3WF9Zlbe6BqKnFHyvZW5+SnA7116z4ZAonclSMDc2oHmuTHSufbcfXfZxpx6D/7SDf3mKDHZxJX4gK+Rb58HzNvjbCXgsTrYbb/xCnkfhPUWhrqzNpiqS5U9Lkp+hyxbGzm+rfgwlUGtX8g3qeZGYLjNSTYMAn6pbGSWkZ2POjRrYdYOTZ4upL89HWFgYLVu2ZNeuXZU9vKI0aAuPH8/tNNVGElyKo1kfuH+zCEg06yv17yBd3U6uh2ZXQmjuqsrkKaE3NOgy0ZXZO/glWVGbPEQ+t3EPiN8EDa8oPgHm3CnZww/r7Lr++g8k41+3y39j35HubyAJgVu/gMbdoe/fXfKVmlYwNyD1MGz8WFYb547LA83LX/YVd30nTTo63iYZvIUwDAPdcLWF1XWdG264gV9++YUBAwawYsUKPD1L/97Z7DrObTGHYWC11xFBlkoiwMcjz5FoVH3ly+m0LHJyBbKsdp0TZbDvaqX1UHF65xMkUlWSlGu3u6BBpHSla32d2Er0/SIrnXJQJgj+jWSbzdNXbM9kEZ2NwBYic9v+RulT79NAtDgs3rJH3qxf8RG4M/sgaac8P5z2uXSaNIxClwqbDmPl2oYhtn3oV6mCyZ8QbLaILoaTY6tFEc9wQMy/Jctf0yRRb/uX8nzqOsm91LVhyOtSQ+z2rHyNs8h9JtYcau1K/v07etCxSQAtQ/14c3z3Ku3T3CMiGH8fj7zGExOubFni8YZhcN999+U5+EvqGlcedF2Sz95qKEIwgS1KdvBOQqOkpt7p4EGS1brf43LAKYdh4wfIt9qAPd+LVn76CRjwDPxfFjx7TowobrVksBfn4FMOS7/oRffA/3pIcg6Iip2zfl53uEKH8X/BdzdJac6KZ+C1erBngftrzx3jCidmJkm5EMjs+6d7pXXsJ11d6nm57D6ZxnVvrGTAv37j3SV7MQyDdevW8csvvwAQExPDr7/+WvrfEhjVvQkNA7zxspgI9PXkroGtynTe5Yq/jwdvju9Gy1A/OjQJ4N07epR+UgUytGMjvD3M+HmJfY/p2axK719mrOclofathmIHoVFl02pv3k+cff7JcIv+8p6zocv+xdJoCsQGt3wKf30hqnNjv4bnsuGxY9ImNnmfJO0W5+APrxC7XnQP/DdKdOghNzLnXL0brq2/HV9LnsCeebDwTni9gdS5u+OHCa6cgNNbRCwLJBFx2eOw4mn4vI88P/Kzcy686guv+sCWz0v/m5XEkJclUmrxljp7d1UM1UitXcm3DKvHjPvLUftYgfh5W/h26pVsPnqWRoE+RDYuuYnB6tWr+fxz+SJNnz6dTp06VcUwpbf71i/EOR5dKY5t1CcVc23dAfkFQ7NSJGFv+VMwdZdkxC+4A/b+IDPrP98SzWlTbunJ8bVSmhdxlThoZ3YvwKaPpaSt9zTJXrWek9V371whj9OFDN5hhQW3S8lQ4cx9W6FVmDPkv2eea9JgOEQPIF/C0MsLd3Fy318cW/pfjixqQ/+WM8jOLljne2HjTDj7HiTvw36h+DyHAF9Pvps2gOSMbIL9vPCoyfu7NYTebUKY83D/arl38xA/vpvWn10n02nbyJ+mwWWYGFcHa16R1a7DKivrZv1kcl4R6HYK2HfSTll5x7wm9eAmizjPlEOyj99hrMjgguT/HP1Dtuia9ZVaeqcdmjxh30LZQrzmDZh9jdhfg3auUH9cTEG7zU6B+ePhETf5PIW7XGanyuLm6B/khYPS4kQx09nPQneImJWzlG/JQ6LRn1+8K+WwNOM5vlaijBGDZGvA2RkvP2Ed4YnTsojwb1KlyXdlodY6+erGz9vCoKiGpR8IpKdLIszQoUOZMmVKZQ6rIOcTXTNYPQcyTpX/GoYhzRrS48QInTP9kHbQ9S5pR+lUs7JnicEf/V1m9k4NeYAze6TUp0Eb+OUhcd6aBk37Qvf7pFZft8ue4KFf4a1GItX52FGJDgQ0cyXrtBhEgQcQyINCtwGFnPyID2W1gyEPpuvekfeb9hHDd1jlvqEF9/Jy7A4OzX8NW2YqWUnHGNqnMznWgmG4Ca8u5J3GYNMhPQtMGsV2BDSbNBoGXAaCLHWE0PreXNXBzQO9JpFxyuWoHDmQmVj+azjsEhGzZ8m2lbMrY+QNknx3IlbsytDF8WYmiS1nJIjjd7LzW3HyukOaRSXukGdHr4dkC+Fwrt6GhjTK2jRdMvH/Hi/jDoxwlclGjZFGMfnFc3KKyccZ+BysytXe8A6Eng+Lkw1p70oq9Kwn1QFODMO1+nf+nH+ln50O/+spFT7OicK+hfKMKK4yx+Ilz6gaSM2actRxfH2reEXQ8RYRo3AmvbmTqyyNmNekkcSyx+C/HSEz2fVZr6lFV86GLkIVzixYJ7pdEmUMQyYGtkwJxx+PkTyAK5+S83QH2M6L4X8/Vn5u0KZgNm5IO7h3nTh7k4dMEPo94V5GN3IUPJEgPeafSZNwGsANMyQyEDUW7vi1yFbCkyOjsGVKzXBYRCQZ585htVoJDAzkg3ffJswPdAM2xcM2aUzH/w1rSEBABbcTVSiKo8/jrqRW70ARlCkv826VbatfHpKfoFQQAAAgAElEQVTOkE5nZ/EUmyqM7pB9+V1zCr7vlfu9P3sAEraJbdsyZRU/+CVRowtuI6tsW6bkynxzvUwqglu7HDyILO74n2V1b/aUMPh177of/+AX4JHDUgr4ZDJ45k6kJ/0BV0ySxOF7Ygs+p8wWuPYdubbZEwY9X1B4J3l/7iQgX4ahPVua49RC1Eq+kjEMgwULitkvrmzqNYRpB6QGNrhNwT04J6c2Sag9YjCgwfInpS6+ywQRktn8P9eetiNHZuxO/euY14qGw4PawJKHpSmO2Su3XEeTpDynmIZfmOhUg2Tj+wSLsfZ/Gl7N56gdObBwMtz2fdFxN+wMd62SVb5hFEycy0iQhLqGXWRyUFjuEyQ34do3i/3T2RL2yfA0jVMHd7Fz505sNhuRkZEEBARwtzGDPfsO5K0IQv29aHnvf4u9nkJR4YR3h0cOiVNq2EUm9PnRc7O9TRbRVc9KFWeedkTUHyNHiRa9c188ea+swBvnNsBa/mRB3QnnPb8ZCb7BMsHWbRK96/O4fJ5/xYwmzWU8vOHGzyWXZuYAsOVG/jJOQuy70O9vRX+31lfDw/tkO8A7UARznKQckS28hl1k1R7cSl758W8k9yyOPo/AFXcCRtF6/ZDI3Cqh3NJfk0UmGs6mP7UM5eQrmccff5yvvvoKgNGjy1FeUlF4+UPEQNfPDpskmx1fK8YTt1q+0A3aQZvhIoZjzxKDD2rtcsxO4ta4nLy3GzGL5D3i+M7slnBf8l7JmB+Tr/HNxF8lCceeJe1qnStwi5ck//yVzzj3F2wDW4TCIbLDK2DujfI7+TeWHtHOEGQZ+fXXXxkxQvbnx4wZg8ViKdL5r96Df9Jr3buiDd6snzxwGlRxja5CUa9hQXnnrDTRiU89IrZ+JldPPWqsJJceWS6OecF4Ubt0qlk6Ob7W5eS93ESlTm6Q8z18pbLFmZHf/yn53LcB3DoffntCzh8903Vuo65S4pe43fXelv+5d/Ig23mFm8qs/48k02lm2Scfv/ji98ALT4qceAdI/tCmjyUC2rSP/E2cW5W1DOXkK5mTJ0/m/bvKsupLIuZ1SSixF1qBn90voT9nD2hHjmTN9rhfZDANhyjW+TWUh4fZA676l+znXciXme7c67JdEIO+Z23RMTTsDPe7aYYDorC3c46E9DSTTDTckXNB9gaDWsqDxckfz7seWhmGSF12Ll/3voULF6LrOkOGDGHu3LnuD/IJkqxahaImsfBO2f92itU42fGVRNecK3OTRZLL2o0SG8YQQSuTxSVbPeZLmN6l4LWc5xuGlKb1dNNvve1weRXGZBJFus96Svjb7CWO3x1ZqTK+0KiC23ArX3Dt1R9bJc+oyqiND27tyt+p5ag9+Urmyy+/ZNCgQQB88kkFZbZfCglbizp4kL227ve6RDUsXpJo13Oq1MD7BIvhb58FH0WJEfoGw99PweB/QdTNMPKTXMGcXNGcbpPLPz5PP5i8CloNleSfib8VPSbzDHwUKSpT77csWF5TL8zVWc8wCk4Aysktt9xSbCKdQlEjSdpV1MGDRO2iH3TZp2c9iUCN/BhaXQ1egZJA++vfYfa18jwIiZR8ll7TZG/7mrddzwezp+jZl5eGneDmudC8v+QQ3OBG8z1hO7wXAV9eDf9pK9tv+X8PJ4buvv5dUQC1kq9k/Pz8ePzxx1m9enW5VNIqje73yEzfSYNIWfkOfR2iRouKXeJ2SWpzJqONmQnzxsmMX7dJO9eN/5VMU7MHDH7edb1WQ+D4nxAeLQZdHGlxsPZNCRcO+EdBZ9wkGu5cXvQc5+r9yHJx9M7M4jWvwrgf5N8jp0PGaJnhe/jIHuTwD9yvLBSKukb3eyVXBkP2kf0ayYT9hs9k+6xpH7HftiNcyWZ3LhfluZQ0SZA9GSsNqtqPkojViP+4rh8xUGyw5dWukjR3nNos4e6g1nDlEwUTZ9vfKK/CXEiRbYY/34Kcc/KeI1uiEM4Wt7f9APNugwtJIlP97SiJODTsfEl/trqMcvKXG+1GSgOK01sl2a7wPnLjrvIqjJe/hPJ0mzjX1f+EjHi4/uOCxzVo69pHs2XL6r+wTrU9R2psM5MAkwhv3LGsaPJMfjLPwCfdJOHGYXM1rjF5FEzKqR8uWwHvNpfku8wkmHuT1LEWtwenUNQVBv5DOs6dOyGh+MICNS0Huz/PM1/eiu2CVLaM+BCiHyh4XJOe8gLpaGf2KirAk3ZcyuhsuZ+fjJVqFv9GxY87YbtIWJNb3mbylLJfk0WiiE7Cu8MDm+HtxvIsyEyEr4fD308We+nLHRWuvxwJ7yH69eVJFBvyqqzyneh22DZTat/dEfsu/Lu+vP76ouBn5xOkFtXQc5vWHISPO7nUqtyx81tpb5mTIbN7vzBJ7GnWF67+d9Hjz+cL8TmsMiFRKC4HWg+VBNbyNHka86UIuTjRbdL/3V2XUsOQqpfXA+GNYJcynpPEHa6SOIdV+r3/pw3EucnPcbL2dVm952TIJD6gmZQGth8tpXD5yd9wC0TvohzdVC83lJNXlI16YTDlL/DN9+Bw5MCuuUUNzJohMpu6TY755cGCYhP+4aJ7nR97liTNucOeI/vszr12k4dUAjybBnetltyAwuS/vmaSxMIycOrUqbySR9XeVHHZ0LAzPLhDVt5ODAfs+6nosSc3iA6Gbhen/NN9BT8Pj3apVzqxZYpCnztyMqV5ljm3lt3sIVt4z6bD2G+KRgoCIyhQw66Zil9sKC4/J7//9Dn+7/ttvP3LHjKybKWfoCjI2G8l8QZkJb7mVdjwn5LPKYzZIpEErdDXL3/Y3UnCDni7kZTkeOZ2u2rWF65+reR7hHYgT4zH4i0PkcJYMyTKsHs+6DpZWVn06dOH5ORkwsLCGDVqVPl+L0W1E3vgDE/P2crnKw9hd5TQ1UxRFN9gEYlxTqZ1u2jDH11Vvuv4N5JGNPnRTDK5L8y+n+DNEGkm4x0sdtp+dG4NezFoWsEQvsks+TeFOXcKNn/q6oVxmXJZOfn0Czk8+MVGft+dyKItJ3nmu21Vct+//vqrSu5TJbS+BgY+73oQ2DJzdaLz4eUviXwmD5mdj5xeUNEKpHbeks8wfUPg5u+K3m/5U6JH7bBKTfrI/xa/es/PqE8hqJWsTK64UzKI8+OwiXTl0mmiY73obhYtWpRX8rhjxw7Cw908lBQ1ln3x5/jH99tYvS+Jr9YeZfqKg9U9pNpH74ekd7sTRw6c2lDwmKa9ocPNsl/u6e8+Qz68Z0H7DmkP175V9Lifp0hJnCNHwvV3r3W/ei/MrfPkmeHhKxOTwjXsGQnwcWdpUjNnFGz4qOTr1WEuq8S7U6munvM2h8H++HOVfs/p06fzr3/9C6CIoEqtpfVQSbyzZ8sMuv2Yosf0+5uU37lLvAPRpz7zjMhjNu0LIz5y3/zB7CWrAGcrR7Nn0WPc0aANPHqo+M/PHhDt79ya+p/mz2HSfJHqvPPOO2nYsPS+BIZh8NnKQyzeeoo2Yf788+Yu1PdRJXfVxYHTLnu22nW2H0+txtHUYjqMhaMrZFKdv7+8E02DMbNkwm3xLjqBB5GKvZAk2vcdb4VBL7iSZfOT354NQ0L1ZSFiEDx1pvjPj62U7UKn7sdfn0Pvh8t2bSd2q4h2HVsl1Tkjp5ety18No/aN+BJoFVoPXy8LNoeO2WRiQHs34eEKxDAMnn32WQAefvhhnnuumOYGtY3wHjB5pSTUhEeLPKY73DltJ5omJXjFNXxwMuxdSNwm8rUtr5Z+0RWBfxPywvmahfc3e5KTc55hw4Yxffr0Ml1i3aFkvo2NI9vmIC0zh/eX7uOFm1QpT3XRo2UwmqZhNml4mE1c27l2KpRVO13vlHB4/CbJfXFm0xfGXa8IJx7e7lf4hRkzW1baOZnSSyJ/e+tLISQq38LAW9T5ykvsO9LJ054NO76Ra7gT/6nhXFZO3tvTzJdT+vLrjtME+HowrEvlhWOzs7O59957SU9Px9PTk1deeQWLpQ79uZv2lldlE9waHo+Dswdh/jh4r7kY2sDn3K8MysKWzySMZzJD4x4Q3Bpbg2PARv7xj3+UuZFQ8jkrzgQgm8PgdFpWyScoKpUmwb7MvL8PMfvPEBHqx4DIsNJPUrgn8np5VTYRA6Vx1JE/JEF31xwJv3e8+eKuZxii0LlpulTfhHaUSco1xfepKJb04y51vVrcoKZO78kbhoFRKPO7QT0vJvSLYGTXJphNlZc9/dVXX/HNN9Jq9Ysvvrh8upM57JLw4rCXfixA8gHY9T2kl1Dn6rDBpz3g9F/S2Gbli9Kn/mLITIYl0ySXwHpOxDdu+a7s2wD5GNg+DD8vC35eFrw9TEweWEKdv6LC0fWiZVMRofWY2L+lcvCVhS0bzsWXvWTt1CZJbM1OL/6Yc6fg6+uklDb9uEzmk/Zc3PjiYmQS77CK3LbZU7YVSoo6FEfPqbld/gKknK/b3Rc3pmqmDi0tC/LNn5J442kx8dptXenTphw1oxXAmTOyXzRlyhRuv/32Kr13tXE+ET7rLQI0viFw34aSmzocWw3fjHAl8d2/WdrIurtugW53BiTulL3D8pK/RzXk7dk5oyyvvfYaCxYsKNNqPtDPk++nDWD3qXSaBvsQHlTFrYQvUwzD4OUfd7FsezwN6nnxn0nRtAwtXxMixUVweivMGiI21LgrTFpZ8pbcpulSFaOZRI526u6CLV2dJO2kQEmcoUvOzMVo0ueczxfhM4rvQ18WGnWRLp5Ju6DhFVJGXAupkyv55Awrn/5xCLtucCHHwQvzd1TZvZctW8YTTzzBf/4jZWXBwaVkgdclNvxHktnsWSI+s66YHtBONn0izjsnQ/67Z5774/wbF2xhqZkufm8+oKno4jsJbAm6g8ceewyQ/39Tp04t8+X8vC30at1AOfgqZOORs6zck4huiK2/8dPu6h7S5cFvT4A1TcSoEnfBvlI6RK57L9e+z8tKPm61++Mady8YSbN4SWvci6HVUPDN96wIaX9x13Hi31gqimqpg4c6upK3FaqPrap62a+//pqJEyfm/ezt7c2YMW4yz+sqzkx4kNW52U1WfX5Co6TMxp4lWbrFdZwzmWHqTgnTZyZKL+xGXco3NrsV/nhOmtnkF8Y5dwKOrWb3bpejiIoqX/KP3aFjGOBhqZNz5hpHjt1lzwaSSa+oAsze+SpdjNK3uEIiIe2YZLkbDplQu6NeQxHiWf0veW5c/Vr5G0tdOCvNdc6fhvQ41/v7fhRJbHcaHGXFbpVyQXdVBLWAOunkGwf6cEP3pizacgLQ+PuICsrYLAFd13nrLakD7dmzJ+PHj2fkyJG0a+cm/FxXyDgtr4adpfSlz2PS2jV+szSn6feEiF0cWwWtr4W2wwqe3/8ZOf94jNTddrqt+Hv5NoCRl1Dr+vs/JHxoz6JAAMswwOLF0qVLAXj22Wd5+umny3zZZdvjeXXRLnQDHr6mHeP7RVz8GBVlom+bEKLC67PrZDpmk8bjwy9xtaZwT8phWYmHdZIQ+PAPYPbV0uCmzXXSJXLL59IMqsvtrj70Tm6cCYvvk+tc+VTJDasatIWbvrr4sX43Vsr1dDcCZ6ZLcHMrnpWGORYvuHV+rWx0pRVOTCuJ6OhoY/PmzZU4nIol5bwVT4uJet6VW7tsGAZjxoxh0aJFAGzdupWuXYvpk1xbOLVJvuBe/jDsAwhsXvDz/T9LNyhTbs/3e9e79ud0Xd7f8wMsnCgPCosPjPsR2lxb9b8LwBcD4HiudrbZS1YhtgvQ434Y+V8GDBzI2rVrWbNmDQMGlC1UqOsGg19dkbeytJg1lj55Ff7F1Mqfy7LhZTHh5VE1KwJN07YYhhFd1uNrk30bhsGZDCv1vT3w9qydK6xqZe+PsO4daNAOhr0vdp6fmNdzV9YatLte2sM697qd9r3iH7DhA7EjDz94cLtUw1QHb4RA1ln5t8XHFW247j3oVfbttwKkHIGPO7ryeHxD4akkt4cahkHaBRv+3hYs5qqJ6JXVvuvkSt5JcL1SwsUVRGxsbJ6D//HHH2u/g7eehy+HigKVZpKZ+sN75bPtX4su/YVkV6vX1MPS/tVZL2/K/ZIfXOJKmLNnwZEV1efku98r2fmGLkp8D26HgBZ5Y83IuLgEncKTZHdTZsMweOXHXfy64zRmk8br47rSt23lajTUdTRNI6x+CUlfiuJJ2g0/3C62eWqT1KjfktuDYuULkp2emUTet3n/T5L1HthCfnba94FfXPatmeDUxupz8p0nwNYvAEP6Vjy8V9TwLqX/hKGTp6Uhb7g9zGpz8NCsTew/fQ5fTwuf3N2LlmE1JxFUbSJeIgcPHszbhx8+fDg33uimT3JtIzNRusOBK9M1K1VKXRbfJ8l1TgcP8nDwcZNg2PoaMTSQ/0YMvvSx2bJFL3/xFMmwLytdJ8HtS6QGd8o2CGoJJhN2u50XX3yR7du3AxAUFFTmS5pMGk9d3wGLWcNi0rh3cBu3incHEzL4fXcCdt3Aatf5908XWR6kUFQEZw+4KlocVohbI02gjvwuyXKZiRRxaJ5unFaba132begijHWpZJ6BX58QHYuM02U/b/gHEu6/7j2xb0+/S3PwIKqZPe6XRYHFG2743O1hv+9O4FBiBjaHwbksGx8tL1szrKqiTq/kq4JHHnmEo0ePEh4ezptvXoTgQk0kMAKC20itqmEHNPg0WurJtXyhUc0k9aO9pkHzK4tep9NtcsyR36HtCGg34tLH9uNdsP9HSYbZ+S08ckhKXM7shg63lNyzOmKQvHI5fvw4EyZM4M8//0TTNJ5//nk6dSph39ANo7o35ZrOjTEMAx9P9+ZUWI+hMvUZFIpSaT4gN2lOAwxJWpt7I3QuVOpr9hL7Hva++0S4oa9LNOzMHug6WfbVL5WZgyDlkIxr70J45KBEEjKTRYnPXSMaEIceVQlJzsPfhyEvy9/LnTw3Ys9annomWEw1a+2snPwlcvq0zDbnzp1bbgdRYzGZ4Z5YeKOBiNoYDtGh1kyiHhW/WVrHDnkZ+v295Gt1vEVejgrq+Be3yrVHpplk62DbLMCQ/tf3bYQmZVtR3Hbbbaxfv56GDRvy7bffMmTIkNJPcoN3KXvsrRv6Mzq6Gd+vj8Pbw8wLY+rI90RRO/ELgUl/wP96SKc5PQcO/Qo3fSNZ6BdMYvO3LiiaLJsfk9mlB18R9m3LlsoXpxzt+dPw9QjR0Qf49TH4ezz4lD3aViEUzlcoxNUdG7F0ezwbDp8l1N+LaddFVtHAyoZy8hWEv3/JX4Rah6cfNLpC9rH13NV8UEu4cwUcXi4Pg/AepV/HboVvRkqnusAI6SAX0Ozix9VmuPSwt+duF+z7EVdo0YBlj8E9a92eunLlSlatWgWAzWZj/fr1AKxZs6bSqyAeG9aeh69pJ7N+1adeUd2EtJdVelaqrIIDWkhnxwd3SX5NWCcJV5dGRgLMGixbAM36wcTfpCX0xeDhLaIzZ3bLFmBghMvBg0zu170ri4sahMVs4v2J0djsOhZzzbNv5eQVxTN+MSx/UkJlg18U1aqfH4RtM2UVfdPXpavO7fgGTq4DDEneWfGMtJK8WEZ9Knt/506KzOT3N0srWife7mf5s2fPZtKkSUXev+qqq2jbtgLCjGWgqrJuFYpSsXjCXTFSWmrxEm13ew58M1wS6Cw+MOl3CC+lscuqf0riLQac3gJbZ0DvaRc/rskrYeN/ZWHR62F4v4WI6TjxDrz4a1cyNVUnQzl5RfHUC4MxX7p+Tj4A22dL72eQXtClOXnd5tK5NvRLD+uZPQqWxNyxDD7pBpkJUK8RXP9xkVMMw8jLl4iOjub666XxRlhYGHfddVeNm3krFFVCWAcY/6Pr593zRbrWYZXXr3+Du1aVfA09xxVeN4xLt2/vABj4D9fPE5fD7KHSa6JRV4iufV3gqhvl5BVlx2ShQNZtWUQmutwBmz+BM3slPDjklYodk38jePK05Ai4UaTSdZ2xY8fmKdrNnDmz7uROKBQVidkjX8WYVramTQOfl1LZrFQIagXd76nYMTXrA/93vlj7VpSOcvKKshPcSpSrYl6TkpIxZVCo8vSDB/6SulufYHmQVAbFPABiY2P58UdZrcyfP185eIWiONpdL8qUexeKZvuID0s/JygCHj8hQjS+oa4a+opGOfiLRjl5RdmwZUnCW1AreCZdSlnKGubWNNGnrgaysqTL3KBBgxg79iK61ikUlwEp562s3JNISJePGTh2LpqlHJNxs6Xa7FtROsrJK0rHMGDWVbktITXZl5/0e3WPqlRSU1N5/vnnAfDzu4h+0grFZUBmtp2J02M5n23HpGnc1LNZjSsDU1w8ysmXk19++YWffvoJXdfRdT1PKc1UwwQQKpQLZyFhqyvh7tgqqWktqZd0NbBw4UKWLl2KYRg4HA6WLl1KQkIC/v7+PPnkk+W6VnKGlVd+3EViehZ3DWzFtV3CK2nUCkX1sjc+nWybI6+b37Id8XXeyR9MOMfri/dgd+j8fUQUXZpXce19FaKcfBmIiYlh/fr1bN68me+//77I53379qVjx47VMLIqwjsQvAJErx4N/JsUq/5UXXzzzTfccccdRd7v1asXc+bMoVWrVuW63gvzt7P9eCoOHV79aTftwwNoHqKiAYq6R7MGvji7cXuYNdo1ql+9A6pkDMNg2pebSbsglQCPfbWFZU8PwbOGlsBdKsrJFyI9PZ2YmBgcDgeGYbBkyRI+++yzvM89PT159NFH82qrAwICuPHGGzGbS0kM0XWIeVVEYdqOhE7joH6TS9dXrgrMFrg7RmrcNQtc+2aNG/fq1avz/j1y5EgAWrVqxdtvv42nZxmyhAtxKjUr78Fn1jQS0rMr1MnrusH8jcfZeSKNazo3ZmD7sAq7tqLquWC189HyAxxPzmRUtyb0ahNCkF/5v3fVQcMAH969ozuz1hyhcaA3D19Tt1fxDt0gPctV6mdz6JzPtlVoQ7Nsm4Mv1xwhPi2L2/q0oEOTgAq7dnlRTj4fx48fp1+/fpw6darA+xaLhQkTJtCkSRPGjx9P586d3V/g3CnYv1jUo7JTIDsdOo8XGcYN/4G1r0vXpmOrRISi7XDo/agoyQW1rPxf8FIIiYRxC4u+fzxWdK+t52DQiwVrXKuQHj165E3Gfvnll7z34+PjmTdvXrlr4Sf0jWD67wcwaRrB9Tzp0qxiRTjmrovjfysPkW1zELM/iffu6EG3CDdNfhQ1hsOJGWyNS6V1WD2OncnEw2Lius6N8bCYeGPxHlbuTSTHrrP5aAoWk8bkPo24t91ZCO0omhM1mO4RwXR38/1bsi2eN3/ejUnTeGFMZwZ3qP0JdhaziWGdG7Nqn7SNvaJ5UIVPyF79cRer9yWRY9dZszeJ7x7pX21dE5WTz8e3337LqVOn0DSNUaOkbaqfnx+PP/44PXv2LPnk80kwvYtkoTtypJGLyQyxb0vbw/jNrraMICIx+xfD4RWAATfPgfa5Hex0B6QeAb+G4F3DQ2fzx+WG8YE1r0hTmmpoN3nNNde4fX/ZsmVkZmZSr175Wj/e1rcFXZoHcibDSnTL4ArvWb752FmybQ4A7LrBnlPpysnXYPbFpzPli43ouoHNYWAxa5hNGit2neb9idHsO32OnNw9bZD/p7NiTzBhy134kg33/AkNZXFgtTlITM+mYYA3XqX0PahOsnLs/PunXdgcoo3xwoIdrGo/FFMdaLD0wk2dGXE0BbtDp1frkAoXxNp+PDXv+2AyaRxNOq+cfE0gMzMTgGeffZZXX321fCfHrRG1J7uUbGE4QAfSjsLcMZB2zM1JBthzHf+qf4qTt2XBjH657SBNogXdrO/F/kqVj7NZDEgI35ZVLcP48ENXTW/79u0BCAwM5LXXXiu3g3cS1SSAqHIcf8FqZ//pczQJ9i3VoId0aMRfR1Ow2nQsJo0eLd10+VLUGFbvTSLb5nLiNoc4+w2HzqD/9gwfZ87Di9NcxzwcuY9VDR2TNR00m0i1jvpEEjn/t54sqwMfLzMz7+9Dw4BiOqtVMw7dyBOrdP6sGwYmar+T1zSNnq3KZ3Mp560cS86kTUN/ty2l8zOwfRg/bz2Fza5j0iCycfUt1mqdk8+x67y4YAebj56le4tg/nVzlwqZDcfGxvLuu+8CF9lsJjRKHDuQ18LRyaGlBY81echqXTNJK1fNBOcT4eeHIXGbqMM5+7UvfxruXlP+8VQVwz+ARXfLvyNvhLDqSUA8f170rT/88EMefvjhKr9/WmYOd0yPJSvHjkOHd+/o7jb86eT6bk0I9PVgX/w5+rULpX14DY/YVBFnz1t5Zu424pIzub5bE6Zd265GyA63aeSPt4c5L/oCOiYMwknAFPsGDQA0eMF4i9e0p9DQeUr7GG8jR5QhT8TCzw/x/dFWpGd2xGFoWO0Ovl9/vMZmstfz9uD2KyP4NjYOMLjvqjaXbf+FgwkZPDBjA5qmYdLgyyl9CQ8qvhHP48OjaB8eQFJ6NsOuaExgNeZn1DonP29DHH8eOEOOXWfdoWTmrDvG5IEXHx52OBz8+9//5qWXXsLhcBAdHc0991yENGNYR7h5Lqx/HwIi4Mhv0kTFHXpu0odXgOg+W8/B+XjY/N9CB2ryma5XnpLUpdJ5PLQZJk0k6jet0oS87OxsXnvtNTZv3szSpTKRqq56+FV7E8nItmHNXe3NWn2kRCcP0D8yjP6RNXuvtqp5Z8le9pxKx6EbLNx0guhWwfRrG1rdw2JIh4aczbCyam8irRv6c2bLQrzsaTzEzALHXaet5lokCVSr1wSyfSW6lbQTknbiZ4zDRDsceGJGxy/jMFAznTzAg0PbcWvvFmgaFZqYVtv4fkMcF3JkgmfS4Jet8dw3pPgufWaTxvXdmlTV8Eqk1jn5lPM52HLTnm12nZTzOZd0vXfeeSdPMOXJJ5/klVdeKV82tmFIgmDbqskAACAASURBVJ1XfYgcJS+AJY/AxlJkIbNTwb8pWNOLuzgk7YGlj8DIj8o+pqrGJ6jqezwj/78++sj1d4mKimLMmDFVPg6QB6AzjGkxa4TWv3wfiJfC2QwrDl2iYAYGaZmXZt+XikM3uGC1U8/bwq19WnBrnxYShTv5E8RvcHtO3jQ34xT4hhXIxRnPD4xhKfXIZJXRjyv37oCt70K3uyr/l7lIGvir73KYvzeeFhM5dh0Ps6lW/U1q6PKweMb0bEY9Lwt+XhbqeVu4uVfzi75WZmZm3l7uE088wZtvvlk+B5+VBh93hrfC4D+t4Vy89Dn/pEfpDt5JRjGrfSeGDbZ+WfIxlyn5dejNZjNLliwhMLB6WlEOiAxlTM9mBPt50q1FEI/U0BBsTee+q9rg7WHG19NMg3pe1VpaGJecyfVvr2L4myt5YMZGrDYHnD8DbzUq1sEX4UJSgR99tByCtHQ8NDvXaGvwdaTBuvcqYfSKimRi/5b0aytlkUM7NeKG7jVjlV4WNCN/ZkUpREdHG5s3b67E4ZSNjCwbccmZNA/xKzUBojBWq5WNGzcSHx/Piy++yP79+/H29mbv3r1ERESUbyAxr8OqF3OV4DTwrC+JdPoltlt0x6AX4aqXKv66tZz//e9/PPDAA4C0jt26dSvh4UqdDkDTtC2GYUSX9fiaYt/JGVYS0rNo01D2wauLp+b8Rcz+MxgGeGs2Xvb+hAHZv5R+YrnR4Nb50OGmSri2oq5SVvuudeF6AH8fDzpdRN1yWloaAwYMYNeuXXnvdezYkTlz5pTfwYMkzOUF5wzIKS7sXgHEvg0Rg6VJTHi0tHSsAQlJ1cmSJUvyHDxAUlISJ06cUE6+lhPi70VIDQiHavmyyG8wfqZf1lIqJ7HcwFj9Csvtfdgal0r/yDCubFf9eQiKukGtC9dfCgsXLsxz8EOGDOGZZ55h06ZNxYvblEb0FMmqr4qSEq8A+HYkbPkUlj0Kse9U/j1rOPklhv39/VmwYAG9e/euxhEp6hIPX9uOBn5emNCZxHeYNb30ky4GzcwSbSiv/bSHhZtP8o/vt7Hx8NnKuZfisuOycvL566VjY2P5888/SUhIuPgLeteHKVth/E8iflOES3D+mvN/jQYN2kHXSZKJD5LIU7gs7zLk9ddfp0uXLgBcccUV3HRTxYU7k85lM29DHDH7kyjPlpai7tCsgR+LnxjEH9cepIFW0VE6zfXf5leyIfDmvPI8q01nW1xKBd9PkZ/DiRl8tz6OHcdTq3solc5l5eRHjx7N5MmTMZlMZGdnExMTU+7uZG6JvB5u+sbNB5fgHAxd5HHHLYRp+6HjreQ9GDx8od2oi792LccwDGbPns0NN9zA/v37AbDb7RV2/bTMHCZ+HMuHvx3g+Xk7+GL1kQq7tqJ2oWka3lc+gr3PE9iwUHHzPQMadYf7NsBdq+nfoSneHvI49rKYlDhSJXLg9Dnu+Ww9/11+gEdmb2bt/qTST6rFXFZO3sPDg5kzZ5KVlcXChaLDvmDBAtauXXtpF7ZmwB+VoNl+7hS0ux5+mAif9wH/xtDjfhj1P+jzaMXfr4Yzf/58brvtNvr27cukSZPYtGkTVquV+vXr889//rPC7rPjRBo2XSfHrpNtc7Bse3yFXVtR+ziZcoEbtgxiiPEDE/mYC0YFyZNmJXO+QVfun7GBl3/cRbNgX27p3Yy3JnSnR0slcVxZrD1wBqvdad86S7efru4hVSq1MvHuUvH09OT666+nX79+xMbGMmjQIF544QWee+650rvJuWPrTMgo5Ag8/KTnOg63p5QJkxn2/gB7F4oCXlocZKdBl9sv/po1EKvVyowZM4iPL96Zbt++nZ9//jnvZz8/P/79738zYMAAWrZsSUBAxXV5igj1Q8+t1fa0mJQa3WXOZ38cIjXHggGcoAlLuIab/TZB5iVs9QGYPPky5ih7T6VjcxjEnb3AiK5N6NVareIrk7aN/PGyiHqht4eJjk2rr0NcVXBZOnmQznKrVq3ihRde4I033uCll17ijz/+4Ouvv6ZZs2blu5jJQl4oXTODbwhkJl7iCDXo/YhECZxhf8Mhwju1nB07drBt2zYAsrKymD59Otu3by/1PG9vb5599lmioqLo27cvTZs2rZTxNW/gxxvjuvFt7DGaNfBl6tB2lXIfRe3AbBYpU4cBmD0xewVfuoPXTHDNG1w4YseeO6F06AbnrRW37aRwz4DIMB4bFsnvuxPpHhHEuD4tqntIlUqtrJOvaFasWMHEiRNJSEggKCiIP//8k6iocrQmsWXBV9fB8bVQr5Eo2OXvOFdeTJ7Q7+9w9asiF/tZL0g/IQ+GSX9AkzKXPtc4vvrqKyZPnoyuF8xUjoiI4I477sDLy33plMViYcyYMURGKpGZslJb6+RrGknp2Tw4cyPxqVl0DTrP++cm46Wfv/gLamYY+y10upWTKRe457P15Nh1/LwszHqgb40oH1TUfOp0nXxFM3ToUHbs2EGfPn04cuQI77//Pp9++mnZL+DhI01k7DlwPAbmjC7H3U1Iu7p8WDyl85ymgZc/PLhDWs/Wa1zzW8+WwieffIKu60RFRREdLd/P5s2b8/TTT19cYyCFopIJC/BmwWMDsdl1PDZ9AL/bi5hsuTB7QFMp9Wwa7MuixweRkJ5F40CfGt16VlE7uawS70oiNDSU5557DhAVtffee6/IarNULJ4QcRVEjZZVt08wDHsf2t8kDrowHn5Qvwl4BwKahP3NXtCklzR9cWL2gJDIWu/gATIyMgCYMWMGs2fPZvbs2bzyyivKwStqPB4WE3S/DxpeAWgQ2BKGfwQtrwHvwolyJvCsB426gdkLAw1DM4PZU5JnA10hYm9PMxGh9ZSDV1QKKlyfj5ycHB5//HE+/vhjAIYPH86sWbMIC7sI/WyHTZy2U5Vuw4fw25OuFrKNo6HbZDi2Svbdj62SzzxzV+5BERXwG5WPxYsX8+yzzzJ8+HBeeeWVYkPnJZGYmMiDDz5ITExMkc90XSclRep/d+/eTYcOHS55zIriUeH6SsSeI5N6Jwtuh53f5v6gQafx7Go8ni+PNSbH7mDLkbN4kk3zADOfPDwCb08VRFVcGmW1b+Xk3bBo0SLuvvtuUlJSqFevHp07dy7S01rTNEaMGMFTTz2FxVIGg02Lg+lXSP274YCbv4NfHpSmNoVjf6Ed4aFdbi9TWaSnpxMeHs6FC5JL0K1bN+bOncv27duZPn06VqtMTjw9PZkyZQq33XZbkWssW7aMSZMmkZRUfN2p2Wzm6aef5tVXX62cX0SRh3LyVcixNfDN8FxRLIOU29cz9qvTZNmKVteM6taE/xvdqeg1FIpyoPbkL4Ebb7yR7du3M3HiRFatWsW6devcHvfnn3/y7bff0rNnT6Kjo5kyZUrxJXiBLeChPRC3RnrPB7WCjNO43dzLrDhxBmeOgTNMXhyHDx/Oc/AtW7Zk69atxSa5rVq1ik8//ZQWLVwhx8TExLye7kOGDOHDDz8kNLSo/raPj08B5UGFok4QMRDu3wIJ26BZP05l1Mdkcl9/nZCeVcWDU1zOKCdfDE2bNuX3339n27ZtZGUVNcqjR4/y1FNPs3v3bnbv3s2sWbOYP38+X331VfGlXfXDofM418/N+sLpv0DXwZEt72lmGPR8iWNLSkpizpw5eU65OFJSUvj0009LdfD5eeONNxg7fjJ33fcAMb/+iLe3Ny+99BJXXnklmqYRGxvLCy+8wMqVK4ucazabefnll3nqqacuTm9AoahBxCVn8t7SvTh0g0eua0/bRqXkjYS2lxfQxteOj6cFm8PAMAxsDomYmk0adw1qXdlDL5HDiRlsi0ulY9NApQFxGaDC9ZfAfR//zurfl2M9d5bT6xdgO59KcHAwX3zxBTfeeGPpF7Blw46vJYTffjTExchefHiPvEMMwyA2NpbERKm7P336NC+//HLez2Vh5MiRjBkzBpOp5DzLyMhIIjv3YNxHa7HaHJyL28Hdw3vxyM0DCxx35MgR1qxZU0TTvXfv3pW2z75g43F+3nqKqPD6PDqsvUpSKgMqXH/xGIbBqLdXczbTimGAv4+FpU9ehcVc9lzl1Mwclu88TZCfJ12aBbLrZBptG9eneQO/Shx5yew+mcZDszblyfO+e0f3apfQtTt0Pvn9IJuPpjA4KoxJA1oV2R5VFEWF66uAhAtmgjtdBUDzntfi+PNT1q35ndGjRzN16lTefvttfHx8ir+Ahzf0uNf1c8exBT5OS0vjgQceKNBtzUl0dDRXX311qcbQvXt3br755jIbzfKdp3HoBjkOA++mndmQVNSZtmrVilatWpXpehXBpiNn+fC3A2TbHBxOOo+Xh5lHh7WvsvsrLj/sDiPPwQNk5Tg4n20n0M+z5BPzEeTnya35hFYaBpbwLKgiVu1JJNvm2iJctuN0tTv579bHMW/jcaw2nWNnzhMe5Mu1nd1UIykuCuXkL4EbezTl6z+PAVC/fijfLFvCZ9M/4plnnuHjjz8mJiaGuXPnlnl1a7fb88r2NmzYwMSJE4mLi8PHx4chQ4bg6SkPmIEDBzJt2rRKCYlHhPrhMPJJujau+HCe1ebgtUW72RqXyoDIUP42IgqzqfhJSFxyJnrumHLsOgcSyr79oFBcDB4WE1e2DWXLsRQwILJxfQJ8Pap7WJdM28b18fYwkW3T8fYwEVkJ9n02w8qLC3ZwMuUC4/q2YFzfiBKPP5SYgTV34mG16RxLugShIUURlJO/BO4Z3JouzYNIzsimf2QY/j4e/O1vf2Pw4MGMGzeOnTt30qNHD6ZPn87kyZOLvY7D4WDq1KnMmDEDh6NgNm50dDRz5syhTZs2lfzbCG0b1edfY7vw3fo4WobWY9q1Fa8wN3vtUVbuTSTHrvPLtlNENq7PDT2Kl6i9sl0o01ccxGzSMAyDm3uWU3ZYobgIXh/XlTX7k3DoBoPbN6wTIeRrOjXibIaVNfuS6NW6ATdFV7wtvbJoF1vjUnHoBp/8fpAuzYPo0KR4ffhR3Zuyck8imqZhGHBVx0YVPqbLGbUnX0mcP3+eadOmMWvWLDw8PEhKSiIwMNDtsQsXLszrhe7hIasFLy8vpk6dyssvv5y3gq8rvLxwJ79sk2Y0Jg3uHtSae68qeRKTlJ7N5qNnaRVWj/bhdbuhREWh9uQV1cGEj9Zy5EwmAL6eZl68qTODohqWeM7hxAz2nT5Hl2aBNKvGnIXaRFntWyneVRL16tVj5syZBAcHY7PZeOaZZ7DZbEWOS0hI4JlnngFg/Pjx5OTkkJOTQ0ZGBm+88Uadc/AAt/Rujo+HGT8vC76eFoZdEV7qOWEB3ozo2kQ5eIWihnPXoNZ4eZjw9TIT6OdJdKvS9/xbN/RnZNcmysFXAmolX8l89tlnTJkyJW+vferUqXlZ7larlR9++IGzZ88SEhLCihUruOKKK6pzuFVG0rlsjiadp13j+gSVI5lJUXbUSl5RXcQlZ5KQnkWXZoH4KHW/SkFl19cQ7rvvPqKiopgwYQJpaWl5krn5GTJkCF999RXh4aWvaOsKYfW9CavvXd3DUCgUlUCLED9ahKhVeU1AOfkqoH///uzatYvdu3dTeKXUuHFjbrrpplJr2BUKhUKhKC/KyVcR9evXp2/fvvTt27e6h1Kt7Is/xz++28Z5q50Hr27DmJ7Nq3tICoWigli5J4E3f96L2aTx0k2dy7Qfr6hc1PJRUaU8+91W4tOyOJdl4/1l+0lUOt4KRZ0gK8fOiwt2kpqZQ3KGlafmbC2iiqmoeqrUyW8/nsr0FQdYs6/iGrAoahfns+15/9a0gj8rajer9iYyfcUBdp5Iq+6hKKqBHLueJ1oFkG3T0ZWPr3aqzMnvOpnGI19u5suYo7wwfztLtp2qqlsrahBTrm6Lp8WEt4eZ7hHBtAxVHenqAj/9dZKXFuzgy5ijTPtyE3tPpVf3kBRVTICvJyO7NsHLw4SXxcSkAS1LVLJUVA1Vtie/5UgKdoeUkWXbdFbvTWJE1yZVdXtFDWFsr+b0axdKptVOq9B6mNRDoE6wem9Snia63WGw5WgKUSWonCnqJs+M6sC4vi0wm7RqbcSjcFFlTr5z80A8LCYcNh1vDzM9WwVX1a0VNYzGNaBRh6Ji6dUqmC1HU8i2ObCYNTo1c6/uqKjbaJqmonM1jCpz8t0jgnnlliv4Y08iVzQLLFGrXKFQ1C5u7dMCLw8zO06kMbRjI7q2CKruISkUCqq4hK5/ZBj9I8Oq8pYKhaIK0DSN0dHNGF0JDU8UCsXFo0roFAqFQqGooygxnGok9uAZYvYl0bVFENd2blwnWlkqFAowDIPFf51ib3w6Qzs1okdLJQqjqB6Uk68mNh85y7PfbcNq01m6PR67w2BkN1VtoFDUBebExvG/lQfJtuks2R7PJ3f1UtUGimpBheuriW1xqeTYXCWF6w8lV/OIyo5hGBxPziTpXHZ1D0WhqJGsO5ScV1JoGLCjFgkE2R06R5LOk34hp7qHoqgA1Eq+mujeMpiv/jyK1abj7WHiynah1T2kMmEYBs/P20HMgSQMAx69LpKxvZT+vEKRn/6Roew8kUq2TcekUWuqDbJtDu77fAMnz17AAN65vZvaaqjlKCdfTXSPCOat8d2JPXiGK5oHcVWHhtU9pDJx4uwFYvYnYbXLKuW/yw+Uy8knZ1g5euY87Rr5E+Cr+sgr6ia39m5OgK8H++LPcVWHhkQ2rl/dQyoTsQfPcDLlAlk2ByD2/cX9ZW+qdeKsRPg6Ng3E28NcWcNUlAPl5KuRXq0b0Kt17Zol+3iayS9H7etV9q/Qvvh0Hpy5CZOmYdLgyyn9CA9SwjiKuoemaQzrEs6wLuHVPZRyUc/LA6eBaxr4e3uU+dzlO0/zyo+7MJs0Gvh7MXtKX3w8lYupbtSevKJchNb35vFhkfh5WQjx9+Lft3Ut87nfrYsjK8dBptXOBaudZdvjK3GkCoWivPRsFcyo7k3w9jDTMsSPp0d1LPO5M1YfxmrXuZDj4GyGlU1HUipxpIqyoqZZinIzpmfzi+oDHxbgjafFRI5dx8NiIrS+VyWMTqFQXCyapvG3EVH8bURUuc8Nq+/NieRMHAbohkGIv7LvmoBaySuqjLsGtqZ/ZCgh/l4MvyJcNShSKOoQz4/uROdmQYTW9+KBIW3poEoGawRqJa+oMrw9zbx2a9nD+wqFovYQWt+bT+7pVd3DUBRCreQVCoVCoaijKCevUCgUCkUdRTl5hUKhUCjqKGpPvgKJ2Z/E4cTz9I8MpU1D/+oejkKhqCAcusHS7fGknLcy7Ipwwup7V/eQFIoyoZx8BbFg43E+/O0AOXYHs9YcYdYDfYgIrVfdw1IoFBXA6z/tZvmu09gdBt/GHmPBowPx81aPT0XNR4XrK4gVuxLItjnQDdF333z08hWCOJ6cyZajKVhzpTEVitrOmv1JZNt07LqBzWFwMDGjuodUbeyLP8eO46noulH6wYpqR01FK4huEUHsjU8n26ajaRAVXju0qiuapdvief3n3Zg1jbAAb2Y90FdpWCtqPR2bBLDpSAo2h45hGDRv4FvdQ6oWPli2j4WbT6BpGr1aNeD1cV3RNK26h6UoAeXkK4h7BrfBx8PM3vhzjOzWhI5NA6t7SNXCjNWHsOa22ExKz2brsRT6tq0dHfYUiuJ4+ZYrmLHqEMkZVib0a0lwvctPzU3XDb5bfxzdkBX8uoPJJGdYCVX5CTUaFa6vIMwmjYkDWvHabV1rTdvYyiDU3xtT7sReSVu6WL58OePHjyciIgJN03jppZeKHJOTk8OTTz7JgAED8PHxUSukGoSfl4VHrmvPv26+gvaXaZTOZNLw93GtCzWT/F0UwqJFi+jcuTPe3t506NCB7777rsgx6enp3HXXXQQFBREQEMDtt9/O2bNnK3VcyskrKpSXxnamU9NAQut78dA17Wjb6PJ8IBZm2bJl7Nixg6uvvhpfX/eh3gsXLvD555/j6+tLv379qniECkXpvH9HD1qG+hEe5MPrt3UtVxfKuszatWsZO3YsV111FUuXLmXkyJGMHz+e3377rcBxt956K6tWreLzzz9n1qxZbNq0idGjR1fq2DTDKHvyRHR0tLF58+ZKHI5CUTfRdR2TSebUISEhPPzww25X84ZhoGkaH330EdOmTaM89lkYTdO2GIYRXdbjlX0rFBfHddddh81m448//sh7b8SIEZw7d461a9cCsG7dOvr168fq1asZOHAgABs3bqR3794sX76coUOHluueZbVvtZJXKKoAp4MvjbKE6H/66Sd69OiBn58fQUFB9O7dm9WrV1/qEBUKxUVgtVpZuXIlt956a4H3x40bx7p160hPTwdg6dKlNGzYMM/BA/Tq1YuWLVuydOnSvPcq2r6Vk1coahGHDx/m5ptvZsiQISxevJhvvvmG66+/npSUy7dkU6GoTg4fPozNZqN9+/YF3o+KikLXdQ4cOADAvn37ihzjPG7fvn1516po+1YbKgpFLWLr1q34+/vz1ltv5b03YsSIahyRQnF5k5qaCkBgYMGKqqCgoAKfp6amFjnGedyRI0eAyrFvtZJXKGoRnTt3Jj09nUmTJvHbb7+RmZlZ3UNSKBQVRGXYt3LyCkUtIjIykkWLFnHkyBFGjBhBSEgIEyZM4MyZM9U9NIXissS5YnfuvTtxruCdnwcFBRU5xnmc85jKsG/l5BWKWsbIkSOJiYnh7NmzzJgxgxUrVjBt2rTqHpZCcVnSunVrPDw88vbVnezbtw+TyUS7du0AaN++fZFjnMfl36uvaPtWTl6hqKUEBAQwYcIExowZw549e6p7OArFZYmXlxdXXXUV8+bNK/D+d999R9++fQkICABg+PDhJCQk5JXUAWzevJkjR44wfPjwItetKPtWiXcKRSUwe/Zs7r77bg4fPkyLFi2Ii4tj06ZNgCjb7dmzh/nz5+Pn51fAwJcuXUpmZibbtm0DYP78+QD07NmTFi1a8Omnn7Ju3TqGDRtGeHg4Bw8eZN68edx5551V/0sqFJcphe37+eefZ/DgwTz22GOMHj2aJUuWsGTJEpYtW5Z3Tt++fbn22mu58847efvttzGZTDz99NP0798/r0a+UuzbMIwyv3r06GEoFIrSmTlzpgEYR48eLfBz4VeLFi0KnNeiRQu3x82cOdMwDMOIjY01RowYYTRu3Njw8vIyIiIijKeeesrIzs4uMgZgs6HsW6GocArbt2EYxsKFC42OHTsanp6eRmRkpDFnzpwi56WmphqTJ082AgICDH9/f2P8+PHGmTNn8j6vDPtWincKRR1FKd4pFHWXstp3uZy8pmlngLhLGZhCoagyWhiGUeZuScq+FYpaRZnsu1xOXqFQKBQKRe2hXIl3ISEhRkRERCUNRaFQVCRbtmxJLs9KXtm3QlF7KKt9l8vJ/z975x0eRdn14Xu2pRdC6L0IASK9KU0REQSl2FApiiCIYH99sWDFggWVV0HRDxRFUBErCiKCVOlIbwmhJpBCerLZ3Znvj7PJ7qZQN9kkzH1duZLdncw8m+wz53lO+Z2GDRuix+x0dCoGiqJclOtdn986OhWHC53fep28jo6Ojo5OJUU38jo6Ojo6OpUU3cjr6Ojo6OhUUnQjr6Ojo6OjU0nRjbyOjo6Ojk4lRTfyOjo6Ojo6lRTdyOvo6Ojo6FRSdCOvo6Ojo6NTSdGNvI6Ojo6OTiVFN/I6Ojo6OjqVFN3I6+jo6OjoVFJ0I69T4cjKtXMwPp3cPIevh6Kjo+NlUjKtHErIwO5QfT2USsFFNajR0fE1RxIzGfvZRlRVw99i5Itx11At1N/Xw9LR0fEC6w8l8szCHRgMCvUiAvl0TBf8zEZfD6tC49OdfE6enW1xKcSn5vhyGDoViK/XxZGVayc7z0Fato1ft5/09ZB0SiA1K4+tR1I4m5Xn66HoVBA+Wn4Qq10lJ8/BiZRsNsUm+3pIFR6f7eQzc22MmLWetGwbqqbx+p1tubbZBbe+1rlCCQs0YzIq2BwaJoNCSIDZ10PSKYZjSVncP/ufgsefje1Co2rBPhyRTkUgLMCMooCmgapBiL8+vy8Xn+3k1x1MJDXbRnaeg1ybymerDvtqKDoViPt7NqF1/SoEWIxce1U1BrWv6+sh6RTDj1uPk221k2W1k22188Pm474ekk4F4PnB0TSKDCLQYuTOLvVp26CKr4dU4fHZTr5qsB9o8rPRoFAjLMBXQ9GpQAT5m/jovk6+HobOeagW4o/FZMBqV7GYDFTX8yZ0LoDaVQL5emJ3Xw+jUuGznXzHxlW5t1tDqgZbaFM/nP8MaOGroejo6HiZ2zvX57qWNYgIttCrRXXu7NrA10PS0bki8Wl2/ZjrmzLm+qa+HIKOjk4pYDYZePm21r4eho7OFY9eJ6+jo6Ojo1NJ0Y28js4FoKoamqb5ehg6OjqlQGWe37oYjo7Oefhp63HeWbIfgwJTBkfT5+pavh6Sjo6OF9A0jfeX7ue7jccI8Tfz3ogOtKwT5utheRV9J6+jcw5y8uy8s2QfNoeK1a7yyo+7caiVc8Wvo3OlcSA+nZ+2nkTVIC3Hxqs/7PL1kLyObuR1dM6Bqoowh+tx5XXr6ehcaeTZVRTF83FlQzfyOjrnIMjfxH09G2M2KpiNChP7Nsdk1KeNjk5lILpuOJ2bVMVsNOBnNvD0wJa+HpLX0WPyOjrnYcz1TbmjS30URSFUl9HV0ak0GAwKb97VlpTMPAL9jARYKp9JrHzvSEenFAgLtPh6CDo6OqWAoihUDfHz9TBKDd3vqKOjo6OjU0nRjbyOjo6Ojk4lRXfXX8HY7NL9b/+pdAZ3qMv1rWr6ekg6OjpeIi07j4+WHyQ5M4/7ezUmum64r4ek4wN0I38FM2vFIb7fdAyrXeXfY2epFuav3wh0dCoJz3yzg53HU7E7NLbFpbD4sZ5UCdJzS64012l3cAAAIABJREFUdHf9Fcyu46lY3epCDydk+HA0Ojo63uRQQgZ2h2g6GBQ4eTbbxyPS8QW6kb+CGdC2Nv5mI2ajAYOi0KlxVV8PSUdHx0vc0Kom/mYjfiYDgRYTTauH+HpIOj5Ad9dfwQzuWI9aVQKIO5PFNc0iqRMR6Osh6ejoeImnB7akQ+MI0rJs9Imuib/F6Osh6fgA3chf4XRpEkmXJpG+HoaOjo6XMRgUbozWmyld6ejueh0dHR0dnUqKvpPXueJIyrDy3Lc7OJ6Sze2d6zO6VxNfD0lHR8dLHEpI54VFO8my2nnkpub0ucK9GfpOXueK482f97D7RCopmXnMWxPL9rgUXw9JR0fHS/zn6+0cScziTLqVV3/YTUqm1ddD8in6Tl6n3KJpGnNXx7JiTwLtGlTh0ZuiMJsuf12amJGLw1k5qCgKKVl5l31OHR2di8NqczD9933sPpFG/za1Gd6tkVfOm5ZtK/hZUSAj105EcOXVpj8f+k6+jNA0jSU7TjJj2QH2nUzz9XAqBH/uSWDemiPEnM7kl20nmbc21ivnHXN9U/zMBgItRqoGW+jaVE881LlMbLmwfjr8+QykHvX1aCoEn/x1mN//jSfmdCafrYxh3cFEr5x3VM9G+JkNBFiMtKlfhXpXeNWQvpMvIz5fHcsXa2LJtaks3nycL8ZfQ4PIIF8Pq1xzIjmbPLsDAKtdJfZMllfO26N5dRZO7E5Cag4t6oThb9ZLi3Quk+/vgcO/g8MG2z6DR2PBT69LPxdHzmSS5xTjcqgqx5OzgGqXfd77ejahZ1QNsqx2WtYJw2BQLvucFRndyJcC8fHxTJs2jR49enDbbbcBsPZAIjlWGwmbfibn5D5Grq3CM4+Np0uXLrz22mscO3bsoq4RGBjII488Qvv27Yu8tnr1aj799FOsVolF+fn5MXbsWHr27HlB5/7uu+9Yv349kydPpkaNGhc1Lm/Su1VNvlx7BABV0xjaqa7Xzl0rPIBa4QFeO5/OFc6RFWDPlZ8deZB0AOp09O2Yyjl3dKnPtqMpGBUFg6LQM8p795rG1YO9dq6KjqJp2gUf3LFjR23Lli2lOJzyS1paGp999hlnz54953HZ2dl8+eWXJCUlATBw4EDatGnDtiPJrP17JRknD3htTGazmVGjRnkY4qNHjzJ//nwK/18VReG5557jxRdfxGQqfm2XkZHBxIkTmTdvHgCtWrVi586dGAy+i+okpOaw83gqV9UMoVE1feJeDIqibNU07YItzZU8vy+b+QMgdoUYeP8weCxOvl8oeVmwdxGYAqDlbWC4MrxLh09nEHsmk7YNqlA91N/Xw6lQXOj81o28E1VVWb58OWfOnCnyWlpaGtOnT+fIkSOXfZ2QKpFMePQpyDnLu+++i91up2PHjkwcP5YAeyoEVQdLMTGkjR/CyU0AaAGRLLN3Z+5X3xR7DUVRmDRpEt26dQNg7dq1fPjhh2iaRpcuXRg7diwWi2ejivT0dN577z1iYmI8nn/nnXeoXr16wWOLxUK/fv0IC7uIG5iOT9CNfClwbD388qD8fMtsqH+t/JyXDevfgexE6PIIVL3K8/dyzkqsPjIKzIWMmeqATzpAymF53LQ/9P8AAiPBpDeU0Ske3cg7OXjw4Hl331lZWbz99tssXbr0nMdFR0dz++23YzS6rbIzEiDrNFRpBH6hsGkmjcwJ3B2tcTAZfjxkwV6zAzTtT2DeGYbXjaF6ZAT0nsqOo6ls376d4TdEY/7yOtkFGC0w5h+ocbXnxV/1B4ezFEQxgmJgZZzCurC7oGqzgsMURaFPnz506dLF49dXrlzJ8OHDOXXq1DnfY5s2bViwYAGPPvooy5cvL/aY+vXr89Zbb9GwYcNznstkMtG6dWvMZvM5j9MpHXQj7wXiVkNmvBhecyBMi4C8/EZOCvhXgT5vQPsxsG8xbJ8r94IbXnPt5HcugB9Hys8BkfDwbgh06xNxNg4+agn2HNdzBj/wC4L710D1lmXxTnUqGFe8kS/ser4QwsLC6NevX7FGqVXLljx+Uz381CxodScEVIEDv8KiuyTZRrVD035waous5t0xB0GTm2D/YucTCoTUhsePARq8FgyOXNfx4Y0gsrms8G96Vwz+zNaQuBc0R6FB14dHYuBsrNxwdi+QxUC7ByAwwuPQ5ORk3nzzTRISEop9/1FRUTz55JP4+/uTkZHBW2+9RVxcnMcxmzdv5sCBCw85REdHs3DhQlq1anXBv6PjHXQjfxHkZcvcMVqg1V2yg179Gqx5HezOEsv2D8D2/5O57o7JH2q2hRP/yGODCRr1hhHLxIB/0Bhwu8826iNzNLgG9P+fbA7erQ3WwlU3CjS7Be5YCGnH5Tq7vpbj24/Rd/lXOFe0kd+yZQt33303hw8fxmQy0aZNG9fuW1MhJUZW435hUKUxKAqNGzfm7bffpm7VIECBgEJ91X+8H/Z8J78fXAsm7oUFgyBmmedxfmGyI3dY5VgQI2/LAVxtXTGY4Olk2P0N/PpgMe9CATQIiICnTou34Pt74OgaPG4YVRrLjSntuCT+GEzyemg9mHTA67G9vLw8Xn/9dZYuXVok7l+Yw4cPk5KSgr+/P++99x7jxo1DUa7cTNdcm4M9J1KpHupPvaqlX1lxRRr5jHj49g5IOQQdH4LrX/J8PfMMWII9Q2KqCrM7QvIBQIEGPWD47/BObdnFuxNYHWxZ8pWPyV/musNNbyEwEp5OlLHsXVT8WA0mqN0RxmyA+O2w6G5IPohrfivQ9CY4uVnuH45c8eIZTNDkRrj7p0v7G+mUCmnZeRxMyKBxtWCqhpR+Xf6Fzu9Kk12/e/duHnzwQQ4ePEhycjIArVu3ZuHChbRo0cJ14N9TYc1rYLeDMQOuuRH6vCavrX4d5r4sO+gqTSB6GPSaAkaTGPj8iZ1+HE5therRklXrvrK3pkG1ltD2flj5ghjZkNqQcsRl9AFqtpMSm/TjJbwj50S3ZoI1HULriDfg2FrQ3G4Cda8VN6Hd2Sva4dzpp8bBmT1Qs7U8PnsEMhPkpmK8dPe5xWLhpZde4qWXXjrvsZmZmTzyyCPMnTuXhx56iCeffJIaNWowZcoU7rvvvivK4Gdb7Yz8eAMpmVYcqsaUIdFXvNxmqfDLODixETQ7rJsG1VtBqztkziwaBvt+kJ9rXA2dJkCHMbKATtrnyo4/vFR271WbyZxxX1Rnn5Gdfkht2DxTDG6t9nBik9sgFGghVTVkFs3xEXkSVe4bSU6vWK12ENHEudBwYrTIsTkprjFoKqg2OLhExpi/mz+9SzyKtdqJAoxOmXLqbDajPt6Aqkkl0Kz7OxNVO9TXwwIqkRjOqFGj2LBhA8nJyRgMBiZNmsTGjRs9DTzIyty91GXdW7Dza8luXfWSPKc5IOUgrH9bXHZn40Bx+1OpNjHgvafKhC9M4j645gno9SI0vA76vgu3fQWWUDAFwlUDIaQOrJ4KUYPA6F7KpcjiwRwE5mCo11VCAwCNb/BcKKDBnm+KuvBBnvvjSfn53y/ho1bwZV/47BqX+9GdY+vho2iY0Ry2zRH35WUSHBzMnDlzWLBgAeHh4WRnZ3PkyBFGjx5Ny5Yt6d27NwsXLrzs61QEthxJISXTSnaeA6tdZc7fMef/JZ2LJ+OUGHiQeb54BJzcIrvhg0tk7mp2SNgOSx+FA7+IZ89jTijw9ytwxzdQv3vRa8Qsk5h7x/HQpC/0nwE9n5XMeL9wiBoCWWdkHnWZ5DTW+ac2Qkgt5/wOgrajXK816ed5HYcVYpfL7xRGU2WMAMuegs+6wtye8MOooseC3OPebwwfd5Awo8Ne/HE6l8Tv/54i22ony2onJ8/BdxvLjyBShTbySUlJTJ48mREjRrBt2zZAYsapqanMeOdN/LNPFv0wd3pYEmjy0exisDfPxGPFDpIIs+db+KCRW7KNk/htkiV721fQ/8NCI9Nk8bD6FTjojNuHN4Bn02DMeoj7Cw78CGvekBjb9S+D0c/1u35hMHgu3PopjFjuWpnX7QLGwpm5Nggqob709E75vvIFeS95meIOPLa20DkcML8/JO6Rxc3PD0gcMf3cSXoXyrBhwzh9+jSnT59m9uzZBAUFsX//flauXMndd9/N+vXrvXKd8kzVYAuq8+NlVNDLhS6XnFTJVi8cMrr+ZWfIyonDCitflHlcOJZuy4W/X4W5PfAIpaFB3CqJmY9eLXFxdxQj/DAStn4C+38Q49pxPDyfDQNnQcxSef73SXLNqCFup1Zllz9gJtzxLdw03fVay9s8xy4XEy9eETTJAXDY4Z/3wZYtnsY930BWkuehqUfh5zGQegQStsHCQfBpZ3n/Ol4hMsS/QHLbYjKUq/ldYY28w+Hg+uuvZ9q0aXz11VcADB06lI4dOxKSHQfv1oFZreXLmgF2q7jx/EJh2E+eq+uzMfDns567dZAJl3Ko6MUNZmg2wPW48wTZfStGOW/r4eLGtzl3w6pDrg0Se8NptO05EmOv2do1uQ1mCK0rLsarhxVNrunzhhyTj9EPrn0CBn7s+Z4AspOl9C6ohuu9qQ4p03PHbhVPhjs5ybB9jtxEV74M79aFL2+C7Etr5mKxWKhevTpjx47lyJEjrFmzhpYtJWv4jTfewOEoxhtRiWhVN5yx1zelWogfV9evwvODrz7/L+kUz4FfJFHtwyhYcKvE1HPT4fgGqNsV+rzpORcO/wb/fFDU42UwwqnNRc9v8oeWt7se3/a1JLXmz++ez8m8zfcIKgZJigVZQOfPe1s2HF8voTmTv+vcVRpC25HQ7GZP13pobbj6Hk9DbzDCkC+gw4Oe8x7knhKzDCxu+R2K0fMxQOZpz9wcTZX7Wuxy8WAsHinz+8fR4vLXuWgGtqtDv9a1iQzxo0fzaozq2djXQyqgwsbkU1NT2b17NwAff/wxtWvX5uabb5YX/5oC1lTngXGw43PY8jGkHROD1rCXuNWy3eJlmh0cUJDwBkVX/iCTqPercM2Tbs8pMG6bxPKMFmh8o1zv+HqZ6AajXBOgQU85XjHKhI++S1x+XR6VzN1qLeDm/5X8xq95DKIGS3zx1Ga5ceWmwnUvyuu/P+oqtdMc8OdkuOUTWP+uuDJ7PAM1ouV1h01uAMG15Ka2x63uXnWAfzjE/ilhC1uWuCB/nwS3zT/3P+c8VKtWjWrVqjF16lSGDh3Kr7/+yujRo/niiy8u67zeJttq52BCBnUjAon0QiLNvd0acm+3hpc/sCud3ya5ys2OrIQDP0ntuiNP5nezW1y5KflodpnWisnlzi9ufptD4NZPJB8nH79gEbeJ+UMW4PW6Sgx890KZa4oCNZy5L1GDYcdcGYfJD5rfKol8CdshbiU07iPexJIY/LncCxYMgsxTMsacFFnEG8ywdbZ47wBsmfDdnTB0voTmHDaZ62Zn+C8vW3KEaraVKpz8hQhIIp9/Fdj4gSQG2nPk/dRsC10fucB/RMXmbFYeR5OyaFojmGD/yyvzNRoUJt9aPiuIKqyRd6dz587UrFnTlUFvCXZNZsUgMbe04+KuBjFcxWGwiGEsLsYNEFAVxm6BiIZFXzOaofktEv9+v4Ec2/t1WUg0HwQ128hxEY1h7CbY/6MIY0QNlptEn9dcCYDnwz9MwgWaKl+rp0KP56D9WDi8TM5dEHrQZMcxfpvnOY5vEDejapebR/dnC11Ek/e0+jXXTUW1ebX5xpAhQ/jpp58YNGgQ8+bNY+bMmQQF+U7PX9M0kjKshAaYyc5zMGLWenLy7DhU+GBkB9rUr+Kzsem44R5uQ4OY5SI2kz9v95WQzZ4fEisI4RVy9VdrJZnuxWnO+4eKO/2vKfDNEEmu7f0q5KZB2/tc5apN+sDwpbLTb9BDvkDK4C4ERZH7lDXVNb+XPQkthogX7+hqOLPL7XiDLDweLZTjsfUzp2iPBv4R0OgGTyOvOaTsdscXrgWTPfccicAVH7tDJSUrj4ggC7FnMhk/ZxOKomAyKswbfw01wiqnzHWFNfLBwcFUr16dM2fOFOi3v/LKK0yZMgVufEvcWNlJsrNu1EeaRpyL0PriIj8bKyv2ghIZRcrYHouTFf25SD0m2b32HEg/KTG7iXuLHlethXxdKkY/8Q7kG1+jRSa7wQDDFkvCz28TZZdhy5YxBUZKkl8+P4xy7WRUG+ych4cXQzHA0sedNwDFdc2ez136uIth4MCB1K9fn2PHjtGxY0cWLlxImzZtvHqNCyHPrvLw55s4EJ+B2WhgSMe6ZOTYsDobaHyxOpbpwzuU+bh0imHIPJjTQ0rKQuuJcTZaPMVkANfnWRGj3HoE7Jovczx/fhvMUnFy30rZeZ+Lw8uc8e8sCYUF1YDbvy56nLtxvxT8Qj0TbP2cWdp+ITB+hxj9rZ+IUc7LhLm9YNxWqBbl+p3fJlIwl3NTpLrGHZM/LHnIFVowB8n8bj/m0sddjknKsPLA7H9Izc4jPNBCq7phZOfJotBoUPj933juK0cudm9SYWPyFouF253NX/J5++23sdlscGyNGHiA3LOw8nno9p+iWapRQ6Df+zJxnjgKN70Dd30Po9fA8GXyerNb5PH5DDzINQtiX5qU5pQGlkBx6/mHi8fgzkVi4PNpPxq6/dd1o9Ac8O2dnuconH9gCYYO4+SmZw6ClneJyz7/vVSPhgm74ar+Xn0rBoOBX375hRYtWrB//366dOnC7NmzvXqNC2H1/jMcTpCuWFlWO+sOJhaU+JmMCtVCr9x+1D5DVYt/fvtcl3hU8gFI2AEthhY6SJEKl/4zZIH+8G7o8V94cAuMWgF3LpYwWfQwqTc/n4EHZzld/thspbfrrdUWrn1a5mF4Qxj6les1gwH6vwf1e1BgxO3Z8PVAz3MULqOr3R4aXi/x/oBIqHuNy8CDhOsmHRIRrkrIN/8cJSnTitWukpRp5XRaLmaj/I3MRoUqQZVXWKhC7uTT09IYd0s7Fq5xrU7DQ4P49LG+mBO2wOE/PH8h5ZDErLs8CvNukNrUhtdJQk1hHWlFkVpTgKZ9L25gNdtAjTZw+l8xkD2fv/g3d6FE3yVfJWEqnIVfqGzutvlSTqfaxLAPmSc3ly4TZWew7zs3I49k5eeHO0Dqgle9JB6Cvu9AcKFkvougdevWbNmyhccff5zZs2fz0EMPMXjwYA/N/NImf8KDfASqhfjRsVFVlu+O56qaITx8Y+W8+ZVL8rKl2uPoGqlzH/4HHFoiIbc2w8Vl7c7JjTBhp8y3r/pJ0mi7B6Dv20WNnckiVSoALYdwUUQNkkoVxSAL555TLv09no/rX5SvktAK5RNkFKqEueVTqQDIF9S6YSoEVYODv8G3tzv/hkaciUhw9G/Pv9XexVJxVKM13PB60ftkBcNiVArenqJAh0ZVqBJkYfeJVLo1q8aAtrV9O8BSpEIq3v133N28NXshZgN8eguMbGtAyS+BMQdC3W5wxE13PWooDPu+bAbnsMtNJyDi8lzyl8up7TDbrQ2tYoQXC90YVFXK7P6cLDeJ3q/KxI5ZDmhFcxTqdIGx/zi1tlu4FPZqdZDnvUDt2rWJj49n5MiRfPrpp0Ua6ZQWDlVjyqJ/Wbn3NNVD/flwVMcyUaUrTSqs4t0/H8hn0p4LGJxed+f8toTIwjLVzf3cdzpc+3jZjM2aCfFbRXo6vH7ZXLM4/vkAlj7mehxaF54o5Flw2KUU8C/nZmPAR/D1LS4Vv3zPpuaQedxhPAz4HxxaKmV2jjzZLLS9HwbOLPW3VJpk5tqY+MUWDpxKJ6p2KP8b1fGyk+18TYVXvFu+fDm//PJLEelUTdP4aLYksbzZB0a1BY8aV1u2p4FHkZrzssJogvrdyu56JVG9pQjuZCbIBG7cp+gxBgMsmSDd7TSHyGrW6ex6XVFkl293Gnl7rtzk/u9aV/mQapf6+rjVcOQvee9NbrzkYb/55puMHj2aefPmsXnzZnr37k3z5s0ZP358qTa6MRoUXr+zLaqqYTDoimE+xZHnFpNWPfPj8jI8PUrm4LIz8CBhu/xKGV8SNUSMd16WGOJ2DxQ9RjFI9n2us0HXvD4i2FPwugIozoW8KjkNKTGSWJgv0WvPFa/d3u+loiBqsHj8KhjB/mY+H3fNFTm/y4WRT0lJYfHixeTmiuHYtGkTX3755Tl/p3aogfvagtwBzuGNMPldWLytsmHyk2Sc7XMlYaekhJqzsa6dusEk9bhJ+yW/oEFPQBO3qcEEN38odcBWd2EgReKDX/WTG4I5AG5fKJUGl8DIkSNp1qwZ99xzD/v27WPfvn0AfPHFFwwfPhyTqfiPrMViYdCgQdSoUYIw0AVypd0AyiVhDSXR0+GgwJ3sgdt8D7lCpYHD60uVzp5vIeIquPruosfYc0QSO5+8TMnl+f4eKfHr8KB47dJPSHJfz+flfO618opRKoJ+GCUbqPXvSF6De5JfBeJKnN8+M/KZmZls3LiRY8eOMWXKFE6ePOnxuslkYsKECTRt2tTzF3PT8F83laHNrEQE+8nO89QWiS0XrnsNjIRbP7syjTyIYlePyec+pssk6bSlODX2WwyVG0a+wdY08Qb4h8vjM3sp8JwoBohsKRnO+ZnNtmwp4btEIw/QtWtXtm/fzvfff09CQgKzZs1i69atbN269Zy/9/zzz/P555+79BIKoaoa/xxOIs+h0u2qagUKVTrliGPr4MdR8nkyBUjpV+wfMrc1twW9YpDa7zu+OefpKjXVWrj0MYrDEiR1+rFOz2aj3pJX8Ey6GHKzv+TdZCaIQJbRLG1yTf5SQWBwlgWnHnWrNtIkfl8OjXyuzcH6g4kE+Zvo3LjqFdUb41z4JCZ//PhxevTowdGjrprr1q1b0717dxRFwWw2M2LECCmNW/kyrH9LPoT3/i5NJ3Z87jpZSB14eK8IRnx/r9SQaip0HCdtWnXOz7H1UgnQpG9Rtax8VAesfVNuwuENZEfvFwrxO5w3YLv83c2BMGCWKHp5iZSUFGbMmEFSUlKJx2zcuJH8z+Zrr73Gs88WrvuHFxb9y5oD0ga4ec1QZo3uVKlvBOU+Ju+wy67y4K9S4nbv7/DljZK4ms9VN8PgL8Tl/EVvqUvXHCIO02ZE2Y21oqI6XDk2TfqW3JXSmgkrnpVch8BICeEFRIirXnOIa1+1y/y+fzXULl/lpHaHyn2fbODk2RzQ4Jb2dXjiZh/mRJUB5TomP2/evAIDf+ONN9K7d2+eeuqpoq7Yk5tF/11TRbluTndnRyY3rrpZhCr8Q+H+VRC7QsrBykNcvKJQ/9rin89KhC2fyN8/cZ/o7dtzpSb5rsWw4jlX9zuDGep1E2EQL998IyIiztv1TlVVpk2bxrPPPsvUqVOLGHlV1Vi+O6FA6nzvqTQSM6zlSmP6imPrbGcbVk2S2T7rIvO8AEViwEGR8jVhj+wiwxtKFzmd82MwwlX9in8t6QDs/Erul3sXSymimiehkof3wcxWrqoczSCiXp0mlDsDD3A0KYuTZ3PIcda+/7ztZKU38heKT4y8zSYxnylTpvDKK6+UfOCprZ6iEDnJRY/Z+ZW4oJoNEHdTSR9onYvDYZMmFuknXaI7Ba/lwa8TPBtnqDYpVWx+q2cpTr5VLeUds8Fg4D//+Q/PPvsseXlFu+wZDArVQvxIzLCiaVIyFxpQsbNrKzzH1uARX3fPmAd57a8pUtNdI1oW8pcRBtJxIyMeZndyJjEW8uY6rPD7RAlzFggMqZCdCI2u9zy2jOb3+YgM8fMYSu0qlVO97lLwaVDSYDjP5RvfUEi0pZgPkj1H3PSViZxUWDBYWkOuft03Y8g4JVr1hQ28++taIbGSrERR4srn8B/wRhhM9Yf10/E1/xvVifYNI2hdL5wZIzviby7BdalTNjS7Bc85Xcz8zjrtlGetRKTEwv91gxnNYM93vhnDqS1Ow1xCuPboGrfOmE7it4vqXz4bP5S5/UaY1N/7kLBAC+/e246WdcLo0iSSd+9tf/5fukIoF9n1JRLRFG58B1a/KgbFlu2UbzVKdmh+VnhxjSYqMsseh0O/i6tszetQp5OUpcX9LYa3af8LU+C7HIJrSU2yLYdibwSWwKIdvDSHp67493e7WvSueFYS+nyYDd0gMoiP7uvks+vrFKLVXdK0Zc+3Mq9zM8Bklt2horjKNPMbLlUWvhnqyh36YZR0zgupDYd+AxRRlSwpdu4tarT2FLtyRzFJom1hRT+H1dX8JisJ/nhKvHqOPJnrz6SV7pjPQ4dGVZnzYFWfjqE8UuZGPisri8WLF5//wLQT4i7OF27Ix+gHt/6fJIZs/ghQROShMpES66ZQp0n3vJUvSic5RZEbwvh/S1eFymSBsRth7TQ4s1vidw6rlONVuxrqdpbGOO4YzCKNC5LI4y6bqSiu2lsdnROb4IvrPT8jAKYwkZn9+xVRZTOaof85ujJWRNJPuLxgBqNkt/86AY6ukuca9oZ7firdMYQ3EL3+TR/BmT3SbhvALwwadJcFwO4Fnr8TXEsy9AEyTno28tLndrmlTI28pmn06dOHXbuki9KgQW4NU5IPidE4sweaDZQEnMIGHiTpK6Kp9Frv+ZwYFv/QsnkDZUX3/8J3W2RFbQ6QOPdHLV1lLBnx0oWupIQ5bxHeQJSuTm2VjnW2bNldNYiATg/B5lmSJ6E5ZKz3LpEdvjUTZrV2nUcxQtvRcr4ywOFwcPjw4aLllzq+49h6WPOGfF7aPwAbZxQ18CDd1+p0ghHLpA2yf5hr91hZuPYp8U4qRqh6FVRpAjFLXR7JQ0tkDpW2t65OJxjyuXSiWzJB/h8OK9TuJInLB352/o80sITCyD9lsZ4SK9LX+aFUgwn6fVC6Y9W5ZMrUyKuqSnq6S5whMNDp2j17BGa1cSV5nN4JYfWKnkAxyQp4+xzJsA2KLP1BexPNKSyDJgIyJeUkNLtZmuYkH4J610JAOFRp6mqnqdqL//uUFsmHXBPaYZVYh04xAAAgAElEQVSdfXANmHRAJHxDakPV5rL7B8mAzk5yuVvD6sPA0ve2GI1Gunbtyj///EO7du2YOXMmI0boZVY+J3YFfNXfld8Rv9XVWc0do0V6nK95A7pPhpCaZTvOyyTPrrI9LoWwQAtRtc+x8egxWcrZspNEPc9gktBYvjKdf1ihdrqlTOJe14LLli3zu+sjMr9P75R7T0RjVwhhzzeSsJe/k282EDpWsryJSkSZJt7l34Tz2bVrl8TWV7/m6e5RbUVbI9brJit6W460jZ13QxmN+iLQNHF/zesL695xZZ7m88MomH+zdIz67k5IPgy23OLPVfUqMfYB4fL4ru+haT+o1R7u/K5sjXzjG0SYxBwkN5/OE+X5gHBoepOUM5ncNOZD67nifQaTeF5+eQheD4FPOkD6qaLX8AKKovD7779z5513kpmZyciRIxk3blypXMvbnM3K4/2l+3lnyT7OpJfwmaiIZCfDqlc8EzgdebJgzUcxQFOngFHWadHC+LX8/d9sdpWZyw/yyLwtrNjt6WW0O1TGfPoPz3yzg/FzNvJ/Kw9zIiUbh1pCYlvt9tIAy+Rs4TzqL7nH1esuP58vKdmbRA9zzu1gmd9tR8nzoXUkPyDyKs8cgbAGrgZYJn9R3Puyn8zv+QOdeTw67sQlZvLmz3v4+M+DZFvLNoesTMVwUlNTiYiIQNM0PvjgAyb1CEP5Zcy5E+eM/iJq0/wW+F9z125fMcALdp+Xbniw+xv4abSshs2BcNN7rhWuLUcmgXscyxQoMe6xm3zb7OJCyDwDMcvEYNe75tzHWjPh8+vh9A4IrS+qXEsmSLhBMUrt812LSm2omqYxd+5cHnhA9LxjYmJo3Lj89opWVY0B76wkNUsMYbUQP0b0aISqwcB2dQjyuzSHm0/FcDRN+p7/8z7nlJ22hMDw3yE3VYRx8mVYwxvBY7HeGYuXmLHsAN9vOobVruJvNvDhqE5E15NF+J4TqUz6YktBj3IAf7OBuhGBfDamK/6Wcl7JkXwIjm8QF/75GmulHhPNksx4aVrVqDese0u8fEZ/uP4V6P6fshl3BSApI5ch763G5tAwGhTa1A+nW7PqhAWa6de6FibjpS3oLnR+l+lO3mazoWkaVapU4ZExw1F+HVe8ga8a5WqkYDDITjG4lriFDRZZPdbvUb4MPEjs2t3tdXKT6zWjn4hOuGPPFpfdBt+Xl52X4OoicnM+Aw/S6CZ+i/xv0096ZuFrDnnPpYiiKIwePZoOHUS04/bbbyc+vpj8jjIgOcPK95uOsfbAmSLNlvJZ+E8cZ7NsBV0YzmRYmf7bfj784wAPfrYRtaTdYHnm+HrYMotiDXyVppJLAxJ+q9IYancEFFm8mwNlIVjO2H0iFatdEuY04PBpVw+HqsF+RXbtuTaVEyk5rNx3uiyHeWlUvUpUKs9n4DUN5l4nmfeqXUrxUuNceveqrahgWSUmLjGTRRuPsfPY2RKPee3HPdgc8tlwqBrb4s7y4fIDvP3rXl79cXepj7Fss+udrmkjDs9OUoVJ3g8BkdLXveND0KCHPD92k6hkmQOg/dgyGPBF0mKIuOs1h9ysooe5XjMYYMQfUvObmSATQbWJG6yw8a/IxK6QxKF8VKvkUoTWcdbWa9LStgyYMWMGAwYMYPv27UyePJkvvviiTK6bT3qOjeGz1pNttWNQFO6+tgEP9r6qyHF7T6YXeU4DbA6NY8lZpGbnSZ+G8k5WkpSBhTeU+a2UsHs9GyOllJEtoNcLrrLKB7fArq8lQbN1+culGNi2Dgfj03GoGkZFoVNjV7lWzfAAXhgSzcd/HSYt20ZGjizaFKhcegwbpkOaWyjVYYX63WXOO2wSfuj0kO/GV4bEnslk9Ox/UDUNgwIv39aaXi2KNsg6lpxV5DlNA6tdZe2BM6U+zrLbyasqLHCqVVnT4a/n4Op7xL1THDnJop3cZrjrucAISVrp+qhkcTtZtmwZ999/PyNHjmTu3LnY7XZmzpzJyJEjeeCBB1i9enUpvjE36l0DD6yDG6fBfaugSaH2rrU7SqJNfoKRYpRe7N2eLpvxlQXH11Nk9xZSGx7cCtWixcPx/T3S0rKUufbaa5k1axZAkQZIZcGeE6nk2VWsdpUcm4PfdhSfi2B3qMU+DxAaYK4Yynw5Z2FmtIRl5veXZK7q0a7YrQeahH8a9IKGPV1PV20K170gMeGyjElfILd2qMvb97RnYt/mfDH+GupEeCbH3XBVMN9Vf4/fzffxdMCXmBToEVWNXlHVfTTiUiDmj0JPKLJYG7sZAquKl+6boZBbdOFa2Vh3MBGbQyXPrpJrU1myveg9RlW14iSeAFkANq9V+pVhZbeTTzsqtdb57FoAL9igxzOSfLdwsKtWEwBN9NLPw4oVK+jXzyVl++WXX7JgwQKWL3f1lJ87dy4bN26kU6cyEEKp1bbkfsubP5KyM9UmN7/uk+GGqcUfW1Fp1Bv+ftWVaKWYJYFw/48iAIImO/o/noJhP5T6cCIjpQJj7dq1xMfHU6tW2Ynx1K8ahEMVA242KsVO6GyrnbXOpjmFCbQYmf1A50uO2ZUpR1fLAi6/zHPrbJi4T9oW52aI4bemuo7X7CKDXMHo1Liqxw7eg1/Hw4GfMWoOhph/ZMhdt0GLNmU7wNImaoh46/JziyzBULO16Hikn5DnzuyWUE33//punGVAkxrBmI0KDlXD32ygZd3wIsfsPZVGUmbxYk51IgKYNqxdaQ+zDHfyQdU9MzTDG0pMvepVkkzX/wMwFHJJ+lcpchqbzcbKlSvJzpbYd2hoKGaz505n1apVHo/9/PwICQnxxru4dBw20eHON372XPjnA5jd2XPxU9Gp303CEk37S2nN6L+lw1hqnEsARNM8e1aXIp06daJmzZpYrVbatm1LcnIx/Q9KiToRgUy7ux2dG1dlQNs6vDCkaFOVcxlwm0PF31K+RSkLiGjquvEbLbKLNxhll2fPlnrswoTWLdMhlirpJyXxNv9vYMuGnx6Ar26WCoPKQsdxMOQL8cJE3w3jt0sORWa8q5pIU6XDYCXn2quq8Xj/KNo3jOCeaxsyvFvDIscEmI0lVlikZOYRUgZeujK5g9jsKm8uiWWNYQ5wlyTdaCq86i+lYGnH5cZgskBe/qpHKdLNzG6306tXLzZs2ECLFi3YtGkTVatWJSwszKMNaX4DnHy2bNlCVJSP+x+f2Fg0D8GWKYkrCwfLrqdUrutUBoxoKmEBUxnEdhtdJ18AB36FN0Ihzz0upYmc6bH1pS7oExYWxrZt24iKiuLMmTP8/fffDB06tFSv6U6XJpF0aVKynsM/h5NwD28EmI3k2MRQmAyGS86sL1OykmDp4+Kd8q8ii7pja+G1IAisJo1N8hPq8hNTFYM0laos7FpY6AlN6t5j/4QlE+GOBcX+2mWz70fp5NewF7QfU/rJyIoCre+VL4B1b8OK550J1M5FvGqTe06bEeW/augyGdShHoM6lFzOvHLvadxtvNmoYHNoKApl1gGzTHbyizYd48/dCSTnyLu1aiZx3zuskHJYvudrnEffI3HqG96ALpM8zvPHH3+wYcMGAPbt28fSpUv58MMPSUpKwmw2M3ToUGrWFAGNa66RLPDmzZvTqlWrsnibJWPLgW+GeJbPFaBJ3XhGgoQtvEnqUenB/e88ERhZMsG75z8f2cnw7R1una7cPu22bPjFLXlSVaWt7bInpUe9F6lVqxY33CC6CmW5k78Qlu2Mx+4Wkr+mWSRNawTTpEYw04e3LzZpKzE9l0MJ6SXXYJc1v02EuFWSTJqbKlUl2YnyP047Kt/zMqU+vsWdULsz3Law8rSDTomBlVMKzW+nsVVtcDZWVCpL0oq/VGJXwOJ7Ydd8WPoYbPnYu+c/H8c3OL2TeRQY+Hwy4+Vvkk9eltyDlj8jkuVXCEt3xhfM00CLgX5talM/IpCr64Xz9j3Fu+qPJ2cRl5hZYjXOxVImRv50em5B6QmAilK0gxnIarDhdTIp1r0J+1wa99u2beO+++7zOHzGjBm89957ALz//vs8//zzJCQkABQsBnJzy4GwSGqcS/0NKNJty2GF9+rD2zWl05O3SPjXFSKx50iDm7IkO+ncO4vE/a4EvBXPwLInJHt3TveiYkiXSf7ib9y4caxZs8ar574cWtcLw98s01AB1h5I5HhyNg/3aUa7hhFFjv9zdzy3f7CGBz/bxPg5m86ZtFdmpB31FLuxlyCGYg6E2u0gcQ/88QSc9FJNvq85tUVEn/IxmPFY0J7eAe83hBlNRarXWxzf4Lqv2LLhyErvnftCSD9RqEtoIfYtdiXgLRgMq16G9W/D7I5XjGBOq7phWEzyN8rOU/lzVwIpWXk8c0sr6lUNKnL8JysOMXzmekZ9soFpv+z1yhjKxMgPal+XQIuRQD8xOH4GrWgL2YCqMGgOLH1E3Fy5qdJC1rm7feyxx0hMTCQqKoo+fSRrPf9mPWLECO6//35aRbdmyANPMHjiVMY/JkkfR48e5eWXX8Zud8WIjh8/zsCBA6lXrx5Nmzblgw9KWXc5vJEkqChGCUsU179ZtUli0rInvXfdOvmJhvm1x4POebjXibgK6nSm5I+ZCj/cJ7kJ+37ydOW6awx4gUceeQQQoZz//rf8JATd0aUBY65rSlStUMwmQ0E2/ofLDxZ7/Mw/DxVk68eczuDfY6nFHlem9HzeKewUKpKstTtTpIVseCO49TNpPGPLEgOx6O6Lu052ioQFfn6wTKozLpg6nV2bFqOlaHvm/E5t6Sec4kBeonEfVztYX2gLNLlJcq1KwpYryYibP5bETIezc6gtSzY+VwDP3NKK2zrVo37VQAwK5NgcZFntfLWu6CbG7lD5Ys0RrHYVq03l1x0nScu+/MY/ZRLwa1Q9mO8e7cHmXQfp/zoYHDmeds4SDA9ullKrH9zi8JpaUHuZkiICC/Pnzyc0NJSBAwcSHx/PRx99xPDhUmb3+k+7SW7QD6td5azZyJOTzUyf9hovvfQS8+bNo3HjxgwYMIDly5fz22+u/sePPfYYHTt2pFu3UnIfmv2lxGTzTOkot3dRCe0zFeciwEuE1JLr7vpaEh3bjPTeuS8Eg0GaWswfALHLKVYY5fg6EctRFDAGgCNH/u+1L1io7YL4+GOXK/P555/36rkvB4NBYXj3RlxdP5xH58nOVlEgrISEnNAAM/Fnc9AAVdMIDSgHMftmA2DCLtGkX/o4nChURhneACbsgaR9nov7vIwipzonX/YVLXXVIdUajx8r3U6MF0qVRlI6u/MrOLMXDp+jt7o353e9rjK/Dv0uP5d1joN/KEzYDTNbyX2tMJpd2gjv/xGMJtdzpgC5H10B+FuMPNoviroRgcxYdgCrXcVkVAgLLDq/jQYFP7OBHKdqokFR8DNdvsZCmd0hqgb70WHX5OJftGXD2jfhlk+g+7MikagAnR8Bv2A2b97Mnj17AMmUb9q0KXv27CEvL4+AAFeHqh1HzxaEBYwGGDhyIv1u6MXIkSOJjY0lNjaWP//8s+D4r7/+mnfeeYdt27bx4osvsmTJEvz8SikxLawu9Hld4tSxyyH7LGiFVvxB1aD/DO9eN7IZXP+Sd895MRhNcPMM+KyreGeKoMmCxxQAV/WThUnb+yCiiVeHcfy49MYODAzk999/JzQ0lO7du3v1GiWxdOlSduzYwaRJk9i/fz/z5s1zJYc6Y9hNaoUzdPCH/Lgnk5ph/jw/OLrYc718W2ueXrCd5AwrI7o34qqa5aQDY5VG8NVN0oK0MFlnJG7cbrT0QYhxLvhuevfirnH6X5dCpi1bruXlz8klU7ONfCXslPyE/F2rO5EtoOvj3r1u/WtLvxvlufALFg/N/IFu7bHd0BwSvjGYRRcloAp0ebTydRYsiSOrYMN0bg1rwpam97IxNpUWdcJ4oFfRDpmKovD23e14afEu7A6Nybe09Ioccplq1yc+H0H1184SGQiJhaWNG98II51CC2nHQdNQQ+vy7rvv8uyzz2K327nmmmtYu3YthhKEMj784wCLnNrSAWYjCyd1p3qoP+np6WzZsoWYmBiee+45EhMT6dKlC+vWreOPP/7g1ltvxW63c9ttt7FoUelpqheQlQgfRUN2vtqRUQR0ujld9Yn74MQ/kn0eGAHdn3E1qimt8ax33nCvfVIWG95m59eSJHQ+anWA0Wu8fhP48ccfuf3223E45MarKAp///03PXr08Op13MnJyeHJJ58sEOQ5H3e1D2Hh1nR2xKUw889DhAdZePLmKGqEXdrfoky163PTYVpECcmliEu/96tSZpVyWPqWB1+kSMy8GyVrX3WI1++RQ9JvvryRfBg+jHL7Wxik6UyjXvLwxEYJR53aBtWi4JonSvd9JB0QL2JQTbjm8dLxfvz4AOyYc/7jrr4Xhn5Z/iTJvYmqigZEXqarRbfRT8IpdyyEf7+SVss1WkO/96R/ySVwofO7bH19AWFACRq/x9Zy4vhx8my2gmYio++7r0CK9NFHH2XatGklGniACX2a0bh6MKfO5nDj1bUKShRCQ0Pp3bs3vXv3ZtCgQaxevZqBAwdiNBrp378/S5Ys4aabbmLFihVefbslkpUo2ccFOFzuqz2L4IeRzoQaTcRk4lbB2I2lMxZNgzk9JNkRJFlm0gHvT8KMeCQ275YoZg6W+KUjjwL3bvw2Kcu57gWvXn7w4MFs27aNtWvX8t5773H48GFWrVrlFSOfnp5OTEwMbdu2xWazsXbtWhISEnj99dcLPFDujOrTgs7+TiEYVeVoqspb6+GbbRm89kYHJuRORXXmMRxLymLhpLLxOFwWfiHiii5IulPwcNkfXCJGPl8b41K4+2fY+qnEdNuPKZ8GHiBhR6HFjiqeDoAVU2DDu66/k9FfkkxvKaXM+OwU+LSLqIya/GR+3fWd96+TU/i+rshCXdUkBJfPnm8h+i5pOFYZUR0SVjrxj3id3Ft0710E/4uCZKcuSvxWuc/f9lWpDqlsjbx7PM4cJEl1mh1Ng0825fH4a82w2+18/vnnDB06tMDA//LLLwwcOPC8pzcYFG5uW+ecx1SvXp3bb7/d47l8JbzU1FTy8vKwWLwYNyuO1COShKe5CUbkq3+tm+aZnazZpPFNaZGXKUqD+W7Q1CNyQ/AP8+51GvaSHYQtW1zzvV6QSgp7jrTmLfhbaMW7fL1A69atad26NfHx8Uyd6h2lwbi4OHr06MGJEye4//772bFjB9u3uyokmjVrxsKFC4mKimLWrFm0iWrMDVvu9GjMZHPAN3vgaBr0eHMH9e47geKsLz6WnMX6Q4l0alQVs6kcK98pimfCmdEi8z3/s1xsDspFYg6QPuflnSJKforI/IbXh40feM5vRy4c+av0xpK0n4LyVXuu6FOUBi0GQcxSeW9GfxHMqdJIKg9+m+hZTeXNCoPyxrF14qXJTyJ2T0DVHC4DD/I3iV0BcaulP0speTe8etdQVY1tcSnsOp7qUeO3+0Qq037Zw8Fgt9iRokD7MdixcMcihYd+cZCbm4vdbmf48OEFhrdBgwYMGFC6CSWBgYEF8qfdunXzENYpFer38BSlMZjgwM/SijblsGc5jtECDXoWPYe3sARD1WYSMzOYRTTHrxTivHU6wvBlcO1/YPDnInlZrys0uh5ueE0WPQaztB7tPEk8DN6uKy5EaurlZ6Z/9NFHnDghdb9z584tMPD9+vXj6aefZtu2bbRr146AgACeeOIJbuhzo+diVzFiNsItzeRhfLqK4fiGgpc1DZ7/9l8mfL7J593ocm0ONsYkEXumkKjT/p8k471qcxHEMZhEBKd+D7nhmwOh//98M2hf0OI2z/+xyQ/+et7ZalrF48ZvCijdXW21Fs5GQYr8bxrfUDrXaTsKhn4F1z4lrYOj75Tqng7jJBaPQe5lQTWgxRAcqubzz3Op4BfiuaA5n7cpOwnm3wy/lp6Giddi8pqm8fSC7Ww5koKmwc1tavH0La04lpTFyI83kGtzYLCmsmHaMCJDA0g8tAWqt+SXb7/k1rsk63v69Ok8+eSTBQuEZs2a8c0339C2bQla8F5kw4YN9OnTh+zsbF5++WVeeMG77uIiJO6Hz3tJIl5YfVnd2rMBAwRGyoSMbAFNboBOD3s05LlsbDmSCayp0u0rX2IXZKcUWII2d2mSc1Y0ryNbiLvzmyEyrh7PeT1x8IMPPuCxxx7DYDCwaNEihgwZUuKxNpuNRx99lDlz5hRRUgRQ1aJ16uPHjy8ah4/fDnu/l7bJmialRQYj1GxH+v6VRExTcWjw3+4G2tx0Dx/Yhnv8ur/ZyOfjutKw2oV3LPRmTD7X5mDUxxtITM/FoWk80b8FgzrUFTf8d3e6PDRN+0uyZ9fHpLwq/ST4h0uC1pXEwSXw3V3yGa7aXBbvap4YusAakpBauwM07Qdt7/duQ57MM7B7oeTWtLpLQnFbP5F23Z0fLhvVy8Kkn5SwRK12LNqezPtL92MwKLwwJJo+0WXXT6LUOLwMjq6RRVTcKlj/DgRWFyPv7tkxmKVduj0Lj/ClYpReLhexmy/zfvIpWXn8cziJnDwHuTYHP249gUPV2HcqDYNz3H3tS+UHew7smk9MTAyP/FeM6bBhw3j88ceZOXMmERERjBkzhq1bt5aJgQdRyJsyRRSa3njjDdatW1e6F6wWBU8lwOSzcN3Lbv9cVRLybFmyy936mcR4UmK9d+0v+4pC1tLH4fPrJOO198vyVdoGXtOkSc+yJz3fU0AVcVkFRUoZZV6muLTXTfPuewceeOABhgwZgqqqjBgxgpyckoU5Fi9ezKxZs7BaraiqWuRLURSGDRvGsmXLaNiwIb169Sr4HBWQuE8Efta8Bj+NlnDEM6nw32QY/DnWoDo4NAjxN/DmV6u4+/kvWf9iX+pGBBTs+TQ0qgSVchjpHPx77CyJ6blk5zmw2lQ+X+38n8Stcrkm7Tlw4EfY8J4IsyiKVJVcaQYepJztmXR4Jg2a3uQKzzjyIOO4eDuqNIbVr8O3t0Fumneum5cFn7SD5U/Dz2NhyUPS3a/v23DtE6Vv4G250qBqxRTPOH1oHWjQnSzVjw+W7ceuauTZVV75YXfF39Hv/1k67615TcqFG/SE57Lg8SPi3fAPF89Ok5vgoZ3wfCZMTvNMLg6uUf7d9UEWE0a31WiQn4nULCvRdcNRNVBQeVD5suD1rz+eRrt2bYmLi6N+/foFN8bx48eTlJTEp59+SnBw2d4cHnzwQTp16kRubi69evVi6tSpWK1Wpk2bxrPPPktWVtG+wJeFosg/35Enu2r3/ts5yaICl3IQTmyQD5E3yMsWpSxbttyUE3Z47wZzIcwfIPK6G6bDh80h9Rhs/FBuCmfj5Bi3eDUohR5fPsHBwXz//feYTCaysrJ4/fXXi92RA5w5IxUQw4YNw263F/my2WwsWLCAvn37Ehsby6pVq6hdu7bnSY6uceWg2bJh2xyXtGdYXemjDvgFR8hCB8kvmX5vB6LrhdO4ejDThrUjLNB3Rj4y2A+H08OmAOGBZjJzbVIVY3bzMmmqxN9/e9g3Ay1PGAyi82H0k5/d5/fZGFg/HVJj4dBvsuD2Bqd3OSWErbJR2FsG1ULu/K8ZrHwB1kyFD5qSnpXL3L9j+PzvGDJybDg0zUMtQ/WSdKtPOfCz50J388euBU7dzvDfFHguG0Yslc0diMbAPb9C9auhThcJZZYSXjPy/hYj79zTjvpVAwjxN5FrczDk/TVsikli9gOdueeaRhicseakbLh3kYOMjEyu73cLS1aup2XLlgXnUnxUXhEREcHatWt5+umncTgcTJkyBX9/fyZPnswbb7zBmDFjvHvB2L/grWrwyxhXMo5STF2kprraOF4u5gApP1IMSGigaunE4Esixu3DrNrF6C9/Gta+DrM7yIJjwCynNKiTpP1eH4aiKLzyyisATJ06lenTp5/z+MjISIxGY7Ff7ucslpptPbOtz8ZIiVXMn7BjniTeFEP9yCA+HdOFrx/uRtemJTe5KQua1Ajh8X5R1AzzJ8BiJPZMJgPf+Zttpo5w1w/Qfqyn0IvRjzNpuaw/mEhyCa02Kz2bZsLb1USiW7XLoj4/30Zz6+XgyPOegl9EE0/1vZpl4wkFICcVNe0Eb2sTGKh9xeSchxj76Trm/B3DZ3/HMH7OJkL8TYzq0bjAuxtkMXL49EWKIpU36nZxKQ+CiCH9rzmc3Azb50pFQ3EelEbXwYSdMPYfqFG8LoY38GriXYdGEfS9uhaZVjs2h7hjZvxxkGa1QpnUoyo1GjSnj1TH4e9nptVtT0D3SUz8ei8bD5dystsFYrFYmDZtGs8880yR1xYuXMgnn3zCb7/95p3mAb9NLJRJ73DeKA1ihINqyIfH6Cf1695AUaQOvdUwaHUHjF7n3Xjg+TAW+rAn7ZO/gabKjfDMHmgx1GXk7Tmw6K5S0breu9elDd20aVFxCk3TLr+s0mGH3x9xLqqcd7b8XdaCQeJOXXSnPG9NB/vly1iWFgPa1qFFnVBybQ6sdpVcm4MZyw5A074c6Tqd+wO+5k7tM9YYe7G360fc9b+1TFm0kztnrOVYspe9YOUdTYNlj3t6oVS78/OvSKzWFCCPTf7Q/WnvXDeoGoxcAc0HSaz/zu+9c94LweTH7/RhCTeSRCTr6MKxs2IL7A6NI4mZ5OQ5GNC2DianlU/LsfPMN95tSFWmZCfDqpc8Xe22bJnLc3rAkodhdid4xQ+WPeVqx1uGePXuvnx3Al+ujfN4H/5mI/tOprHxvSHYz+xhyT3w2WATA8b8h5BWfcnOU8m1qcVq+fqSCRMmFKjp+fn5ERQkzQTGjx/PgAEDvLOrNxUSpcjPRFYQo5eVIBnmiiJJM94ivAHcPl+EGSIae++8F8J1L3s+zi+1AnnPkU4REfeSK9VRqMGPd1iyZAkgQjmDBxfV/R43bhw//fQTAHDkoHYAACAASURBVD17XmSFg8MuiUantkhCoT0Hj7pxo0XKBm3ZronvyIPt/3cpb6VMmPnnQdbuTyxonakgYbm/9iRwz8x17MsI5hh1+Y99MqOXBxbodGfn2Vn67ymfjt0nGApVKBv9nbtsTQy+Lcvl4Qn0ogBV3c5w949Se1+aIlqFMQeQ3OIBbMgC3YYFs0mMnwLUCgsgwGIky2rz0DvJyK2AvedtOTK/9/8k3seC+5Mri6ZA7Q9Nki63fAzH15f5UL1q5PedTPPoNmcxGXjtzjZM/mYHEbZTmHFgMcKw1mauqqoU3PLMRoXaVcpO5nDlngQmL9zO1+vjSkz6qFu3Lps2bWLy5Mns3LmTQ4cO8dRTTxXo5JeUbX1RDJojGciKQcqN7vhOmvO4l2BodvkA/fvF5V2rvND5YTHklhDnTsbsNHLOEh//cHmu23/kdVMAtHtAEvNKieIEcVRV5dNPPwXgu+++44477rjwE2aniDt+ZjTM7+/pqvevAqH1JAmnuNCMtfy6LnedSMXmNl/CA808dlNzXlq8q9AGxTNs4WcyXLJq38WiqhoLN8Tx34Xb+XN3fJlcs1gUBYbOl0W7wQwt75D57r6gzTf29lyJ61YC+va7laCAAIL8TNJdMf9zoUBkqB+KotCkeghtG1TB32zEYjLw0A1FvWjlmjN74d06Mr9XvkjBm1RMEFJH5nfUEMmid0dRfDK/vSqG06tFDRZvOY6qahgMCu/e0572DSPIyrXzOcOYok3HjoFMgtlEewCqBlmIrhfOI32jvDmUEtl6JIWXf9hFrk3ln8NJqKrG8O6Nij02OjqaN954o+Dx22+/DYjb3r2r3SVTqy3857TIIOavbJvfKtremsPZgU+Txi11ul7+9coDlkAYt00UofzC4LMuFEyS3FTZ3fiFQJ83xN2oOWRR4CMURSkinnRedsyVHAqHVW7g9bpJRn1AVbhtvhj6vEwRSPnrOTiyG3CqY7W7v1Tehze4uU1tDidk4FA1zEYD//dgVwIspnOGrmqE+dOjeXUGtju3SJW3+HbjUT5ecVhq+g8nERpgoXMTH5SEArQYDM86NQUURZLw/n5JPhuqXTxUmkM6+NUsvrd4RaNmeADfPdKdgwkZZFvtvPLDLvIcDjQNjiZJyEaSStsTcyaTYH8TtcIrmI79yhedfTg0Waw1ugHO7IJq0SLZa8uWudygp4gfpcTKxqVGG2jUu8yH61Uj37ZBFT4Z3ZkdR89ydb1wWtUVV9H4PlcxY5nKgzShoTmJtTnNyCaQhpFBZS7Zue9kGnaH3JRybSrbj54t0ciXGckH4d95MvGrt5Y4XcwfTlXAXPnQ7PoKOj0kqlkVDdUBSyZKeVXda2QiNLpedvB1u0piCsiNzuJWURHZzDfjdeOSci/cs80VI1SPhls/FdGLD1u4dvahdWHiAUg8A281goCI0ukb4CWGdqpPnSqBxCVmcW2zSGpXkffZv01tlu2Kx6Fq+BkNZDm7aPWJrsnUO9qU6Ri3x50l1ybXt9lV9p9K852RBzHuR9fAgV/l51Z3Sgjn2Dqw+IM17f/ZO+/4Gq//gb/vSm72EJEIEiu2qlmjSimK1uxA0aFbqy26dX6LVuevrZaq2Wq1FDVr1Sqq9giCEERCErKTmzue3x+fJDdXErIHz/v18pJ773nOPc+995zPOZ8pWe/++QQa3lu6+TDKidQMC5MWH+REdBL3tAhkXO9GtKtXjTSTBRcnPRargkaj4Z5c8fBarYaGAcXL2V7hOLmJEFes8n/TIVJ/YPFDMM3fPr9DusPY4+JpnxYrpbfL0/8pi1JPa9u4pheNazqmRB3avg5dQquTarJQt7ob4THJmK0KzWuVcurUQtC+fjVmbT6FoigY9FruaR5Q5D6MRiMpKSm88cYbTJkyBYOhBDm0k6Phh/Y3LruZHC1ZswbPL/57VRQHF8Ch+bJZObla4mjvmSqL3sj1UgoXJDNWOUZW3EiAOzk5kZmZydtvv817772HXn+D6WI1Q0oMpMbL3yA7+Lvegd+Gig0vt10+6QLs/hYaPVqi+yhPOjTwo8M1nv5v3N+M4Z1C0Ou0BHgZOXIhEXejngY1yn8R79k8gH9Px5FpsWHQa2lfv2KjEji/E37qkyvNaW5yzfnLh0UD1L7qhR5O3xDOfxHxmK0Ky/ZcoEVtb3o0C8DVWc+CZzux8WgMvm5OdG9ao6KHWjLM6eJol55gN6m6VoeWj8C0GmJqzc3Zv6XIWHBnKTRWQZRb7vqAXCqZazcB5UlooCcznujArpNxNKrpWazQpKlTpzJ27Fg+++wzAgMDGT++BJ7v0fsKJ9iU/OO4qwQp0VlFaBAVduJ5+2sGI7R+3P446j/Y+Jao8u/9UpJolAI2m40ff/yRzZs3A5LJLjutbX5Fj7RaLVOmTGH8+PF89NFHBAQEMHbs2ILfIOmimB7S4u3FhUD+ntXBMWQqF0r0Pr7/W5x2cofjVSU0Go1DJr5WwWXnP3Ej7mkRiKergeNRSXRoUI3GNSu4FO/ZzVlmt5uXmMQMzFnaUZuiEJdsv18fNyeGtrdrH7ccu8QvOyMJ8XPjxd6NcHUu3/IpxSbqP5jfU77L3AW1EiNhRhsxM+ZH7FER8hVIuX3C8Skmxv+0jzOxKXRrWoN3BrVApy2/U1tuGgV60iiw+JP/+eef58yZM3z22WccP17CGO4aLQuXo92thlTxqoq0GCFpHrPtkB0LSPxhSoZ5PUSrodFB/HF47nCx31ZRFJYsWcKRI0fYtGkT27Zty9Nm1KhReHvn74H8yiuvEBERwbfffsuJEyfybZPDri9E23JtqVXFBonn7KFS2X4WwOVUeOKbcFZu/RWAF154ocj3WFk4GZPMq7/sIyHVzOiudXm0a8XVee9Q348OFX2Cz6Z2J/nuLfmd5HPh3wxaPVouQyptRnapy94zV9BpNTjptfRslr929NSlZN5dcogMs42jFxJJN1t5f0jLch5tMflrvITF5cflw1kJj5zEiz4bja5s644UknIT8t/8dYKTl8RpZ8uxy2wKjeGeFlU3Z3GjRo1KpyOv2vDYVgmvyEiA9CuSEjR3SdbqTeG5I1W3BrN3HXjxlGTX82sMHgV878kX7RoLxQrx11bzKhpvvfWWg+Okr68vr7/+ek5GOn9/f3r27HndPgr9PeuMWZUFreJN7VJN7HDZQl/nBIMXoHjWInzhyxw9fIAn/jCTkLIPHx8ffvjhB4YMGVKs+6wMvLv4INEJopGYsyWCro1rUM//Fkxney0hd8GDv0PY72BKkZPfxf8c21TxGuutgn347cUunI9PpVGgJ+7G/M2XkXGpaLPu0Wy1ER5dgNCsjOiN5JRP1ruAkxekxeRqoMDTe6UGya8D5GSvc8676a8Ayk3IJ2VYsGaF3yiKQkpVjI0sK2q2hvtnyt8ZifCJv+OOMKSHOOaEr5Kc2J1frXoLgouPONtdD5/6EsOfECmPmxRcOKYwLFkiiUAGDhxIo0aNGDt2LLVq1SpRnwXSaTwcWyzZ+dwD4Zn94muwboJ8V27+kJlC/MGVjNpWj91/bgcUfOu25MCWldSuXbtsxlVOpJrsi5lWqyHVpM7vHEL7yj+QtLPft7JvZjV6mRdrxsGlg1KMqvmDFTfWYuLvacTf03jdNrcH+6DXaTEaJGT2/tZlNBfLgn7fwqyOkm48oBU8vl3qUBxZBCjiZHdhp5hnsn19LOmSzXPEqoocefkJ+Se712f/2SsoQDV3J3oWw+GtMhIbG1u6HRq9YNQ6SfdqNYHRF1KjYe/3Uq87ei+4+End92NLxSO317SqJ/TzQ6eHMf9Kvm0n9xIL+WxSU1P5+OOPOXjwICtWrLixA11xSL4oannAlhKLdvtU8Z7XaGTSJ1/EsvRJnEyZRGwQgVi99b10Gj6hygt4gBd6h/LB0iNoNdC8ljdNgyrO76ZSU6MF9P1WsiCiSNXFvT/IvLZZxPPePUCSIl3cK2WX2z1d0aMuFXzdnfn5uU78Ex5LkK8r7epVYNRDUclJaIVsxo4tyeUnpYFz2+HsFlDMdvOrRuOYnruCKDch37imF3+Ov4vLSSZq+7pi0Jd/KEFpEhgoKufly5fzv//9jzfeeKP0HKdC7pLqdMkXYcObcPQ3SYoD4qV7YLY9c1JcmOwu+88AfcUVMCk14o6J1sJqklCVhveWuMv169cDsHbtWo4cOVI2lQ0v7sFm0zB2Fcw9kM64HvP5oG81DFmZsH45rGHsGoUrWeuEVqulYa9HeXdIOeYWL0N6Ng/k9hBfktPN1KnmhraC/G2qBO2ekfrrKZfhl/sgajcOWWPWjINLWaleVz0jm/t2z1VI+FVpc/h8AnO3RuDmrOf9oS0rJAKjWOSutmhOE5Pq0d/smTlza+WzzXYeQdD7s/IeaR7K9VfjbjRQz9+9ygt4gL59+zJx4kQAJk2aRM+ePbl4sRRTd+oM4oV+dJFdwIPYhjKv8eQ8MBe+qise3lWdn/uKoL8aAYuGiB2zhLz55pssXLiQqVOnll3p4jqd2Rhh5bs9kG6BqX9dwmviCWp+Dr4fw/A/RMDrNBDkqWHO11PYPvkBbg+puNCa0qaauzMh1d1VAV8YDC5waq04beWOutDqIfGsY9s1L0qEhrn0UzuXJ1dSTLz/x2FiEjM4fTmFiQv3V/SQCk/Dvvb8FwZXCO0vxYCys1ZqtGJ6QSPJvF67Cq+ckzYVTNWXthWEVqvlk08+Yd26dXh7e7N582ZeeeWV0nsDiylvSlSds5QkvG1U3vYpl+Dfr0vv/SsCm82xBrViK9ijtQiMGjWKYcOG8dprr+V5bf/ZKwz7ZjuPTP+HsKhiltyN2gMrnuKqi9QBcHUx4h9Yi/RMK9HJcDUDXI3OzHy5L+aFg7iwfwOjnnu1wqotqlQC4sJh7UuOz7lUg2cPin3XAUV8Pap46tukdLODVTEhtRyKMR2YB181gNl3SVnr4nBsmeT2qHMndHgZ7npXIoAeXCIZSuveDY+shTZPQvNhUvSrPGsG3IAqEqRYebnnnnuYP38+999/P4sWLcLDw4P69eszbty4nAI3xcKUbI8tz+aJf6BmGwjpKqr8Pd/b4zO1elFv58ZmlT4MVSRtpFYLd7wEe76TnXG9ngV74heBkydPMn/+fIYPH06zZs1yns+02Hjl532kZ2VoGzd/D+tev7twwtecAX+OkWxmqTFkmDKZuVZecqvfgSYPvEGj9AS+ebQdfh5GvL29cXWtetnMVMqIpAuirbNmnc4NbhIu6hEID/wGvz0giaNyO+Aarvn9ZFcsrCJmujrV3Ghey5ujUYkoisLIss40GhcOK58VW3rCGVgyTNbQwpAcA0tHQuwxSL0sJhOdkzgFJ50Xe7tHTXj2kL2MbP17yu5eSoAq5EuBPn360KpVKw4cOMCsWbMA2LVrF8uWLSt+p67VpIjJ2b/FcavpUBHwICferm/DXZPgp74Q9S8EtRMBmc2ZzWLvM6dD6zHQ/7uq4ZzX+1PJfGc1QVCHUhnzfffdB8Dnn3/Oc889lxNCl55p4ezW09gU0DoZsbXoRmJSCn8uX0qPHj0ICAhg5aI50knqNQ6W2yaL802WzX3kUth4BvRa8G3RkwwrGN18iUg20LJRzRLfg8pNRu2OIiSSL4q2rucUxw3t4Pnym1vQS8LumgwWlXE2e3+QMqYAfb6E9s+V7/iLgVar4atRbTl8PgE3Z33Zp7VNvmivBJidryI3Nisc+knyW7QcIeHM2Sx/TOzwuUsFWzPhSrjd4S45WsKCa3Uo09soKaqQLwUMBgP//PMPy5YtIzw8nPfff5/ly5ezZMkSAgMD6dixY9FVsxoNPLxUHDy0enHGA0mN+mNnicH2CAL/FhDYWiq1OeeKS/7zCSmCAnBoAbR9GgKrSBGMmq1LpZt7772X8PDwnMcZGRl8/vnnBbY/t/Y7/D/TYDab0el06LQaMs0yyXubl8GlI1CjOcQcglN/OZS//TurUvK3T7bjp6AOZFpsgIba1dzyeSeVWx6DixRqOvu3hFxm/+Yjt4lfijldQrW8Q8C9hiTKyXa8s2SKgLdlpU5e+5IUNqoCGjudVlN+GRFr3SGCO/G8bKS6vO74+qqxkm7bminJul48Cc6ekt3u4l5HAQ+yDrsH2jdmilUqzlVyVCFfSri6ujJ8+HCsVisLFy7k5MmTOdXLHn30UebMmVP0TrU6qJ+VrCUhEmIOwv7ZYn/HJjv8xKyY8pXPgF8jOSHANWlwNVLx7ORq2RCUgsd6VeDzzz+nZcuWeHp6MmTIEFauXJmT1jYbRVG4lJjOzq2bOHMqPCf6xWq1YrVCDTeYPwh6hQJnNsK+WWImseafqrTv28uI3XOFE9FJDGxbizZ1bx7HOpVSxslV8l6AbCATzsDaV+yb8+i99rY/94WXzxVcwOj0enHiq99LtHoqkjL7qb0QuVXCEgOuya53fKndY95mEcG+7SOJXLrWVAoSEvv4P7LWplyCuz8Az8qvpdMUpcpW27ZtlT179pThcG4Ozp8/z/vvv09UVBRr14qhNjIyktq1axfP2SpqD8ztJkLfnJZ3h5lNu+ckaQNAxEZYeJ/8WBv0kRODJUO88/t9B62ucd6zWmQTAKIW1N1a+z+TycQnn3xCRkYGb731Fj/99BMH18zm3YZ78XfNKgP70FJYNDjfLFZ+0yA+TfIm+PlVjpSqGo1mr6IobQvbXp3fFcShheLfodWL/big+T30V2j+kPy9e7qE2gE0ewhOLJX5rTPCY1sg6Jqv3ZQi89utOoR0qxqmu7Lml4EQvkIORFo9DFshhaTyy0Ovd4Xu70HnieU+zIIo7PxWvevLgNq1azNr1izWrFnDbbdJqc3g4GC0Wi0ffPBB0TvcO1N+eKYksSPpC1DLhS2BzKydqX9zyTJncIEzm8RbX7HJJuHob3mvXTQYloyAP0bAL/cXfYxVHGdnZyZNmsRHH32Eq6srTz31FN9+PhV/9+zFUAMH5ud1bgQJoynoO1FRuRH/fCLCPTNZ8p9rCthg//uN+OOAqKINLuL0dWKZzGvFJhqmiPWO15kzYEZrMeEtvA82TSrb+6kqBHdFUtUiczhyWwFpaLUw4MdKJeCLgirky5iZM2cSGmqvi/7uu+862IkLhW99uxAxuIijTa/PwKeBY7vUS6LWA9j3ozjuZKbIApL949Ua7Pb9bDJTZZdvTpH2EeshowrllS4NbFYpIXn1DPxwB3xeGw79bPecVaxwZgMM+QV86oHBHdDKycm3YV7PZxWVwuLbwJ4ZTQM8+je0fxHcrskKen67XUBvzgrjMqc6njy1eqh5jbo+5oCUQM5MkbZ7ZpTZrVRaLJkSsXR+J3zdBL5qCBd229dFqwlOLJdshO6BcnLX6EXz2fh+aPFwxY6/BNxaOtkKoH379vz+++85J/pHHnmEhg0bFq2TO16GK6flRB7aH1o/Iar7Tq/AZC/IzCWQo3bL/0YvmfDZzjnZ2Mwi1CO3ARpJtlPjNjB6S+Y8ACeP/E+sVZG0eEiLE0FcUMawy2Ew9y6pG6A3ykKo2ODwz6Kmz8aUKOq8J/+V9KTR+2XxrHMn+o9kwzVt2jQmT55cZcvGqlQA980QIRN3XCJkgrvIv3s+ho+u0RCFr4KeH4HRJ2t+X6Pa17vAhV1SovnyUfEQr9XBLsw0Oqh2zeGgKpMUBVYz+IQU3ObkWtFUWs2yBmTb25MvIOfcLO1I7FH4e5LUnXDzlzXSZoHgO8v4JsoW1SZfDixfvpyBAwfSsmVLDhw4ULpJUDZ/ILv6bBr0gUfWiHr+t6Fwel0+TiRaidEFWVwMrtDmaXH0URTo+zUE3FZ6Y6wowlfLZ6DRiMPh6E32+87NT30l+xhSOCMnA5neKCd1U4Jje70rDP9TIhvm3Q2xYXx5oi4v/xoBwJQpU3j99Ws8eSsA1SZ/E7CgD5z+S/7WaOHOSXD3e+L49XNfuHQor6DXaEUzoNGKFs/gCne+CceXySm1//dVwmHshvwzTTQbGg20egz6T8+/3We1IDkq7/MaXVYxGZvj8151YPhKeW1BL4lkavUo3D+rUvkyqDb5SkhISEjpZznr9g4MXQSh90G39+GhP+R5vTMMXwGDFmSVScxNlu3Olisf/q4vpfDN6I2FE/DRB2DZ47DpXQn3qYysGy+LnDlNVJZnt9hfC18NX9WHb5s7ZtXTGiTphUYrG6XM5Lz9WtKkgNCKJyE+HFAY1zSK1o2kqta+ffvK9r5Ubh1GrBLTXOh94jDb7R153r2GlDbtlI+dWLGJ+Sm7oIo5TeZpvV6yOS2MgD+5Fv4YBbu/tfsBVCYUBTa+JeuYJSNX1FEWu74Sk9vsOx0jjTS6XGVj7f85kHgOfugAS0eJCVSxiR/T2c1leENlh6quL0eOHDmC1WotfVVu8wcLLk8Z3NVuz7fkzn2tFZW/NdvRRIGTq+DgfDEHZJMUBX+MlFC9DuMkHtecBnPuFBuf3ii55h/Mx5mvMFgtokrMtn0XF0XJu8t29iTnZK4oklMaRC3/21D7IujqJ+q5tDjJJth1EszvITUDctScWsfFwmoS+71iJTEDnl1tZt+JCwDcfffdJbsXFZVsss1ynQpImd1kEPz7VVZ2y1xhnYpN0mDnPGeFXZ9Dk4GOIXbR+2H5E7I2dP9QQvpiDsBvQ2SeH1si5r0urxZv/JZMmTsljdbJb37rjZBpdnwMEgq38U0Zf3K0mCNNSXKP7Z4Hv8awfoI9fM7hc8pGAxnXaPDyC6urAqgn+XKgSZMmaLVaIiIi6NmzJwcOHCAqKoqoqChSU/MJ1yhNPAIk9WK75x2dwwwukoM591bWmuWckps/HpE406sRsHYcTPWFpaPtGwZLBpzbVryxnVgBUzzhI3fYWASP38htsOv/JOWkxSTq9g/0ML2F427+vlmSTETvAu3H2jNTZSQ6Cuy0eBh/Ed5IglHroXYn8VFAIwuUZy0YvNCxbKTeCHe8xPlMX1rN0PDLYRtubm7MmTOHp5++OUqDqlQBgtrBmF3QeKAIq2z8m8npPzc2i+P8VhRY0Bti9stG/feh8LGfzPPsYjjmNIjYULyx/TMNJrvBZHc4/GvhrlEUyRW/+1sR0CmXYHpLmd8/3SvzHUTgP7BI8v07e8J9M8UPCeS67HVNscrjNxLhzRTo+5U9NwGI1q7u3aIR0ebeiCjQY7I42OqcoXZnSbNdBVFP8uVAaGgoa9asYdSoUWzevJnbb7dnnjMajUyfPp3HHnus7AbgVQvufAP2/QBosn7Y3SGovQir7BOt3hluG+l4bUKkY1iJYrHbCEH6Cu1f+LFkpsLWj8RGdny5/b13fgptxoB3cN5rov6DP58Up8Hmw2D7FDm5bNRLWEvkFhHaccdFhTdgFuz8EtZnTdxBC2QR3Pi2tG32kCwOKVlV+7R6SXSTnXtap4fHtsL6V+W1Xp+Bbz1xWNo3S4roNHsQmg5m/qoLnE14l2rVqrFjxw6HSAoVlXKhRgvo/KrEfFuRzXzTIeDkLh7j2c637jWzwsayUGx2Z9tsLKl2512Q9aHpkMKPJTlairmY0+DwwiyToAWWPy4x/vmZK8OWwIY3JJV3jVaSoVOxwub3xcco7piMNXKrFJxp86RoHw7Ok8346E3iWLt8DFw9De1fECe7bNLjZFxeYk7Du47ExG+bIhnxen8m/dTtIe+t0UK7ZyWxWJNBcqJ3D6hU9viioAr5cqJXr14cOnSIsWPH8s8/UiTBZDIRHx/P2LFjGTlyJHp9GX4drtUkW9OuL2Sy3/m6LAatx4jgcg+EEaulXTZXz0LDfrB/1jWq/lwE3yW2QpAIgCUjxI519/8kH/S1/PEInFyTf8Y4JR/bX/ZpIyOrOt3m9+ybDsUG0fvs19ms4hmfFg8bXpMFxmaBZaMl1//Oz2VTcW47OOeqEqVzklwEC/tLZMHDS8WjdvgKx7HUbGOvH5BFpkXG8vzzz6sCXqXiqNkahv0p5rbA1lmCLlOSYp39G/xbwsh1jmrz2DCo30c2uPnNR61BHHLbZmmmIrfDiqcADdw/E+p0dmyvKDC7S9bB4FqHtgIcvLPNgZZ0uHIKLu6x+wrpnCQlrS3XfLekiybv6G9Zm5QrcgDwqSuaQZtZbOe5tRo6J1jxtBxOvEPkc6h3t/zLTcPe8i83BpcqkS74eqhCvhzx9/fnt98cbdcajYa0tDSsVmvZCnmQvOsDfnR8rsdHovIz+oBfLiF17h8RrlqdTPZ6XSFineO1Blfo+pZ94fjtAbHnocjEq91JJh9Ikp6jiyQMMHtB0RtloiqKqNN96ko5yPUTRS3X4yPZoZtylYBVFOxhL4rY0a1mec7gAi1G5N0sKDax01lyOQiaEiQO1uAi93FihSyK6fGweBiMv1CojzQ7OkVbUHieikp5Ua+H/MtGa4T7f5AIm2qNwMXL/tq+H2H1i3JqdfUTlXfcMcf+9EbomOULYLWIN3+2I+pP98LrV2V9AKnadnSRHAxyhHuW349GA/1nyP9R/8Hf78lhotenoo7P7uPajYA53a5p0OjA2Qvq3SNhq7lP1TazrDu5w4WtJhHuWoPkl4/cIoeDhDOw+nmJQLpFuCWEfEqGma/XnSAmMYNRXepVqnziLi4upKenM3PmTMaOHVs07/urZySffa0OxSvJajHBzLaymwYJE+n3jfy96yvHMrbBd8LlQ5JgJ3uMNhuc3mBPrpMQSc5EtaTLKdunrrSb3Vk80a1ZjjhosjJ0Zcruul1WFa153SHhrAjzc9vEVn7baHuWPo3OnhfAZoHz/yI6SqSvxQ/BI39B59dg+1QZa99vRd12bInj/SsW0VD41MeSlshXO2D3RUAXC7slfahGo2HAgAEMGjSIadOmceTIEYcusisNqnHxFcfFq2l8sz4cq1XhuXtCCfa7SXI8xByUORXSDYyeRb8+6aL4qWRvqvt+I46zIKpqS5bjpdf5NQAAIABJREFUmUYjmrfVY2XO57ZNn9sO3sNlnmTm8h/KTIb0RHDzhbQr8F1LccTVAOikD41Grgu6Q6ropV+FeT2yMvvpxbz2xA7wayJ/28xgzbVBt5kl1h9FBHRGAvzYCZ45KHb0U2tFkPebLqf3v99xvH9rpmgBPGpKeViQNSezjP2gKhm3hJB/Z/Eh/ouIx2xVOBiZwKIXOlPDq3KoYF566SWmTJnCiy++yPLly+nUqROtW7dmwIAB1xf453fC/Hvsu+An/3M8iReG2DAR8NnC/NACu5D3qZdlr8+QVJtnN4uArd5U1OEpFwGLeOw2vl+0AdeeoP/9Rux5yVEyiXNU/hopnRuepQ5POAdrXxbb+dUI+/XmNHmvAT9CtVDJB2C9doLm8hewmeXfgblil+80PusE4A6n1snJXbkmpthm5uzpEwxf5sTO09njy4RDdo3LokWLrvsx+vv7M2zYsOu2USkbFEXhmdn/EZss393Bc1dZOaEbel0V16zsnyNCV6OT9NTPHi66oI9YLxv5bGH+3/d2Ie8dkrWZtspm+cAcOc3XuE3yZVizwkeXPy4+N/lldPz3C7j7Q7iwMyuULUtT5uIr/URmOeTG7Ifd30BgG8eCMLFhogV8fDusfFps+Mq1HuzXRLRoNKJ2H7YcUuMkYkbvLOth7hwX2ShWKThTrYGYE7V66DWtaJ9jFeeWEPInopMwW+XL12nhwpW0SiPkJ0+eTMuWLXn66afZuHEjGzduBGDQoEEMHDgQrVaLVqvl7rvvJiAgV5rL/6bbhbNGC0d+tcfQFhZrpmNKTO969r+7vSu73/M7ReCf3ymLRfoVMOQ6KWm0crqf2T5v0phsXKvbNwwarfTXqL+E7AFgE9Xc+ok4ZKDyrC0FNTQa2P9j4UJYtHpxRAK7ty1AYiSnEvTEJ1voUAtR49nM/H4UnlyZTmJGOkE1A3hjwiv41ayTc9mpU6eYMmUKqampNGjQgAkTJuDtbbfn63Q6unfvTrVquXwZVMoNs1UhNjmD7JxeKSYLqSYLXq5OFTuwkvLPJ3aBCGLmajKwaH2YkuwCHq19XgAMXiC28ISzEj56YVdWdE3SNVkyFYkbX9CLPEljsj/0ao1y2dGdIaS7RKREbs1qZ5X5vfENRyfehv3kpK3VS133ggrzXPuefo3kb7dchaCunMJBwGt0ucJfkfwhWr3c682SzbOQ3BJC/t7barJk93lsioKzQUfjQK8bX1SOPPzww9xxxx38+uuvxMTEMGvWLJYuXcrSpUtz2nh7ezNr1iyGDMnydPVtKKFhlnQRoNm276Kw6//I2f1qtHIaX9BbhHLvz2HIz9Ju3WuyyIC8n18T2RxotLJjjw+XeNvcaLTinGOzirNdRqJoBELuksxRbtXFJBB7VLLK3fOx2MqyFxJNlo39Q2fwCMoS2NljzedELhfJwtF+bM4zsbGxREREsHF1BO9/nUGmFca00TFizFjmzvqeeXvl9DHg/vv5cfbsfIX1ww8/zPr16xkxYgQeHh5F/5xVygwnvZY2dX05cj4RUKjn746nSz5ZDasavlknT5tZhFV+USc3Yve39r+1OkmgM/duSXbVYwqMzgqNm93VvoG2msQD/8IuQAO3jZJolpRox74NbhKxk5EIvz8oQtzgCk2GSsZMU5KY2DISRLC2fx52f22/XqMXO/oHBllDdM65hHw+J/Ls57u8lrf2BojH/eGFcp+KAr2/gL9eknF1nADViphK/CbilkhrqygKW45fJi7ZxN1Na+DrXsLEK2VMeHg4X3zxBcnJ4uRy/Phx9u6V2tJPPfUU7733Hi4GLfw1AY/YXeiaDoKeUwvOzV4Qy58Qb1ybRTYM2VWstHqo2RbG7JR2scdhZi5Vm94Iff5P8mtXayQhcVvez7VL18rOuckAybW9+GF7jezgrhKStvxxWQgMLuL0d+//ifPb1txV+nSIOl4j4Swpl8TppuUI2fnnnHQ00HgwNOoHrR4l02wmNTWVn3/+mVdffZX09IIz8hmNRj7//HOeeeaZ0s9GWMHcKmltMy021h+JxmpV6NUyEKPhJvCPSI2FZY/BlZMSw91mTNH7+K4VXDoof+uNIvysJvn79sftZanDV8OvA+0neL2LRJj4NpDiWD/1hVO5HNW0Bsm9Ub0xbJ0sc9+aKc/fMQ5qdczSymnkRO1TVxwAlz0mnvz2jgCbbP6bDhXzgs0MLYZLBrts857BHRreK4I8O8w1PxIi5bAR1E5y9yuKHDJu0rLZhZ3fN+fdX4NGo6FbkxoVPYxCExoaynfffZfzWFEUvvnmGyZMmMDMmTOZOXNmzmtBQUHMnt2TXsXx7r77f6KGjz8hqrzLYfZ0t7Fh9nbVG0soza4v5LElQ7xV2z4pj9uMgT3TRWgritjQmwyQ12xWx/e0WuDne8UrPjfze0ryCQc1m5K1oVdkARl3Sp43JcspwZwuJ4Lad8DDi1EUhXnz5jFu3DiSkuypakNDQwkICOCll16ibt26vPnmm8TFxeHv78+UKVNo0aIFKlUXJ72Wfq2CKnoYpYtbdRixsmR9DJwDP/URv5banbPs1sj8jcq1mQvtK6GhF3ZlPaFA/ElokBVO1v19ccCzWeS0PmKNrAkgz+UcFBWpXvnHI46RLFdPwS8DoEbLawaYfZ1NYthfvSwPL4eJXw2Ilq/1E3Dvl/bLMhIllDblspzsA7L69Q521HhoNDetgC8K6idQBdBoNLzwwgt07dqVp556ihMnTgCQkpJCVFQUvXv3xtfXN98QvNtvv50ZM2YQHJyPus8jEMaGife7NRO+bQqpNkADza8prdigD+ydIadng6tj9iePQBgXIXYx7xB7+liAhn0llO7MZjm13/slzOqYdyyW9KwCObk2BR61JOZebxTzQTbOHhLz/8/H4OLLL5ea8W5oKDExMTnaD63eCb2bN/V6PcHyr14nNNDutLR69eoCPmkVlZuIwNth4iWZ38lRML054CLCL3fqapBkUZcOyfzWaKVefTZB7eDlc+KjU60R6HP5O7R/XrRqiZGSa6PFMDj8k2Pfik0caq8tDuVWXQ4Gbv5SaTMb/6aSrGbvDxL22/malLqLBsumw5oJ4Svh5bPinKiSL7eEuv5mxWq1MmXKFD744APMZnOB7YxGI61bt85x4hs8eDAvvPBC3tju9AQI+128YxsPyqv+P7FCstSFdBOVeWHV24oiDnvOnjLRV7/oqI7TG0XFZ06xnyZ0zph6fsGHf5xgy87/HEu+5uLq1ascPXo057GHhwetBo/DVKczGo0Go0HL+L5NuK91rcKN9SbiVlHXqxSShEg4uVpyt9ft7viazSYZMS/ulcx0uePtb4QtKymNS1Zo8rzuEj6bmRWOp3OSENm9M+05LwxuMGqDVHxzr5ErVr4QTPGyF5Vy8pSiWkGF/pnfNBR2fqtC/iYgJSUl3xz4CQkJvPbaayxfvjzPa7169WLevHmOHvvlhaJIUgxzusS8KzY58e/6StRw5jSOJxh5eEMwB48ev2F3Li4ufPzxxzzwwAN4e3uzdF8MMzadwmyx4qTXseC5TtTyzScE6CZHFfIqFYLVIidtnRMkXxThX7e7JJk68afY3V184cXTEt5aVJaMkLK5VrMk1Xnx1C3nMQ+qkFfJQlEUDh06lGOjPnHiBG+88QZxcXFUr16dp556KsdjvHHjxtx///0V5oB2JiKCpd+9x4WzJ5mx6gBp6RnUr1+fyZMnExhYcLKfhg0bOmxWFEVh6/HLnIlN5a7G/tT1L8ZCchOgCnmVSoXVLJn20uIkXt+zmH4UVovkrU+/Ai1HShGuWxBVyKsUyMWLFxk5ciSbNm3K89rrr7/OlClTyn1M4eHhtGnThpSUlJznHnnkEaZPn66GrRUTVcirqNy8qN71NzH7z14h6mo6HRv4Uc2j6OGANWvWZN26dcyfP5/jx0UdHh4ezrJly5g6dSoPP/wwBkP5xhp/8MEHpKSk4OXlxdNPP02nTp0YMGBAuY5BRaWisdkUtofHkmqy0K2JPy5O6hKtUjLUX1AVY8nuc3y97gSgwVmv5ZexnYsV96/T6RzK26akpFCrVi0SExNp1apVKY64aPzvf/9j7NixN26oonITMuXPo2w4GiPFF7dHMP+ZTlU/Ra9KhaIK+SrGH3vOk2GWrHBaDew9e4V7mhejOM01uLu7s3LlSrZs2cLPP/9c4v4KQ3KGmYRUMzqthhreLjwwZDBPP/10uby3ikplZN3haEwWmd/RVzM4fyWNutWroE+JosBf4+HwzxIf/8BvaphbBaEK+SpGgxoenItLw2y1YVMU6lQrPa/SLl260KVLF956661S67MgzsWnMnL6DkwWGxqgQYAH/3u2U5m/r4pKZSbI15WzsSnYFEADfpU8O2eBHF8uIXPmVDi7RQT+wNkVPapbElXIVzFe698UZ72WiNgUHr4jmEaBxShBWQlITDOj1YoXvwJcSTFV7IBUVCoBXz7Shs9WHyM5w8yzPUPxqKp5+FMv2atS2sySjEelQlCFfBXD1VnPmwOaV/QwSkyTmp7Uq+5ORGwKNpvCmG71K3pIKioVjr+XkY+H3V7Rwyg5TYbAlg8g0yCpre8se+2gSv6oQl6lQtDrtMx4oj1hUYl4uzmVqtlBRUWlgnHzg7EnpJa8T73ix8SrlBhVyKtUGHqdlpZ1VGccFZWbEmd3CL6zokdxy1NhsRlFScKjoqJStVDnt4pK5aDcT/JJ6WZenL+HE9FJtKjtzVcj26gJH1RUbhIi41J5cf4eYpMy6HNbTSYNbF5haZJVVFQq4CQ/f1sEpy4loyhwPCqRxbvPlfcQVFRUyoiPVxzlcmIGNgX+DrvEv6fjK3pIKiq3NOUu5E1mGzabqPKsCjmJXVTKlpiEdLYev8zlxIyKHorKTYzJbENxeGytsLHcSkRcTmHr8cskpxdcclrl1qTc9eQjOoewKSyGlAwLPm5ODGlXu7yHUOlRFIXZWyLYevwSbetW49meDUuU2vJEdBLP/LgbrVaDoij8MKYD9WuoRV9USp9xfRoxbsFerDaF0AAPOjWsXtFDqnRkmK18ueY4xy4mcl/rWgxtX6dE/W04Es2Hy46g02hwddbz83Od8HJ1KqXRqlR1yl3IB3i7sOzlu4hLMVHdw1nNy5wPaw9Fs2D7GTLMVs7GpVLN3YnhnesWu78/914gPdeJatWBi7zYu1FpDPWGHItK5N/T8TQN8qJ9/Wrl8p4qFUfLOj6sntiNxDQzNbyMqj0+H6avD2f1wYtkWmxErgsnxM+NtvWKPzd+2n4WU5ZGVAF2nYqjd8uapTTa67PzZCwnopPp1NCP0CqamOtmp0I83gx6LYHeLhXx1lWCyLhUMrKEssls4/TllBtcIew4GcupmGS6NPKnXq4a6kG+rjjrtZgsNpwNWmr5upbJuK8lLCqRZ2fvxmy14aTXMmlgc3qUQp59lcqNi5Nedaa9DqcupZCZlZ9eURQi41JvKORtNoW/DkdzJSWT3i0D8ctVfbKWryunLidjsSooilJua+uq/VFMWxVGpsXG3K2nmfXkHTRQNYSVDvUYXQnp0SwAF4MOFycdRoOW+1rXuuE1y/ac581FB5ix6RSPz9xFZFxqzmsPdqhDv1Y1qeXryoDWtRjQ5sb9lQa7TsWRabVhy/K92Hj0Urm8r4pKZeaB9rUxGrS4OOkw6LR0aXRjk8YnK8P4eEUY328MZ+R3O0jNsOS8NrF/Ezo19KO2ryvP9Qwtt9wT649Ek2GW+W21KfynOllWStTtdiWkYYAHC57rxOHzCTQO9KSu/42rUK07HJ3jxKjTKvwXEU+wn2SR0+u0vHpfszIdc340DfLCWa8lw2zDaNDSKlhNfKOi0r1ZAIE+rpyJTaFNXV/8PY03vGbzsUs52r1Mi42Tl5Jz5pOXqxOfDGtdpmPOj9uDfTkQeZUMsw2dVkOTIK9yH4PKjVGFfCWllq9rkdTqrer4EBaVSIbZhkYDjSuBfeyOBn68NaA5G4/GcHuILw90KJmDkYrKzULjmp40rln4OdokyIs9EfGYrQo2RaF2tfIxuV2PkV3qotdpOHw+gd4tA9VNfCVFFfI3CY93q49Br+XYxST63x5E89reFT0kAO5pEcg9LVQ7vIpKSfjf0NuYsekkcckmRnQOoVolKEGr1WoYUQKHYJXyQRXyNwl6nZbH7qq8ldyupmYyd+tpLFaFUXfWpYaX6nipolJY3Ix6XunbpKKHUSBnY1NYuOMsXq5OPNq1Hm7OqmipLFT4N3EpUZK01PRxJfpqGt9tPIWbs46pD99OU9XGU6lJyTBzJjaVOtVcbxiX+9yc3ZyPT8OmKGw9fpmlL3dVwydvAU7GJLPv7BWa1vTkr8PRrNp/kSBfFz4b0Vrd6FVy4pNNXExIp2END4xOugLbpWSYGTPrX1JNFvRaLccuJvLN6HblOFKV61GhQj4+xcQj03dgstjQABabgtWmkGqy8MaiAyx/5a6KHJ7KdYhJSGf09zux2BRAYeYTBSfYsVhtnI1NzcmElphmJjHNTDWPilc5qpQdx6ISeXbObmyKhIppNBoyLTYiLqfwycpjfDai/J3FVArHgcirvLxgLxotuDvrWfBswQl2oq6mY1MUFAXMVhthFxLLebQq16NCj1IHz13FalPItNgwWezpbgHSTJbrXKlS0azcH0VyhplUk4U0k5Vfd0YW2Fav09K0lhdOOg0GnYYAbyM+bmpGrpudbScuk2G2kWmxYbbKBh7ApkihKpXKy5ytp0k3W0kzWUlMN7PpOuGvdaq5YtTr0Gk1OOu1dKjvV44jVbkRFXqSr1vdHWtWSUqDToOPmxNJ6WZsCjx/T2hFDk3lBvi4OWHQSYIdvU5DNffrC+2vR7Vl6Z4LWKw2BrathVarZkK72WkY4InRoCPDbMVZr8HdaCAt04qiwLM9G1b08FSug5+7M3qtBotNQYsG7+tsyl2c9Mx9piMr9l7Ay9Wp3PJwqBSOChfyUx9qxa87Iwn2c+PZHg25lJSBq7O+ULGjKhXHgDa1OHQugZ2n4mhR25vRXetdt72rs54RnUPKZ3AqlYLuTWtwNdXE32GXaVvXl2Edgzl3JY3qHs5qbvVKzou9G3HxajoRl1Po1SKQbk38r9ve39PIE90blNPoVIqCRlGUG7fKom3btsqePXvKcDgqKiqlhUaj2asoStvCtlfnt4pK1aGw81t1b1ZRUVFRUblJUYW8iko5sH79eoYNG0ZISAgajYb33nsvT5vMzEwmTpzInXfeiYuLi1rBTUWlCrF8+XJatGiB0WikadOmLFq0KE+bxMREHnvsMXx8fPDy8mLEiBHEx5dtzn9VyKuolANr167l0KFD9OjRA1fX/FOSpqWlMWvWLFxdXenUqVM5j1BFRaW4bN++nSFDhtC9e3fWrFlDv379GDZsGOvWrXNo9+CDD7J582ZmzZrF3Llz+e+//xg4cGCZjk21yauolAM2mw2tVvbUfn5+jB07Nt/TfHY8+TfffMMLL7xAUebntag2eRWV8qF3796YzWY2bdqU81zfvn1JSkpi+/btAOzcuZNOnTqxZcsWunbtCsDu3bvp0KED69evp2fPnkV6T9Umr6JSicgW8DeiMCr6P//8kzZt2uDm5oaPjw8dOnRgy5YtJR2iiopKMTCZTPz99988+OCDDs8//PDD7Ny5k8RESQ60Zs0aatSokSPgAdq3b0/dunVZs2ZNznOlPb9VIa+iUoU4ffo0Q4cO5e6772bFihX8/PPP9O/fnytXrlT00FRUbklOnz6N2WymcePGDs83adIEm81GeHg4AMePH8/TJrvd8ePHc/oq7fld4bnrVVRUCs/+/fvx8PBg2rRpOc/17du3AkekonJrc/XqVQC8vR0rf/r4+Di8fvXq1TxtsttFREQAZTO/1ZO8ikoVokWLFiQmJjJ69GjWrVtHampqRQ9JRUWllCiL+a0KeRWVKkSjRo1Yvnw5ERER9O3bFz8/P4YPH05sbGxFD01F5ZYk+8SebXvPJvsEn/26j49PnjbZ7bLblMX8VoW8ikoVo1+/fmzbto34+Hh+/PFHNmzYwAsvvFDRw1JRuSWpX78+BoMhx66ezfHjx9FqtYSGSh2Wxo0b52mT3S63rb6057cq5FVUqiheXl4MHz6cQYMGERYWVtHDUVG5JXF2dqZ79+78/vvvDs8vWrSIjh074uXlBcC9995LTExMTkgdwJ49e4iIiODee+/N029pzW/V8U5FpQyYP38+jz/+OKdPnyY4OJjIyEj+++8/QDLbhYWFsXjxYtzc3Bwm+Jo1a0hNTeXAgQMALF68GIB27doRHBzMjBkz2LlzJ3369KFmzZqcPHmS33//nVGjRpX/Taqo3KJcO78nTZpEt27deOmllxg4cCCrV69m9erVrF27Nueajh070qtXL0aNGsWnn36KVqvltddeo0uXLjkx8mUyvxVFKfS/Nm3aKCoqKjdmzpw5CqCcOXPG4fG1/4KDgx2uCw4OzrfdnDlzFEVRlB07dih9+/ZVAgMDFWdnZyUkJER59dVXlYyMjDxjAPYo6vxWUSl1rp3fiqIoS5cuVZo1a6Y4OTkpjRo1Un755Zc81129elV59NFHFS8vL8XDw0MZNmyYEhsbm/N6WcxvNeOdispNiprxTkXl5qWw87tIQl6j0cQCkSUZmIqKSrkRrChK9cI2Vue3ikqVolDzu0hCXkVFRUVFRaXqUCTHOz8/PyUkJKRYb2RTFGISMjBZrLg46TCZbTjptdTwMqJVS2pWKs7Hp5FqsgCg0UCInzvOhuIHYihAZGwqmRYrClDN3Rk/D+fSGWwZE59iIjbZJDcBeLkaCPR2qdhBZZFispCQmomzQYefuzPXTqO9e/fGFeUkX5L5bbbaiEnIwGqzYcya367OeqpXke/5VuLUpWQsVvlBazTQMMCjRGuw1aYQcTlFbMBATR8XPIyGUhpt2XLhShopGfa1roanEW83pwoelZCQmkmKyYK7sz7fMRV2fhdJyIeEhFBcm907iw/yd9glzFa75sCg09K9aQ0+GNqyWH1WFcxmc75JEArCx8cHnU5X7PdLSjczf1sEGWYbj3QOIaCIQmnoV9u4cCUNAFcnHR8+cBudQwstK/JwIjqJZ2bvJj3TCoC7s54Nb/Yodn/lydXUTB6dsZOkNDMGvZZZYzpQx8+toofFiegknv7xX7zNNpwNWga3rc24Po55sTUaTZFU7yWZ3w9/vR3X+FRyKwaNBi1P392QYZ1CitWnSv5cuJLGLzvO4m7UM6pLPdyMhV/GFUWh8/vrsWV9UU56Lb+/2IUaXsXfuK46EMWnK8NIN9sAaF7Li1lP3lHs/sqTkzFJPDv7Pyw2BX9PZ2Y/dQfulWCDsvbQRab+eZQMsw2jQcdbA5pxT4tAhzaFnd/lFkJ35nKqg4AH2f2HxySV1xAqhBUrVjBmzBguX75c6GtCQkJYsGABXbp0KdZ7vjDvP05fTsFmU/g7LIZlL9+FQV/4k/gjnUP4Yu1xdBoN3m5O3B7sU6xxZOPr5oTNZj85+HsZS9Tf9ThyIYH3/ziMyWxjQt/GdG1So0T9+bg5sfjFO4lOSMff04jRqfibr9LkZEwyIKcvk9nGwXNXK3Q80QnpXGv5yzDf/PP7eiSnm4lNNlGnmit6XemkJEnPtPDEzF0kpZvR6zQcOpfAd4+3L/T1Go2GAW2CWHswGjQikP09SzYfA7yM2You9DoNtXxdS9Tf9dhwJJqv/jqBq5OeD4a2pFGgZ4n6axjgyZ/j7yIu2URNH5dS+55KyuHzCWRkbZoyzFYOn0/II+QLS5GF/LSVYWw5fhknnYYMs5Xbgn15d1CLGy5+D95Rh89WH0ODTH4ngxYNGga3rV2sgVd2MjIymDhxIt988w0ARqMRN7dcJ0DFBhkJ9sdGb9BoSUpK4uzZs9x55514e3s7lCj19fVl2rRpDBw4EDJTIXIrS7Ye4+1Pf6Bfv3589NFHODk5ER6TnLPgppgsxKeYinSaH9i2Ns1qeRGTmEGbEF9cnUu2F6zuaeTDB27j2/XheLkaeGdQixL1dz0m/LyPhDQzAG8vPsTqid2KvDNPTk5m7NixrFq1Kt967kajkXHjxjFhwoRCl5AtbVqH+KDRgE6rwaDT0quYC0BubIrC+J/3cfxiIk56LSazlT63BfFCr9AblsC9r3UQq/ZfxKYoZFpEu6AA/W8PKvG4qiJHzifwwnzRivh7Gpn91B24FWEeXUkxcexiEnWru1PTxz53oxMyyLTaUACzVSEsqvAawmxe7d+UXi0CMVlstK3rW6jyxtejTd1qjOnegGV7zlPP353xfZuUqL+CuJqayQdLj5BpsQEmJi7cx5/ju5W4X1dnPXVKuMaVNt2a1GDl/igsVgW9VsNdTfyL3VeRHO8aNr1NCRr+ac4OA+RkdnuwD/83qu0Nd0FhUYlEXUmjvr87R6MSqenjSpu6vsUefHGx2RTmbI3g39NxdG3sz4hOISX+oW/evJnJkyeTnJwMQEREBJcvX8ZgMDB58mReeeUVR4GwcRJsnwKKFdBC++eg79dkZmbyzjvv8Omnn2K1WvN9r2ZNm+CRFkFSmpmwy/bvIiAggJCQECIup5CeKfZvg05DaIBnHntteVKjRg2mTJlCkyZlM/mzURSFLh+sx2K1EXtgHYknd7Fw+if07t6FjIwM3n//fS5evMjHH39MQEBAgf18+OGHvPPOOzd8v549ezJ//nwCA0suYItDZFwqW49fJtjPja6N8y4CRQ2hq9WwuVJ35OcOGjedBga3r3PDhVtRFHZHxJNqslDL15VjUUk0DfKkYUDJTlrFIT3Twv/9dYIzsak81KEO3ZsV/F2XFWPn/ceeCCkPajRomdi/Kf1aFW7Dc/FqOqO/34FNEXv3lyPb0CpLm5ZhtjLky60kpJnRaTW0DvHhy5GF/oq7z0ELAAAgAElEQVSrNOfiUxk5fQcmi6x5RoOWzW/fU8GjKjsOnbvKgcirtAr2oWWdvNrUws7vIm1fLDZbHpW7osCByKt8t+EkL/RudN3rmwZ50TRIUvzVq+Hh8JrVamXGjBmkpqYybtw4nJzsjgb//PMPc+bMwWw20759e5555pkS2az/+O88C7aLzTo8OpnqHs70blmz2P1FR0fTp08fTCaTw/MNGjTg119/pU2bNnkvMnqBzgAWq/xvlBKETk5OTJ06lUmTJpGRkZHTXFEU5s6dy1tvvcXRsGM5zzvr4IHb3fknvjpnzpwhJiYmz1v9WwmCovbv38/p06fR68tux6zRaHikcwjTf1rCmRVfANC/V3f69evH4cOHc8o5rlixgj59+mAw5H/CX7BgAQATJ07ktddey/P6li1beOaZZ9iwYQPNmjWjT58+BAUFMXHiRPz9i7/jvhabTSEu2YSnqwGjIe/vPdjPjZFd6pba+1mseee3VYGle85zWx0fejYvWFhqNBo61PfLeRxaAcI9m2krj7HhSDSZVoXjFxMJ8nUltIRq3aLiYTSg08jnp0FTpFP8hiPRpGdasWSZuH7bFZkj5I0GHXOf7siyPRdwM+oZ0u7m1ITmR21fV1rX9eVA5FVsisKjXetV9JBKhMVqIz7FRDV353wPyC3r5C/ci0qRVlxPFwNuznosVhtpmfZTpk2BvWevU9Q++gBYTRDUntxHSpvNxu+//87JkydZvXo1O3fuBODkyZM8++yzrFmzhtOnTzN37lxsNtm9zZ8/n59++ol+/fo5nL6rV6/OqFGjMBpvbF86EZPkYO84FZNM7yzfvxMnTrB06dICT9H5sW3bNkwmE25ubvy1aiXaM+vQKWZuG/wqzl4FOKy1fx7ObISzW6BmW7Ba4K/x0GEceNfBzc3NUb0PTJgwgREjRnB230b4cwxYTNT10RLQogMZD63k4MGDOZ9TZSEzM5Nu3bpx7tw5XnnlFWrUKLqNPDQ0lKFDh+arbfnrr7/yOIulbp+b87fFYmH58uWA5IJ2dnbm8uXL/PLLL9d9z6CgIMaPH0+1atXyvDZ48GA6duzIqFGj2LBhQ05fCxYs4PHHH8fNHAcZibToOoD7hg4rlpbIZLby7JzdnLqUgkGn5dtH29G4ZtkKKl9355zNRIbZ/vu3WBUORF7JV8hbbQpHLyTg5qyn/jUb94riREwSmTne4xoi41JLTcgnpmXy16Fo3Ix6ercILFB7+fK9jbkQn8a5+FR6hHrQNXIaRLtCpwlgvP5YArxd0Os0WGwKTnptHht3dU8jT97doFTupyqh0Wj4bHhrjl1MxNVJT11/93Ifg82msONkLGarQpfQ6kXydcrN5aSMHN8KbzcnZj91B9XcyyYSpcgZ7zZu3UF4TDJmi43XFx3AbLHhbNDxWNd6jM5nZ3V0xmiObf4V0EDg7dBpPCAe53PmzGH9+vU3HqRGw7PPPku9evWYNm0aly5dyrddixYteOWVV3B3v/6Xf/pSCvO2nSZ76R3TvSG1q7kSFhbGlClTHE7QRWHq1Km8VvNvOLdNVBzeIfDcYdDeQOswuytE7QabBVyrwUuRYLjBZmXvLNg+Vd5j8ALwqBiVcWEYOXIkP/30U4n66NOnD6NHj87RBNhsNpYvX87ChQvzba/Valm7di3e3t6EhYXh4uJC3759cXV1Zc2aNcRdioGIjZBxFUK6gYddgDk5OdGnTx8p/5iZBgv7y3ca2Boe+QtcvHPGsHbtWi5evMi8efMcCk9kM3jAfTw4bESBmiej0UiPHj1wcXH0mfjr0EWmrgjLiUhoV8+Xr0e3K9JnVpyMd6s2buNcfBpR8Wl8tuY4ZqsNZ72WqQ+3omNDxw2rzabw4vw9HI1KxGZTeOyu+pXidPX7v5F8u/4kiqLgbNDxy9jOpbKAZlpsPPT1duJTTGg10Dm0Oh892Or6F1lM8GUIpMbKOhDYBsbsuO4liqLw7fpwNh69RMva3rwxoFm+mhyV65B+FXZ9JebQDuPAzS//donnYUEvuHIKGg+Cob9cd72e9PtBtodL2dfQAA++f7x9sTbxX/11nN92RmJVxK9mVJe6PN2jYZH6KJOMd9emvTx9KZm/wy4RXN2Nns0CHG7WYrHw/nvv8dFHH3G9d/Dx8WHkyJEEBATw0EMP0bFjxxxP9AcffJCGDRvSt29fOnXqBMClS5eYPXs2KSkpOX2YzWZ+//13zp49W+h7uR79+/enZcuihfW1a9eOAfffj+ZDgzjVAehd4IUT4HUDldqHzmDNlL+d3OGpPeB3fdNHVcJisTB37lzOnDlT5GuTk5NZsGABCQkJ+b5uNBoZPXq0w4lbq9XSv39/OnToUHDHSx6BY3+AJQOcPWHcadlgXcuOz2DT29JO6wR3jINen+RpZrVamTdvHqd/eQUyEknIgHmHIDXzxvfYpEkTfv31V4ff3KawGD5Ycpikq7E4efjSObQ6n43Ix+xzHUqa1nbvmXj2nbnC7SG+tK2X97OJuJzC4zN35mjFXJ10bHqrZ5HGWFbsPRPP+fg0OodWp3oJvcezibicwhM/7MrZeDnrtWyZdAOb8JUI+K4lmFPlsUYH71pKZTwqBaAo8pnHnZDH3iEw9jjk5yT724OyDihWMLjBgB+h+UP5dmuzKXT+YF2OU7OTXsuScXcW6/f1/YaT/LzjDGargkGn4bG76vP4XfWL1EeZ2OSvpX4NjzwqOpPJRGRkJI899hg7duxAo4EeIeBtBDRaaHQfaOVtq1evzttvv01QkN0h5Z9//uHzzz9n0KBB3HNP3glUo0YN3njjjTzPT5o0icmTJ3Py5Mli349Op+OBBx5g6NChxe6Dao0gPlwEvcEV3LJstKlxkJkC3sHk8YKr3RnO75CTvJM7eAUX//0rIXq9njFjxhT7+gkTJjB58mTi4uIcnvfw8GD8+PE0b9686J1GbABLuv3xpcNQt1vedplp8r0AKBaJasgHnU7H448/Dk6LpW+bmZe6GPk4tj8JGflvcxVFYffu3Rw7doz27dszZ84chg0bBkCn+r5cWPoBp/dvp9btPXh5/fKi32MJaVO3Gm3q5rPxycLLxYAt1635VJIkInDjsReHGp72xF16rYZ6udXFiRdkXfO4xqThWUv8bywZ8npQ0bQxKsXAkgGxYfbDVkKkRDK55uPknZmS5fwMoIA5rcButVoN1T2ciU02oSji1OzpUryY+hGdQ9h1Oo4T0UmEBnry0B1lt+YX+SS/fee/fLX2OCeikxjYpjb3t6kFwIULF3jsscfYsGFDTvugoCB++uJNusX8n9jk+02Hhnnr5haJyO0QvQ/q9QT/piXrqyxIjoYNb4gA6fY+VG8MB+bDiqdEuDceBEN+dhT0mamiWjIli63eq1bFjf9WYfEwOL5M1KnOHvDi6fxVeimXYGY7SL8CTm4w5l/wCSm437R4WPksJJyBLq9D0yHXHUZqaipPPfUUCxcupE6dOkRGipfk6tWr6devX067Xbt2XV8zkQ/FOcn/9fc/fLr6GPHJJp68uwHt8jnB52b94Wi+WReOu1HP+0Nb0qAEdnlFUdh2IpZLiel0bxpQKbMinoxJZvaWU3gYDTzXM1Qykf01AXZLqCzdP4AurzpelHRRXndyE9Wxc/nbkm8pFAW+bSYqeBTwqgMvnMz/JB+9H+Z2B5sZfOrBEzuv+/1ExqXy6aowTBYb43o3olkt7xIN1WZT0GqLF/pUZur6Ye8vYPm+C2RabBgNWr54pA3nD21n9OjROSpVo9HI/fffz/Tp0/N1XCo2YX/A0pFgs8queMxOqFF2MdelxsfVREiAnO6f2gPVyzacrMK5uA92fAqeQXDXu5VvYbOYZGOVHAVtn7n+92HJhKTz4BF0Y1+JIpKYmMiIESNYtWoVdevWzYkAWLx4MQ888EBOu02bNtG9e/ci9V0cIX/7M98SFpWI1aZgNGhZPK5ruQnb7zeGs2jnOayKgouTjt9e6IKXa+XRDuRL2hX4LNBubtPq4e2MG/vhVHXCV8GBeeI03Gl85bvftHhZf2w2GZ/7daJeMlNlM+8dXPnu4zqUmbo+PCYpKxmBpPMOOxvNEw8+mBM+dunSpVINI3Jg83t2dYrNAidXVw0hr8/lVJWtxr+ZSbkMc+8SVZjOGeKOw/AVFT0qR/TOeU9cBbZ1At+i2cswpUBKtJwOrrNwfPjhh6xatQonJye+/PLLnOdzh5Dm97isOBeXijVLB6/VaIhJSC8XIW+1Kfy26xzpWV79ei0cjUqkU8P/Z++6w5sq3+i5Wd2lUPYehbL33ntPGeJAUBBRUBy4cSsq7p+KDBUFlI2IMmXvXcousy20jFK66Mq6vz9Owk3SpFk3bVDO8+SBNMnNTXK/713nPa/ncspFAqUagEUkptSwLPlvxtUDwPJR3IvPrwV0uUC3d4r7rKwRHAn0/Ni152pCgFJuEkZzUoH8TNb7/Xz2ittGfnirKoi7lglAgEohoEfTGmjbqhl27N4PALhwLs43Rv7qQRqLuxCBck3kfx9fYORSYMkwQJsFdPuAHuO/Galx0kZnyAeu7i/e8ylqJB0Gfu3BGn7JmsCE/dxI7ODKlSsA2EGyceNGbNy4EQDJiuXKlUNoaCjy8/OxaNEiq04CQRAwYMAA9OvnZfnLBgObVcKqQzynkiEa1C4fhgs3srAnLgW1yoWiY7RvHPi1MUlWbXv5eiOqRRb/jACnCAgDBs0F1k6mM/fAIr/f9L1G8mGp3q3LARK2A/AzI+9LnFgC/Pk4AAGI6gs8uNKvf3O3jXzvxhVRsVQw4lOy0bpmJMLFTFw+eRAAUDoYqHruB6BjJ/cOKorA5W2si9TsaT/yybwCqAIBLSVLEVoBqN3X3dMvHlTtALziuna9U2x/D9j1MQV0HloDVHZdu9qnEEV6uGUaMIJXqBjZRA8p7jMrWmx5A9CaNNvTLgOnVwBNx9p96qOPPoqVK1ciPz8fs2bNKvC4uV109uzZBR77/vvvsXz5cu+IojaY0rsOWtYshfQcHTpHl8W19FxMmHcAOr0BapUSU/vUwbBWVd06plZvxKFLqQgLVDkU97huo33fqkYkKvlQA11WNH2MNzlgNAArHybju1QUMOYf/+HoGA1sTavejV0CgoJZygb22ej/Wmx4nuQ+ALi4Cbh+jO3hXiJXq8fHa07hTFIm+jWtiMc71/RaiRXwkF3fsHIEGpoIB8tnzURiOr2645OACrc2F/ZSa2RcAc6v5wV9ZQ//VrUT8Mjagp5RzZ5AkGmDEA1Ar0+B67HA7k/JYO/2Hlms/gBtNpCXwd51uT28lDP8zIZ8IPsGsOoR4DnPOwpkgzYbmN8FuHkCCCxJ7/bKXv42TWTaAF2BQQ/E/QkYdEC9YUzLe4PMZKbdyzZi2t4VaEK5CZpZuxrHfIRBgwYhJiYGO3futP8EUZSuoasHgZOLAYMOP8cKOJosYsuWLbIaeUEQrPrh18fehlEUYRABg86Af07ecNnIn7+eheMJaVh+KBE3M/JgFIHR7apiUo86BZ7bt0lFLD2QCECEwQhM7FEbOL8BOPojUL4p0PFVU2rcD5CbzoAkxAelhNMrWe826oHU88DGF4BRy+V/H3eRngD81B7IucUOojGbgPjtLJdGDyq688jPImE2sCRQZ4D3+2vqBWYjyjVy/ViaEMDcZCMa2XrnKYzGu4TAHzafx/YzN6HVG7Fg12XULh+GTjJkzrxqoVu7di0efeEjAMAjjYAKJTRsGTm/AYjqU/iXlnEVmNWIBCiDhfjM5S0UjrAlSgSWAJ45CSTsYro7tAJFJrRZjBZvngDGbvHm48iDS1uBxYO5wdfozkhbTjKHLse65ldIy0eR4vgitq0YtEBOCtnEI5cW/XksG8EWNoDn8MQuzzeCuL9Ze1QogYgawJMHALULg376fcPS0u0LQN0hQN2hhT69UaNGaNTIhluSncKUf8pJoFpnoO9XQMxZIICOg0IQ8UyyZx/LHdStGA4z+TdAJSAsUIWTV9LRsErhrOLYxDRMXXDYNLBGCtGXH0i0a+Srlg7Bsmc74kxyBqLKhaF87llg2XBe3xfWs/5pR5+gyHFwFg0vALR9Aej1ibzH12UDZmUR0UBeiz9gx/vAnes0aqnngKQDQOc3ivYc9FpgbksgM4n3m44DBnzn+fF2fQLseI/7ae3+wMhlru0VwxcDi4ewLa/zdKB0wevZKW6cpAhP9g1+jlbP4M71ZGj1DCSMoohrabmFH8NFeMUQ+fLLL6HVatGzU2vMmTaMhjj1HLBsJGtUheHSP/RWDTbqckqN44g8IAyo0x8o2wBIuyj93aAFko9481Hkw7opXKj6PCBhJ2VrAXpsJxYDB75jz7ynKN8MqNWbpQtVIND3G77HnJbA/K7ArXOyfAy3ISitF4hQDFOdDHogbg2/f102a4fZhZRJDHreHGHLG2yF1N4B0uOBi87VGQFQ/GjKaeBtLdslPXHytr8P3DoDQAQSdwPz2jCqVSgp3lNEUW3DKhH4YGQTtK9dGoKgwMFLqZjy6yGsOXK10NdtOn4NeTqjlYEXBBQ6tzwyLAAdo8tyYuK1o9IDuhwqDhY3RJEG3qDlbf9XdMYA6ikcngsc/QnQeaaYCQCoP5I8DnUwf+fuHwExvzAgWjqcbP7igEKFuwRDQeB6L2qknAaykqX1Hbug8Ofrtdx3HWHHe9yndTnAub+ZrXAFlVsDL18D3sr13NFZM4EZQtEIHPsF+LkjpieNwgjFBgQHKBGoVqKrl2OyzfBqJ9bpWB9/8/1PEVK/LDCvtaTsdOwXYGDBGuNdlKmPux6rUgMERADhFYH+37mWYi1Tn2kTfR43vKJMGRUGlUWLlShK9/+aCJxcQu98z6fAlDhA40HNUaFgKjw9gZuAQgV8UdH0vQvAb/2o3lbUaPwoo/nEXUB4FaDnjMKfbzTyu5DTWCmUQFhFbgQQGXUHOhjwcHgusO5Z7lsDZgPNHy/4nJCyoB9s5GK0p4gnN8yFaX2utEGJBt6MOv7eA34A1BeBv96GVuuCpJ6X6BRdFnlaA44lpN2dWbHsQOJdjQx7qFMhDIFqBfJ0RqiVAiKCNahcKhjTh7ooXFS9KwCTMVEF+k/dV6GS2uUAQKHmb/ZLFxohAIhdCDy+3bPjB4QCk47RqQwtz5T9usk0RLfiAHE8MPoPbz+F++jyDmWg0y+zfNJ8fOHPN5pKVXJmMcMrS+tDUAKRDiJoUQTWPwcc+oHO0iPrgGodCz4voIRUWxfBINLXMKfn9RaOoGgE9HlQAHghcBFaDXkNjauWlE1cyqtIPjiYRmrq1Km4nm1xKEEBlHQyHatyG2Dwj6zBt5gIvBAPTIohSc0VaEKAp2KAHh/RMRgy37MPITeG/EzjICiBJmOBKu3499MrpAg/LwNIOeX5ewgCBVmCSzE1bma6QmQZpDigDuTG9kY28PzlwjsILm4GPg4HPgwCNr8p3zkIAjBuGxmvNXoA47bbr6PrcoH1zwJGU0T29yTW8G0x5CegfBM6Cu1edP3a9BQHZwEfBgIzQtl/HFIaUAbCqkVLoQbqj0BwGdbFXZ3/4C2qRAbDaNpg1UoBtZwMBxncvDLGda6JJlUj8GS3KKx5qQt+eKK162S6UrWAiYeA7h8wG9J2qrcfwXsIAvDAbzQcSg3Q92vOMchJBW4cpyE2Zx28ieYVSn5+TQiNqjlqNuokqdaiRnhFcn/eyKY+iYNuEQDAge+5tj8KAWJ/k+8cQkrTYFftxDKYo7bc67FAzM+mckcWsHqc/eeNXs0WuJCyXOu+dOJFEfj7GeADDTCzHNB6Cmv5CuuWS2VoaXSpV05W9UivtOv37duH/v37Iz09HYMHD8af37wEbH6NrO+BP1A8JPc2EFzavtrQvQi9lmnT3NtAsyd48duDBaECAElpV/ZxoWpCgamXWWs08xc8ZecajcDPHclJEEWg8Rhg0A+eHauo8HlFpqrMaDYBGDKv6N5fmwN8EsHfAqDhfOOO68Q6XyA3Hfi8nBQlqoKAaTeA/HRGiH+OpzM35Cegdj9kZ2djwIAB2LGD5aCXX34ZH374oVU/vbfa9bZYfywZS/YnoGbZEEzrXx8qpYA8ncH/BWvcQc5t4MhcZhNbTLRvzO5Gkybny2hgNi3HVIYLrww8ewE48DUNTrMngJrdPTuf3HRgVgMSzkQDy3MtPJeI9jnys4CZpa2zHUPmA83GFd05JB/hfmvOKkdUZ+BRnLiyD1jQSzqnsg2BJ/ayC+fsn8D2d4CgSJIsXdR+KZIBNQCwefPmuxrzJ06ckHTETy4FVj7CjalkTUbpRZEO8TWWDKdxNurovDx30bW0e85tOkDZN4BObwIZicDqsfT81cFcCA1HeXZOei1wYQM3pBrd/bpnEwAwsywzEGaoAtlLXr4IdQ/2fkH5YUEAen8OtHm28OcbjeSBBEXa18D2Ftm3gC8rWW+OqiCWZhxIQRsMBnz88cd45513YDQa8fzzz+Orr766+7jcRt4SP2w+h193ceNsXasUvn60pcfynH4DowH4rh6QkcDoqkILYHzByYJ2kXoB2Pomo+6eHwOHZpH4aV7fE/Z7LtyVm05CckR1oKJ7Q4qKHHkZwGdlC5Y0Xs9wjbQqB0SR0fuJxSwHjl4N1HIySEivZdYkvHLhWQpPcXk7sHiQNZEyKBJ4fAc5Zh7A1fXtdXjdtWtXNG3KcYutWrXC2bNnuVhWPWpqIRK5OR792du38g9c2mSql5qGlaS6SHQLLgUMngs89CeJGwk7JWa8Lof3PYVKA9QdDNTs4b6Bv3oAOPAtB7QUFQbNtfmDTY2qKND+JeDV28Arqc4NvEEPLOgBzG4KfFkZOLdO/vMJKQ20e+nu8CYAvM7+dFz7VCqVmD59Or744gsAwJEjRUM+TU7LwYJdUmR06OJtxCamFcl7+xTZN6nHYdDyeryyV6otO0NkFLtJRvzOUtXlbRadL4J3xOCgCM5AcNfAiyLb8Q5+X3RlvMASDGJs4er3KAcEARj2K/DyDa5xZwY+5zbwXV1gTguu75un5T+nap2Aal2sCcm5t4GNL8n/Xjbw2sirVCrs3r0btWrVQl5eHrZu3cq2uAI/qusZA79GxVasx0Fg7aykh/Oz6ww0ydsKgCqY94sa5zcAv3YH/nkF+LEtkHQI2DmDAxv2fwO4keVxC/WGAqNWsd6sDKCoUaXWFI5JveCb97SHgFDXNPUTdpKpr8uh4TW3UMmNnjOAcTusZZBtJVJTzrKT4pta7KkG0Lx5c9+cjwPcztZa0QREcCb2PY/gMuRfCAo6W2Xqe04cqz/C1D9t+l6q2iF++Rq7PwWWPwhsmsbRq2nxJJv+2gM4u8Z379v1bQ7qUWi4V3Z5i9HxzdNS+1tRIKikayTu2AUSaz8vA9j5gfznolCSQ9D/W+u+etv1fWkL8G00MKsxlTNlgCx9TiEhIejduzd++MFUC9YE8yI/vQKACASXBVo+JcdbWePSFhqmWr2BikW00Y1eDez8EMhNBdpPAwLDPTtOVG/g4bVA/DYyiWu4N3xEFhxfZN1nv+0dIGEH/5Z0kOxeB7OVvUb9YUCtm6zhhVUAtr4N7PscgAA0nwD0/59v3tcTaEKtHR6NF2WnS1uBP5+Q6uu2UUbV9hyYc+B/3KCG/mL9+JIhZFxDBFaN4ZjiIkbdCuGoFhmC+FusLzasXAKNnPTNuw1RZMkv8wrQYFTRSEErVUyr7/qIzmeXtzw/VoeXmV5POc0oPDJKttN0GbG/SjVghZrX3ZV9bFu+ut+7EoIzdHkLaPUMf8egUsDvg4H4rbzu+38PNH/CN+/rCTShNMIG0LkL8HBPB4Aj84Ctb7GUO3KZ9aRUQWBXwtk/aLuCS1P/wgxtDvvvzb/Zor7AKylel19la2a+c8dGtGHkUl5IBh1TFXLXiU8tZ91Fn0/P6/FdRWPoA8M9F+U4v4Hp/ehB7D6o0dX+DPOiQqXWvODMdUN9vnUJ4dox3xl5gByNgDBeI7s/lhTiDs8mq9pfFAwrt+YI4AP/A0LKMRXoCYwGCiWZF/GSocBr6QXbCPt+CfSYwb/bRpJZ13A3K6bPBeZ3AuoUrUiMSqnAwqfbIzYxDeFBatSp4MWm6AibX2Oa2aAFds0Anj3nG4U5W0RUBQbNcf91RgOdkvwMoOFoRpGecmzkQsVWzI4Z8rm2Mq9KuiSCkg6ILwd8mdnq12MZzJj3ls2v+peRb/IYB+2cX0dly+4feXac25eA9VO5LrNvAMtHApNtuqiUamDMRnb4qAJtRo5nsQxsRm4qsLAPBdW8mH4pi5H//fffsXDhQgBAyZKmvmRBkNrH7CHpEFuXRJFz5qu0de9NTyyWLhp9PnBxY9FF855g39fA1un8Ebe9BTxzSn5NaoOOqeWAcKBSK+fPbz2FRJDLW03RRh0gaT+9bUFBWdiigKBk1Gr+PRVKRlL+hF6f8uYNzLVe2/v2tAIcLeoOr9CpNROb0i6zH7iIoVYp0LKwWfOnV/J6Dy1PUmnJ6u69wanlkjMkGplZqjPA4/P1OVaPA878wXPd8xkw5Yz3ksq2yM8CEvcwQCgd7fz5A39gp1NqHND2ebbfbZ1Og69QsUZcFAgIlxx4gP3p/gSVRh7tgdxUa6c8O8Xxc+2REEPKkmR7bq3U+ZO4m91cbaZ4fFpe1+QzMjIwdqw0fGP48OHOX2Q0UtLv2lHgegywqE/hymP2UK2TNLJVFUAmrD/DnDoz5PPzJ+yQ9/hGA+vrS4YCv3QFtkx3/hqFAuj4GlNr5ZuSmf/4TrLNJ+wvusE3CgXw4Cpe5EGRpl5keee2+wXUQUzFq4N5azbe/Y6TLtNZJjI7QaKBkYM/IT2RpYRbZ+l0LnNhT7BF5baSkJRRbxLP8mOcWWXSwchl54jc/ey56cD3DSizPKc5nSBn0ITQMW33EgWq2j1PY9bnS+Dp469OFkMAACAASURBVEBYeXnP0RFK1gB6fkrjXqJa8chdFwUqNKciqSaUvJpu77v3ekEARq3knBYzl8Oo91q63OtIvkSJEhg/fjzmzGGKa/fu3eje3U5PaNZ1ChQERgCNHqZXaoZZRELpRtqvzVRmARJ3sWYX1dvLT+JjVGrLTU+fB8DIPkk5cSsOuBYjRT/7vwZ6fFj4a0SRTsHlbQBEpq0GzpK/TefkMkpIhldmVGdPWyCqD9mw/3b0/5b91xCBco3ZWnNkLq+HDi+7pgDY4VUalYxE1lrrPQHAxVYvX+HmKXJwIqNZizZHNKKR5+kuBv9IeeDbFymE40xcq7hRtiHXn1EHQABKuDepzykubADy0qQWrN2fAA1GFv4aXS4wuxlJZUYDZyq0mOCcbe4ORJHllNiFLP8NnG2/pbjtc7z9m6FQUowr+QhLFaVqAbGLKJkb1Yca9c7K1goFf6cf29FWhJShzoIXcMvIZ+bqsOF4MnrULw+1SkoCzJw5866RP3v2bEEjr8ul95lzi2miS5tJzDu3lg5Lrd7uE9gUCqD9i7z5A0SRiykwwn6fZd+vyOS+cRJo/Yz8PeEhZSyU7wSmSZ3hzg2OSjTk8/6RuTRCckpRpl4wcSdy6YisGA084UW74L0OQQDKN+b/b54Gfh9AB1cVxAjQkojjCIHhwNMnKH0aVgHYL1PrXM4tIO4vdnq4w6FJu0xtfV0usxUdXmHXSdplZhraetCNoAn2vjwiJ4wGMsNDy9sXTXr4b3ap5KQCXd9l25ucKFFFWt8KNQcmOUPCLu5JWlNAtWuG/EI6cX9x7LUum1LbwZGuXcP/ViiUUgb09Crg76dM2vh/sdOg8SPOjxFZG3jxCq+3iGpeS3+7ZeSvpefi0zWnsebIVcx6nB9Ep9Ohffv2AChz27u3nYg69Tw9UKOOt4sbgdezOKoQIucT38swGoDf+jM1KZhaJWzZ8upAoPdnjo9xfgMXTPXOnpHdQsowDbZpGh2NoS6Qw8za92YjH1SqYEuHt8i8KvV+iwYg7ZK8x/c1Us8zNVqyJn8XOQmk12Ok71ufy6geYC1Pl8No0N776XKZFYqoLq9wR8YVYMVD7ITp84Xrr0vcYzpPIzf7s6uBCQfI9Qgp4xo/xJ+Rm0YnJvMqU7ET9jFKs0RIGWCoA2ltUeQsj+TDzDpW96AWXrUD0O0DCuyUrsuI2RnCK0m1cEHpmw6F9HiJLGbIKz7ZXU9xZR+Z7pXbArV6ynzsvQW1UBo/Qs0CpRoIdTCAJjedwjyR0bLM9nDLyIsikKszIDYxHdn5eoQEqBAXF4dTp8ggPHr0KKKi7LSK3E3fCTzpii0Zibsr9Zh1nccpCpatO4jfzh/UTKpa9yww+aTrr7+0RRqrGfsLiYSeyNxGD3JvUI8mmMzNdZNZ4x3ys/xdEJXbMPq5A2447XzUY24P8TvJco3qy3Tiljfo2Dy4CqjkghBcZhIFMnQ5rA+nnAa6u1lnKwx3298UjIDrD+fEsb8n8XeoP5JMfsvfJCeVWbFck/jMuG3ynY9oMtLHFrhn5Cs0l6JMVTBbQtWBnBjp8nuLdDICIzxvS/UVjv3CkoMhn2t8x/vudVjs+xLY9javo5j5HH/sSUnM3cxl2QaUwd01gwb+gUXuv6cz1BsGbH+XvCijvuhmDBgNwPn1vO6i+gEbn2e/e8lazKq4QmpO3EOpWX0+r9fhv1MTXy7U7g8c/kHKcEUPATa8IBFle3xEUS5L3DgJ/NyB60ETCjx11GvuhNs1eUEAwoPUCFJbp3QbNGiA6GgHjM/AcGD8PmDPTEaLnvSfbn4d2GdKA9n7cooTygDrPmp35Rtt1e8ubvRcy95d1OxOJrCvoA6ipPGlzUBoBXnJfKIoLVBbbH+f15sgkMyXfYMbdH4GW1tc0bK+ss/0PgYav9Mr5DXyJasz4j29gmzpBqOAT0tJmZUzK4HOb1ozqU/8TmU2s0O580OgooyOk0Ltvsxm2frUfDg6j7Xp9tPce725tfDyVgACnbDafd07hi+hDJAyLgqltViRKzi/3oI8JTIgKCp52hYTfKt1X6IK94/EPSRHlqkr37GNRmZ+7XUpLB1OqV+AEe+ts1yjN09y3PdDq50f//wGibSqy2FHiJxGvmZ34JH1bB+s2okcnKXDpM6Yza+zlGU542T3Jya+msg1HrsA6PiKV6fhlpEPDVShXVRpPNcnuoBOdW6uE4ZvmbrAUA+lbXPTgL1fcmoYwB7ats/LWzv2BlU7kLR2ZC6zDIN/cu/11bsCez+X+tWj7GuV37PQhMi7eADWe+d3Zs2xWmfg0Q3Wm8GhWRIJ0XamdF6Ga+9RrrGU7lQFsaNDbpStD5R9W7qvCgKQzv+LRqmDxIzAktJUMoWaghpyISAMaDgE6ONBTdUbzYcre+nomh2X9c8Ctc97dixfoNkTJDrGb2Oq3F3WdJ0BwNV9XN+ConjU73yJ0HJA/QfkPWbCbpZAdTlA8ydJCDZntLSm+e/mtXk9RnK8RIM0KMgZKrfh+jLvu75Y39U78waY9h0Lu6nUFMycBpfmujZqmfUOcjAq2w24VYCtXCoYXz7aAtXLSFKgYWFsAbp06RLef/99GG03VDmgUFt/GQo1rL6s4oYg8CJ8WwdMuyYRq1xFjW5U0mszFRi2AGjyqHfnc+cGcPUg00T/VvzzKpCZbOqhPsQI1xKRtSVjCJGetDqYaXdHhC5tNjC/K/CeijXYkLL0xBuMJqO937e+/ETEyKVc6KogCuKUqGL9eKOHmNbXhLHW3fMT+d47sg7wwELq6BclVEEWpFEUdGyKG+pAYOxm4G098MwJILSse69v+zwwcA7/HbMJqNDMu/NJuwwkHy1aPfiixp+PkzAoGoDjC9lubYYqkGUdMzThLEdoQikZ22OG/WOmJwL/q8P1vfxB9qQPmseyWJ8vqbTpSwSWAAb8wHMMjODEOVsj3/Vd6stoQkmAbTrO67f1uoWuWrVqeOedd/Dee+/hnXfeQfPmzTFwoMw67AGh/HLWTWb0Pmyhf46u9aaeXauXPK0t8TvoAQtKGounjhbO9NVmM4pKOcNaI0Re+MWt1uUM5uFHvGNtJABg5HLgr4lAVhLQ9T1GU7fOsiYfXsn+MQ9+T5VG0UC1v92fAr0+ljxxr85XJNtZn0c9AqWDpVetE6UsHUGhZD3YU9U9f0SllkDLp4ED31A/3hXSaHHA0/UtCHTcvXXeAeDwHNZ1BQUj0TGbCs9oZqdwCFXCDl7fgREckuXvZEjb9Wx5X6EAxm5lWl4UKYFdtiH3sPBKjufCb3iew9JEIzu7zqwCGj/Mm7fQa1luCggDqrR3fK00f5w3RwiKAB7f7v35WEAWxbt3330XMTExWLNmDRITPeiJLQz6fGDXJ8CtM8Cj6z1jpvozzH2m59aSqNHpDe8cmO3vSvU/0Uims6NZztoc9tHeuS612QDAH48xvS63Ypec6PkJ1aBy07jAG9ks1LDywMM2QzjK1Cv8mLocKQUoGgDdncKf7w7WTmZ9TRComfDYJu+cwsQ9wMV/WCqCH/9OzpCTyms2PxN45qRrSm73ErQ57Hi5EUstd1daqArD1rekOvLVA5SMdaT0mZ7IyYlGndRffyeXHRRTi3AQlCcYNJc8DYMOqPcAydqWKN+4YCuuswyqLsfaWfBSZOYujEbg127AjePcz1s9XXgnlTOIIvftG8dJ1qvQ1KvTk027vlIlB9GRt1g/lZujPpe9hk/FAKXr+Oa9igMxP9PI63K4EYSW944oE1KOLWvmtpbCaraJuwsaeIDEr7mtOOtYhpqQTxBZG3gpGchLN7X+yVC+afU0f4/cVKbD27/s/TEBLtojcyUH4sputmPZpuJdRcIualrr80hsrPqGPOdZHFjUD7h+jNdr3F/Ai1fti6ncq9j4ItUu9Xn8nKWiGIF7iqBS1FMAaLAKW5+nljFTZ+YymZF2EVgyDBi1wn94Tbao2QN4NY37olyaAz1mmOapaPk71HciJuQqUs/xtzU7DQe/987IH5rFcqQuh+ThJw9ZD7pxE36Y87ZB4i7JcxWUHCSgK+LZ477EjePWzPrrx7w7Xr9vqDwVWJI1psL0vsMrWwxEsDGSt+KkbobiRM5tzrrXaws+plAyNScIZMIf/N67Pt3QcsDUixSaeSGBw0rkgCBY98QKSv4+nuKCmRUsmvpvd3l9isWGG7EmlTiRm2/Cjn9XrflajMW8AoEpZW8wajnJf8FlKDpTmBKgpZCKrf7Fxc1AnA/HzbqKzGR+J/bGWqs0NPCiCMT9DRyaTb6Rp6jYnIHB5FPAU0fkcyZDLDkaAhBmR9HTHZxeYSINi/zs8du9OpxskbzPUH8kmef6PEacW6cDe7/gj+RITMDfcf04ySSR0UCDBzmAwAzbtLMZei17dcMrFd6iF1oOGL/HtfMoW5/DgXZ9RE3p8Co8L9EAwCi1ehQXEvcAC/vS/wirBEw8JGm9374I/D6Io0hr9AIubTQN1lECTx5wvw3MDKUaKFVTto9wF49uBNZMoFHu941rc+wdoUp7a1ZwuSYANsp2qkWKmr1YyzTq+HmWDmdXw+M77SvL3Qu4uJmOWLXOQKtJwDqTZoZS7Zh3o83mhMGI6o75GgCnxrna8lp/BJ2Mk0uZPUi9AFw7JD1u0Ll2HF8hZj6w9hk6INW7UbPDXKpM2EVynD6Xg3Qubeb63v4OMOWs5xlGTTCgkVkiObgUNec3TSO5boiHXWRmVO/GgUy6HFN5zzv+hGxGPi0tTa5DWaPrO/Rc934OXDvCD27Q0TB2ftM37+lLpMUDP7Wnp6YO5iS4Jw8yEq3cFihnR9M++xYwtyVbQ1SBHB4j13zqZuOkmv2dG0DCdqbwQ8qRDVyc2DJdqounx3PKl1k/4M/xnK4lGoFza6RUuEJFfoOtkT80m6lTZQAZ7EU966BcQ+DJ/fIcq84AbiRnVgM1e0CXUQvATJxNzsTPOy7i8c41IcgtauQrPLiKJZId7wN3rnFTTzlFueVomQm8RYFLW4AlQ7hPHf4BGPoLHbzUOKBWH/ukz+vH2Q5q1FHlcMIBeQSBBAHoOYM3gGTSX7ux66Z8E/nbWt3FplekLMelLcxqmuvPS4axbAYAcX9Kr1GqyUWw1FEQRQqQHZlLmedHNzjn38iN2n3l03bo/CbZ9cmH2ZodUR1YPJRqoZ3eABqNdutwshj5OXPmYMmSJQCAMmVkVqMTBH6o5MNM2xq13Mj9bVyhLU4soTcf1df6R0k6KKXOdDk0SL0+LTzyjPmJG6BBy9fs/hgY4mYvvisILQc8d4GM3JAyxV+vy0uX/m/Itx50kntbItEICkmeV6lhJGiJOykkvsFII7JsJPCGi73y/oqGD96VP173JdsH83QGLNh1CdXLhKB7/SKaMOYtVBpGuyd+p3NpTlEG+JnqnSWMBuDA/7gfNR1n3X1xaYt1+e3cWmDYL0C1Qnrjt71NkSaA+u8nF1NaWG5UaApMu8FBNyFl5Ve3dBdm0SeAkriWQ8u02dL/BQUgqLj3G/Vs9bTEpS3A4dl09DMSOSvjyQM+PXWfQqG0VjZc2MeU7dIDfz5BB80NJ8brmnxSUhKeeeYZAMDEiRMxbJiPZpB3ns5WG1UgW5BaPOmb95EDp1cCa8aTcLNmPAcVmFGxhWSc1MGutc2pQywUt1QkhfkKCiWZ6cVt4AHHrW4A0Gsm+6vVITTq7V5kmqvv1wU96vitACxZtTKy5p0h6RCw6jFg69ve6xbkpgF3bhb48/UMiSWsM4hIun0P6iMM+YlkKFUQp/T5QphELmx9i2XDY/NJHLx5SnqsWmepz9/V9R0QRiMGcJ2rZZxHYAuVhs58cRt4wNqRUwYC+RZOffcPuNergliybTaOI1hHry5YTju11HpefXqCT0/bCmfXACseBg58V1B0y11kXaduvS1Sz0vcKYXK7c/ndSSflpYGo9GIihUr3p1E5xMERbheay5uxG+39uYvb5UUoUrVot54zM8sQ7SaXPD1Oz4k4z6oFOtUzSews+DyVnpxXd4u+Jp/IxqOpsqYeUpbTYsBErX7khx35wa/x8LqmIB1x0G4h6x2d5GZBPzSjaUZVSBw+wIw4nfnr7OHQz+wPxoA2jxrxd7tXK8cfgegEAQEqpXoWs9NsRZ/QGRt4LlzxX0WruHSP9L6FgQ6cuZMXO2+wIglVGSr3q1gatVooNN3ZiUj0kc30GG9fow6DrX68Lr/L6DBKODIHBKplRrrNrkO0/i4Ps8kbFWIU2JLYq3czjfna4v4ncDKh3gtxP3JTKunU1H/msQZCQAweB7QZIz0WNupnLshKMhFqNrB7iEcQbaafMmSftpq5Qoyk4CTS8iKbPCg90I7tfsDR39ialgVVJDhXqmVYzJFyhkaeH0uhVxWPgw8exYYc48Sq7xBk0cp3mGuwVVpa/14SBk6VHtmsuWmyWP2N4PaAzhFLjOJWZRBPnRGLXHzpJQR0eexZdETiCKw/nmpFerAt9SHNxFP61Vk6apqZDAWT+mAsuF2tPz/y7hxgvrxFZrJIzhVdyjXqVk22XbTLWxQ1OkVJoOQz4FHm14CRiymkt5/Db0/J5EwLZ76AWEVrB8Prwwc/JbE4CaPcY3bQ8tJLGkatCTe9pJRBbIwJB2QyIu6HAYknhj5tMvAsV+l8sW6KQWNfOW2bLut2VMiH7sI/2fXewqjAfj7abaJVGpNgo+9aC83jYIR+ZmUy0066P085Nr9qCp1eRsla93ZWLR3rNtdtEWYWvZHRA90TMCK+5v1N10OIyNBYb04zAgIBZ4+TuGQElUKbia+QoUWpnqiksJCnhKdtkwv2OusKDiCMiJE898x8HmZZF9fj2Hk2+9r+8+7cRL4sZ3E1xg42/414g46vUEyVMppppIja7v+Wu0d3FVqFA2uz1H4N0KhAJoVov628wM68LocOkeP77Iv/FOqJjD1EjMhkdHy9dU7Q40egPJdZgjVQexmcBdGA6dOGizawpV2xK0qtwHgmb7Cv9fI7/6MU7EAproX9aX+tC2Sj9ADNN9OLffeyAOey9RWaME03+UtAER5zkUuaHM4Aa1EVfllhW/FUcGtfBPX67GJe6zLIhteIAu/8/SCEb0qQN4JeK4gpDQw8Qhw4jdGJU3G2n9eTiqw5zNuFu2nWY+WvH0J2P+l9fP7fMm2nf8yVj4EXNzA/x/4hq1L3d4r+LyLmxhtGfW8nVjsvZEXBM+V6xqMYqdQxhVmebp/4N25yIncdDohroxpdRdX9pM8XaOb6+2tliRGfT4Z9z0/ti9DG1jCO5EhT1CxOTBuO8mVFVs6DkZSz5OoGVyG69uyP//c3xzQZIagZGZHRnht5G/fvi3HeVjj5DJg/XOsYw7/ze0aBACqilkiyQHbsnRdSXxDGcCovzihUFCO9fZFpqqLeliIIyQdAhb05IZZpj5nYrsyUtegd14vTznLFkGjgZ9/yHzXtPOjegMH/ydtBLmp1JuPqCGPTrgcKFXT+Wjl+V2omgWREcvUi1KaXzTCSqgoKBJo/YyvzrZosP19YP/XdBZH/1G4oIsjXI+1vn92jX0jX6E5rz+jlkQ4T/YSOREQRrGltIssD7qZevUZTizhUBgAqDecg4pcIee5sr7j/gZWPGjSsVAAT+xxTaq13jAOptFlM+uRmQj89ST3Hy+lXmVDYaVXgJmaea35r1LDTPEjf0uP2wo/Ve3guCzhIbwKx2JiYjByJKUBq1aVSR0sNx1YPZbzvzMSgMUepjhbTrK+74iMUaIyhzzUe4Da0sMWePZ+ckIQ2AdfHAY++xZrZLYKVP+8ypKGPpdpsbNO5jVrc2i8PtAA39Ylc9QRLqxnj7AhjwbbTEApDAY9HbKH11q3zOmyOeegOJCXwRJNZpLrr9FrmfY1mqLNO9fZHmhGZBTZ5go1nd7B8+Q/76LE1YPAnk/ZxnXzBLC6kHRtYWjymPV9RzXwGl3pNEYPBjq/BXR8zbP3kxNKFTX6i8PAZybZX4vrnyNvRJ8HnP2D12RhyLgKfBPF9f1rT0bajhC7gOvafPzza52fpz6fe/iQnxkBmyEogdvFNIY46xrXd64bmjCp502OusiSUaKNOmX0INbbFWoSCPt+I+spA15G8m+99RZu3ryJ2rVrY9asWa69yGjkPPizq9luMmCWtbKVLtvawORn8r67LR/RA4GRy6iOV64xW6scoWp73v7riF1ETxkCL74RS6TvXWNq4zO3/6mcRPHH5jP6h8ioZfs7jglv5Rqb+ty1PK6zbEr8TuD3AdwwGj/KEbC/9TOdn0jyZFEj6xq5Hfo8eudjNroWNao0QPmmFIARRXIGgmymaPX7mjPMlRqOPbWBaE8StLiQf4fXUPIRoOlY1q8t125uKu5mJkQjnXlP0HMGmcanVwBR/QvPljQc5f9TFYsCm14haRMiR5p2snB4VBbXlWi0vm8PW95gaQwicHUfELvQ8cyNSq1McuQ5PK6tjoUtjv5EJTxRpIZIt/dJUITA7GGN7k4/quxIOsROGYWSBnlSjGuzJ0pHm0alK7h+a9hE6Uo1g8zcNLYUOsuKeACvjpiZmQkA+OGHH1C9enXXXnR8IXDoe/7gmVeZWu1ioVwXEM60mplp2HqK5z2dDUbydh+uYcPzkgLVub/pzZvrZ/3+R0WqzKuccxw9uPBjGXSSQ2A0WmvP374ELBnKY7V9Huj6Np292AXMuHSeXvix/3pSIiSeWk6P/8lDVESs0p5tir7G2T8pTCGK7PHOSGQkb75u98wEqv5Z+DHMGLeNNTuDnu1xAPDHWMqRRtbh9EUHmgEpKSmYNm0aACAoyIXyia+x+TUqExrygV0fA+WbAXX6S49H1LAQQRGALu94/l4dXubtPpwjNx3Y/41E4Nz2FuvDZqMy/Hfg94EMsjq96XwNGbTS+hZF0/wBExJ2A6se4V7S71tqWOjz2AnT4EHHWReADvLaZyRJ7X9eBV5NJVcn7RJQq7fjUbJyYvdMqjAGlWJv/t4vpW4KhYriTR1fdX6cgDBg4mG2CgaXZst0Xia/66SDnKo6erVPOTZepeuVStYNJ06ciDFjxmDbtm3OX5R2WRowo8+l3KMlYhdYDHRQUMr1PooGagtCiGi0vh+/g0p4qiD2e98dbOMAzR5n25oqkK1uXS16+1ePY+Sal8bU7dWDjPrGbgF6fOiZN1u2PglVRWHgDXpgxWim1fPS2OYYXIaLHyC3o4Qb5avAEoxEu7/HEs2ZVRRUMrdZmfvj7WDSpEk4fPgwwsLC8OabfiDznHpOMuKiAUi/bP34rhmSaIgqQJIuvQ/fQqm2DpbM0aUZp5fTUCs0Jn6IE3R7n0ZLGcDugsYWZMYlQ+j0Zt9k6VV7h9f32C1Ay4menX+VdiQ7hsisqGoPt86ZRnZnczbGyocYtZtZ70oNEOpGh07J6iQMtn+Jmbjdn5ja7/KZlTzkYhbcQ3hl5CdPngyVSoVLly5h0aJF6NGjBw4fPlz4ixo9zNRvQDgNRuo5qkalnOXjlheeILAGcx9FgxFLKHepCgS6vmdNiNr+Dp0yXTZ/M0tGqD0EluB88KmXOD7U8lg5KdaStO5u9IN/pOqfQsVMTVGTJc1Mbcv70YOA5uO5+Gv1Arp/5PnxC7RZ2VHBAhAXF4dVq6imuHTpUnTu3Nnu84oU7V6kcxgQTkNybAHnl2ebnHVBYWFshILT0e7DN9CEmNZNKCXBRy6VOmQMOk5w1OUA+hxqhuQ4IVSXrgO8lAQ8H8/x3+aBS6JoLU8riu61ASuUzOopNbx+es0seu6CNsv6uszP5AyV2v04CrzJWJYJPUV+JgMFABD1vO9DCO7U81q2bCnaGvG4uDjExMTg9ddfR3x8PL7//vu7MrcOkZnMub5rJkgbWEgZYNp1Sn8u6ElPJ7wKWdyezt2+D/kwtw2QbKqxq4I5Ec7TGcdnVjP6VSiZjh6/l1GdOzAamPHR+FACtDBseRPYZ2ptazNVXgGO/Dtk5GYkcrMZu6UAg/fChQto0qQJcnJyEB0djRMnTkCttu6dFwThiCiKLeEi7K1vj3ArjsI/656lY6hQk58wbhtbx37uxAipUht+Nle6NO7DdxBF4JMIydiogoBXb9vlf7iEHR+wVCMIQN1hwPBF7h9Dn8/z8vQcvIHRCCweTHEb0UjnyNOWSXu4fQn4sY1p/zKl88PdH0/r6vr2usofHR2N6OhozJs3D/Hx8a69KLwi2wQsI5acVG5uuz7k39s8T9KFOXVrNABrnpTEbUYutfbw7tyghnT5Jq7XbPZ9zclF5RoDg+bKM/np34oRvwPLRwFZyayZe2rgAaDeUA7CuXOdilfKgsIuTqFQFp+BB4AeH5H1LopMx8kJs3hP2kVmBuxcl5mZmcjNpUZ9iRIloFL5keRF6WimapVqGnmjjgpx+VnA5tcZSfadBrSZIr0mN53X17WjFJgZ8L21FsPtS3R6KrV2bQ64Qc+pg5f+oQJlr5n+MY/BHyEI7FJZPY5ZqUFzvDOuXd4CGj5EI+bpyGd3nX45oVAAD//FjGVghPwjzUvVBJ5P4PUcUd3njozXO0NWVhYmT56MrVu3AgDq1q3r2gsDwoGqHU0MbCMJOTs/BA59x7RR2kW2D7V6ms+PXcBBBGYt+O3vAX0+52PXYxkdCKb038TDzmuzl7cBW980vdclGgzLyW4GPXAjlunr+5kEfp9PHZHveOEVPfJe/QoR1Xx3bHOblQM0b94cW7ZsQffu3XHw4EEcPHgQbdoUsRhIYajQnBuk0cBoqGIL4I9xZFkb8oHNr1Jm1tyBsOV18j6MWpJzq3cGGj3Ex06vAlY9yvJMSDlg0lHnKdyD33EctT6Xm2lktHU9WJvNoKBUraIhcvk7qnUEpl6Q73hyjcIuLghCoevPa2iCgTIu2kov4VVB7NSpU2jWrBkWLlyI4OBgzJs3D926dXPtxYLAKrARXAAAIABJREFU4Qw9P2Y0lHaZ6U9LBbMUi37n7JuSTrAhnwMdMq7y/sHvWEfJz+TNlT7rNAtCkCGfvd9m6PKBr6sBc1sBX9dga9l93IefoVu3bujVi6qKffv2xalTp5y8ogihCQEmHQPaPEcjf3k722YtmfW3LYxKVrLE/DbqgSv7pLrwjvdorLVZQPZ1qtg5Q+o5vgbgXmLZW52WAMwsQ7nbzysCSTKUKO7jPvwUXhn5N954AxcvXkT16tVx5MgRTJgwAYI77W4qDQkWAAkfop6RuCaM4xYtBS8aj2FfrCYMgMCa/nfRwMXNlAw193UqA4CwQkaUmlFnAN9DE0aiUPtp0mO7ZnDTgUji07opDg9zH/9S6LXWM639FC+/zBay9PR0fPrpp8V8NjYIKmlyzvO5vmE0jUoOZR0+ymIkcKc3TOsxlO1Tx34B/lcLSL1Abo55FKsousZsbj6exwsIL7iX/PmEyQEw0rFY/6yMH/o+7glocwoX8PkXwSsjn5ZG5Z85c+a4nqa3ReloiW2rCgTqj6Lco2jg9CFzf3V4ReDZ80DrZ0kM0WXTQ9/xPtDhVSB6CJmPjR7iaFZnCC0HTD4NDP0FmHCAEopm5NsMjbjPAP5v4fQq4JMSJCP94wcKaYXgyy9J/gsJCcFLL71UzGdjB+UaW89XbzWZjrU2RyIuAtQdn3qRo1YhMmrPywCOzCPxqWp77gudp7smXFWxBSe7DfmZ67xcI+mxPFvFsvvr+z+FHR9yfX9c4j+RpZXl6g4MdEIc0GZT3OP7RiS7WaJ6FwqtVGwNNH2cLPu0yyRtXNjIEYIAcGETBzsElpCcAoWaUbw6EBi5BJh2jXV1V/usQ0pzznu5htZ/bz3FYhKQwPMrKmRcBWY3A2aEA+ueKygvex++x5oJJuU6PYefpCcU9xk5xNWrLFmtW7cOTZo0KZ6TyExiG+zsZtQpt0TrySTRVmzFaP3aERIu9Tls20rcw2s8dhFw6AfyX8xZOVUgnfuw8sDjO9iy1ckNp6tkDaD+cCDCRrOgxwypNVdQkuRXVEg6DHxVHfikJHBodtG9730Q2bc43c6oZ4bpr4n/+j1WHkruP68C5xVAz0/sTxDb9DLVuwz5wNbpQNmGQK2e0uPNx/MGAH88LqknGfX05s/+yZYrXQ6gDKTO/OXNHFTgCwMcGcWo4so+RiKl68j/HmaIIg2KKpDOy9rJnH8tGoCYn8kMrt3X+XF8hYwrwO+DgfRLzJD0/txzBcKiwpEfKYOpDqa0satT7RzCB5/3zk3qA0RGyzLRr2TJkjKclB0kHQI2TeP12f97+4SqpcM5YUw0kCH/bJxEVlUogZ4fATDpBpxcgrsdNYLA9b3tbRMfJ5e/WY0eVAOr1Qto+bT8n6l2X2o43DxJ4p8vRw+b17e5TXDZCM7kAICNL7BsWJzE3qsHgeUj2fnQa6ZjaVp/gSgCG1+iglyJqsDDfxeNAJa7SE+k/SpVs7jPRKY81dUDFEdZ1M++eP+tMxYqWEYy5x2h4yuM1jVhjOqbPU4jbybkGfL44758g323vhriEl4JaDDCtwY+5zbwQ2NgRigwqyHv597iZgmYNkE3hiEAXATXj3OOthz46yng5nESGg/P4fhHf8adG6yx5mcyYlzmwYznofNp1BQqirvYRoKeIuMq8HNnkr6+qMTJewt6SMIY/gazZkXCTo4BXtDT/vPSLkrXrEJFuWJH6DWT5TZ1CJ30mj2pm6DLASCyNNZkDPDKTU6gtJxrISfK1OX69qWBTzkDfF4emBEG/DaQv7NlKVBQuC+EYtDTMFsSh73BsuEmSeY0rpvMZHmO6yvE72Dbsy6H5Mo1birohZSm0JdCRT7YkJ/kC1qSjwCzGgGfRgL/iwJmNWA2tpghU3OtRbojK5mEG0u0mUrPXFDyy63jYO4uAJSpB7yQyOEHpaLoAVfvIrXP+cO4SLmw/2sKh4hGypd+UZGT8K7H8sILLkuZyZhf+JwGoyRlKUf4ayJ1lQGg+ZMcbuINclIt1Ok8cDqKGmZn0AxbtS3RIop0hLpDgNez6Il70sN6bi0XfFRf6xn2f4yhM2w2iDo9I+Are3iN+xtyUiUNcYgUsLE3LKrVFGDvZ/x7WEW2zzlC7X7ACwkk5JWuy0i/Rlc6Cvpcfjflm/nqExUt1j9PKWiIbB2cWRpoOo5RqKAAKrRg//+VvSQI1h9ReC+/QQfM78wMhFEPDJxNOWhvkGfjdGizHD/XH5CfIV1/orHgfuTKMLNOr3FmhkLpvkaH0ch27syrVG+1jNQX9aOa593n6oDDszkMyIfa9M4gj5FXBgEaJXvdI+30FtYbCkzYT8+2ehfn4gIBYdZEmSaP8Qe9tIWDUaILcRLuJZiNpxmGfODwDxy2cn49pWTNc5jVQcD+r9iW5GgjyMswOQSmyPDANxQU8kZYoucMqj8JCqBENaD2AM+PVRSIqE4xldMrAIgsIZlxcBYFUpQaSvhaDk6xhVLlmYZ+7ELg70mMgnd/CjyxkyQwgBuD2cCbIRopDuMhbt92Ij/qDcIrcULeTVNWqM4g+xtot3eAmt1p0KL6OL/eQspYa5D3+ZLOwa2zdEx9mT0rSogGWAVA+RnsGpgSR1Jx7ELqvAsCsxtnVwMjFjs+3tUDbB02z/bY8IL3Rr7HR8A/r3B91+pDBUp/RlRfOocpZwCIzAwBNO5rp9CBCi3P9mxbrpUlPBWg2fiCSX8hnxyx587zWjYarUdEm6FQFq+wD+Qy8t3fBRpVpQF2tDGWa2RtuN2BIDBt38zD2dP+irZTmaGw7BeGwIvi+EKpzxeQRHvS4x3XoFSBBY1I8hHvxujW7EF96swkqldd2cvUbdWOxcsVcARBAIb9StUtdbA0vS0nlQbekM/bitHAGz7QjD69QsomGLV0TM1GvvN0TtiCwAhZoQbavwJUaOr22+j1ekyaNAnJyclQKBQoVcoHkYIgAOO2U2VSGVB4Bs4b3oNSDXR63fPX+yv6fsXI23L2gC6HNXjLQVyiyG6h0ysLP15QKYvhXeBxc9OBoAjPz7HNs9y3tXeA0vV4/V4/zsDMfN36E1QBDBhvxTFYNAsZJe4GYn/l/peVBKwZDzx5QP73P7vaOluYfIT7oEJBkunRn3gORgNLUoNmF68yJ+Qy8pXbAo38YDjGvYaQMvTq930JbH2Lm2r0IJYpNHbS8go1vVRHUAWw2yDziul+kDQe0dvzDClDQZPf+tP5UAcDDyyybj30FwgCJ2NZwqCzua91LbXnLqp3BS5tNpFENdbDc5qOpV57VhJH4rqj2Z52meNogyKBdi9g89Zd+Okndp4MHjwYlSq5oA3hCVQB98c1e4pyjYCXU2hwTi3H3TnugsD5D5YGG3AeRZepx5Kn2ZFXqi3EhbyAWblx/zecE6/LAfZ/CTx50HNZWl9CoSwoq63LtV7LtmU7uVC1I6dEmrtvLL+fvl9zcI0+n+vbHULt1YN0/MrU4+hsGSWY/Ujw+j8KhQLoMI39/dpsGidB4CjHRX2klH5gSQ7zcOYVDppLMg0AVGxJoyMXLm6yVhE7+6d/GnmABKKbJ5luDi3LNqyWk1gjA4A+X/mmS6Dt83TGEncDDR9kvdkSZeq6L2epzebAmpzb3NgTd6HLiNV3H16/fj3S09MREeFFRHcfvoFSRS2Ozm/RYTIz6du9wHKceX2XqgOM2Vj4sQSB5bctb5qym+Pl1VU/s0oyjqJIkps/GnmA42AzEmhMNSFAje50oK/s5Xfjq7bnwT8BJWtxhHLrZ607IwShwCApl3DrHPBrN4lzlpnEMqlMuG/k/QXhNpFYrZ5A9w+BvV9Q8Wv0KutxrY5Quy9Hu+bc4sUoQ3vWXVTtyItQl8NUVA0XJYyLGteOAfM7mUSMBE7Mi6xNEmLH1xhh+4oIIwgcvNJGRpXE2xdN6lxGRm6JuxETE3P34YEDB6JECc/r+vfhYwhCwdbDjq+xTBe3hoZh5HLXBmS1f4mEL4NW/tkJNXuRCKrL4TlX9qNZCJY4tZy6KwoVZ9pPOsbv7rF/2PIbVMo5QdlTqAOB7u/Le8ykg5Lgmi6HfCy/M/L6fPYF/taPdeNGjwCD5/l/P7UnyLjKlHXaRaZmBs52/XPqtcCG54H47ez17/5B4a/t9LpntcqgkgU7HORAnf7A0F+5MdXobi0V6k849L0Fq14BHPsV6PEh74YVUu7wV5SqRb6FLoeRfLXOiI2NvfvwwoUL3ZOTdgd5GXTsrh0Flgxjy1f3D4F2z/vm/YobSYeApQ/wc3f/gLwZV5GTSiGl1POUyW42zvFzlSpg2C+enaOv2v46vUGW/7UjlBH3x5o8wEFmd/lKIjOMDUZwL5Wr3bUoUbmt1PWjDqZ2gozwzshnmGq/v/UH4uqTHSsaKXhRd+i/hwVviXVT2O4mGoDjv5GMFD3ItdfumUl2rT6X7XNl6sk7p7go0GAEb/6MEtXJR9Dn0jjq84HFQ8i87/6R77x8X0ETwmzEwe8ZpbR5Dp3OXYJKpYJer0e7du2wePFi1KtXT773FEVg5SPA6eX8DtXBbHsDODGu7lD5R+z6A5aPkvr8N79GUporGTSAmvjn17N1at1kloo8IFUWGxQKoG3x93U7RUR17sFGPa/TlNPAbwOYuu/42r03UjgyioqOx3+jTWg2XtbDe27kc9Ml5SajniptVu0iPmAu+wPy0qwZ7JZ9ps6QGmdR0861YdXfh2zoMI0CTAk7gGqdgcOzTFFwAB3T0auK+wxdQ3YKVRfL1OdG0Hvm3YcaNmyIffv24aGHHkJsbCxatGiBVatWoW9fmToeruxlxsaoZ1bEksgkKArqD/xbkG/RJy4orO87Q+o5Sa1TULIT5l4y8vcKBs2lA3r7PBDVD9jzKa/P+O38ze6VTo20y7Sbldswa+KjzInnBVvb9KBCxTqtOgQoWZOCIv9G9JhB5rsmlDWxukNdf23LSYyINOGMzhqO9t153svIz6IT5ClUAcDwRcCLV4AmptodwHp28iF5ztHXyLgKfFcXWDWGaogzwqmcdnT+3ae0bNkSR48eRbdu3ZCbm4vPP/9cvve3HcoUWp4RvSqIG6u/ErK8Re/PpMxFzV7utf22M0kpa0KZ9vZXzkpxIzetYLeLOwgtB4zdTFGlUlF0RAEa+sQ98pyjr5G4l+p4f4zhLIMPg4GZZYGEXbK/leeRfGAJit8kXOImOuRnpq2zkoFStT0TErkXULUDFfmyktny4o5iUtUOwKRYClpUbguUqOy787xXsfl1kg0FBa+pxg97d7xKrUi0U2rIem/woDzn6S5EkZ67JsQ1RvSZlWTVm1ukzP+ufZpDlQJJtAsLC8Pbb7+Nbdu2QavVOjiYB6jclgqLsQt4zqNW0HnPzyJH4N/ItwGoxRHVl5nIyDrufc4WE4AKzTjQqEb3u7/RfZhgNLBsdnET20fHbPKe3BfVF9j+Lv+vUBVf+dNoYGY2tLxrv/uBbwu2N+tzWS6adk3WU/POEodXAnAJeHQj0KQ7/1YcF7YoAlnXSDZzp/fYU3hDbIuMsj/k415A/A4O0FFqSKyUO72UmQzs+0pKef79lPdGPqgk2benllFDoFIbYG4bICMeaPsC0PFVytDmZ3BcsS/q9aJI8Z24vwCIQP/vpIFMjlCiGjetAn3QotUc7Js3b+LFF18EAAQHB8t3zoIADP0ZGDDL5CCZIns5W7ZchUEPZN8AQsq6L0PqCcIqeE5u82Ha1eeI+YVKfOFVgGEL5A9CLv7DEppRB+TruJc8ddi7Y5ZrSHGcixsph6wJBf5Xm5nAfv/jgK+zq5ndix7sm3q9Lhf4qT3LNRCotletY+GviYwy8YVstBJ80N8vk6ytC4fJywB2fsSadvuX5ZOu1GuBhb0o+ajUAI9tttYLvw95oMsjucXsfS7sA7ySIm9EZ5sitr3vKcIrsS8ZAH7tAVw7TILozg/YvnLxHwAisGsGHQJbQ2I0cqrd6RVA5Xbse9a4YVBvxQHn/pb4GJumOTfydYeQoX18EVO/Kaf5XTefwL5/EyZNmoSYmBiEh4dj+vTp2HHmBj5fdwYBKpk2M1flP9Pigd2f0Mnu9KZ8g6Pu3AR+bMthQ0GlqGJm2256H94j5SzJgrocZpxWPgI8sUPe97A1sAqZsr3lGkoStp+VkwiiKx/mxNNbcQBEGvxRywq+Pv8OsHos94KGoymV686+FvcXo3izgd78KjDeSdmg05vkByXsorFPv8S/9/6i8Nft/pTiaSVcb5/0XU496xqwbCR7fNs8C1zYACQdYC3m9EqmvOWIms6vY3uPWa50w/PAhL3eH/dehplxGhAu3xhLbZYUYQN01owGecsyYeUpR7v9XW4AQ3+V79hmZF2zGLij5PVjjpbTE7gh2Gpen1wMHJlHByfuL56fBQnOKdTB1nMK7KkZ2kIQgG7v8mY+b4OuQIvQ+fPnAQBLly5F05ZtMOCz7cjX28xE8AWuHeMmqr1DgZYNL3A4h6AELm8Dnj4mz/scmkW2u1FHQ7/3c8rF/peh13J9h1eWz5nKSuJvB5BYnBEvz3EtUaMH5x+cWkpxr4Gz5X8PSwlhgIJY5vV9ZiUddlvtkK3Tmc0z5AOHfgAqtgIajnL9PTWhFpxzBRDggiiVOlBqoRRFkjTVIVYOfAEkHQJ2vE9nIvuWy6cno1KKDdY8CVzdD2RfZ4SUdMA00UrkgjUz8+0hPwtYPxVY8gDZxYVBaTmKUqBX5CukXmCv8OKhVCnyRxiNnP8+rzXwdU3gm9rAtne9H2caXJr1L00oL8ZmT/iGd9H5TeDNHOCNO9TPlhvdPyB5TBPGkcWRtaXNDYL9KDEzyaI2nscF6Q4iqnJQjjoECCkH9PuWv5M7CKtQaA9wpUqVkJ2vt+xv8S0WD2YHQ+YVYPXjLHeIRq7tmyekvl97yLgCrHoMWPkop7AVBlWglNFRKNkh4Ssk7GKG6o9x7Hn3R+TfAWY3odjT5xWAWU2Boz97f9wq7Xnta8LolHZ8zftj2kKhAEb8zvX9SopvOg86vCaNMq7VR7IHgoJlCHviYOnx0vo26unwuIPa/VhWVAYwDd/lbfdeLwhs0yzMwAPMUNzdq1zfP3wXyVtO3BIEoGwjIOUUv8SAcKqxOcLKR0jOMOTz32fPAeEV7T83qi9QZzBwagkQWoE1RF9AFLmwsm/y/1f3Ay8ly6soJwdSTgHxW6XUUdoFpqUVKqDLdM+PKwjAg3+wpqZQez/u12igZkDmVYoKWQ7dcaXuenoVcHkLf39XdQoAoP5wyv1mJrF2mp1C7YPc2+ycsMe1aDiabTpGPc/bnPp3B22nkow1vzMj4NLRwBN73Ev7O0HZ8EC0r10aBy6kwuhrc59jGUkIQHAZRtoKJfX6HaU7RZHfQYZpbO3lLVRodFQrbT2ZNdWkg2wl7PCK7B8FAJB1naNCddm8vjMSgHHbfPNe3iDuT3535rLZzVhyV8IqejcwSh0EPHWUvJuwikD5xt6dZ/4dzn035AMtnrJWmHQ2lc1ooPx0yhnTvAc3pGK7v8coXJfLkcfXj7E8pgoC+juQum3/EudNKJQmcq4bUTzAa33QHE7oXDEa+KULy20jlshbzqzRnYFJRqKpo8C1DiTfGPmEXSQUCAp+uaEVSM47uZjplObjC6/1JR+SPCuFkv3ljoy8QgGM+A14YKFvDa42mxubOe2am8pUpStSlEWJgPCCI2xFI9PS3hh5gN+vXG1B66cCx+bzOtn3lTSy0RWcWsEami6HjsLI5YWPjbVFRDVJErREZeCh1U6eX5WOZvIRilV4WgLZ/LqUTkw9x7SlF5MVRVHE9evX794XBAEzRjVF3LVMBKiVqPWWx4cuHLGLgMAIIFvLSKlaZxK1js7j/RZPOX6tPp+b1N11dJvfiXmamC0CwoAn99tPs8qJtEuSo2HUATdO+u69vEGgHSfUqOesBG+nQqqD5JssubAPlfNEEYiZD0w54zrpbcubwMFvpfU9KabgwKnCYNneWbE5MG5r4c+v1gmYfJp2pkILzyWv102WeDfn1rKMLCcJUx0EPHWE+1BYReAt10Sa5F81eRn0iFPj+AMHlQKejgVCIqnn3WW6c+Zq/ZFMtyg1TE+EuyBV6OuIOiAUqNJB0gKo3JYbEEDZ1OUP8mIuLE1ZFIioxvnctqS1Wr2K53wcIW4NF7F5s7921PXXXtwkZSp0OUB8EURcwZFAVG/vOA7qIIvfRfAq9ay9fgaj+rbHrVu3oFarUaYMHSSFQkC9SiVQs6yPVP2uxTByvHPNpG/eFnj4L9aGO73OLEdh2Ql1IFPDqiDeImowenIGX6/v8k2AgBJMVatDODAKYJlr18fA8tEmgmYxo3Y/oKkdx7Bmz6I/F0cwGoCr+xioGbUs6ZjJcK7gwgZpfQsCszi+RkRV7pHezLSwWs+id6WlazEMZnJsZtSrAjg63A21SflXzp3rkFgIIn9cd9va+n4N9P+WXqshH5jdmIZ0y3QSoIwG58fwBcZsZDlgwPdk8QsCf4i1z7BFa80E4PPywEEflQxcRaungYmHuWlBAGr0BLq8U7znZItqnaR6mVFPFqyriOrLzRjgvzV6yH9+vkDvL9hrLii4KbubFjTj6gGsfK4ZVmzaDwBY8O2HKF++iDT5b1+Q6oJGPXDnhvttSWM2kV0sKFg2+aYmcHIZsPkN4IyTrIqvoAlhxNjnK2YF+33Dv299E9jxIbMui/oCX9cALjiZFudLCAIw4Ftg1EpTEKTg5EPbaYfFCYWS0bRCzWslsCTLOa6i9gBpfYsi217vBTywiKOgFSqgzXMFCbyu4tgC4OeOlEn+vr7X/BC30vV6o4iTV9MRVS4MgWoHC7tUFFC6LtORouiZOIHClObXZkse3Z/jGfWpg4Abx+kEuIKTS8meDCnHxeuqDrU9qAKApjZDWRJ3WYxnNNKp+edlSaqwuFChGfBaGsmOzmpgxYHBP1FsJC2edVd32qLqP8CN5PJWkmvkSjH6GhFVWZbwdo790Z+Qns1y1pjGwOiat528wEXo85kKLN/UseGu0Z1rUBQBGD2btqcOotiMPpdrRpdNnoJo4OY+YBZrsc4gimzLjfmJ5zz0F+90OoIjgZYTrf92eTugt1jf6fEk3067VrxiN/UfAOrmMOBRaZw/v6gxdqtpkEw+B9+4Q9Lt/gHXyq2z5OvcK7oiVdoCr97yfn3v+9KiX14kX6Ch5yJebhn5izey8NyvhxERrMGvk9rZf5JCCTyxm33BmjAgqo9nZxZUElJGQMEvTRT54c/97ZqRT4sn81efy5rbshGsaciJ6MHA0R+tRQx0eeQlFLcohiD4p4EHmLbt6kV2oe6Qe1c62VsyTuloEzlRh5BAlXv1ysKQcgqY34XEucf+sW/ogyOBZ06xZFKyJjc2TxAcCSg07FYQlBJJV5dDop0rRv7CRvbm67KpQLnxJWDIj56djyM0HMXvxVKdTJ/PvvIqxRxhKpT+O4wlpIyUDXEXCgXQshBeh7/D6/Vdl50rBi0dywgvAlO4ma4XRSBHa8DtbC12nC2kxqIOAhqMZITl6Qeu1ZttWpowoExdqW6nCgKqdXXtGGa2L8Avyzw1T07U7AE8sp4pprswAvuciBr4E4wGiiwsGUYNA1mPbQTWPQt8URlYNgrQyq/oJCvu3AQW9AK+qkZ5XX9Em6lSd0PZhvZrtJ5AFGnMkg4C12MdPy+kNFuGPDXwALUzanZnS2bF5lLpRh3sen05I1HiwBi0HP8sN9q9yAyBVTnJCOz6UP738hXy79ABWjYSuLJf5mNnUar2i8rAppeLn5PkDDdPAXNaAN9EAWfXFPfZ2MfA2VTfLNOQqn1eirt5xK4XAEQEeykvKYoUFslKAuoOk+Z8Z6ewppG4G4DIOkfdwUwjHppFpr5BB/zzGlsfCmNkV2jO8sHti4wUOrzs3Tk7QvXOJBNe3iLJFPprn6097P6EWga6HEZoIWVZM3cH2bfo3GlCrP9+fCEQ8zOPHbeGKbyeM+Q7d2+Qk8qMS2QdoGx9/u2viZxmZdQD296mwl3V9sV6mgWgVJnq+dtJfJOblCYaPZdtNsOg48hpgxZo+BDJeKLIiFsTxsdKmXqKK7chG/nUcs69SD0P7PqEtebCunDqDgW2vcX9QtT7pr1OEKTRyn+MlVL3vggYfIU/xnAEriGf/xbWkmwPokjuRVDJgpnBzW8wo2IWkqnclm2q/oD0BBPDvaVEmP19oKRzsWI0RdnkEhSSC0ER9pX5PIRbRj5Io0R4kBr9mlRAhzpuECnsYdvbbJ0SjVQQmxJHY7P/K8kbNOpoIIb/ztRsp+nA3BYU3hCUVDB69pzjbIFKQ13j+B10Bio08+6cC0OpKKBqJ7JKRSMlSe8VJOyUyg1GAx0qV428KAJ/T2Kri6CgU2a5yLOSTSJI4EbgrpCMr3DnBqdA6fPoAD7wG8V3MhKkqVaCwn1hjHsZqkAgOAzo/qF33BWA0V3CTgAinfPx+4ElQ6iGJxr43RryWeqaeASoM4Dv/1t/E48kkApfowvJLIWWBaacpWZFqdq+rd1G9aEjn32T10cXX/Un+gBXD1i3JN8667qR1+cDC3ryt1AFsR3Nch/NiLcWksn0k/WSfJR6DAol9+PxezlR0JLlLwhshfY3Iy8z3AoBqpUOwabXuuOFfvUgWBjWlJQU6HRujg6MXcDUoD6XG+3FTTTwBi2Nu1lC1Rxd6nKp4paXJilrpSc4n+euCmDrky8NPMAL5tH1TN2P3wt0e8+37ycnGj3MNKlCxUXhTjtO6jkgdiF/N30eDb7tsTVh7N9XhzA68wecW8vrT5vFa2yvaUxrpzclRbzg0iwb/VdQtgHwys2C5DN3YTSY2qBMxNmU0xRxSdzFGrxRZzF4R6BjfPsi8NtAySHU5wEJ252/V1BJtpX5mpwVEAY8fRx46E/gmRP+E626gvrDufZZTFAxAAAgAElEQVQUat7c2Qvj1lBQxpAP5KcDG1+0frz9yzx2QDhvDUbKe+6e4uiPvP7yM6lnEruAf2/7ojQOuFJrOof/cnglhlOuHCdSjRgxAgqFAmPHjsWcOXOgVruQyi/fjDVzg5YeYOlo+89TB3OjTU+QhAbMKFnDv8Y5KpTOpw/5I5qOZffB9WPcMN1p/VCoAEt1Ndue54hqZJRfO0rFMn8ZLhJRHSw8ga1IkaaBSQ1GsGc6PZ6pel9Mpfu3Q6Hk95uRwEyPOoQlIKt6rQBeNyJTvMlHTFP3LB6v0b2oz7xwaILvzRnxfb/hd5yVzNKJO6UYq/Us2MiIg6VKs5BMxZbel3nkQmRtOuv6XNqQUiYnsMcHQL1hNP5VO/qfYqkP4JGR1xuMUCkV+Oyzz3Djxg0cOHAAWq0W8+fPR58+ffDggy7Q/YctAP55BUi/zFpa+SYkGayfauoznMq0fK3erMnr8uhN63IZNYdXYcT8b51r7Uvs+5ptGqVqAcMXkw9Ru69nrWilavH32zWDi+qBRQWfExzpf2I8NbsD3d6n9Gb5JtRmMCOytuuMdYPONRnenNssS925znRp+mXW1QfN86uNRhRFGIwiVEovz2ncNhKx9PnA/9k77/Cm6vaNf05GJ6UtZZSy9y6rIEOZIqjgC6iAgsiQ4UIQ1ytu/Qn6uhUHyHIjCoiI7CV77102BQotLV1pM87vjydtms6kPUlb9b6uXJDmnJNvkvNdz3M/9337VFEKbDVC5EoDKkKbMdK/I4fKawZ/shaLikEG4LzupX9RMGxWIboeXyIpt//MEV5DUX3WG/WTMfjoIgiqJr4LORFSs0BfhRJB+ydF0+H0anGfa/OI47WINq5fx9X+HXdKyjktaZI+MiVISqfTZPfbrjEU1Q02ZMvWbdR6wz/ickIa7eqF8f6DbTAaZDAYOnQoP/zwA9OnT+exxx4reosy25PX5H3zkuT3fIOh/ROa6n7/Y3BpJ8ztJmFUxSCT77Blxb+uzZ5n/acsujJShIV/cZtEAUasd5BH88LMW0TFKruTnzEQBswrUuj3iy++4LHHHmP8+PF88cUXeR6jKMpuVVWjXL1ms8jWatUH3iM13cJ97Wsy6c7GTmk5TVBQDfGVA2KtG9ZQKmtK0eKnzGDPLPhzgvRvgx90ft7hZFgc2Kylt1zPE0g4J+NkwjmJKA39I/9yZLMJPqxhJ1tnm08N/iKwlF+UuphwtX+71Yuu3UznSmIaKnDgfAIrDl7Oei04WKOwuaLkPwiUrwY9/w9ufe7fCb6ouJndUtJSsBugO9Dp/zkTPEjO78peQJXSrQ1vFHz8lX3OEzzIuWk3PNVCt3E5IY1kkwWbCkv2XOT45STt36SgeyQ8Uix82z7y7wRfVNy8JNETEF5DwhltrvtPmuABVr8gJZqowhk5+EP+xybF2InLOTbMiq5wzpgX4GadvJpNsFbFYvWCb/W/0BZ1b5f8aKalZBcvsITTk0Xb/6O6Yntb2mtpXYHN4tDdV1UHIz8/1O0lK3vFAChC/ClXtfQQlXD+WRQULO7a4f6LkkfkMElr+gZLpOiWCZ5/z8QLMLc7fNJQzIv+DrCanTtEQf07uIZwmvQ+oBhlcjcGQI2OJS+Ihps5+Url/SjvbyQt3UqtsEB6RxZiNPMvSh98ywlL+OJW4TVUbOj591z9Xzj2mzB0t7wn7N5KzSQ/Wy5chFFKqzJffmg9WkKjN06LCVOXKQUfP/hXKQfNSIZG/aXeumLjUvW5w0P88DPqsNpUOjesRLNqpYjU+i9cQ4W68ORJiTJVauZePXxRsWCQCCipNtGZqH6L6J0cni8E61YPl70oX8//kxLQ9JvST1s8mP+xeiOM3Sn92xgA9fpIbr5S01IRkXJrkvcx6PjjmW4kppoJDfRBp8v9w50/f16zxv0LD8EnQJT6vIUbpxwlU6pViGeLR0goy+ArA4Qr4g+mROl05auX/KDhHwKPHYLUa2JKUZg2t8FXjIM0gif6WaCvgeXP9yAtw0poYCnUQ/8XriGwoneJrtmtg3UGEZj680kJYRsDIOUq3Pp84ddJjgVUKFfFo811CRUbweRLYoUcWLnw8SYgzHNia8WE28sMg15HWJBvrgm+Vi3x537nnXeYN2+eNq1zB6oqEot/h1BwRiosnwTf3gknl5d0a4qPjpPttan2WvmwxvZBQZW84ZlC/J5BJCjfqwqfNoT5A0Uu19O4cgA+qAlv+sHqPHbqOp0MSO6Yb2iAb775hnfeeQeA2rVra3ptP6O+dE7wf6f+nXRF1PN+7F+wfHBZQefn7P07SELXGSmO38mcKpoUhWHj2/BhTZGTXveaR5ubheNLYVoovB2Ud5pBb5T+XdIbimLCLXZ9VFSUumvXrjxfS0tLY+LEicyYMQM/Pz/S0tLyPM4jSE+Ged2F3BQUIQY5xfH9LmksGgmHf5IJ0BggtrGVmpR0q4qH+GjZwVfvIDmrj+s6dvIN+sLgBQWf/2EtOxEGWSg8vEbCgp7EF63gqn0QNgbAyL8KL7+5GSP+2eGtPBaK9/f3x2QyMWbMGD7++GP8/fO2cnaXXV9Q/y5R3Dgr1pspV6UW++G17ttXlyZ80UpMb2wWyZ0/fbHs6zFc3iflobW7ikDWrE6OnXyXl+G2F/I/15IOb5dz5L11Bnj+hme/E5sNpgY5lD71vvB8XG5Z7pyIOyXRxPBWJR6K9wi7viD4+/vz5ZdfotPpMJlM1K9fn86dO7NmzRoWLVpE165d+eabb7R6O2fsmwOxhxyyiutccDczp4n05rRQMWYxmzzTtqLg0naHBr6iF1MFb+HUCpgaAm8FwK6vtLtuhXoiXRoQJoIZj2yHDk9Bt9fEArgwGLIP6qrDb9qTyMjGLld0kk8vCKdWwKcNpLTui5ay+HQVSZfFj2Hda/kycjMyMpg8eTImkwmdTseXX36Z7wT/t8LalyD5svTvK/thnwuRwpsxUrY4rQKseKZ0RQCuHXFMaDaLsLO9hW2fwFv+8r2cdiGC5iqqthKdDaO/6E48tBLaPS519YWF6hW9o+In87nOw9Ex1eZQV8zreV7Y8gF8ESlyuT/e4949dfWgRGe3fiykPi9C06WIoihMnz4dg8FAdHQ0W7Zs4fbbb2fgwIFs3LiRhx9+mD179mj5lkXHto9FLteUIBKc2z8p6RY50HK47Fb1vlK6UtOLKnoLBotIiSVNhIm0MtqJPQx758D14/K8YkPo86EMAAWZkGRi4LeSG9MZ4ZaJokPtafT5WBYXBn+7UU3ngo9f+5LsDDKSRPP+pIv6A1azTEhb34dNU2WRkAdmzJjBBx98AMCrr76KrhSQerwGd+foZY+Lip7phhA8o1d6pFlFQuP/SP82+Evksbg+Aa4i6TKsfl42EKYb8EvRPcpz4fxmWXwlXZHnNTvD3Z9Bm1GFh7v1BhFHMwbK4v0/s10bE4oDvQG6vyljrMFPqhAKU+tb/5qMi+YUOLvOMZYVhpsxEtnY9hGs+a+IFXkRmi+Xxo8fz7333svly5f56aefmDp1qtPr0dHRtGnjhuKQK2g1UgxSrh6QsiRXdONTr2WrJ81wNi4oadz6vExi8dHitFWQyIrWyPxOMlHY6tYVnNsE3/UmS0Z25Ab3S0uqtYNnrxa/Le6gUV8JpabFSySisMGqXLjDG11VRdnNFSRfgdTrjt1dzK48RWO6dOlChQoViI+P5/PPP6djx4706uVYEByLucmhiwm0rBlKg/Agdz5p6UaPN2VQTYmVftFyeOHnpMQ6POqhdLlC3vujuPBlJEOLB1xTVNMCOfu2RaPo5a4ZsGISoMiE+fgRMQ9yB80HycObuO0FYf7bLK6ld/1DHdE91ea6pPqVvRIJBFkkFHXBGb0a4k9Cw75upaM9shWoVKkSkZGRWCyF1A5rBd9ykrd+Lg4mnXPtC4h6FPxCxFTBL1hT5nOxoSgS2u4wwftykXf8T1a3el9oO0act4qLA9/KDtecIo9D84t/TW8hoIKYn7hCvun7pSxe/CvIzsBVnfNy4ZLG0Bmk1jYiKs/3i4yMZP/+/XTt2pWrV69yxx138PvvvwOw+0w842Zt59MVxxnz9TYOXUxw51OWboTWgUkX4Pl4cZV0RQir+xsOMlhQhMizlhboDdByGLQb713vjZBaUkdv8JP+3ftDba678wtH/7ami+V2WUFQVdcnzMGLxNAmsDL0/cr1sTG8laP6wOBfNNOr7Z/BT/1hxWRJGSRdLvwcOzya+Fi6dKknL+8MRQG/8q4fH1YfJp6RkEvFRqXL6KYkccsT0Hyw7OC1MpOp3FwG3EwiTuVm2ly3tKF8NRiz3fFcVeG3R+DA97ILGLpMcpc5oTfCmB0SzjP4Qcencx9jR/Xq1VmzZg19+/Zl+fLlLFu2jH79+rHywGXSLY6Kg3WHvRz18DR0OhF5cRV1e8KEaCFBVoksVXoEJQZFgXtmQtdX5T7TymK1Sgu4flQmeNXmMHv6uyGiDUw44XiekSLOiRe3Qmg9GLkRAsNyn1e+mvis7PkaQupC+8fdf+9MVz2QFO7Z9S6f6t3an9IGv2Co3r6kW1H6EFhJ2+u1e0z826NXQqN7XAu3/h1w6GcRyEAV4tisTvBiUt4SoUFVodc7Ll1Wr9dzzz33sHz5cjIsVlRVpVFEefwO6jGZrfgZdTSo+jcK1xcVQeHeTXWVFQRX1/Z6d38uC9XYwxLBKgUqb17BqucddsjXj8CcW+GJo3kfW6UF3Pmxe9e3pMvDr7x8p3HHJcWi2qCi69VW/+xJvjTjzHpRU2t4d+kQhygOdHro+ZY8tEBBJielCTft2teZsJiEOR9QodiXvp4k+dVl+2IYP3sHHw+PIinNzPbo69zWqDK9W/yrRllqYbPB8d8kJ99kYOFlW6UdvuXgP7O0u15Z6d9xJ5yfJ2jkAwKijzJ/oPAFWo0Qh1ZjgH0h9WTeEcF88A+i52qM1HgRtJjbQ9tSFBDm/w93i2rU580h5bq21/cGVFX7siVVlTKUN31EGOfyPm2vrzUihzn7cYc1dM9v+/ACeL+6aILH7HZ6ae2hSwDYVDhxJYl1R67ycJe6fD6yPQ90qq29e9w/DXEn4Yf/SDj2Wj67s6Ji8QhY+BAsfVSiOzZroaeUOniiJNGSDt/dCW8YYHpzB1O/tKLLS2SRiUGqJtzBhrfg3cowswMkXnR+7fcxQtKzmeHg90LCvutTGLEWmgxw6228Psn7+Xm4NMJb+GUwHPxRWL8/9sv9IxUHu2fYiSypcuOf26Ddtb2BHZ9LLe7UYDj5p3bXvbQTds+U1W3yFRksSzOCqsLTFyTHfvs0GLfH9R1KahwsGi6lePEn4QcHcSw6OppdS0VzQmfwARXyUJj+F0WFqsKcrnByqZRBzumq7UR8eL6DhBp/SiJ2ZQWqCksfhzeMsgDVUsNj/7eiF6/aJDS9thA/iJJG7S7iA9LuCeg3EwZ+7/q557fApmlS5RWzC5aMdn5d0RX83A14ZZJv1Ej8dLt3707v3r298Zaex9WDDutQnUHsRouD2MMi9KGqUDlS2K8gZUBliciSGgcrnhYSTkYS/DJEu2tb0pwnyUy1qtKMclWg9/tSFpkfK9xqkZ1jRorjb6ZEnHYJJrGkfeTF92nULJLkG7H4hVQmvF1fWtQMoWezf3PPmsFiEnW9TOllU4KonBUVNitc2iVqaQChdR2DtqKX6oqygvObYP88GZeSLsFvows/x1VY0hwsdJvVuT+UVlRpDnd/WrA9sjlN+rclWzlySqzjHlCtwpa3WuDnQSKjrfcBQ4DcH23GyPsUER7LyZ88eZKjRyXM9euvv+Lv70/t2rWdBTxOrRQf7vLVJRShNeHLk2hwp7CmFZ2U6VQtBtlkxTOw83OZwJoNgntmyIRw/Th0nOQd4RetkFPNyZqhXY6t5q1Q8zaJnqCDuz4r/jVLGqab8PUtItmrM4qGQHhLKRure7vo+qs2uO2/fPD5bGZNfQaACk1upceoF/n2qTvwM5ZSr+9dX4kAUrV2cMd7ZYfhbvSXsqerB4VPEhEl5bZFgc0G3/YRBrZqk4jOsBWw/ClZOPSc6l7VQEnDnHOhreFEHPkQ7JgufcHoL2qYZR1xp2BWR/neAsKk1DuwkhgIla8mCq02i2hBHPwBTv4hG6SEs9BiGPT7stj9RvNJXlVVvv32Wx577DEAmjZtSsOGDTEacwg+JF6A+QNkN6Yzysp5xDqtm+MZXD8uzGmbWVZc7R4rus6y1SylU5nCHQd/kAFRSyKLNxEUDlHjRWUMpBY3c1Cw2Vx3bcsLOj0M/QNuXrRrHHh5cEyNExET/zBZjGmhOHfoJyHsWOxeD2tfggd/l+9syGK4vEeIWZWasGP2GEAm+Pr3TcGiDyi9E/zpNVLTa04RkSqDn2gwlAUcXyp5eJtZfocuLxd9kRp7SCb4zMlw/WuifzFkkWbN9Srq9IBq7eHCFtng3JlNKdRqgbQ4CKhUtL6R6ex486JENzytepcT8dFwYqkw1+sXoZY9L2yaZhdiUiEpQ9KNXV6UPj1+n3BtylcXPZQdn2eLZFhEeVSDhbHmk/wzzzyTJb05ePBgvvrqq9wTPMCNM6DY395m1p7c4kmcXU8Wa9qaAaf+lB8uEzYbXN4t5hOF+bXrDPKDZ4YDFb12uuxXDkiosUYn7zql3fkR3PqCLIAymeTpSTCrszBS/UJg9GZRkXMXilIy5kPmNPiytSxSrBnw2ygh3mT/3YsCn8BsoVuDiDNlQqeDag7/ibBy4g5XoW5L/Ix6JvZpVLz39iSuH3PksS1pcHlvybbHHRxb5Fh0WTNE3CX7oG82yeIruGbh5Wj+oc7KewF51FEXBTYbXNwmpWv5iCd5BHoDDF8tmzT/Co7NTXy09G9TgqQXR28u2iJcb4DQ2po22SXcOCv925Iu85FfqERUm95bvOv6BskYbzPLJiX7d2LwhZqdHM9bPAjbPpTQvc4A3VzwYHEBmubkVVXljz8ctoKTJ08mODgfkZmIttIBjIHyaKNhbsfTyN6pjAFQu5vjNZsNvr8b5naHL1vBlvchZg8smwDbp+cm8CgKPPA7BNeWFd2gX7Rx2PprmoSJfrhbHPq8zeANCncuFds3Twhk1nRIuSY7mrKE2MMygGXWqVrS4K//g7Mbi3Y9mw2OLpJITr1eEs2q1Bh65b/bjYsTadaHbqvDksld6dqkFJdWNrhLFnmZeuRR40u6Ra6jVhfHQtsYIIvkTKQnieLYd33gs0ZS6nRiGfzxBBz+Jfe1gmtIHXlgFdkhDvpVmzb+Mhi+vUPGmT+e0OaarkJRZOeZPXq5/jXp19Z06eeumAiVJmSmxWwZCA8jXiogkosod56RKva1VVrKQ2eU+6rNmPzP8Q8RSeCxu0ROO7xl0d47BzTd3imKwuLFixk8eDAHDhygU6dOvP/++0yYMCH3wZnhiuNLJDRTL29TDs5uhGVPyIDRb0bBVp82KywcJoNnxcYwbLlnxDAi2sLghXIjV20jefNMxB2H8xsdpLB1rwKvSrjOGAAJZ6D3e87Xq90FJp3Rto2bpjnacHmvhA01ummKBJ2BLCKZojiXlpUFhNQml0uKohORm6Jg8Qg4ulD+H1oHpqQWGG355JNPmD9f5ICb1qtFcEAp9HzPjtA68NhB2QVXbi55+byw7xvY+JbsigfMK1hlMS0Bvr9LdtF1e8qE6YmQbsvhEi6NXiVyuNlLo04uk98805Fw+VOyq7WkiRumzQItcpBNW4+Uh1ZIuS7jZqavxO6vRGjFm9G6nNAZpV+rAIrnXeS0RpUW5O7fiqQf3NXht1lhdmch24HcQ+N2unau3r7Y1xCas+sbN27M9u3beeqpp7BYLEyaNIlLly7lfbB/CLQaLqGw7OGm5FhY+SwsnyydOvaghL+/611wfeah+XD8d1lNXjsMq57V9sNlR/3ecN8P0PkZZwUzvxBHXgVkYs8Mx5pTxfHOGygXTtakqtokT1aSaPWwfaBXZMLs8WbJtsddBFaE4Wsgop09pVJOvtP6d7p+jXOb4Of7RSkrexnVjdMFllHFxMQwaZIsJCdMmED//v2L+2m8g5CaMrnlnOCvHZXd55+TYOl42fmdXQ+/Di34ehvflHIjazqcWSdSn56Aokhk8f6fIDJHmwIqOcYgxSD/zwzte6t/+wQ6T6K+5fNWUfQmerxpd9NT5PduNaJk2+MuqrWTErjQevK7GgOhegcIcyMldmi+2Jave014W5n9+0geER4vwiPLLT8/Pz766CN+/fVXLl68SGJiItWquaiDrqoiEJF4ThZWajaTm7R4WSXlt2LNSHYmLpg8bNJhyZDOlb2DBVWVmslVz0pOvvf7Yt8KMuHX7+PZNmViyCKJaqTGQ69pUD7C+XWzSRYfBi/tCI3+why3mr3nuqU1qreHsTsg/rTcn9Xau65WduOsLFLNqUJCM/jJvaxaZdFQgNlFYmIiNpuNatWq8fHHbkpjljakXIevOwgHRWcka/ekWiXKVRBMic4+7MUpa3MFZpPkTbNvQOp0hw4TZfcc1hDaPyk1zpm+DN7o30Z/eGCJLJD0PmLNmjMnn5FiN5ry0o66fDWYcLJs9+8m/eVx5YDcWzU6uk4gjF4lPB1zKpxa4ZiHFB2EeMlKOB9ofgck71vIR9O/5LypPBcvikCMW+pbpkQpobBlm9yN9oG0+eCCb9rmg8WT++YlmXi7v1GET+Ai1r8hOwudQawjG/YVZnxGsqz+Ww5zHDvqLwntV2wEbcd6rk3ZUakJjNud92tbPoDVL8jAcPcX4vkMssBKvyklgZ7yKi+rA0B2VKgrD3dw7bBj92UxyY6wTk9h0BZURmVOk1wnEBRUsqVWNpvKioOXiU9Op1eLqlQuX4RQ+bUjZEWYbGZZ4PgEySTf+bmCz731eSHFWTMkYuYpHo/NJjnvo4vE32L4GqltP/i9TOTdXnWWaPYLkTB+7W7QdKBn2pQTdXvKpJoTqgqLR0pbDf5SjVLrNnnNZhPtCt/yniPq/R36d3ik++fE7MpmXZ4m94KiB59yBWvWm25KP9CKkJkHNJ3k1d2z6Hf/WNafcYSrO3fuLGI4145JKUn1DjIB5Qe/YOlQN04DClSob883+Thu1oLOfeyQnBsU4bkSq5sx8NfbshCxWSS/Wvd2YdmrqpTEPX7YccNXbS2P0oD0JJngM4V8/nhUQukZKTDnNgmlBkUIO1YrF7p/Cizpcp/mNYBWay+rep1BdlgtHijckObsBiFxXs0o+Dgv4b1lR1m27xJWm8q3m87wy1O3Uc5P7vGDFxI4dz2FDvUrUjGogLKfys3t34/de7xRP2j5sNxzhelxhzUQy9nE8xIa9lTd/elVEnZXrRI9XDpeooKJ56XtRxfBA4sdxzfoI4/SgIvbJTxss8iEvmQMPHlM6rVn3yo55oh28PAabQi+/xSoqiwu87vn6t0h3BJLuhwT9Sg0H1TwNXfPhGVPAqpdFXOq5s0GrYl3h37ER+eY4Ns3rcXq1avRxeyEeT2QFbwqK+MaHfK5iCITzPZPZVC85Un39L71RtkxexQ5xF1UmxBhMifOpBgpESysfK40Yc9MySPZzFKnuvEt6PtFSbfKs7i0S4iSdW8vnglQRqownS9uFb7ByI25F0iBlWDcXjj8s5DMmg8u/Lp/PG736Janx44dIzk5mXLliqjJUEysP3IVk1n6t9mqcuJKEm1qV2Dp3ku894fs0I16hR8e70yl/Hb5ARVgzE7JpwdVlcHQnZSRT4DmxKRcyM6pAdmZ3bzgyL2f/CP3OaUdq/8r5Z+qDa7uF0nuzAje3xGqCqdXyyKtYd/imQAlXpQNUOJ5qNEZHlqRe4EU0RZG/iVOmxFRUO/2wtu37EnhlwBs/VAmeg8Iwmkbk63VhcXD/HnUXtq748g5Bg4cyK5fP+TC9VQ7ESFVwtoFISAMur8G3V5xb4L3FspXk7yczii7sntmQqWmjnCszlB6d8G+QaK6pTPK4+4vSp60UxI48D3M7Sq7tOlNpTa1qNg3Vxjfqk2Ebda9kvdxobXh1ueEfe1KuNS+a6gRDGH2iq42bdpw/XrJGBY1rRaMUS9Dhs2mUjNMBs6FO89jMtswma1YrCo7TscVfKGw+sIT6fCU9zgh7qDeHVCrm/QP32C48zOJ0GSyxit6eJFRHFS/BZreZ9ffKCdjEzgpJP8jsPJZIcEteQRmtHOWlHUXa6dIBYVqE/Ga/d/kfVxEG7jthcIn+EzkrEBQPDMOazvJd5mCf8+X+XxyfxZ98hwVKlTgzz//pN3E+dT8CO79GSw6fwnZlXXcPhWej4cXEmRX9tAKaDEUGg+QnVxpto/s9DT8N1FCdhXqS66u7VhZqCh62Wl2ebmkW+lZbP9UFpwZyRJiO7Wi6NdSrTgIZGpuad+i4p5ZEFCJcr46Nr5zHyBy0b/+qlGttZt4/b5I7m1fgx5Nq/DpiKissHz9KkH46GUWUVGpFVaK731XoNPD0N/h2Vh47jrUvk12aU0GiGDJQytLuoX5Q1FgwFx49hoMXuSo97/9Ham4UfRS9tviwRJtpsex52vZVGYkSxQm9lDRr2WzZKvqUp35YkWFosDA74Q3oTOKGqQGFtR5QVvinU4Pt/0XgP5A1IAnmTBhAgcOHCA6OpqFR2GVz0DubPOIpm9bYsguBlGuinQud5AXe9dbWPWc6IoriuxaHlwiRL2MFLsK29986V+5OVzZZw+XqZLvLSpajZBB5foxUQHr/ro2bazaCp6LBZuVLbPnAFKKExJSRB31YiLQ18DEPrl3sZPubIxOUThx5Sb3ta9J8xol0z7N4Z/tc1RpDoPdWFypqiwevS3NCrJo//EeuLJXdp+dnpF78umL0r+LKsFdllChnt3wyyrfQXEiq93fFJlm0w1JBbd8WJs2NukPU1LkXvEU0RkPGtQA6HQ6FEWhU6dO1K9fn6OwLU0AACAASURBVBUrVpBc7z8e/UBlAulJ4kN/ZY/spEduLFpO+MQyEeCo2lY6sqvlMjYb7PzCIbd5epWEq8tH/DMGAIA+H0kJ29X94j1Qs3PRr+UbJMJOqXGSXtI4/XEl9hrjx4ti3KhRoxg40EsMbhfh72PghXualXQzSg/iT0sqKCkGaneHocvcT0uoqhj8nF4Dje+Blg+5fm7ccdEVyRTD2vK+TPKK8s/p30N+E1JxyjXo8VbxODcV6sLkS5B2Q1LJWm6AFMXjGyqPTvKPP/44ixcLC7VOnZKtFSxV2PWlCPyoNqkE2Ph/cNcnhZ+XHZd2woL7pSOfXCahKVcFZnQ62XGmXrM/10tlwj8JvuVgwBzXj7da7Oz4fBaoiiKCOR7AjRs3sFqtVKlShVmzyqhx0T8Jq56VCV6168sf+klEv9zB3jmwcrK97nqZlL1lV94rCP5hzqJhZcnKVisEVxejJ1dhNUuOPL8JV6f3WP/2NDTdUqekW3j6uz30nraWUTO2UrNVl6zXqlbNX+zjHwdbjhxuUXTlY3Y7OrI5Vcqt3MGw5VAlUgQ9hvxWejgEqip1/HO7w19TJepQ0tjyPvyfP7wdCEcWllgzQkNLloR6OSGNkV9tpfe0tUz6bhcbj8WiFqRA+U+Fzeqcw1WL0L/Pb3LsxM2pcGGb6+eWqwz3/STqbVXbujfZeRqWdHEnnNsDDv5U0q2R32nRCHjLD96tKD4jfzNoupOftf4UO09fx2xVSbxk5sLqzVmvJSUlaflWZRtR44WheSNajCtyOpmlxolbW+XmzrX+0avg8AJh0NbuJjtLRS95fVdKsrIjog08ur/YH0VzHPwB1r0sA9ulHRJxiBrn3TZkpELyFSEgpifCmikOTYRFDwkB6+/OWcgDbyw8yLGYm6jA1pNx7D5zg8dub8CQjrVLummlC7dPEytWUwJUbgHNc2jZJ16QnX54a0cYX1Vh/7cyuTcZIO5nh+eLcJLBDxre5V4bGt8jj9KGVc/D7hlSjnhpu5Sc5ldO7SmkJUi/Dq4J5zaKroBqk3K738fkLyJWRqHpJH/tZjpmq2Nlb8lIz/q/1eplF7TSDP8QEctJixdLw+wh4Cv7YfZtMono/WD8HiGNXNgGP/W3lyB+Lyppj2wVrf7KzVwP5ZV2XNnnvIO57OWV9dWDMKeLCF8E14IHlzq/nrOG2guIjo72+nvmhbjkdCcLjwyLjVUHr/w7yedEpcbwzGVR7/QPdV4QHlkoctM6vYh+PbJdyHl7voblEx39e+gyufcubJG8fnZL0rKMmJ0OvQEQ1rs3J/njv9tlxlWo20tkibP/PlpVxpQiaBquH9q5Nv5GB+kopJajVK5CBSkPuHy5GPXIfycoipA4cuZ4t7wnSlXpN8XuMLMm88JmR+lGphFGlRYSBfi7TPAATe6Vsh+DPxgCoPkD3n3/da/I4GxOhYSzQkrs9KxdE8EH7vrcq7v4NWvWMHiwRGmaNy/Z0tMx3evjo3fcr74GhVa1SqGORWmATi8lUTnvlbVTZJLLSBbBrDNr5O+nljsWt5Z02dHX6Q5dpvx9JniANo84+rdiyN991FP4c4J8/xaT2Msa/aFOD9D5iK7A31AATNOdfOOIYH6ZeBtbT1xj04lr/L58e9ZrCQliFvPUU09Rv3597rrLzfDTPwXlwkVgx2qXSM10j6vVVYgh1gzR8m9UjFDchrdEd98nCB74rXjMcq1RowOM3iqDXPUOBVsLewLGQEmBqHainTEAer5pdxs0eJ278O6775KamkqnTp2YOXOmV987J3q1qEqz6sGsO3KV/edu0CiiPA/f5qaG/z8d5cLh+gnA5uwO2egex0Sv95Hde1Fgs4oP+uGfJRQ+fJXdHa6UoPVIMWy5flTMfEJqeff9DdmV6lRJhz7wmxgn+QZ5Tiq5BKG4Q5yJiopSd+3a5fLxZ86cYfny5aSmptKxY0c6d5bJpF27duzYscPtxjrhxDIJa1VrLyGXv0tZXnqShJMubRc5xntmOUrjzm2CY4tFDjRyOJQrggRi3Cn4ItIRMitfA54+r137yzpuxsC3vUTit1E/uH+Ba6WJGSkSAQiq6vpOPy1B7mGfciKklMf7dO/enfXr17NmzRp69OjBsn2XmL7qBEH+Rv7v/pbUq5K/P4OiKLtVVY1yrTHu92+PQVUlfH1mveSnm91X0i3SDgnnYP694mLYYZIzH+fIQjj/l+Txm91fNO+No4tkkjenyCK1wV2li3hX0ojZDT/0Fd5Tp2fh9v9z7by0G7KAcodhn3BOfo/QujKWFDYuqKrwf/Z8LaqKg34p0Mve1f7t0RK6OnXq8OijjwLw/PPPZ/39iSeeKN6FL2x1lI8dWyz/2kV4NIXNBntnS91pi6GFG2hoAd8gGLYs79eqtYMVk8REZt0rMOhX940xLCbnm81iyvs4q0XIf+XCPabEVCpRPkL4Eu7g9BoRH7FZRQf/gd8Kr5W3mmFme1HjUnRwbAkMyV9sRVEUYhNNTPv9CBkWG3HJGbzw0z4WPCWmTfHJ6VxNNFGvShA+hjK+4N09U+5zcyocXyx9on5v7d8nIxV2fCYEuXaPSdmVpxFSC8bls5Cq0QmWPQEZs6R8bvRW93X6zdny3apNFp/5HRcfLbv80lJZ4w1EtBW+hDvYPh1WPi3/d9VIJukKfNFSNlM6I9z2Ym6CdU5Er4Ltn8gC7eINuRcG/QxAzI00kk1m6lcJQqdzL13otdHgwQcfzLLKnDFjRvEudmmno+zMnCq5FU9g7Uuw/CnJk8++VUQuShLRq0RVLdMDYPXzhZ+TE5WbQaP+Dk/zO/OozzebZAKa2R4+rAln1hW/7Tlx/QR8Hgn/qwI7phfvWqnxYuUbvcq5PthbWPaE/B7WdDi3Ac79Vfg5N86IEZDFZJ/MlhR6SmKaGV22BVpCquhx7zkbz8CP/uLxuTt5cPpmUkwayG6WJM6uz0a+TJNFvScwfwCsfxU2vwszopwnyJLA3lmiXZGRJFGhze+6f40mA2QXaPCX2vpeeVzj5iX4qA7M6gQf1pLJXmucWQcf1oYPasKpYsoA3zgLe2aLoZS3YbPJBG/NkMfWDyQKUBjOb3KcY06RzWJhSInN9r4WSLoEwKKd5xny2SbGzdrBpO92Y7O5N8Z5bZJv2bIl27ZJrefmzZvZs6cYrOna3ew7JUVypk09FM47sdQx2Cg6CaGXJPxCHJOYohNmvrtQFLj3O3jyJEy+LGYpOXFyGcSftC8mUkQCV2v8MliYtSmxYiZx7VjRrpOeBF+2FMe2nwbA+je0bacrMGSTLlVV1/J65avliKLk3nVduHCBTZs2ZT2vV7kczaoH4++jx9egY3S3egDMWHsKk9lKaoaV60kmNhy7WpxPU/JoMsCuuW63o613h2fe59xG+Q1Uq/TzGyW8iPcLlV0fiJtmUTzGjf4wZgc8fgQmx0C1PKK5u76C1OuymEi7IboUWsJmhR/6SUri5gWpCiqqQUxmevHPCaIieOw3bdtaGBQlt5FMzud5oXw15yqClGuFn9OoHwRWFq6UMQC6vgrAl2tOkWGxkWa2sv98AqeuuleO7tFwfU40adKEzp07s3nzZjp27MimTZto166d+xcKjxQp2OO/Q3gr0QD2BOrdIatcS6oMBBEutNWTevQ1O0tYcefnEFwD/lNE9TNFyR2aPL0GTvwh7+EbXPzFRGFIiSVLEEinF59rS7oMtME1XQ8hXtohlQhm+wS5ZyZ0f1X79haE/8yG7/rICr/Vw0IYLAzGAPkdMr9nnRHS4rmWmMratWs5f/48U6dOxWKxUL16ddq1a4dOp/DJ8CiOxiQS5GekVkX5jkIDfdDrwGoDBYXggFLo7OYOmt0vA93FbdIHPcUur95RStRsZumzIYUQ1DytR99mtFRzZNqVdnmpaNfR6cTxMBOqKtayMbugyUBRt9QbwWIVHojWTp9Ws/MC1maR59YMmfRD67ku83vid4mQWe2LhN0zvFtNpCgw8HtYOFQ+R5+PXVMH9QuVEmir/XuwuVCa5xcMjx0Sz4HgWlljdJC/gcQ0Od+mqpTzM7r1Ebw6ySuKQpUqoiGckZHB3r17izbJg+RWItpq2Lo80OsdmXCuHRVWaFj9/I81m+C7O+H8RihfXRYhWjNHk6+I1npwTRkAKtTT5rpnN0pO2ZwKu7+SMrHWoyR8GFwL+n2lzftkR4+3ZPet04voT0hd+LSRTPY6I4zeDJWaFH6d0LqO0kKdUZz0vI2qreHZqxLac5UAqijQaqQIngBUbcvJq2l06uxsJXv33Xcze/bsLA95vU6heXVnA5hn7mpCbKKJc9dTuLt1BJ0alE35TSc06OM+38RdPLBEUnGmG2Id7ROQ/7FJl0W/IuGMLPYfXqN9Lvv6MRHJCWskOhhaSU3vmC6pvcz+/dBKYe+fXS8L0luLkPYrCEY/2YzstW9CWgyVctQ5XaSvlqsCY3e5trio2MRRVWTwhyottW2rK2jSH15Mlv+7unkLayCb0WtHZJHVdoxr5/kE5Kp2mjq4FS/O309implHe9YnItQ/n5PzhkfZ9TmRuSu5etURTnz55Zd5440SCLFqjT2zJKRkTpXdb9P74X6NZRvndJNcj2qVneC4vVCxYfGvu+FNWPcqWTvrZoPg/vnFv25hiD8tYcOqbWD7x7DmRfuKXYHIoTDw24LPt9lk1Xt5j+Tkg2vCXZ+6Fua0WoS8eG6D/FYdnnIv+mKyRw+CiiHXrKpwZi1qRipJVTrxzPP/ZebMmfj6+jJw4EB69OjB6NGjUYoYFSqz7PrSiN/HC+tZtUoKoedU6DhRu+urKvyvsvQHkIqL565rU9L1bW+JDoCU594+Tdu254erdn+OKpHw8/1w1E4sNfhBr//BLYUQsM0mEcc6s0aitjU6imWuK1EAUyIsnyRpx07Puq/+l3LdoWVSVFjS5Xv3CYLaXTWP7pYKdn2uNzMYGDx4MJ984iB7ffLJJ7zyyisYDF5tivZQbTjJgXlCGe3GaYcOtqKX0JcWk3zNW2WVbEmVxUM9DzCZ80KFuvIAGdQyV+w6g6QMCoLNJqUw5zbKd93jTeg02fX33vq+LCzMqaIyGFJLcsGu4Ohi+PUBGZgbD4D7fihaB1YUjmVUY9iwYeze7ZDS/Oijj7Jc5/5FKUH2/qyq2vdvm0UUMDNhzZA0lKEIZbI5Ub+PQwtfpxcWvzdQpYXj/37B0q9tdv2JwsoD05PhqzYSvVSt7lcS/fYInFgi3+PlPTB2t+uVCpk6Iiji3lfUSIfBV/LsJQyv1tpYLBbmzHF2/ho1alTZn+BBQlKVm9oFbCpCTxfrL91Bp8kyCfsEScirekdtrlunu3hltx0H/WZKasLbaDVSys/0vhL+LsyTPe647MLNKUJwWe+mh/vlPdkUxtIg1o2yuWVP2HOM6ZIzvLIv30OTkpIYO3YsERERVK1a1ekRHh5OkyZNsib4kJAQxo0bx8iRJfD9/4uC0eUlu1CVj4Ri2zyi7fX1RhlDfMrJo05PGUe0QIeJcNdn0Ha8SOVWb6/Ndd1Bz6kSajf4Se1+i6EFH3/yD0i+LORAc6r4WbiDq/sceXydQcqBXUFGKmx43c6MT5cKK3M+ZcZlBF7fyU+bNo3HH38862+zZs3mrbfeIiCggHxYWYBPgLBa0+KFBa+xpzggIeUanSVvV7dnwTlEd+GNHGhBMPhIfbmr8Atx3k25Sx5qPUqYupkDgSv5/0xkD6GqNtD7cvXqVV588UVq1arFhAkTePvtt9m+fTtHjhxxyrHnhWHDhjF9+nTKly/v3mcoxTgfl8Lp2GRa1AghrNzfQEUspCZMOic19f55yNVqgQHz4MwIIWnVvV2791AUWbiXxOI9E+Uq568PkBcCKmUj/+qhnJtpsbZjYe3L0r8tJqhQAJ8qO3R6eT8sjvf2xFjuRXg1J5+JkxdiGfnZWja/K7rkK3cco1e7RsW+7r/4h2H/t1J+5xcM9813T6zIkg7TKkiKAmRQefaqSwOrem4zP77Qm3UnUqFKS8yVW7J06VLi4vKun42MjOSLL76gTp3c7G1fX98sXwetUVI5+d1n4pj8/R70OgVFUfhmfCe3yUL/4h8OVYU1LwlRsEIDGLLQPf5L3EmY3hxsGYAeat8GI1zU+9j/Lfw+FlCkgqmFl/0zXESpzMmDsOr/98U8Luw6kvW3JXsuajfJWzLEwrV89aLJQuaHi9uFgW5KkNBd13zCR1YLrH9N5ClbDIWosdq1oSSRdFkEW0LqQH0P1S27i5YPyaMoSL8p+vSZSIuTfKHeXp5iyRAzkYvboNUIKW+y47Mle5jwU2ZN+z77Q/zeMzIySElJoUmTJrz55ptERETQtm1bfHzKeFmbG5i/7Rwms0RZDHqFdUeuMLSzRvrpGSmQeF6qKrTUGT/4IywZI4u8/8zJX0rXlCh+6AlnoPPzpacvFBfXjgrbPqJd3rX13oaiiOSsq7KzOZF4Xu6PjAzACvGnnF9PjRdVxcTzcNsUqHe747WWD0HkMEc7yji8OsmfPHmSBx54wIlkVK5aIxrXrqbNG6QliHJV8hUJsYzcCOEalVz8+qBDkeivt6HJfVA5jxDvpmmw7UPJI8Xslnr2Bndq04aSQsp1+LyFo3Kg26vQ+Vlt3yM9WULffl4KWQdUFPep83axmcb9HRM8SF5ux3TJ11/eI2YfdXsCEBiYu3Tq9ddfZ8qUKSQnJ7Nu3TruuOOOsp+CKiJqhQXiY4gjw2LDoNNRVatd/LVjotJmM0sd8rjdEKgBMc1sgsUjJQcLYgXbuH/engWLHoZTf0oY+OI2ePSggzxaVnF5nyh6qjaZ1AYv1F5GOC1BJl2jlyI61TtCoJRro1pFjjY7fn1AVPlsZtHaePyopGQy8TeY3DPhMeKdqqpER0dz7Ngx0tLS+Ouvv2jdujW7d++mevXq9Bj4MC3uGc9T787lkR4NtHnTgz9IvtqcIju19a9pc11wkLRAcjwLh+btPRyzy3GsNV3KSAq9tkmIX+nJeb+uqsLo3jFdNJG9jfN/2XNbafLd7imiCE9+2Pg2TAuGd0JhVTYma9xJ6YiekBtVFCEh3b8ABi+CAd84vx6zy6FYZbM6EfPq1cutT1CzZk30ej3BwcH079//HzvBA4zuXp/bm4VTMyyAoZ1q071JFW0uvGmaRNIykiHlKuydU/g5rkC1OvM7rOmi4ZAXrhSB0GVKlPsnP9U3S4aUgO7+Wohf3kam/4clTf7d/03h57iDn++Hd8Pg7SA4mK2sOGYPnN8slTJawycAxu+Vfj1iPXSc5Pz61YMOgRqdQaK/f1N4ZCd/8eJFhg0bxoYNGwCoXLkyLVu2JCUlhaioKFatWkVISEghVykCfMvLThNcK8NyB3d+Iu5wmXVycSdEK71hDsvc1iNFtUpVpS0N+xZ83aQrMKOtyLPqDPDIttxlcWumiHGBahXZ1iePg78Hvr/8ULGxo3RP7yt17a7i9FpYMEgWRr3fh6hxzq9bzRIWz8Tmd+HWF+Dkn7DkEflOgqrCuD3ai4/o9PmTDduMsWsSqPbjHNGYFStW5Dp81KhRnDp1yqkcVFGUIte4l2X4GfW8MrBF4Qe6feEQexmWWQhRWqXjfALlntv4puNv++dJSi6nMmSrkbDlf7IoMPgVrm4YsxvmdgdUYeeP3ZVb5ObHfjLZqSrs+gLG7PSuq2aVFlK1Y06RfyPcCNfvmgErnpbv4v6foW4P59fPbYIjvzieL35YpLRXPgc7p8sYWaurOOVp3Vd8y+WvhtpqhIypqFLN4M5nLmNwi3jXpEUrdcGf63MpbmXHn3/+yYABA0hPT8fX15f0dAmBhYeHc+XKFebPn8+gQYOK3fA8YbXIDvvYb2LEMvTPAq363MbMWyS0A3JT3/qC5OVyylxe2CYiLXV6QMVCuAYb3pLQsM0CKJL7vSeHb/gHNcTMBGQhM+gXqNdLk4/kMo4vFXOGsEZwx/+kA7mCdypKvhtkgfD0BecQa3IsvJdjp9fyYRHOyLBHNnyCYMC3UjYXe0i+o9pdi/+ZCsOFrXD1gDCds6kLJicn8+yzz7JunRB5zGYzp0/n1j2vU6cOixcvJjIy0vNtzQPuEu8at2il/rl2E3Uqufjbehup8fDD3XB5r8jdDvrFdXlUVzA1WCKAIOqJ/efJhJR98lFVWYDevCjyquUKiVJ8dzecsrtKGgOg94fOPB2rBd70IWvzoPcVFn9h19USqipufEd+gdo9oOtLrjHKU67J2JSZ5vCvAM/nIJ/u/w4WZefNKNB8MByaT9ZnNvjBmF0SQUiLg07PuO++5y5UVTw6ki6LPkZxRG9KCB4h3l2KT+WJubu4r30Nnrgj9+SlqiqPPvpo1sTu4+OT9X/NcWGbEEVqdoZaYreJ3uBZpbb+8+D7O4WsYbXApv+Jic0j251X3jU6yMMVZBeJ0Btlt5ITVdsIH8CaIceFaSCA4y4a9ZWHq8hkx2YX+FCU3KH3gIoQVC3LcQm9Lxz60RESBYkiHPlFJn5LGhz5FcbuFF0CT6JGR3nkgM1mw2KxYLEIcS+/3fqZM2d48cUXWbp0qUebqRVi4lMZ8eVWXurfnF4tiqHkpwWOL4Vrh6HRPY7yxoAK8IiHHOlAFg0LBktKQFHg9zFwZrWzR4Si5I7eFQT/UEf/RpFFenboDSLElHhe+oxvkEyW3oSiwC1PysNVmE1CVLRmG9/zSqs1uMtZw13vA4d+xlk5TIE/xssGymqWfj7xnGf5OYoCDe/23PVLEdyKCdlUMJmtLNh+Ps/XFUXh5ZdfpnXr1oAIgQBUrVo1azczbdo04uPj8zw/F879BTPaS7jr+gnnv3/TU+ogv+sDJ5e78zGKjkqNYeIZCRWqFrCkSK4t4UzRr9l2rOwUDf5QrX3ephQDvpW67vp9JI+stSa+J3B8iSjKZXZmRS/VBtnJLSCLo8cPi1xlr/eEmJM5wSt6KW3r+bZoQGfmyHU6uLybksIbb7zB119/TXR0dNYjPzz99NP5vqYlTscm8+Wak/yx7xLuROeyw6ZCusXGvL+85Ma2/zvx3J5/r7N9547P4ZchIkQyo504kXkD9XqJ1kXmPWhOkTYWB3e8J7KuBn/ZMTa7P/cxI9aLtHLj/jDyL2cCaGnFX1MhOlvaSjHkbWsbUAGeOArdXhdzF9UGZMvBh9SWxdXlvfZ+rwoHpjhjqta4flx4SFcOlFgTdp+J58vVJ9ly0gU3uxxwOyevAGFB+ZeujB49mqFDh3Lx4sWsv9WoUYNdu3axZcsW9u7dy5AhQ1i5shCP4fRk+P4ue8hWge96ywQLMoFk+U1b4OhC7wq5BNeChNNyw+r0Yg9YVBh8JR+VExmpMpGF1BaGft8viv4eJYGblxx5fJCIy3++zvtYv2C41W5ne/0oHPpJdj7+FWDCScmZpidJuN6cKjueGp3zvpYXcPbsWQCeffZZBg8bwcRvd5NhkYFrWOfa3NlKqkUiIiK8QsC7nJDG6JnbMGVY8TXquHA9hfG3Fy3aY9ApVAv1Amnw6kFYOk5+z2tHwTbKIYZ08HuHq6DeB86uK9gcSksEVnbwehRd8RfUQeFSBZATqXGyQajcTN5Da58LTyPxrMNpTtEJsS0/LfrQ2tDtFem3B76Vz60oEN4aRturW+r1glMrhG/hEyi18aUBl/eKMVHmZuXBP6BON682YfeZeJ7+bjfpFht+23S8dm8k3dwgs7q1k/cx6GhSrTzvDy2YeOXn50f9+vWzHr6+vnTu3JnVq1cDsGrVqjxzmE5IvS4rOgBUR04ahOxitA9ExgDvaTFn4qEVULeXTDTDVmhbjw9SbvJ5M9Fm/7Sx3PxlDU0Ggk95CU8a/OX/C4bA1UMFn9fvK+g3Q3YF4/dJ+G52F9g0VRzmbntRyImloGypffv2JOorYAypilI+HKV8OFuu6LPu++JM8KYMK5tPXOP45ZuFHnv4YqK41gIms40Nx2KL9J5GvY6ouhV44Z5mRTrfLdywR8RABvbrxxyv1ezi6N8gk4G34Fcehi2XMaXeHdLXtcb14/BxPdHd+Liec5SyrKD9k2AMFHKzMVA+05IxkHw1/3MURaIWvT8QbsLwVVJB82ljiF4tadeur4rOvJZqnsXBkV9lwWlOlce+uZpc9kZKBhuPxXIhLqXQY3dEXyfdvokwmW1sdLN/u7WTr1u5HLPHFl0vPSoqisjISA4cOEDr1q3ZunUrTZvmk1cNrika5lcPyAqw+RDHa03vlbKU40ukI7Z6uMhtykLyVblmWIPCWZ4V6sJDHkwRnFgqpJbM3cyGN7SvW/U0gsLhyWNwaSesek5CezaL/DvpQv7EPZ0eIh90PF8+SYSIbBkO0l2V5t75DC6gRlgANnt43KjX0SC8+As+k9nK8C+3cD0pHZuq8tjtDRnUIf8dZcOqQdhs0gZfg46oOkUjEdWrUo6PHvISy7h2V3t+2m720iGbK1qPN2WQv7wHWo/WRpwl4Ryg5E4X5YWancXq2FPY9ZWd4KdKm3Z/JZUnZQnVouCJY1JSuGi4eDjo9KId8FgBZcM+gdAum/nS4pH2MkRVKgy6vQblIzzdetdRqam98sBu3qWB7srVxDSGfb4Fm6pitam892Abourm32db1gzFzygCU35GHW1ru8fZ8JoYjqqqfLk2mnifqsABbt68ya5du7Im+ZSUlCyRkaz/P7xOhCeMAZK3zo42o+ShBfZ/JyQbRSeM+CG/ebeEJSeyM2t1BiGmuYJzm6RExWqWHXFJi/D4h4oi2I/3OGpSbRZxz3NVKz41zvlcU6JHmhobG+tEGK1SJXc4LD09ndjYWE6ccOy8GoSX5+X+zflx2znqVCzHxDuLzwo+dCGB60nppGZIJOu7zWcLnORrhgXyyfAoluy+SK1KgTzQsXax2+AuTBlW/u+3Qxy4kED3plWYcEcjdLoCFst+wfDYISk3tWZUyAAAIABJREFUDa7lbJqiN+SvKFkUrHwOdnwq/+/4DPR8s+DjPY2gqpKms5jk33IuTmr7voHVLwg59/75zi5vJYHg6tInrelILt3i8E93tRzOdAMHb0cnpMfShBYPyHh1dJHMQbdMKPYl1x25islsxWyVz/3j1nMFTvKdGlbilQEt+Ot4LFF1wrirlXuLII9O8jfTzChAkL+RdUeu8vOWM1w5vCXr9dGjR3PkyBHOnj3Lzz//zMiRIwkMDGT69On07t2bX3/9Ff/G//FkEwUrn3Hkl86sk9VphBu14Fqj7u1iRrNnltSo3/VZ4eeoqpQXZZYAzb9Xylm8pTBVEBrcDdHLJf0SUBFCc4vJ5ItbX5CIjWqTnZ8WUZtsSEhIYNy4cfz8889Of+/bty+zZ8+mUiUp9/v9998ZNWqUk9lMrVoy8fZsXpWezbVjo1cu74fVHh3QKRARUvhvGFkzlMiabpr0FBPxyekE+Bjw89Eze0M0G47FkmGxsXjXRRpHlKdPZCGDkX9I3kQ0LZGeLAqUNruE8eZp0GVK7rJXb+KWCVI/f3adbCpcYbUnXhQOg8Uk7mzzBwpfpaQRXEMkxBPPAwrU6uJevXuv/8HP98kEX6mpuO+VJiiKWM0W1W42D4SH+KPX6TBbrfjoFWpUKDw10aNZOD2ahRfp/dye5BNSMpi57hTJ6RZGdqlL7Xxqauf9dZqZ64QV+2jPBuh1CjZFocH9L3FuxZdguklqYhzvvPNO1jmzZ8/O+v+ff/7JggULGD58uLtNdB++QaKgBfbJROMcO0g9ZnIs7J0l9ZkBFSU10HasowQwE4oiVrXu2NXarKLrnQnVag8xlYJJ/v6fpAY2PUl0od2pba7cFCadh4Sz8n0V8/MsXLiQiRMnZk3WaWmOsp9q1aqhKAqXLl1i6dKlVK5cGX9/f6xWKxkZwvgvX748VapU4amnnqJdu3bFakt+qFkxkP/2a8asDdFUKe/nGWGZfHDuegpzN0Tj72NgTI/6hAbm/q1UVeXlXw6w4ehVdIrC1CGtuHQjLYt8aLbaiE0sJfacemO2Ejak/l3ngb1NfLQssDe+JWSt4JpS6trpmdziVgZf94l2afEODgMIZ6k0QKeXEuL984R74+4ivOFdoguQfFWie2Xc8c0VdG1cmQc71WLlwcs0rRbMuJ6eJZW67ULXYsynnLyShFVVKedrYOqQVtSsEEjlYMfKOC3DQq+pa7HY84QGncL8J29l1IxtWGySh/hgWBtij+3gkUceoXr16jzzzDO88cYbpKamYjQaOXbsGJ9++ilPPJEPY1NLxOyGnwZIRyquLvvFHbDzcxFP6fycdOiDP8Jvo2QBYbM4S2gaA0QFyx2r0/ywYjLs+hJQhPg2UGN5yjKOpKQkwsPDSU11lg7t1KkT8+bNo3596WwXLlxgxIgRrF27NuuYgIAAXn/9dZ5++ml0JZnKcQPuiuG0bRulVrz/XW6azOgVhVoVA3muX1NqVwwkOMAx2R+5lMhjc3ZiMks6ITzYjzfvb8mT83ah1ynoFJhXmpznjiwU9cRM85nG9xT9Wsd+g8MLZMfa1m5os/q/sO0ju8y16ty//UJlEivuxsFmg297SS25zSplpR0nFn7ev/jbwmMudCevJGVN3skmC898vwcVmDq4FZ0aSGhTpyhOERtFgSrBfvw84VaOxtykZligDAC1+3D+/PmsQfPee+8F4Mknn+TYsWN4DRFt4em8a//dQsJ5mNdDCHMGf2EQ958teuyWfHY2ik4WGVpM8r3fF7U4m0VIi6UNqgppN+wCQJ5dsa9cuZJ58+ZhNpvp2LEjjz/+OG+//XbWIvLGjRtZIjY5WfA1atRgzZo1pKWlZdWcG41GjMYyUL9cDJitNtItVlQVLKpKdGwyT3+3B4BZY27JitoZ9QrZxUyMeh0taoTw0xOdOXMtmSYRwYTkEQEoMTQdKI/i4vRaMaoyp8KxRdLP2oyGze85Oxpmh80i40B4MVUPdTp4aKV4KviFFK6kWRKw2SSn7h/6tzJ4Ketwe5LvUL8iO8/EYbGq2GxqlqXkzLWnsiZ5X6Oe5/o25d2lRwCFF//TDINeR3CADx3qV3S6XvZdUZnV+Y7ZY3emsjgmL0uaKPKBdMqbFxzH63zsPsfYa741LAHMazC5uAOO/y48gyYDtHsvEP3+xPPQsF/BEsIZqTC3G1zZL4PAqE0eq33eunUrvXs7qhEWLFjAkiVLWL9+PQBTp07N00kuJ/z9S8lO1EswGnSElfMl9qYJmwpWm0pKugUFWLDjPM/eLSTZBuHlGRBVg/nbzhHoa8hKJ4SH+BPuAn+gzOHUCplck2LAYld4M6fCmTXixWDwEb2OTCgGmfQVvbDJwzSq+dbpofotuf9+4g9RAG3QRyoDtILNKhokFhM0va/gVFnCeZjdWVKSlRqLqI+3HCX/RYFwe5KfOrgVf+y7xIkrN1m2NwaTxYZeBxVzCOT0a1Odu+2iIAWybMs6Lu+FObdJR9Bnfgc6IfY0tpsj3Pcj/NRfpGnbPS4dNeGsMMeb3S+LgG/ukBKx1qOkhEirBc/lfTCvu6MEJKd2dnHw1zTJQaLCmhelpMY/H/LXge/k89kyIPWamNJ4SIJ4x44duf52+LC4yFWoUIHw8HBiY2OpXDnvRcnJKzc5dCGRlrVCqVvZczruRy4lcupKElF1w0pFaFsBZo/twB/7Yjh0IYFNx2PJsKoYDToqlnPu30/1acwTdzRCp5ThxbkrOPCDVN5YTI58vtUqfanxAJl4B/0qVS2qTeq8gyKkLMyaAW0egcQLouCXel14Ni0fKvx9XcXBn2DJaOnfW9+Hh9fkKcVcJPwyRHT6AbZ9LGqA+aWqNrwhvCPVKjXze2fldn4rLTizTvzlG9wF5TWyOc8BVVXZER3HtaR0bmtUySnd5W24PckbDTr6R9VAVVWC/X1YtOsC1SsE8Hy/3AIaHp3crx2Dda+IucHtUz32YxWK06ulM6s22b3X7iauSiG1JHQOompVEBN24XC58VQLbP1QVuNalb+dXe8gHZlTRRdaq0l+z0xHLb/OABe25K8HregcCxdVFbORTKTGyQBYoYEmpYsdO3ZEURQneddWrVqxatUq4uPjGTZsGGFhYcydO5e+fZ31+PecjWfSd7vJvHOnj2hHswIMmYqKDUev8uqvIpOpUxTmje9IjTCNXfaKgOAAHx7sVBuzxcYbiw6y43QcrWuF8kCn2rmO1Xuyf59ZL5NWaF3o8X+uGyJpjSMLHOqaNqtM2gEVZaGe6eXQoA88W4AIzPQWcM0uAvX7OMnnayVNfWyRo32WdBmPtJjkVVV28Zn8gmtHRJAsP52B7Ok31SY7+kzcvCR8hdDaxW9XcbHjc9HtQJU06uNHRNNDY3y9LpoftpxFRWXGWiM/PnErgb5eq1h3QpHfVVEUxvVswLienpMfjI6O5saNG4Co6GWFTy0ZMPtWO+NUB5e2i/1qSSAiSqQ3bRZZ3Te4Gzo/49414qMdOT1LmqyEMyd5q0Ucoq4fFZvLvIxvUq5JKLFS09y619Vvse8+MvLWGygOqrSUjp9pnBNaz55zD8kdiYgcJqv7i9vk+YVNsPNLKb9ZMEiOj4iC4WukTtoVWM2w/nW4uBVaDs9i9rZv354dO3awY8cOtm3bRseOHRk7dixz585l8eLFHDp0iLNnz9KvXz9eeeUVXn/99axLrth/mXSzgzi19vBVj0zyi3ddzEp1GfUKm09cY0jHkp/kM2E06Hjz/uILfxQJN85IOag5VaJjSTEwaEHJtKVWF4heKW0x+ECz+6Cum2VeSdnUOq0Z8nkyJ/n0JLFXNiVAh0l5KzkmnBd570pNcverOj1EPMucKtHD6hrt4hUFQurIb4FNxjj/UNGpyGmVCxLBOPGHGE2pVvGtaHiXLPzXvybHtB4Nd7tQDpyJtARY9aykA299Aep0L/7n2j3DsTFRdFLG2OKB4l83B5bsuUianZiq11k4eimxwFp4T6JklhaFICJC6ms/+ugjPvroI0AESqZMmcKUKVPQp2aqwalyQ8WdFNKHO7tAVYVlT8K+OaIP/+AfRVtp1ukOA76RsFnNzkUTSwitDRcz9QNUuzqXHatfgJ1fgCVVQt7j9znn+E6vFT9qRSeiImN2OEtC1ugoBhAHf5QJP+pR99uXH/rPgeUTZZHSerSYBSXFSOnQ6M3Og4HRTwax30bJb2cxSRWCxeQwnrm8B85tzO1JnR82vCWRD0uqLB7K18g6NyoqiqioKB577DEADh06xCeffMKBA84mEx989AndB4+na5NwFEWhUdUg/Iy6LHWp+hoo2OWFhlWD2HM2nnSLDb1OybcU9R+J68ccZW7WdMmHuwtzmtSSn90gMtgPLClaNOCWp6RvndskFqnuTvAgevhZIi/2/p252/7xHrE0tpqlj046J3n8TOz4HFZOljbUuwMGL3Se6NuOldz/uY1SUVNPw0X88NWw/Cn5LlsOF1tZcwrUvwuGLHTevZePgMiHRIcgM6q5ZzYc/M4RSdwzU6qXsltNF4SFQ0Xu1pYB5zdJOjC4huvtv3JAJvFq7R3fd9U2cn9Z06WdFT1jaVuncjlupGRkVZNFeMMPIh+Uykl+woQJnDhxgiVLlqCqKlarlaSkJF599VXefvttgoKCwGR2mBnpDTDdoVAWGBjICy+8QJ97hzFn42kCfQyM7VHfmfEbvUp0iM2p8qMvHV90qdqm98qjqAit66jl1RmdCS7Rq2QSA+nMMbucJ/k1LzrCdYnnZFXffJDz9Rvc6Rn1O79gmegB/nhCdvWqFeJPysLkthecjw9rgJNvduXmcmwm3NQoOL9/A+PmpbIrBiAV3rtHqhpyQFVV4uLE5UxRFIKDg1GBDMWP2n0n8NrCw4zoksqILvXoH1WDhDQz205dp0ujyvSJ9Izl6iPd6pNusXHoQgJ3tozIRUj9R6Nae+kHel/pF83z2Wmd3SBRrrBG4t6YXeBm+2cS8reaZDe5+X/Q4/W8r1MQdDoRpurwVJE+CiCL77iTgCr3Z/bJ8eJ2h12rNUO4OpWzpT7X/NdRmRO9Usaq7JU4igJtH5GH1git7TANmnkLpNvVJs+ulbbkHFMq55SAjYSjfnaTMQAlG2/JBVzZ5yAo6wzyHbo6ycfshjldJMWi08P9CySycNenkuKNPSQbMg9VIb15XyQfLDvGlcQ0RnSpW6Kcm1I5yZcrV465c+c6/W3NmjU8/PDDXLp0KQ+PejMkOcQhrl+/zqOPPkrAS2+hCwhGAT6vFM6an2dQr55dbS39ZrYcsc0ur6gxLm6HLe+JMEa31/PfSXSYKH7p8acgtA50zGZP2qgf3DgF5lRik6y8MG0hx89+RkBAAJMnT6ZPQEVZ5as2iU7YiW83b95kypQp7Nmzp9BmBgQE8PTTT3PnncVYCGTm3FUAJe8Suaqtod9MqSmu1ATu/FQWBj/0heQrcMtEqOYQmDGZTLzxxhts2LAh16VsNhv79u7GlP1WSE0B8jZ8UBSFUaNG8fHHHxMYGMi6I1d5a/FBUtKtmMxWlu2LYUSXeuh0CqO61mNUVzdU+VzAqlWrmD17Nlu3buXcuXO8+uqrvPbaa07HZGRkMGXKFLZt28auXbswmUxFto0t0wgIg0f3S58oX112qDkRd1JcKs2pMnEmX3F2OUxPdMghW81gctHe2h0cWSiuatU7iOhNfmWhfT6UyhJTgkT7Mgm5IPyds+ulrcYAWfBnh2+wQ8UyU/WxJKDoCn4OkpJLOAfHFjskYCs1k7JDmxnumu4e4z5yGOyYLp/bGCDpPFdx/He7v70KVuDA9zLJ+wRC389dv44b+O2333jppZc4efIkdevW5dVXX+X10YOdjklMTGTixIksXrwYm81G3759+eSTTwgL81wov1RO8nmhZ8+enD17NitHXxCWLVvGk09OICnuEsRdAiDpwhHuvvtu5syZw+LFi3l87GjSLTX4dMVJkjOgbrfmPJ2aqp016M0YmNdTwlt6XwlpP7A472MDwoQAkp4kO9ns4bjub4iwzrVjDJ+6iRXrf8l6afXq1dzZqzvhySEyEITVglM/YFO/Z9WqVcTExLjc3NWrVzNp0iSmTp2Kr68vKSkpvP/++zRq1IhBgwahKApnzpzh448/5uZNZ2e00NBQnhk/mqonl8lOpFJTaDsu7zeKfNDZgMavKUzM7Uh49OhRhgwZkiu8nhP9bu/Ee2N7EtriLv6/vTOPiuLK9/i3GpoG2WQJoIKIGEBwhYgBiWg0KmAMjMvReCRuiTHGBDljlqdORo2PEPPOPJd5ThuNC4nRgehgkCiOMQ6oiaISWQSVTUA2gW7Wppe6748LBQ0NNNItQupzTp9DV9+6VV3Nr3517/39vj/YdO2YRSIRLCzabjCj7cygatF7MDIUwHOEhnVGHXL+/HncvXsXs2bNwsmTmtXOGhsbcejQIfj6+sLf319NjOcPh8WI7kfP5eltCnDKJqCoQ0GZl94Fbh9qeQgQ0aUiXVKYDJxZQfvPTaIPEoFbNbe18wL+XE7vBR1nqpaepo5MJqWFWzqmqS2JA2IXU/ueHd1/AcYh/wccn03Pc8w8WoWzIwxDr0H76zBmDvDxU6rzzf6CphfXPQbGLuzdA4LDJHotW2cVNKUe6pCUlBQsXLgQ7733Hvbu3YvExEQsW7YMVlZWmDNnDtduyZIluH//Pg4dOgSBQICPP/4YoaGhSE5O1tu59VrxLjX1KdbH+oGKyidYvPMUJI1yEJUC6Ud71h52d3fH8uXLNYqeeHl5Yf78+cjIyMDvv/+OpUuXorS0FElJSViyZAldQgBw8+ZNXLp0iTr1uzGwETZjxUSg1vAFnHX8b4SFhfX41CaVSvHtt9+irq6O26ZUKrFtGy3aIRaLUVRUhKioKKhUqq66weTJk7F9+3ZYW3ddtYgQgqSkJERFRUGpVGL8+PEICwvDiRMn8PAhlSUOCQmBp6cnxGJxJwffiq2tLY4eOYKQOTPV1xR7QX5+Pk6fPo3i4mKIxWI0NTXB1dUVUVFRXJxGe8zMzDBhwoSnTuH69eETnLxeiJE2Q7B+9oswMdLfMy/LspwmhK2tLd5///1OI3mA/h4Mw2D//v3YuHFjn0byvVW8G0j2jbpSYL9HW3CeXyTw6g71NoomaodWLk/9P9klv+6h0dmtU+2jXwPCk3R7jOcNlqXf93mQytaGVDEtFevyKlUf1aNS5dy5c6FQKNQezIODg1FbW4uUlBQAVL/D398fV65cwfTp0wHQdN+pU6fi4sWLmD27d/EUWts3IUTrl4+PDxlISBqayXdX88npG4/I/NdfJ6CTyWqvBQsWkD179hB3d3eNn7d/hYeHc3/PmzePiEQiAoB4eXkRuVxOzpw5QxiG6bTfOHuGOFgNIQCIk5MTqa2t7XSu9fX15McffyQHDx4ko0aN6vIcJk2aRJRKJSGEkIyMDHL48GGNr9jYWCKTybS+Vr/99htxcXHp8RoEBQWRr7/+mjuOWCwmM2bM4D4/8s03hCRHE3JoGiG/7CBEper6oI+uEfLvLYRknSE5OTnEzMxM7VgrVqzQeK0GOjY2NuSzzz7rts2+ffsINc/OxMfHE29vbzJkyBAydOhQ4uvrS3755ZdO7QCkkkFs36TqISH/iSIk/RQhLPtsj12eQcjnpoT81YCQz4cQcvvIsz1+fyFvIuTcRkIOBxCSdrz7tvf+Re278OqzObd+QiaTEaFQSA4cOKC2/dixY0QgEBCJREIIIWTbtm3E3t6+0/4uLi4kMjKSe69r++7z0IUQgjKpDCJDAaxMjfDd1QL8nFUG71HWeHfWizA06B+d76KqBnyZkIUmuQofzHXHD3FxOHz4MMaNG4eAgACcPHkSIpEIYWFhYBgGa9asgVgsRkVFRae+MjMzkZCQgJiYGG5bVlYWFxtQVFSEW7duYevWrSCEwMPDA2+88QaUDTX4n/0HkVFOADRybaOjo7F06VKur4KCAmzatIkbOQN05iA4OFhNEdDGxgbr1q2DgYEB18bLq7M+wdPg6+uLtLQ0iMViVFVVwcHBAevWrUNJSQliYmLQ3NyMyZMnc1P37Vm7di1WrlyJmJgYnDz0N6wMzqUjrLI7NKd4ioaI/pJUOv3XMp22L90P9fX1sLS0xLvvvgt/f38sWNAHjfFBSm5uLhYtWoQPP/wQu3fvhkwmw61bt1BdrYc1ZwAsS1Bc0whrUyMYGRpg34UcZJZIEDJpBBb6alGbXV8UptD0KiNzwGuJbmVUmyR05N8xHbU9dl7Ammu02JTDJJor/0fg4ma6DKKU0WwYq9GaVfbSjgHn3msR6fkbsPKyejnhQURubi4UCgU8PNQj9ceOHQuWZXH//n1MmTIF2dnZndq0tmuVcdeHfffJyRNCsCs+E0nppSAECJo4DEnpZZApVMitqIeliRArXtGQ9/kM+DDmFkolTSCE/p3w5xlYv77N2Sxbph6xa2pqisjIyI7dAKDlSJ2cnFBfX89te/SoTeu+trYWfn5t+alHjx7F1Kl0DSg1PadT4NiuXbuwa1fnCnPOzs7w9vaGj48PNm/eDCOjZ6uSZGFhgc2b1YvzjBkzRi2PXBOCyiy8aXoJMQANpGuN9lc00ghZTRRcptHEAPYkN2L/hUsA6LXZsGFDX77GoObOnTswNzfH7t27uW3BwcF6OZZcyWL9kRvILafLRgFudkjOqUCzkkVeRT0cbYZgqms/ZAXIpMB3QTRqmxHQ1M0P7ve9X5alZU/vJ9AI7BUXuheWcZjQd036gcCD80D8qpbAXmv1OhyV9zQ7+Xv/arsPqORA/s+D1sm3xokNHaqup2FlZaX2eU1NTac2re3y8mhckj7su09OvlQiw8X0Uq7EZGLaY654TbOCxYPy+u521wq5ksU/Lj3A/dJa/GmKk9Y1dculMrQuZ7IsgaRB/tSKQ0OHDkVCQgI++fS/cDe3hOuXYQCXdvnNIpEIGzZs4Bw8ABw/fhwRERFwcHDAli1bsH37dly7dk2tf4ZhMG/ePOzcuRPGxv1Y5/ppiVtKg2MAyOol9AYJAdVJHb9c8z6OLwMGRlAolIi4QDd99NFHeOcdHanxDVLGjx8PqVSKt956C8uXL8e0adO00uF/Gn59+AT5FfWcaM+1B5VobrF1lYpFYWVDn528pEGOvUk5qK6XY+0MV4xz0kJ4qKGiTYmNsDR1VBcUXAbyLtJIcLkCSFgPrO/iIfWPgkoJ/HNhm8NuqqbZDAxD09pc52jeb/QsIK+diJCupHYHOfqw7z45eZGhgHN4AFXuanXyABA4tpuCJVqy70IOzt4upjnFxRLYWxprpUAWNHE4LmWWAaCOeFgfC2cEBgZiy/5T+Dw+k9tmLDTA5S2zug38GjlyJE6fPs29P3jwYJ/O47lEVgOzlkmHKwUEI/9uCgMBaEDUoW7qSyvMUVerAtAMc3NzREdHP4uz1SmlkibsTshCvUyJ915zwyTnLrT7dYS7uzvi4+PxxRdfIDg4GEKhEGFhYdizZw9eeEFLkREtMTEy4GrNMQxgLBSgUU4DPZUs4Ova97Sfzd/fwb0SKZQswe+PanAmYnrPFeysRtMMjifZdHQ5/s3u22tL+vftcrqhXr/9jwqr4GbcKARYGg9ICwDXuV3L3PpuoCp5RVcBz8XAqMBncbY6J6NYgn0XcmAsNMDm+Z5wtO6cfdU6YpdKpWrbW0fwrZ9bWVmhsrKy0/41NTVcG33Yd5+cvI25CB/Mc8f+pByIhAYYPtQE9x7T6GuhAYOaBnkPPQDNChX++kM6bhdWw3e0Df4SNh5Cw7Z16KwSKTd6YAmQX9mglZPf8oYXZnnZo0mhQoCbXZ919GVyFb48d6/DMTwHd3EObZkVhWmN72CVtwqFTWb4+V5Vr3Y3MTHBgQMHuvz814dPcOHuY3g5DsWfXnJ6rgoebfr2FgqfNIAQ+vfZyECYm+i3JG1ISAhCQkIglUpx7tw5REREYOPGjV2m5j0tL7lYI3jicJy9XQw7C2POwQO00qSkUdFjH0/qmvHpqTQUVTUg7CUnvPPqGDWbyauo5wYGNL6nqWcnLzCgVc4enAOMzLoeTfaGsrtA+om294wB8Lq47/0OdIQmVPXvZktuuc87wBgN6XMdYRhaI6OHOhmEEPx4uwR3Cqsx09MB0z36PjDUFU1yJT44lopGuQoMA3xwLBWnN03v1M7V1RVCoRDZ2dkIDGx7mMnOzoZAIICbmxsAwMPDQ2OqXHZ2NkJD27QTdG3ffQ68W+Q7EotaAnC+OJuJh+V1UKgIDAQC2Fn0PPV84loBrj6ohFzJ4j/ZFYi78UitGEbIpGHIeiwFIXTqPr+yruvO2sEwDPxe1N3IRq5iwbabpRAwwExP3Rc2AICfM8twOasc3i7WCPVxfP4fJCaFg3F5Fd+8XYUaoSMk7dLsmuUqpD2qhoWJEcZ2kYtua2vLpSB2JKNIgk9O3oFMweJyVjma5CqsCHDRy9d4Gh7XNHGzWYQAVfXNenfyrVhaWuLNN9/ElStXcP36dZ33zzAMNs/3xOb5tMTsSvF1mpJK6M3ZxqznmJHoHzORVSKBigW+v14IHxdrNQ3vGWPtkJj2GASATMHicU0TPIZroVkgNO6bymRHZDUdZFodgRG9EF/RFpYFftsLlNygYi9u+omn0Clzv6LOHaRTHfuaBjnuFFTD2dYUrva9l4COv1WM/z2fzdl39LLJ/RPnoQFJo4LT0iAEKJM2cSmu7RGJRJg5cyZiY2Oxbl2bPsipU6fg5+cHS0v6/xwUFISdO3ciJSUFAQEBAIDU1FTk5eVpFCLTlX3rNDH4/TlueFLXjJyyWgRNGI5X3Ht2stX1cihaRupyJYuqenU1O5/RtjAUCKBQ0TY/3CjGxjn60RvuDgsTIRb4OOLcnRIQAMv9R+klc+DXh0+w40w6ZAoWyTk00j/spV7oNffGlHZRAAAEGElEQVQXlo6ApSOsAFi16ADIlSze+sc1lEtpffIV08ywZmbvashnFkvR8tNDpmBxM6/quXLyQROHIeluGcAAjlZDuOm848ePY/Xq1cjNzYWzszMKCwtx8+ZNAFTZLisrC3FxcTA1NVUz8J9++gkNDQ1IS6NrwXFxVPxoypQpcHZ2hlgsxvXr1zFv3jwMHz4cDx48QGxsLMLDw/X+XXctnoi//HAXVXXNWDtzjFZV86rqm7nfj2HQaXbPb4wtLmaUcXE9R5PztI670SlO0wCHyTRinLDAa1/q5zhXo2l5ZkUjkBNP9eEHwnq1rVunTU/qmrH871ehULFgCcGORRN7PRJPza/mYj6aFVTm+Xlx8vYWxnC1N0d+JV3Cme5hxzn4jva9bds2zJgxAxEREQgNDUViYiISExNx/nybVLqfnx/mzJmD8PBwfPXVV5wYTkBAAJcjrw/71qmTNzMW4qvl3r3aZ6GvExJ/p0FbAgYI7eDQzI0N0X52duiQZzNK0sRH8z2x9GVnGAgYjNCwNqMLMookXBU0mYLF7fzqgeHkNXC/rBblUhk3zfvPG4967eS9XaxgIAAUKromPEMHcR665JPXvRDoYY8GuRKvuNlxD34sy0KlUnFiNpcvX8aqVau4/WJjYxEbGwtnZ2cUFBRw29evX4/CwrZAssWLFwMAjhw5gpUrV2LChAk4e/YsIiMjUV1djWHDhuHtt9/Gjh0dhGD0wAjrITj8toYqiN2wduYYfHoqDQYMA2szI/i7qT/425iLOPs2EAB25v0UeGpgSNO8KrNo2qe5fmoWIP+yeunakhsDw8lrICWnAs1KFeekv79W0GsnH+hhh5ScCsgULIyEgn6r1KYJgYDBgVVTkJxTCZFQgGntZoY72ndAQADi4uKwdetWHDhwAC4uLjhx4oSa2h1AR/ebNm3C6tWr1WRtW9GHfT8XinfSRjnyKxsw2s4MFhqmOv+dUYq9F3JgKjLEjkUT8KJDP+k3PwPuPqrBxuOpkCtYiIQCbAsdh1nj9HTD0TMVUhkW701Gs5KFgAHch1ngyLre39AyiyVIzq6E23BzzBxr//wvXzwnPC+KdxVSGcqkTXAbZgFjYedgtm+u5CLuxiM4WZti15KJsDXvRRGTgUaqGLgQSdX4hCbAmusDNg3vRm4VPvr+DmQKFYQGAoRMGo5PFvRetyMlpwIZRVK8/KKt3gNXBxPa2nevnDzDMJUAdJSvwsPDo2ecCSFaB6bw9s3DM6DQyr575eR5eHh4eHh4Bg79oznLw8PDw8PDo3d4J8/Dw8PDwzNI4Z08Dw8PDw/PIIV38jw8PDw8PIMU3snz8PDw8PAMUngnz8PDw8PDM0jhnTwPDw8PD88ghXfyPDw8PDw8gxTeyfPw8PDw8AxS/h8zJVv1pEV3IAAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Author: Alexandre Gramfort \n",
"# Albert Thomas \n",
"# License: BSD 3 clause\n",
"\n",
"import time\n",
"\n",
"import numpy as np\n",
"import matplotlib\n",
"import matplotlib.pyplot as plt\n",
"\n",
"from sklearn import svm\n",
"from sklearn.datasets import make_moons, make_blobs\n",
"from sklearn.covariance import EllipticEnvelope\n",
"from sklearn.ensemble import IsolationForest\n",
"from sklearn.neighbors import LocalOutlierFactor\n",
"\n",
"print(__doc__)\n",
"\n",
"matplotlib.rcParams['contour.negative_linestyle'] = 'solid'\n",
"\n",
"# Example settings\n",
"n_samples = 300\n",
"outliers_fraction = 0.15\n",
"n_outliers = int(outliers_fraction * n_samples)\n",
"n_inliers = n_samples - n_outliers\n",
"\n",
"# define outlier/anomaly detection methods to be compared\n",
"anomaly_algorithms = [\n",
" (\"Isolation Forest\", IsolationForest(behaviour='new',\n",
" contamination=outliers_fraction,\n",
" random_state=42)),\n",
" (\"Local Outlier Factor\", LocalOutlierFactor(\n",
" n_neighbors=35, contamination=outliers_fraction))]\n",
"\n",
"# Define datasets\n",
"blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)\n",
"datasets = [\n",
" make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5,\n",
" **blobs_params)[0],\n",
" make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5],\n",
" **blobs_params)[0],\n",
" make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, .3],\n",
" **blobs_params)[0],\n",
" 4. * (make_moons(n_samples=n_samples, noise=.05, random_state=0)[0] -\n",
" np.array([0.5, 0.25])),\n",
" 14. * (np.random.RandomState(42).rand(n_samples, 2) - 0.5)]\n",
"\n",
"# Compare given classifiers under given settings\n",
"xx, yy = np.meshgrid(np.linspace(-7, 7, 150),\n",
" np.linspace(-7, 7, 150))\n",
"\n",
"plt.figure(figsize=(len(anomaly_algorithms) * 2 + 3, 12.5))\n",
"plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05,\n",
" hspace=.01)\n",
"\n",
"plot_num = 1\n",
"rng = np.random.RandomState(42)\n",
"\n",
"for i_dataset, X in enumerate(datasets):\n",
" # Add outliers\n",
" X = np.concatenate([X, rng.uniform(low=-6, high=6,\n",
" size=(n_outliers, 2))], axis=0)\n",
"\n",
" for name, algorithm in anomaly_algorithms:\n",
" t0 = time.time()\n",
" algorithm.fit(X)\n",
" t1 = time.time()\n",
" plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)\n",
" if i_dataset == 0:\n",
" plt.title(name, size=18)\n",
"\n",
" # fit the data and tag outliers\n",
" if name == \"Local Outlier Factor\":\n",
" y_pred = algorithm.fit_predict(X)\n",
" else:\n",
" y_pred = algorithm.fit(X).predict(X)\n",
"\n",
" # plot the levels lines and the points\n",
" if name != \"Local Outlier Factor\": # LOF does not implement predict\n",
" Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])\n",
" Z = Z.reshape(xx.shape)\n",
" plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='black')\n",
"\n",
" colors = np.array(['#377eb8', '#ff7f00'])\n",
" plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])\n",
"\n",
" plt.xlim(-7, 7)\n",
" plt.ylim(-7, 7)\n",
" plt.xticks(())\n",
" plt.yticks(())\n",
" plt.text(.99, .01, ('%.2fs' % (t1 - t0)).lstrip('0'),\n",
" transform=plt.gca().transAxes, size=15,\n",
" horizontalalignment='right')\n",
" plot_num += 1\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"np_pred_ys: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]\n"
]
}
],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import warnings\n",
"warnings.filterwarnings(\"ignore\")\n",
"\n",
"import numpy as np\n",
"import xgboost as xgb\n",
"from sklearn import datasets, model_selection, ensemble, metrics\n",
"\n",
"rng = np.random.RandomState(42)\n",
"\n",
"# Generate train data\n",
"X = 0.3 * rng.randn(100, 2)\n",
"np_train_xs = np.r_[X + 2, X - 2]\n",
"\n",
"# Generate some abnormal novel observations\n",
"np_outlier_xs = rng.uniform(low=-4, high=4, size=(20, 2))\n",
"\n",
"# fit the model\n",
"model = ensemble.IsolationForest(behaviour='new', max_samples=100, random_state=rng, contamination='auto')\n",
"model.fit(np_train_xs)\n",
"\n",
"np_pred_ys = model.predict(np_outlier_xs)\n",
"\n",
"# 1: normail, -1: outlier\n",
"print(\"np_pred_ys: {}\".format(np_pred_ys))"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3.8.9 64-bit ('skp-n4e-jupyter-sts')",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.9"
},
"nikola": {
"category": "",
"date": "2019-05-25",
"description": "",
"link": "",
"slug": "ml-anomaly-detection",
"tags": "",
"title": "Machine Learning - Anomaly Detection",
"type": "text"
},
"toc": {
"base_numbering": 1,
"nav_menu": {},
"number_sections": true,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": false,
"toc_position": {},
"toc_section_display": true,
"toc_window_display": false
},
"vscode": {
"interpreter": {
"hash": "074780be484a97690bb59ec71f684629e06fa9a846f324f8f10540b41bb15945"
}
}
},
"nbformat": 4,
"nbformat_minor": 4
}