{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Descriptive Data Analysis\n",
    "\n",
    "기술적 데이터 분석 "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<style>.container { width:100% !important; }</style>"
      ],
      "text/plain": [
       "<IPython.core.display.HTML object>"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "python ver=3.8.9 (default, Jun 12 2021, 23:47:44) \n",
      "[Clang 12.0.5 (clang-1205.0.22.9)]\n",
      "pandas ver=1.2.4\n",
      "numpy ver=1.23.1\n",
      "scipy ver=1.9.0\n"
     ]
    }
   ],
   "source": [
    "# 경고 메시지 출력 끄기\n",
    "import warnings \n",
    "warnings.filterwarnings(action='ignore')\n",
    "\n",
    "# 노트북 셀 표시를 브라우저 전체 폭 사용하기\n",
    "from IPython.core.display import display, HTML\n",
    "display(HTML(\"<style>.container { width:100% !important; }</style>\"))\n",
    "from IPython.display import clear_output\n",
    "\n",
    "%matplotlib inline\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "import os, sys, shutil, functools\n",
    "import collections, pathlib, re, string\n",
    "\n",
    "rseed = 22\n",
    "import random\n",
    "random.seed(rseed)\n",
    "\n",
    "import numpy as np\n",
    "np.random.seed(rseed)\n",
    "np.set_printoptions(precision=5)\n",
    "np.set_printoptions(formatter={'float_kind': \"{:.5f}\".format})\n",
    "\n",
    "import pandas as pd\n",
    "pd.set_option('display.max_rows', None) \n",
    "pd.set_option('display.max_columns', None) \n",
    "pd.set_option('display.max_colwidth', None)\n",
    "pd.options.display.float_format = '{:,.5f}'.format\n",
    "\n",
    "import scipy as sp\n",
    "\n",
    "import seaborn as sns\n",
    "\n",
    "from pydataset import data\n",
    "\n",
    "print(f\"python ver={sys.version}\")\n",
    "print(f\"pandas ver={pd.__version__}\")\n",
    "print(f\"numpy ver={np.__version__}\")\n",
    "print(f\"scipy ver={sp.__version__}\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "<class 'pandas.core.frame.DataFrame'>\n",
      "Int64Index: 150 entries, 1 to 150\n",
      "Data columns (total 5 columns):\n",
      " #   Column        Non-Null Count  Dtype  \n",
      "---  ------        --------------  -----  \n",
      " 0   Sepal.Length  150 non-null    float64\n",
      " 1   Sepal.Width   150 non-null    float64\n",
      " 2   Petal.Length  150 non-null    float64\n",
      " 3   Petal.Width   150 non-null    float64\n",
      " 4   Species       150 non-null    object \n",
      "dtypes: float64(4), object(1)\n",
      "memory usage: 7.0+ KB\n"
     ]
    }
   ],
   "source": [
    "# Iris 데이터 셋의 컬럼 정보 살피기\n",
    "df_iris = data('iris')\n",
    "df_iris.info()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>Sepal.Length</th>\n",
       "      <th>Sepal.Width</th>\n",
       "      <th>Petal.Length</th>\n",
       "      <th>Petal.Width</th>\n",
       "      <th>Species</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>5.10000</td>\n",
       "      <td>3.50000</td>\n",
       "      <td>1.40000</td>\n",
       "      <td>0.20000</td>\n",
       "      <td>setosa</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>4.90000</td>\n",
       "      <td>3.00000</td>\n",
       "      <td>1.40000</td>\n",
       "      <td>0.20000</td>\n",
       "      <td>setosa</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>4.70000</td>\n",
       "      <td>3.20000</td>\n",
       "      <td>1.30000</td>\n",
       "      <td>0.20000</td>\n",
       "      <td>setosa</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>4.60000</td>\n",
       "      <td>3.10000</td>\n",
       "      <td>1.50000</td>\n",
       "      <td>0.20000</td>\n",
       "      <td>setosa</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>5</th>\n",
       "      <td>5.00000</td>\n",
       "      <td>3.60000</td>\n",
       "      <td>1.40000</td>\n",
       "      <td>0.20000</td>\n",
       "      <td>setosa</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   Sepal.Length  Sepal.Width  Petal.Length  Petal.Width Species\n",
       "1       5.10000      3.50000       1.40000      0.20000  setosa\n",
       "2       4.90000      3.00000       1.40000      0.20000  setosa\n",
       "3       4.70000      3.20000       1.30000      0.20000  setosa\n",
       "4       4.60000      3.10000       1.50000      0.20000  setosa\n",
       "5       5.00000      3.60000       1.40000      0.20000  setosa"
      ]
     },
     "execution_count": 3,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df_iris.head()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>Sepal.Length</th>\n",
       "      <th>Sepal.Width</th>\n",
       "      <th>Petal.Length</th>\n",
       "      <th>Petal.Width</th>\n",
       "      <th>Species</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>count</th>\n",
       "      <td>150.00000</td>\n",
       "      <td>150.00000</td>\n",
       "      <td>150.00000</td>\n",
       "      <td>150.00000</td>\n",
       "      <td>150</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>unique</th>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>3</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>top</th>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>versicolor</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>freq</th>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>50</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>mean</th>\n",
       "      <td>5.84333</td>\n",
       "      <td>3.05733</td>\n",
       "      <td>3.75800</td>\n",
       "      <td>1.19933</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>std</th>\n",
       "      <td>0.82807</td>\n",
       "      <td>0.43587</td>\n",
       "      <td>1.76530</td>\n",
       "      <td>0.76224</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>min</th>\n",
       "      <td>4.30000</td>\n",
       "      <td>2.00000</td>\n",
       "      <td>1.00000</td>\n",
       "      <td>0.10000</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>25%</th>\n",
       "      <td>5.10000</td>\n",
       "      <td>2.80000</td>\n",
       "      <td>1.60000</td>\n",
       "      <td>0.30000</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>50%</th>\n",
       "      <td>5.80000</td>\n",
       "      <td>3.00000</td>\n",
       "      <td>4.35000</td>\n",
       "      <td>1.30000</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>75%</th>\n",
       "      <td>6.40000</td>\n",
       "      <td>3.30000</td>\n",
       "      <td>5.10000</td>\n",
       "      <td>1.80000</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>max</th>\n",
       "      <td>7.90000</td>\n",
       "      <td>4.40000</td>\n",
       "      <td>6.90000</td>\n",
       "      <td>2.50000</td>\n",
       "      <td>NaN</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "        Sepal.Length  Sepal.Width  Petal.Length  Petal.Width     Species\n",
       "count      150.00000    150.00000     150.00000    150.00000         150\n",
       "unique           NaN          NaN           NaN          NaN           3\n",
       "top              NaN          NaN           NaN          NaN  versicolor\n",
       "freq             NaN          NaN           NaN          NaN          50\n",
       "mean         5.84333      3.05733       3.75800      1.19933         NaN\n",
       "std          0.82807      0.43587       1.76530      0.76224         NaN\n",
       "min          4.30000      2.00000       1.00000      0.10000         NaN\n",
       "25%          5.10000      2.80000       1.60000      0.30000         NaN\n",
       "50%          5.80000      3.00000       4.35000      1.30000         NaN\n",
       "75%          6.40000      3.30000       5.10000      1.80000         NaN\n",
       "max          7.90000      4.40000       6.90000      2.50000         NaN"
      ]
     },
     "execution_count": 4,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# describe()을 통한 대략적인 데이터의 통계량 알아보기\n",
    "df_iris.describe(include='all')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 대표값\n",
    "\n",
    "데이터 분석을 위해서 데이터 특성을 이해하기 위해서는 데이터의 특성을 나타내는 몇몇 통계량을 구해봄으로써 데이터를 전체적으로 빠르게 파악해 볼수 있습니다.\n",
    "\n",
    "일반적으로 많이 쓰이는 대표값은 평균값(Average), 중앙값(Median), 최빈값(Mode) 입니다.\n",
    "\n",
    "* 평균값: 평균의 데이터의 중심을 나타내는 대표값으로 사용됩니다. 평균의 종류에는 산술평균, 가중평균, 조화평균, 기하평균 등 많은 평균의 종류가 있지만 간단하게 산술평균을 많이 사용합니다.\n",
    "* 중앙값: 중앙값은 데이터를 작은 순서로 나열했을때 중앙에 위치하는 값입니다. 데이터에 이상치(큰 값)가 포함되어 있더라도 강건(Robust, 값이 크게 흔들리지 않음)합니다. 데이터의 갯수가 짝수일 경우 중앙 값은 중앙 두 데이터의 평균을 사용합니다.  \n",
    "* 최빈값: 데이터를 계층으로 나누어 빈도수를 측정하였을때 그 빈도수가 가장 많은 값입니다. \n",
    "\n",
    "만약, 데이터에 이상치가 포함되어 있지 않고, 데이터의 분포가 치우치지 않았다면, 평균값, 중앙값, 최빈값 모두는 비슷한 위치에 존재하게 됩니다. 이때는 통계적으로 다루기 쉬운 평균값을 대표값으로 사용하는 것이 일반 적입니다.\n",
    "\n",
    "데이터가 이상치를 포함하고 있다면 평균값은 이상치에 민감하기 때문에 3가지 대표값이 서로 다룬 위치에 존재하게 됩니다. 이 경우 데이터의 도메인 특성에 따라 이상치를 제거하는 등의 방법을 통해 평균을 대표값으로 사용할 수 있습니다.\n",
    "\n",
    "![](https://i0.wp.com/upload.wikimedia.org/wikipedia/commons/c/cc/Relationship_between_mean_and_median_under_different_skewness.png?w=578&ssl=1)\n",
    "\n",
    "https://www.r-bloggers.com/2020/11/skewness-and-kurtosis-in-statistics/\n",
    "\n",
    "@최빈값의 활용: 과거 대칭방식의 암호해독시에 문서상에서 나타나는 알파벳의 최빈값과 암호화된 알파멧의 최빈값을 비교하여 해독의 기준점으로 많이 사용하였다고 합니다.  "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Sepal.Length   5.84333\n",
       "Sepal.Width    3.05733\n",
       "Petal.Length   3.75800\n",
       "Petal.Width    1.19933\n",
       "dtype: float64"
      ]
     },
     "execution_count": 5,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# 평균값\n",
    "df_iris.mean()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Sepal.Length   5.80000\n",
       "Sepal.Width    3.00000\n",
       "Petal.Length   4.35000\n",
       "Petal.Width    1.30000\n",
       "dtype: float64"
      ]
     },
     "execution_count": 6,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# 중앙값\n",
    "df_iris.median()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>Sepal.Length</th>\n",
       "      <th>Sepal.Width</th>\n",
       "      <th>Petal.Length</th>\n",
       "      <th>Petal.Width</th>\n",
       "      <th>Species</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>5.00000</td>\n",
       "      <td>3.00000</td>\n",
       "      <td>1.40000</td>\n",
       "      <td>0.20000</td>\n",
       "      <td>setosa</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>1.50000</td>\n",
       "      <td>NaN</td>\n",
       "      <td>versicolor</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>NaN</td>\n",
       "      <td>virginica</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "   Sepal.Length  Sepal.Width  Petal.Length  Petal.Width     Species\n",
       "0       5.00000      3.00000       1.40000      0.20000      setosa\n",
       "1           NaN          NaN       1.50000          NaN  versicolor\n",
       "2           NaN          NaN           NaN          NaN   virginica"
      ]
     },
     "execution_count": 7,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# 최빈값\n",
    "df_iris.mode()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "그외 알아보면 평균들: 산술평균, 기하평균, 조화평균, 등등"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 데이터의 분산\n",
    "\n",
    "**산포도(Dispersion)**\n",
    "\n",
    "산포도는 데이터의 흩어짐 정도를 나타냅니다. 같은 데이터의 대표값을 가지더라도 데이터의 산포도는 다를 수 있기 때문에 대표값과 더불어 데이터의 특성을 파악하는데 중요하게 사용됩니다. \n",
    "\n",
    "### 히스토그램(Histogram)\n",
    "\n",
    "데이터의 분포를 히스토그램을 통해 시각적으로 확인해 볼 수 있습니다."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "array([[<AxesSubplot:title={'center':'Sepal.Length'}>,\n",
       "        <AxesSubplot:title={'center':'Sepal.Width'}>],\n",
       "       [<AxesSubplot:title={'center':'Petal.Length'}>,\n",
       "        <AxesSubplot:title={'center':'Petal.Width'}>]], dtype=object)"
      ]
     },
     "execution_count": 9,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEICAYAAABGaK+TAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAdxElEQVR4nO3df7QcZZ3n8feHBCUkYNBkMzEBLg4MyJoRNPJjQCYLxAEBYecoRxY5ZAcmM2dhhDXrEN3dUc+OTphBRx0ZPQhKHBgYFmFhwRllIZcfiiABBEJAEIMEA4gQIIg/At/9o56GTqf73rp9u2/V0/fzOqdPuqq6ur7dt+qbp5+nnudRRGBmZvnZpuoAzMysO07gZmaZcgI3M8uUE7iZWaacwM3MMuUEbmaWKSfwCSRpnaTDq45jJJJC0u5Vx2GDqVfXgKRdJG2SNKXD9k9KumiE/ZdIumW8cVRt0iZwSQdL+p6k5yQ9I+m7kt5VYTzDkk4d9GNafdTpGpB0gqS1Leuu67BueUT8NCJmRMTLJd57KBVMpvY67qpNygQuaUfgGuAfgDcC84BPAb+uMi6ziVLDa+AmYC9Js1N8U4G3A9Na1h2YXmtM0gQO/B5ARFwSES9HxEsR8Z2IuAdA0p9IWivpWUnflrRrY8f0P/mHJT0i6WlJfydpm7TtdyXdIOkXadvFkmaON9gS8fy5pIckbZR0riSlbVMkfTbF8hNJpzdKIpI+Dbwb+FL6KfqlpkMe3u79bKDU6hqIiMeBR4BD0qp3AGuAG1vWbQP8oLVULWk3STdKekHSdcCsprdvJPyN6Vw/sOmznJM+408kHTnG77BykzWB/wh4WdJKSUdK2qmxQdKxwMeBPwZmAzcDl7Ts/x+BhRQn1LHAnzR2B/4GeDPwVmBn4JPjCbRkPEcD7wJ+Hzge+KO0/k+BI4F9UqzHNXaIiP+e3uv09FP09BLvZ4OjjtfATbyWrA9Jx72lZd33I+K3bfb9Z2A1ReL+X8DJTdsa+89M5/qtaXl/4MG0z98CF2RXWImISfmgOLkuBNYDm4GrgTnAvwKnNL1uG+CXwK5pOYAjmrb/F+D6Dsc4DriraXkdcHiH1w4Dp7ZZXyaeg5u2XwYsT89vAP6sadvh6fVTOx1zpPfzY7AeNbwGljReC1wFLAb2aln3ifR8qHEuA7uk+Kc3vdc/Axe1vrblWA83LW+fXvM7Vf9dxvKYrCVwImJtRCyJiPnA2yhKDJ8HdgW+kKoPNgLPUJQq5jXt/ljT80fTvkiaI+lSSY9Leh64iC1/ynWjTDxPND3/JTAjPX9zS6zNz0fS6f1sgNTwGrgJ+P30a+AA4NaIeACYm9YdTPv67zcDz0bEiy0xjebV8zwifpmeZnWuT9oE3iydJBdSnMSPUZRaZzY9pkXE95p22bnp+S7Az9Lzz1D8L74gInYEPkRx4o9HmXg62QDM7xA3KVazWlwDEfFIep+lwE8jYlPadGtaNwP4fptdNwA7SZreEtOrb13m+DmalAlc0l6Slkman5Z3Bk6gODm+AnxM0r9P294g6QMtb/FRSTul/c4A/iWt3wHYBDwnaR7w0TGGNlXSdk2PbUvG08llwBmS5qWGpLNatj8JvGWMMdoAqPE1cDPwkfRvwy1p3R0R8VLrDhHxKHAH8ClJr5N0MHBM00t+DrzCAJ7rkzKBAy9QNGDcJulFipP2PmBZRFwJnA1cmn4C3kfRENjsKooGk7uBa4EL0vpPUTTqPJfWX9EpAEknSlrTsvrLwEtNj6+XjKeTrwLfAe4B7gK+RVFX2Lh39gvA+1Mr/BdLvqcNhrpeAzcC/44iaTfcnNaNdPvgf0qf5xngE8A3GhtS9cinge+maqEDRnifrChV4FtJkgLYIyIerjqWsUq3SX0lInYd9cVmHeR8DQyayVoCnxQkTZP0XhX3fc+jKJlcWXVcZtYbTuCDTRQ/aZ+lqEJZC/xVpRGZWc+4CsXMLFMugZuZZWpCR+eaNWtWDA0NTeQht/Diiy8yffr00V84gRzT6JrjWb169dMRMbvikEob6Zyv2/fcS/5svdXxvJ/Ibp/vfOc7o0qrVq2q9PjtOKbRNcdDcS9w5V2Yyz5GOufr9j33kj9bb3U6712FYmaWKSdwM7NMOYGbmWVq4KYY6oeh5deOeZ91K47qQyRm9da4VpYt2MySkteNr5XuuQRuZpYpJ3Azs0y5CqVmXF1jZmW5BG5mlikncDOzTDmBm5llygnczCxTTuBmZplyAjczy5QTuJlZppzAzcwy5QRuZpaprHtijrXX4rIFm1nUn1DMzCZc1gncrB8kbQfcBLye4hq5PCI+IWk34FLgTcBq4KSI+E11kQ4GDx/RPVehmG3t18ChEfF2YB/gCEkHAGcDfx8RuwPPAqdUF6KZE7jZVtI0hJvS4rbpEcChwOVp/UrguImPzuw1rkIxa0PSFIpqkt2Bc4EfAxsjYnN6yXpgXod9lwJLAebMmcPw8HDbY2zatKnjtlwtW1B8PXOmvfa8H6r83ur0d3MCN2sjIl4G9pE0E7gS2GsM+54HnAewcOHCWLRoUdvXDQ8P02lbrpY0zcjz2Xv7l17Wnbiob+89mjr93VyFYjaCiNgIrAIOBGZKamSl+cDjVcVlBiUSuKSdJa2SdL+kNZLOSOvfKOk6SQ+lf3fqf7hm/Sdpdip5I2kasBhYS5HI359edjJwVSUBmiVlSuCbgWURsTdwAHCapL2B5cD1EbEHcH1aNhsEc4FVku4BfgBcFxHXAGcBH5H0MMWthBdUGKPZ6HXgEbEB2JCevyBpLUXjzbHwar+YlcAwxQlulrWIuAfYt836R4D9Jj4is/bG1MogaYjixL4NmJOSO8ATwJwO+5Rqke/GWFu550zrrvW6m9b0ssdpbdHu57HKqlMrO9QvHrO6KJ3AJc0AvgmcGRHPS3p1W0SEpGi3X9kW+W4s6aIr/fFdHH+sx4HyreStLdr9PFZZdWplh/rFY1YXpe5CkbQtRfK+OCKuSKuflDQ3bZ8LPNWfEM3MrJ0yd6GIorFmbUR8rmnT1RQt8eAWeTOzCVemCuUg4CTgXkl3p3UfB1YAl0k6BXgUOL4vEZqZWVtl7kK5BVCHzYf1NhwzMyvLPTHNzDLlsVAGgMdTNpucnMDNbCvdFAps4rkKxcwsU07gZmaZcgI3M8uUE7iZWabciGk24NwgObicwPuk7EWzbMHmrgawMjNzFYpZC89CZblwAjfbmmehsiw4gZu1iIgNEXFnev4CxXyYjVmoVqaXrQSOqyRAs8R14GYj6OcsVBM101A3szyN15xp/T1ulTM01WmGKCdwsw76PQvVRM00VEUj+bIFm/nsvf1LL72ehWos6jRD1KRL4L6lysoYaRaqiNjgWaisDlwHbtbCs1BZLiZdCdysBM9CZVlwAjdr4VmoLBeuQjEzy5QTuJlZppzAzcwy5QRuZpYpJ3Azs0w5gZuZZWrUBC7pa5KeknRf0zoPq2lmVrEyJfALgSNa1nlYTTOzio2awCPiJuCZltUeVtPMrGLd1oGXGlbTzMz6Z9xd6UcaVhPKj43cjbGON9zvMYq7UVVMI/0d6jTeMdQvHrO66DaBlx5Ws+zYyN0Y6zjH/R6juBtVxTTSeMp1Gu8Y6hePWV10W4XiYTXNzCo2atFP0iXAImCWpPXAJ+jxsJqeZMHMbOxGTeARcUKHTR5W08ysQu6JadaGO7BZDurVomdWHxcCXwK+0bSu0YFthaTlafmsCmKzLnRbVbtuxVE9jqR3XAI3a8Md2CwHTuBm5bkDm9WKq1DMujBSB7ayndcmqoNSFR3F+t1B7R8uHvudy8sWdHes1r9RnTqWOYGblVeqA1vZzmsT1UFprB3eeqGOnea61drprU4dy1yFYlaeO7BZrTiBm7WROrDdCuwpaX3qtLYCWCzpIeDwtGxWmcH4jWNjNtItVcsWbG77s7vb26m6uX2r6lu33IHNcuASuJlZppzAzcwy5SoUK82DjlXPfwNr5hK4mVmmnMDNzDLlBG5mlikncDOzTDmBm5llygnczCxTvo3QrCL3Pv5cJQNN2eBwCdzMLFNO4GZmmXICNzPLlBO4mVmm3IhpZjaC1vFnOg23PF7dDKHsEriZWabGlcAlHSHpQUkPS1req6DM6srnvNVJ1wlc0hTgXOBIYG/gBEl79yows7rxOW91M54S+H7AwxHxSET8BrgUOLY3YZnVks95q5XxNGLOAx5rWl4P7N/6IklLgaVpcZOkB8dxzHH5MMwCnq7q+O04pvZ09haLzfHsOuHBvKbX53zl33O/1OEc6pd+fbaWc75V2/O+73ehRMR5wHn9Pk4Zku6IiIVVx9HMMY2ubvGMpuw5n9vnGgt/tokxniqUx4Gdm5bnp3Vmg8rnvNXKeBL4D4A9JO0m6XXAB4GrexOWWS35nLda6boKJSI2Szod+DYwBfhaRKzpWWT9UYuqnBaOaXS1iKcP53wtPlef+LNNAEVE1TGYmVkX3BPTzCxTTuBmZpmaNAlc0jpJ90q6W9IdNYhnpqTLJT0gaa2kAyuOZ8/03TQez0s6s8qYUlz/VdIaSfdJukTSdlXHNB6Sdpa0StL96XOdUXVMvSJpO0m3S/ph+myfqjqmXpM0RdJdkq6pOhaYRHXgktYBCyOiFp0LJK0Ebo6I89MdDdtHxMaKwwJe7TL+OLB/RDxaYRzzgFuAvSPiJUmXAd+KiAurimm8JM0F5kbEnZJ2AFYDx0XE/RWHNm6SBEyPiE2StqX4250REd+vOLSekfQRYCGwY0QcXXU8k6YEXieS3gAcAlwAEBG/qUvyTg4Dflxl8m4yFZgmaSqwPfCziuMZl4jYEBF3pucvAGspenhmLwqb0uK26TEwJURJ84GjgPOrjqVhMiXwAL4jaXXq6lyl3YCfA19PP8fOlzS94piafRC4pOogIuJx4Bzgp8AG4LmI+E61UfWOpCFgX+C2ikPpmVTFcDfwFHBdRAzMZwM+D/wl8ErFcbxqMiXwgyPiHRQjyZ0m6ZAKY5kKvAP4ckTsC7wI1GJo0lSd8z7gf9cglp0oBovaDXgzMF3Sh6qNqjckzQC+CZwZEc9XHU+vRMTLEbEPRS/V/SS9reKQekLS0cBTEbG66liaTZoEnkpzRMRTwJUUI8v1naRPSrqoZfV6YH1T6eRyioReCUkXSvrrtHgkcGdEPFlVPE0OB34SET+PiN8CVwB/UHFM45bqh78JXBwRV1QdTz+kKsFVwBEdroGuSPpXSSd32DYkKVJ1W6f9Q9LuXRz6IOB9qS3tUuDQXn2m8ZgUCVzS9NRgRKqqeA9wX7oz5SVJmyQ9mRLZjFHea1jSqeOJJyKeAB6TtFzSLRR1zhPSiCVpSTpmJydQg+qT5KfAAZK2Tw1kh1HUGWcrfY4LgLUR8bkaxNOza0DSbEkz0/NpwGLggRHeZ2o67v5N605MSbZ13QMAEXFkRKws+dnGfa02RMTHImJ+RAxRVDHeEBGV/xqcFAkcmAPcIumHwO3AtRHxb2nbMRExg6IEvBD4HxMU018Af0ZRB7oP8JkJOm5H6T+3xRQl3cqlXyiXA3cC91Kcr7Xpxtylg4CTKEpwjVs231txTL26BuYCqyTdQzFuzHUR0fF2u4jYDNxK0aDfcAhF0m9dd1OXMQ22iJi0D2AdcHjT8t8B1wAHAN8DNgI/BBal7Z8GXgZ+BWwCvpTWf4FinOjnKW4Le3fTe34SuKjD8ZcAt3TYthdwHfAM8CBwfNO2CylmhrkWeIGiEex3m7a/J+3zHPCPwI3AqcBbU+wvp/g3lnk/Pwb3UYNr4H8C/7dp+f50XbSu+1B6Pgycmp5PoWjkfhp4BDiN4maFqSPEGcCfAw+lz3Yu6XbqHB+VB1CXk5dimNA1wFeBXwDvpSjxLU7Ls1tPoKb3+RDwpnTiLAOeALYrcfIuoU0CB6ani+E/p/fcN52ke6ftF6aY9kvbLwYuTdtmpYvoj9O2M4DfNp30Wx1zpPfzY7AfNbgG/pCikLJNOncfpbhd9MmmdQHs0nrslIgfSHG/kaLOPYCpI8QZFP9BzQR2obgb7Iiq/w7dPiZLFcpI/o+kjRSdDm6kaGD8VkR8KyJeiYjrgDsoTua2IuKiiPhFRGyOiM8Crwf2HEdMRwPrIuLr6T3vomj0+kDTa66MiNuj+Bl6MUU1DCnONRFxRdr2RYqLaTSd3s8GX5XXwG0UCXsB8G6KwsUvgZ80rVsXET9ts+/xwOcj4rGIeAb4m5Kfd0VEbEzvuYqMz/W+z8iTgeMi4v81FiT9I/ABScc0vWZbij90W5L+G3AKxa1uAexIUXLo1q7A/umiapgK/FPTcnNS/iXQaHh6M03TfkVESFpf4pid3s8GX2XXQET8StLtFPXcbwFuTptuaVrXqf57i3OdovRexsCc607gW3sM+KeI+NMO27foWSbp3RQ39x9GUfJ9RdKzgMYZw40RsbiLfTdQ3IPbiE/NywxQzzjrm4m+Bm6iSNa78Vovx5spqmV2A77cYb8NbDlD0i4jxTmIXIWytYuAYyT9UepVtp2kRakbLRR1c29pev0OwGaKurSpkv6KovRRltIxXn1Q1NH9nqSTJG2bHu+S9NYS73ctsEDScel+2NOA32na/iQwP3XYMWtnoq+Bm4D/QJGMG7fTfhdYRFG90akEfhnwYUnzU6ev1s5wrXEOHCfwFhHxGEXvv49TnJCPAR/lte/qC8D7JT0r6YsUs7P8G/Ajip9wv2LLn3VbSPe9vrtp1R8AL7V5vIfiftOfUfzkO5uiXnG0+J+mqCv/W4qGp70p6i9/nV5yA0VD1ROSajGwl9VLBdfA94A3ALdFo6WxOI9/TtH78aEOb/XVdOwfUtxq2nr7a2ucA2fSjEY4WUnahqJR6sSI6FiHaWb5cQl8AKWfvjMlvZ6iFCVgYIb0NLOCE/hgOhD4McW948dQ3GXwUrUhmVmvuQrFzCxTLoGbmWVqQu8DnzVrVgwNDU3kIXnxxReZPr1OcyWMzjF3tnr16qcjYnbfD9Qjs2bNitmzZ2f39ywrx3O1rDp9tk7n/YQm8KGhIe64Y2LnEx4eHmbRokUTeszxcsydSarDNG+lDQ0Ncc4552T39ywrx3O1rDp9tk7nvatQzMwy5QRuZpYpJ3CzDlI38rskXZOWd5N0m6SHJf2LhyOwqtViMKuh5dd2td+6FUf1OBKzLZxBMYVbY1yPs4G/j4hLJX2FYvS9TgMtjaqb897nvDVzCdysjTRw01Gk0fHSqI6HUkzxBrASOK6S4MySWpTAzWro8xRDpO6Qlt9EMQXd5rS8HpjXbkdJS4GlAHPmzGHTpk0MDw9v9bplCzZvtW407d6nSp0+2yDI4bM5gZu1kHQ0xSh4qyUtGuv+EXEeafLlhQsXxowZM9rejrakmyqUE8ccTl/V6Va7XsvhszmBm23tIOB9abb47SjqwL8AzJQ0NZXC5wOPVxijmevAzVpFxMciYn5EDFGMyX5DRJxIMaXY+9PLTgauqihEM8AJ3GwszgI+IulhijrxCyqOxyY5V6GYjSAihoHh9PwRYL8q4zFr5hK4mVmmnMDNzDLlBG5mlikncDOzTDmBm5llygnczCxToyZwSdtJul3SDyWtkfSptN5Da5qZVahMCfzXwKER8XZgH+AISQfw2tCauwPPUgytaWZmE2TUBB6FTWlx2/QIPLSmmVmlSvXElDQFWA3sDpwL/Jguh9bs1bCaUG5ozRyGhGzlmG0y8cQW3SuVwCPiZWAfSTOBK4G9yh6gdWjNXg2rCeWG1sxhSMhWjtnMyhjTWCgRsVHSKuBAPLRmbbgEYzY5lbkLZXYqeSNpGrCYYp5AD61pZlahMiXwucDKVA++DXBZRFwj6X7gUkl/DdyFh9Y0M5tQoybwiLgH2LfNeg+taWZWIffENDPLlBO4mVmmnMDNzDLlBG5mlinPiVkzQ8uvZdmCzV13bjKzycMlcDOzTDmBm5llygnczCxTTuBmZplyAjczy5QTuJlZppzAzcwy5QRuZpYpJ3Azs0w5gZuZZarMjDw7S1ol6X5JaySdkda/UdJ1kh5K/+7U/3DNzKyhzFgom4FlEXGnpB2A1ZKuA5YA10fECknLgeXAWf0L1cyse2OdO7YxJlGd548dtQQeERsi4s70/AWK+TDnAccCK9PLVgLH9SlGMzNrY0yjEUoaophe7TZgTkRsSJueAOZ02GcpsBRgzpw5DA8Pb/WaZQs2jyWMV7V7r1abNm0q9bq6WLZgM3Omdf+dlNXr7yS379lsEJRO4JJmAN8EzoyI5yW9ui0iQlK02y8izgPOA1i4cGEsWrRoq9d0O3TquhO3fq9Ww8PDtDtmXS1Jw8l+9t7+jvRb5rsbi9y+Z7NBUOouFEnbUiTviyPiirT6SUlz0/a5wFP9CdFsYrnh3nJR5i4UARcAayPic02brgZOTs9PBq7qfXhmlWg03O8NHACcJmlviob66yNiD+D6tGxWmTIl8IOAk4BDJd2dHu8FVgCLJT0EHJ6WzbLnhnvLxagVrRFxC6AOmw/rbTg2UcZ6SxVQ69up+qUXDfedGni7aaiuW0NxLxqvJ+p7GOtxGjcT1O07b+Y5Mc066FXD/YwZM9o28HbTeN/rxufx6kXj9UR9D2M9TuNmgrp9583cld6sDTfcWw6cwM1auOHecuEqFLOtNRru75V0d1r3cYqG+ssknQI8ChxfTXhmBSdwsxZuuLdcuArFzCxTTuBmZplyAjczy5QTuJlZppzAzcwy5QRuZpaprG8jLDOeR2NapIbJOJ6HmQ2mrBO4mVkdTdRgca5CMTPLlBO4mVmmyszI8zVJT0m6r2mdp5YyM6tYmTrwC4EvAd9oWteYWmqFpOVp+azeh2d1MlK9XmtjcTM3HJv1x6gl8Ii4CXimZbWnljIzq1i3d6GUmloKtp5eqldTS5XVmBapoc7TI0ERa2vMORgp5rp/52a5GvdthCNNLZW2bzG9VK+mliqrMS1SQ52nR4Liu2iNOQcjxVz379wsV93eheKppczMKtZtAvfUUmZmFStzG+ElwK3AnpLWp+mkVgCLJT0EHJ6WzcxsAo1a0RoRJ3TY5KmlRtBNV1ozq586X8vuiWlmlqm8bnUwm+QmapCkbtW5tDqIXAI3M8uUS+BmtpWyJemRhlCw/nMJ3MwsU07gZmaZchWKmWXHjaUFJ3Dru7rfOWGWK1ehmJllygnczCxTTuBmZplyHXgJbjAxszpyCdzMLFNO4GZmmXICNzPLlBO4mVmmxpXAJR0h6UFJD0ta3qugzOrK57zVSdd3oUiaApwLLAbWAz+QdHVE3N+r4MzqJNdz3ndRDa7xlMD3Ax6OiEci4jfApcCxvQnLrJZ8zlutKCK621F6P3BERJyalk8C9o+I01tetxRYmhb3BB7sPtyuzAKenuBjjpdj7mzXiJg9AcfZyjjO+V+Q39+zrBzP1bLq9Nnanvd978gTEecB5/X7OJ1IuiMiFlZ1/G445ry1nvOD/N34s1VrPFUojwM7Ny3PT+vMBpXPeauV8STwHwB7SNpN0uuADwJX9yYss1ryOW+10nUVSkRslnQ68G1gCvC1iFjTs8h6p7Lqm3FwzDU0jnN+kL8bf7YKdd2IaWZm1XJPTDOzTDmBm5llaiATuKSdJa2SdL+kNZLOqDqmsiRNkXSXpGuqjqUMSTMlXS7pAUlrJR1YdUx1Mqhd7yV9TdJTku6rOpZeyyl/DGQduKS5wNyIuFPSDsBq4Li6d3kGkPQRYCGwY0QcXXU8o5G0Erg5Is5Pd2ZsHxEbKw6rFlLX+x/R1PUeOCGH83A0kg4BNgHfiIi3VR1PL+WUPwayBB4RGyLizvT8BWAtMK/aqEYnaT5wFHB+1bGUIekNwCHABQAR8Rsn7y0MbNf7iLgJeKbqOPohp/wxkAm8maQhYF/gtopDKePzwF8Cr1QcR1m7AT8Hvp6qfc6XNL3qoGpkHvBY0/J6apoIrL2654+BTuCSZgDfBM6MiOerjmckko4GnoqI1VXHMgZTgXcAX46IfYEXgYGp57XJLYf8MbAJXNK2FF/+xRFxRdXxlHAQ8D5J6yh+ah8q6aJqQxrVemB9RDRKJ5dTJHQruOt9pnLJHwOZwCWJol52bUR8rup4yoiIj0XE/IgYouiifUNEfKjisEYUEU8Aj0naM606DKhdQ0+F3PU+Qznlj4FM4BSl2ZMoSrF3p8d7qw5qQP0FcLGke4B9gM9UG059RMRmoNH1fi1wWU2HmxgzSZcAtwJ7Slov6ZSqY+qhbPLHQN5GaGY2GQxqCdzMbOA5gZuZZcoJ3MwsU07gZmaZcgI3M8uUE7iZWaacwM3MMvX/ASEfuGSxDMcQAAAAAElFTkSuQmCC",
      "text/plain": [
       "<Figure size 432x288 with 4 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "df_iris.hist(bins=10, grid=True)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 18,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAbYAAAGpCAYAAADhiRM+AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAABgbElEQVR4nO3dd3gc1dX48e/Zoi5ZlizbsmVZ7sZV2LIDxhRjQyCQAIFAgNBCSQLkDSGNVEIqyZv6y5uQmE4glNB7MzamGtw7tnGvcpdk9d3z+2PGIIxkq+zubDmf59lHu7O7M0cr3T1z79wiqooxxhiTLHxeB2CMMcZEkiU2Y4wxScUSmzHGmKRiic0YY0xSscRmjDEmqQS8DqA9evTooWVlZV6HYUynzZs3b5eqFnkdx0FWpkwyaKtcJURiKysrY+7cuV6HYUynicgGr2NoycqUSQZtlStrijTGGJNULLEZY4xJKpbYjDHGJBVLbMYYY5KKJTZjjDFJxRKbMcaYpGKJzRhjTFKxxBbHSvuXISJdvqWlp0dkP6X9y7z+SIyJqtLSko6Xi9ISr8M2h0iIAdqpatPGDczeWtPl/ZzQJydi+zEmmW3atIWZM2/u0HumTLklStGYzrIamzHGmKRiic0YY0xSscRmjDEmqVhiMyZBiEiGiLwnIotEZJmI3OJuv0dE1onIQvdW7nGoxnjKOo8YkzgagJNVtUZEgsCbIvKC+9z3VPVRD2MzJm5YYjMmQaiqAge7twbdm3oXkTHxyZoijUkgIuIXkYVAJfCKqs5xn/q1iCwWkT+LSHob771GROaKyNydO3fGKmRjYs4SmzEJRFVDqloOlAATRWQU8ENgODABKAB+0MZ7p6tqhapWFBXFzWLexkScJTZjEpCq7gNmAqep6jZ1NAB3AxM9Dc4Yj1liMyZBiEiRiOS79zOBU4CVIlLsbhPgbGCpVzEaEw+s84gxiaMYuFdE/DgnpY+o6rMi8pqIFAECLAS+7mGMxnjOEpsxCUJVFwNHt7L9ZA/CMSZuRa0pUkT6ichMEVnuDib9lrv95yKypcVg0s9FKwZjjDGpJ5o1tmbgO6o6X0RygXki8or73J9V9Q9RPLYxxpgUFbXEpqrbgG3u/WoRWQH0jdbxjDHGGIhRr0gRKcO5NnBwMOn17mDSu0SkexvvscGkxhhjOizqiU1EcoDHgBtUtQq4DRgElOPU6P7Y2vtsMKkxxpjOiGpicydqfQx4QFUfB1DVHe7sCWHgdmwwqTHGmAiKZq9IAe4EVqjqn1psL27xsnOwwaTGGGMiKJq9Io8DLgGWuJO2AvwIuNBdL0qB9cDXohiDMcaYFBPNXpFv4syEcKjno3VMY4wxxuaKNMYYk1RsSq0E0xxWapvD1IeUhpDSHIaQOmtN+gT8IgR9QppfSPcJGYHWKs3GGJO8LLHFufrmMFVNYaobnZ+1zZ9cMNlJZs79sDq3Q5dU/vGry1myu4HMgJAZELICPrIDPtL8lvSMMcnHElscaQ4rO+qa2XqgmS0HmrjphUXM29UAOMkrN+ijR46fnKCPDL+Q7hd88snkpKo0KzSElMaQUhcK88jjL9DngsvZ0xCiqe7j1wZ9kBP0kRPw0S3NR26a71P7M8aYRGOJLUbCqlS7Na+aprBzv+ng/RA1TWGqGsOE3OpWXtDH+gXvcs6XLiAvzUdWQJB2JB0RISgQ9AkEAfw88avv8O1rnc6nTW5T5oEmpaYpzIHmMHsbmtl0wLng2j3dR1FmgO7pluSMMYnJEluU1DeHWVPVyNqqJirrmtnbEPooaR3kF6fGlBv00TszwLBufoqzA/TJCpCb5ue60V/j2ssvjmhcQZ/QLc1Pt7SPtzWHlarGMPsaQ+yqD7G7oZGgD/pkBSjOCuD3WYKLByKSAcwG0nHK7qOqerOIDAAeAgqBecAlqtroXaTGeMsSWwul/cvYtHFDl/aRkZPHWTf+nIlfvJTGsJIdEIqzggzKS6N7up/coM9JZmk+Mv3tq4VFW8AnFGT4KcjwMyBX2dsYZtuBZjbUNLOtNsTAvCCFGX6vwzTQAJysqjXurD5visgLwI04K2Y8JCL/BK7EmbrOmJRkia2FTRs3MHtrTaffv7chxJr9jdQ1NjO4WxrjizLokxWIi+TVXiJCQbqfgnQ/VY0hPqxqYuW+Rnpm+glmZHodXkpTVQUO/oMG3ZsCJwMXudvvBX6OJTaTwmwcW4TsqG1m+d5G/D7htstO4wtlufTNDiZUUjtUXpqf8sJ0SrIDVNaF+Nqdz3KgKex1WClNRPzuTD6VwCvAh8A+VW12X7KZNpaHshUzTKqwxBYB22ubWVPVRH6aj7EF6WxZscjrkCJGROifG+So/DSKygZx/+p97G8MeR1WynInEC8HSnAmEB/egffaihkmJVhi66L9DSHWukntqO5pSdvRoiDDz53fOI/aZuXhNVXUNlvNzUuqug+YCRwL5IvIwcsKJcAWr+IyJh5YYuuCxpCycl8jGX5hWH5a0neP37h4LucNzKOqMcR/P6yiKXzoUHATTSJSJCL57v1M4BRgBU6CO8992WXAU54EaEycsMTWSarKh1WNhBWGd08jkKQ1tUP1ywnyhbJcttU288qmzne0MZ1SDMwUkcXA+8Arqvos8APgRhFZg9Pl/04PYzTGc9YrspN214fY0xCmf26ArEBqnR8MzU9nUq9m3t5RR9+cIGMLM7wOKSWo6mLg6Fa2r8UW7DXmI6n1jRwhIVXWVTeRHRD6ZqXmucHk4iz65wR5dXMN+xqsM4kxJn5YYuuEbQeaaQzDgLzE7s7fFT4Rzuifgw/h2Q3VqNr1NmNMfLDE1kFNYWXzgWa6p/volpbas3HkpfmZWpLN5gPNLNhV73U4xhgDWGLrsG21zYQU+ucEvQ4lLowuSKc0J8jsbbXU2uBtY0wcsMTWASFVtrm1teygfXTgDOA+tSSbxpAya9sBr8MxxhjrFdkRlXUhmhVKsu1ja6lHZoDxRRm8v7OeCUWZFGXa52MSX1XVZnbvXkU43EReXj969BiOiJ3QJgL7BmonVWXrgWZyg0Ku1dY+ZVLvLBbvbmD2tlrOHZjndTjGdFoo1MiqVc9SWbkEEHw+P5s3v0tWVhEjRnyJ7GybjizeRe0bWkT6ichMEVkuIstE5Fvu9gIReUVEVrs/u0crhkja1ximPqQUJ9hs/bGSGfAxsVcmq/c3svVAk9fhGNMpwSAsXvwAlZVL6d//RI477gdMnvxDRow4n6amWhYuvJuamh1eh2mOIJpVj2bgO6o6AjgGuE5ERgA3ATNUdQgww30c97bXNhP0YeuSHUZFUQZZAeH1rbVeh2JMp5xxBlRVbeSoo86lrOwkAoF0RHwUFR3F0Udfic8XYOnS/9DUZP/j8SxqiU1Vt6nqfPd+Nc6cdn2Bs3DWjML9eXa0YoiUhpCypyFMz8xA0s8H2RXpfh/H9spiQ00T66ttAWeTWJYufZjycigtPZ6ePUd+6vnMzO6MGnUhjY01rF79fOwDNO0Wk4tFIlKGMxXQHKCXqm5zn9oO9GrjPXGzdlRlnbPUVa/M9tXWxO9HRLp8S0RH98ggOyC8u6PO61CMabfa2l0899zX2bwZ+vc/sc3X5eYW07//iezcuYydO5fHMELTEVHvPCIiOcBjwA2qWtXyC1tVVURanbJCVacD0wEqKio8m9ZCVamsC5EX9JHZzjkhNRTq0krcB53QJ6fL+4i1gE+Y0DOTWVtr2V7bTO8UnXLMJJbXX/8FDQ3VPPUUXHzx4U9g+/U7jl27VrJmzQsUFAyJUYSmI6JaYxORIE5Se0BVH3c37xCRYvf5YpyVgONWTbNSH1J6trO2ZqC8RwbpPmHODrsOYeLf7t2rmTv3NsaNu4r2NA75fH4GDz6NxsYatmyZE/0ATYdFs1ek4CyfsUJV/9Tiqadx1oyCBFg7amddM4J1GumIDL+P8h4ZrNzXyF6bIDliDtPT+OciskVEFrq3z3kdayKZNetn+P3pnHTSz9v9nm7dSikoGMrGjW+SmRm92EznRLPGdhxwCXDyIQXuVuAUEVkNTHMfx6WwKrvqQxRk+FNmvbVIqeiZgU/gvUq71hZBbfU0Bvizqpa7N+vZ0E579nzIsmWPMGHCdeTk9O7QewcOnEoo1MCxx0YpONNpUbsAoqpvAm1lg6nROm4k7W8M0xSGIqutdVhu0M/I7uks3VPPicVZZKTYmnXR4Ha62uberxaRgz2NTSe9884f8fkCHHPMDR1+b3Z2T3r0OIoJE1bQ0FBNenpu5AM0nWLfNoexuz6ET6B7un1MnTGuKJOmMCze0+B1KEnnkJ7GANeLyGIRuautSQ/iqadxPDhwoJKFC+9mzJhLyc0t7tQ++vU7jsxMmDdveoSjM11h39htUFX2NIQoSPfb2LVO6p0VoG92gPk762y9tgg6tKcxcBswCCjHqdH9sbX3qep0Va1Q1YqiIpsWav78O2lurmfSpO90eh95eX1Ztw7effdPhEI2djNeWGJrQ5XbDGmdRrpmfI9M9jWGWVdt02xFQms9jVV1h6qGVDUM3A5M9DLGRKAaZv782ykrm0KPHsO7tK+334bq6q0sX/5YhKIzXWWJrQ27G0L4gO5p9hF1xbD8NLIDwryd1omkq9rqaXxw+IzrHGBprGNLNB9++Ar79q1j/PivdXlfa9ZA9+6DeP/9v0cgMhMJ9q3dClVld32I/HQffusN2SV+n1DeI4MPq5rYZ13/u6qtnsa/F5ElIrIYmAJ829Mo40hpaUmrs/r85CenceAAlJd/ucuz/ajChAnXsWnTW2zbtiDCv4HpDJsWohU1TUqjNUNGzNjCDN7eXsfi3fWc0Cfb63AS1mF6Glv3/jZs2rSFmTNv/sS2hoZq3n33z/TrdyyvvnrKJ56bMuWWTh2nvPxyZs78Ce+//3e+8IU7Oh2viQyrsbVid0MIAQrSLbFFQl6an4F5QRbvaSBsnUiMx7Zvnw8oxcXjI7bPzMzujB79FZYs+Q91dXsitl/TOZbYWrGnPkS3NJ8Nyo6gMYUZ1DSFWVtlnUiMd1SV7dsXkZ8/gMzMgojue+LE62hurmPBgrsjul/TcZbYDlEfClMXUvKtthZRg7ulkRUQFu2u9zoUk8KqqjZTX7+XXr3GRHzfvXqNobR0MvPm/ROng6rxiiW2Q+xrcP4hbVB2ZPlFGF2QwYf7G6lpskJvvFFZuRifL0CPHkdFZf8VFd9gz541rFv3WlT2b9rHvr0PsbchRLpPyPRbM2SkjSlMJwws3WO1NhN74XCIysplFBYOJxBIj8oxjjrqXLKyejB37m1R2b9pH0tsLfgDQfY1hslP9yXsQp/xrDAjQEl2gCfeXxGRhVhL+5d5/SuZBLJnzxqam+vo1Wt01I4RCKRTXv5VVq58iqqqLVE7jjm8dnX3F5HjVPWtI21LdKVjJxBW6G7X16JmbGEGm/v255n1++mW1rXPOREXYj0oVcpUPKmsXEIwmEX37oOiepzx46/h7bd/z4IFd3LiiT+L6rFM69pbY/tbO7cltGHHTUWAbjbbSNQMy0+nvqaayrqUH6ydEmUqXjQ317N79wcUFY3E54vuiWtBwSAGDfos8+ZNJxxujuqxTOsOW2MTkWOBSUCRiNzY4qk8IOmqNUMnnUyedfOPqjS/sHTGM2SffRED8xR/ijX5plqZihe7dq0gHG6OSm/I1lRUfIOHHz6bVaueY/jws2JyTPOxI1VN0oAcnASY2+JWBZwX3dBiq7oxRPHQUeRbbS3qFjz3CCF1xgumoJQpU/Fkx44lZGR0Jzc3NsvXDR16Bnl5JdaJxCOHrbGp6uvA6yJyj6puiFFMnljrzj5v19eib928t0nzCTvrQhRlptasbqlUpuJFQ0MV+/ato3//E2PWKcznCzBu3NXMmnUze/eupXv3gTE5rnG0t3qSLiLTReRlEXnt4C2qkcXY2qpG9u/YSlYgtZrGvKCq9Mz0s7cxTGMoZafYSvoyFS8qK5cA0LNn9HpDtuboo69ExM/cuf+K6XFN+ydB/i/wT+AOIOnaj8KqrK9uYtXbr/G5sdHtMWUcRZl+Nh9oZmd9M32zg16H44WkLlPxZMeOJeTm9iUrqzCmx83L68vw4WexcOFdTJnyi6iNnTOf1t4aW7Oq3qaq76nqvIO3qEYWQ1sONNMQUla9bSfMsZIV8JETdJojU1SHy5SI9BORmSKyXESWici33O0FIvKKiKx2f3aPza8Q/3r2hAMHdsSs08ihxo//OrW1u1ixwhYhjaX2JrZnRORaESl2C1GBiBx2BlERuUtEKkVkaYttPxeRLYesJeW5dVWNCLBmzuteh5JSemYEONCsHEjNKbY6XKaAZuA7qjoCOAa4TkRGADcBM1R1CDDDfWyAMWMAhKKikZ4cf+DAqRQUDLZOJDHW3sR2GfA94G1gnnube4T33AOc1sr2P6tquXuLi3WkPqxqpG92gPqaKq9DSSk9Mv0IpOqYtg6XKVXdpqrz3fvVwAqgL3AWcK/7snuBs6MTcmJRDTN6NBQUDCYtzZt1AEV8jB//dTZufJPKSlvYPFbaldhUdUArt8N281HV2UDcL0x0oCnMjroQA/PSvA4l5QR9Qvd0Hzvrm9EUW6etM2WqJREpA44G5gC9VHWb+9R2oFcb77lGROaKyNydO3d29VeIexs2zKZbN6I6hVZ7lJdfjt+fzty5//Q0jlTS3im1Lm1tu6re14ljXu/uby5Os8reNo55DXANQGlpaScO0z5rqxoBLLF5pCgzwJ6GRvY1hlNqqEVXypSI5ACPATeoalXLLuyqqiLS6lmCqk4HpgNUVFQk/ZnE4sUP0NgIhYXDPI0jK6uQkSPPZ9Gi+5g69Tekp+d5Gk8qaG9T5IQWt+OBnwNf6MTxbgMGAeXANuCPbb1QVaeraoWqVhQVFXXiUO2zrrqJrIDQKzN1vlTjSUG6D7+kZHNkp8qUiARxktoDqvq4u3mHiBS7zxcDldEIOJE0N9ezfPl/WbEC/H7vT1o/85n/obGxmvnz7/Q6lJTQrhqbqn6z5WMRyQce6ujBVHVHi33cDjzb0X1EUliVdVWNDOqWZrP5e8QnQlGGn8q6EM1hTZnpzDpTpsT5J70TWKGqf2rx1NM41+xudX8+FdFgE9Dq1c/T0LCfxYu9jsTRp08F/fufwJw5f+Uzn/kmPl9qTUwQa52dP+oAMKCjbzp4Vuk6B/D0aur22mbqQsrAXO/P6FJZUaafMLA7NafYOqg9Zeo44BLg5EN6Ft8KnCIiq4Fp7uOUtmTJA2Rn92LdOq8j+dixx36H/fs3sHy5df2PtvZeY3sGONgm7weOAh45wnseBE4CeojIZuBm4CQRKXf3tR74WmeCjpS1Vc40WgPyUnKAcNzIDfrI8AuV9SF6ZaXGmWxnypSqvgm0VaWdGrnoEltd3V5WrXqWiopvEA7/1etwPjJ06JkUFg7lnXf+yMiR51srURS191vkDy3uNwMbVHXz4d6gqhe2sjmuGpjXVjXSJytAZsAmPvaSiNAz08/Gmmbqm8NkpMbfo8NlyrTPihWPEQo1MmbMV4D4SWwiPo455kaee87p/t+///Feh5S02tvd/3VgJc4s5N2BxmgGFQt1zWG21jZbb8gOEL8/Iitft6Yow+m8szNFmiOTsUzFi8WL76ewcCjFxeO9DuVTxo69lKysHrzzTpv95kwEtLcp8nzgf4FZOE0hfxOR76nqo1GMLarWuc2QA60Zst00FGL21pou76e1la8zAj7ygj4q60KUZAeSvpkmGctUPNi/fyMbNrzOSSf9Ii7/h4LBTCoqrmX27F+ya9cH9Ojh7VCEZNXeNp8fAxNU9TJVvRSYCPw0emFF39rqRjL9Qu8UuaaTCHpm+qkPKdWpMcVW0pWpeLBkyYMAjB59kceRtO1rX5tOU5Ny9dXD29XCUVpa4nXICae93+o+VW05NmY3ne9R6TlVZW1VIwPy0vDF4VldqirM8LO2qonKuhB5aUk/rjCpylQ8UFUWLbqHfv0mUVAQv6t0rF69nbKyYwgG53DNNd8kM/Pwc1ZPmXJLjCJLHu0tSC+KyEsicrmIXA48B8TFPI+dsaMuRG2zMiDXmiHjScAnFGb42VUfIpz8U2wlVZmKB5s3v8uuXSspL/+q16EcUb9+kxDxsWnTm16HkpQOW2MTkcE489B9T0S+CEx2n3oHeCDawUWLTaMVv3pm+tlZH2JPQ5geGclXa0vWMhUPFiy4i2Awm5Ejz/c6lCNKT8+luPhotm2bT2npCWRkdPM6pKRypBrbX4AqAFV9XFVvVNUbgSfc5xLS2qpGemX6yQ5ay0+86ZbmI80HlXXNXocSLX8hCcuU1xoba1i27CFGjjyf9PRcr8Npl379jgNg06a3PI4k+Rzpm72Xqi45dKO7rSwqEUVZfXOYLQeaGWS1tbgkIhRlBtjbEKYxlJTNkUlXpuLB8uWP0thYw9FHx38z5EEZGfn06jWWbdvm09BQ7XU4SeVIiS3/MM9lRjCOmFlf3YQCAyyxxa2e7oTUu5JzTFv+YZ5LyDIVDxYsuJPCwqEf1YISRWnpZFTDVmuLsCMltrkicvWhG0XkKpyFERPO2qpG0v1C32zr5h+vsgI+cgKSrM2RSVemvLZ79yo2bnyT8vKvxuXYtcPJzCygd++xbN06l4YGW+g4Uo707X4D8ISIXMzHha4CSMOZxDihqCprq5soyw1aN/841zMzwNrqJg40hZPtWugNJFGZigcLFtyFiJ+xY1td4i7u9e9/Ijt2LGbDhtkMHXqm1+EkhcMmNneZmUkiMgUY5W5+TlVfi3pkUbCzPkRNU9h6QyaAHpl+1lU7Y9oGJFFiS7Yy5bVQqJFFi+5lyJDTyc0tPvIb4lBGRj7FxePYtm0+/fodd8RxbebI2jtX5ExV/Zt7S9gC+FE3fxu/FveCPqF7uo+d9c1oEo5p60yZEpG7RKRSRJa22PZzEdlyyDI2KWPFiieoqdlORcU3vA6lS0pLjweEDRtmex1KUkieU+F2+LCqkZ6ZfnKTf1aLpNAzM0BTGPY0pMQUW+1xD3BaK9v/rKrl7i2lBnm///7/0b37QAYPbu1jSRzp6Xn06TOBHTsWUVu7y+twEl7KJLb6UJjNNdbNP5EUpDtj2nbUJmUnkg5T1dnAHq/jiBc7dixm48Y3qaj4BiKJ/1VWWjoZny/A+vWvex1Kwkv8/4Z2Wl/ldPO362uJQ0TolRlgb2OY+pDV2g7jehFZ7DZVtnmBRkSuEZG5IjJ3586dsYwvKt577+8EAhkJNXbtcNLSsikp+Qw7dy6lpmaH1+EktJRJbB9aN/+E1CvLaTbeUZuUY9oi4TZgEFAObAPaXOhLVaeraoWqVhQVFcUovOior9/HkiX3M2rURWRmFngdTsSUlEzC709n/fpZXoeS0FIisR2czX+gdfNPOOl+H93TfVTWJWcnkq5S1R2qGlLVMHA7zvI3SW/+/Dtoaqpl4sTrvA4looLBTPr1O5bdu1dSXb3V63ASVkokth11IQ40qzVDJqhemQEarRNJq0SkZR/3c4Clbb02WYRCjbz77l8oK5tCcfE4r8OJuL59jyEQyGTdupleh5KwUqJd7kObzT+hfdSJpK6ZwiSc8b+9RORB4CSgh4hsBm4GThKRckCB9cDXvIovVpYufYjq6i18/vO3ex1KVAQC6ZSWTmbt2lfYt2+D1+EkpKglNhG5CzgTqFTVUe62AuBhnMle1wPnq+reaMVw0NqqRoqzAsk2g0XKEBF6ZgbYfKCZ+lCYDH9q/h1V9cJWNt8Z80A8UlpawqZNW/iGO2Rt6NDkHbLXp88ENm9+l3XrXvU6lIQUzRrbPcD/Afe12HYTMENVbxWRm9zHP4hiDNQ1h9l6oJlJvW1+2UTWO8vP5gPNbK8NUZabmokt1W3atIXHHruYJUseYNiwszj//PIjvidRV5/2+4OUlZ3EqlXPMHy419Eknqh9Q7Qx5uYs4F73/r3A2dE6/kHr3G7+Nn4tsaX7fRRm+Nle20wobJ1IUtXGjW+RlpZLz56jvQ4l6nr3LicrqwdTp0I4bGM5OyLWp769VHWbe3870KutF0ZqzM2aqkYyA0JxVkpcTkxqfbL8hBQqk3M5G3ME/fvD/v3r6ddvEj5f8l9rFfFRVnYyRUWwaNF9R36D+YhnbTrq9N1u89Q7EmNuQqp8WNXI4Ly0hFvOwnxabtBHTlDYdsC6/qeik06CtLQciovHex3KJ4g414Hbe+uIHj2Gs3kzzJp1M01NdVH6DZJPrKsxO0SkWFW3ud2UK6N5sE01TTSElCHdrBkyGYgIfbICrNrfxL5G6/qfSjZsmM2AAdCv33H4/fE1ibkqzJx5c7tf35HrfiLCq69CSclm3n//70ya9N3OhJhyYl1jexq4zL1/GfBUNA+2al8jAbHVspNJYYafNB9sOWDXHFLJ66/fQnU1cVdbi4X162Hw4NN4443fUF+/z+twEkLUEps75uYdYJiIbBaRK4FbgVNEZDUwzX0cFarKmv2NDMhLI+izZshk4ROhT3aA/Y1hSsdUeB2OiYF162aybt1rvPUWcVdbi5WpU39Lff1e3nrr916HkhCi1hTZxpgbgKnROmZLO+pCVDWFmWzNkEmnd2aAzTXNTLny216HYqJMVXn11e+Tl9ePuXM3eR2OZ3r3Lmf06It4992/UFHxDbp16+d1SHEtKQYElfYv+9QF2ku+82PCoRCTBpdE5aKu8Y7f59Tahh9/KtttSZuktnz5f9m6dS5TpvyC5hT/U5988q8BZcaMm7wOJe4lRR/4TRs3MHtrzSe2LdxVj1+EF5a3f0qaE/rkRDo0EyXFWQFWbdvDOzvSOGdAntfhmCgIhRqZMeNH9Ow5mjFjLgGu8DokT+Xnl3Hssd/ljTd+xYQJ19Gv3ySvQ4pbSVFjO1R9c5gDzUpBRlL+egYI+IR3HrmTD/Y1UlmX4qfySWrevOns3fsh06bdmhLj1tpj8uSbyM3ty4svfgtnQQfTmqT85j84C3xBuhWGZPbGv/9Bul+YtfWA16GYCKut3cXMmT9jwICTGTz4dK/DiRtpadlMm/Y7tm6da4O2DyMpE9vuhhBZASEzkJS/nnHVVe1jUq9M1lY1saG60etwTAeVlrZ9/fuCC4qord3Ld7/7Gj6fz66BtzB69EWUlBzDjBk/pKGh2utw4lJSXGNrqTGkVDWGKbGVslPC+KJM5u2sZ+bWWi4bGrQvwASyadOWVgc2V1dvZf782+nb9zM88shpH21P1AmNI01EOO20v3LHHcfw2ms/4fTT/+p1SHEn6ao0uxuceQR7pPC6Xakk4BOOL85ie20zK/Ymf61NRO4SkUoRWdpiW4GIvCIiq92f3b2MsStUlTVrXiAYzKas7CSvw4lbfftOZMKEa3nvvb+xefMcr8OJO0mX2HbVhcj0C1kBO3NPFSML0umV6ee1LQeoDyX9BfV7gNMO2XZwOaghwAz3cULasWMxVVWbGThwKoFAhtfhxLWpU39Dbm4fnnnmakKhJq/DiStJldgaQ0pVU5geGX5rkkohPhFOK83hQHOY2VtrvQ4nquJlOahoaGqqY+3aV8jN7UuvXuVehxP30tPzOOOMf1BZuYS33vqd1+HElaRKbLvc5Ux6ZFozZKopzgoyriiD+bvq2XIg5c5e27UcVKSWgoqWDz98iebmOoYOPdNOTFs43OoBw4efxZIl8OqrP6Vv34+3l5aWeB22p5Kqh8Xueqc3ZJb1hkxJJxRnsWpfIy9urOGyYfkEUnCOUFVVEWl1TR9VnQ5MB6ioqIirdX/27PmQHTsWUVo6mZyc3l6HE1eOtHpAU1Md8+b9k299K8D48V/D709L+Y42SZMBGlo0Q5rUlO73cVq/HHbWh5iZWmPbdrjLQBGL5aAiLRRqZPXqZ8nMLKR//xO9DifhBIOZDB9+DnV1e1iz5kWvw4kLSZPYdtU7s09YYkttg7qlUVGUwbyd9aza1+B1OLES0+WgIm3duteor9/H0KGfx+dLqkakmMnPL6Nfv8ls376A7dsXeh2O55ImsVXWhcgN2qBsAyf1yaZ3ZoDnN9awvzHkdTgR5fVyUJFWVbWZLVvm0KdPBfn5/b0OJ6GVlZ1Efn4Zq1Y9S9++HVvVO9muySXF6VHxsNHUNisD81JzrSbzSQGfcNaAXO5ZuY9HP6zi4qHdyPAnxwmP18tBRVIgAB988DTp6XkMGDDN63ASns/nZ8SILzF//u1ccME+PvvZ75CW1r6J3ZPtmlxSlPZxZ56PYM2Q5mPd0/2cMyCX3fUhnlhbTSgcV30lDDBlCtTW7mTIkDMJBNK9DicpBINZjBx5ARkZsHTpgzQ3p0xz/CckfGILqVJ++rkUpPtspWzzCWV5aZxemsOGmiae31hDWC25xYv1619n0iQoLh5PYeEQr8NJKjk5vXn0Uaiu3sby5Y8QDidXc3x7JHxiW1fVRE5BET0zk6JV1UTY6MIMTijOYtneBp7dUEPIkpvnGhqqePLJy9i7FwYNOtXrcJLSqlUwbNgX2Lt3LStXPplyS9wkfGJbsqeemr27yE9P+F/FRMmk3lmcWJzF8r0NPLWumuYWzZKtrb7emVtp/zLvfsEE8+KLN1BVtYnHHwe/P83rcJJW797lDBgwjZ07l/LBB0+nVHJL+GrOgNw0/nDHn/nsH//kdSgmjh3bO4ugT3h1ywEeXLOfcwbkkRP0tbr6emfY6uvts3LlUyxceDeTJ/+Im2/+jdfhJL3S0uNQbWb9+lmAMGzYF1JiVpeEr+aU98jg7Qenex2GSQAVPTM5uyyXyrpm7v1gH9tSb+otTx04UMkzz1xN795Hc9JJbc+kYSKrf/8T6d//RHbsWMiqVU+jKdAc70mNTUTWA9VACGhW1Qov4jCpZ3j3dLqn+3lsXRX/XrWfEy77JqqaEmexXlJVnn76KhoaqjjnnH9bE2SMOUsAKRs2zAaEoUM/n9T/817W2KaoarklNRNrvbICXDEsn6H5aZz+rZ+xdG8jDcm/3E1UHW41bBHhmGN8rFr1DM8+20CvXqOS+ks1XvXvfxKlpcezffsCVq9+Nqlrbgl/jc2YzsgM+DirLJdfnnURF/zibyzY1cDAvCBFtuRRp7S1GjZATc125s+/g+7dB/Hb3375o8832QYFxzsRoaxsCqrKpk1vIuJj8ODPJeX/u1c1NgVeFpF5InJNay+I9yU2jPfE7+9ST0afz8f8Zx6ivDCdrICP1fubWLmvkcZQ8p7Jxloo1Mjy5Y8SDGYxfPhZSfklmkhEhAEDTqakZBJbt87lww9fTMqam1c1tsmqukVEegKviMhKdwHFj8TzEhsmPmgo1OUejSf0ySEz4GN0QRpba5vZUN3Mgl31DO6WRqHNZNNlq1e/QF3dbsaMuZRgMMvrcAxOchs4cBoQZvPmd4HkO9nwJLGp6hb3Z6WIPAFMBGYf/l3GRI+I0Dc7SPc0P6v2N7JyXyNFGX4G5gVTcl23SNixYzE7diyktPQEuncf4HU4pgUnuZ2KqrJlyxxOPZWk6kQV86ZIEckWkdyD94FTgaWxjsOY1mQFfYwpTKdfToBd9SEW7Kpnb0PqTUnUVXV1e1i9+jny8kopK7M11uKRiDBo0Gfp02cCkybBjBk/SppmSS9qbL2AJ9wzgwDwH1W11fFM3PCJUJoTpCDdz+r9jSzf20ifrABluYG4PaONpyE04XAzy5f/FxEfRx31RUQSfrhs0hIRBg8+naeeeh+4lWAwixNP/KnXYXVZzBObqq4Fxsb6uMZ0VE7Qx9jCdNZVN7G1tpmapjDD8tNI88dncsMZQrPL6yBWr36emprtjBp1IRkZ3bwOxxyBiPD883D11Zcza9bPCAYzmTTpu16H1SXW3d+Yw/CJMCgvjdxgMx/ub2Lh7nqG56eRl2YdS1qzbdt8tm9fQGnp8RQWDvU6HNNOqvD5z99BU1Mdr7zyPYLBLCZMuNbrsDrN2giMaYeemQHGFKbjF2HpnkZ21cfddTfPh9BUV29j9ernyc8f4M50YRKJz+fnnHP+zbBhX+D5569j4cJ7vA6p0yyxGdNO2W7Hkpygjw/2NbL5QFM8XWyfrKrjgNOB60TkhENfoKrTVbVCVSuKiooievCMDFi+/BHS0rI56qhz7bpagvL7g5x33sMMHHgKTz99JUuXPux1SJ1i/33GdEDQJ4wqSKNHhp8N1c2srYqP5NZyCA1wcAhNTITDIc4911lnbcSIL5GWlh2rQ5soCAQy+PKXn6S0dDJPPPEVVq58yuuQOswSmzEd5BNhaLcgfbMDbK8L8cH+JvxB7yb19XoIzcsvf5chQ2Dw4NPJyyuJ1WFNFAWDWVx44bMUF4/j0UfPZ82al7wOqUMssRnTCSJCWW6QstwAu+tDXPaX+72ciqsX8KaILALeA56L1RCaefOmM2fOX3j3XejTx+YzTybp6blcfPGLFBWN4OGHz2b9+te9DqndLLEZ0wV9s4MMzgtSMmocezwayK2qa1V1rHsbqaq/jsVx162byfPPX8fgwafx8suxOKKJtczM7nzlKy+Tnz+ABx88k02b3vE6pHaxxGZMF/XKCvC/n6+gd1bqjJ6prFzGI4+cS2HhUM499yHCtupP0srOLuLSS18lJ6c3//73NFavfsHrkI7IEpsxEVBXtc/rEGJm374N3H//qQQCGVx44bM2CDsF5Ob24Yor3qCwcCgPPfQFFi26z+uQDssSmzGm3Q4cqOT++0+lqamWSy552SY3TiE5Ob25/PLX6d//BJ588jJeeeUHhMPNXofVqtRpOzHGdElNzXbuu28q+/dv4pJLXqFnz1Feh2QiRIR2z4Pq98NppwH8nu3b5/PFL/6H7OzIjovsKktsxpgjqq7eyr33nkxV1WYuvvh5SkuP8zokE0GqtLkCeltuvPEWvvjFN7jttlGceea/GD787OgE1wnWFGmMOaxduz7g7ruPp7p6Cxdf/IJNl2UAWLAArr76fXJz+/Lww+fw2GMXUlW12euwAEtsxpjDWL/+de6881gaGqq55JJX6d//eK9DMnGkV6/RXHXVHE466RZWrHiCv/1tKDNn3kxDQ5WncVlTpDHmU1SV9977P15++TsUFAzioouet44i5hMOvS6Xnw/TpkFz8y94+eVfMHcuzJkD1dXO8/369WXjxtjU6CyxGWM+oa5uD0899VU++OAphgw5g3PO+TeZmd29DsvEmbauy1VXb2XTprfJyFjO5MlQUDCY3r3HctFFj8YsNktsxphP+O9/z2fDhtmceuqfOOaYG+J21XATn3Jz+zBixHnU1e1h27YF7NixiOXLV/Pd78Kjj36ZoUPPZPDg08nKKoxaDJbYjDGfcOqpfyAcbra5H02XZGYWMHDgVAYMmMLeveu47777KSycxbJlDwNC797llJYeT//+J9C///FkZ/eM2LEtsRljPqF373KvQzBJRMRHQcEgnnoKnnhiK1u3zmP16ufZuHE28+ffznvv/T8ACguHUVJyDH37TqRv34n06jUGv79zq2ZYYjPGfEppaQmbNm3xOgyTREScVbpb8vuhuBj694fS0g/o2/cDcnLuBSAUgiuvdGY66ShPEpuInAb8FfADd6jqrV7EYUyyiHSZ2rRpS4cG7E6ZcktXDmdSQHsGgasqDQ1VVFdv4fbb/8sPfjC8U8eK+Tg2EfEDf8dZwn4EcKGIjIh1HMYkCytTJlmICBkZ3SgqGsErr9Dp625eDNCeCKxx15BqBB4CzvIgDmOShZUpY1oQ1diu+isi5wGnqepV7uNLgM+o6vWHvO4a4Br34TDgg5gG2n49gF1eB9FBFnNstIy5v6pGZabYKJWpRPy8o8U+i0+Kp8+j1XIVt51HVHU6MN3rOI5EROaqakL1i7aYYyPeYu5ImYq32L1kn8UnJcLn4UVT5BagX4vHJe42Y0znWJkypgUvEtv7wBARGSAiacCXgac9iMOYZGFlypgWYt4UqarNInI98BJO1+S7VHVZrOOIoLhvLm2FxRwbMYk5SmUqET/vaLHP4pPi/vOIeecRY4wxJppsPTZjjDFJxRKbMcaYpGKJrQtEZL2ILBGRhSIy1+t42kNE8kXkURFZKSIrRORYr2M6HBEZ5n6+B29VInKD13Edjoh8W0SWichSEXlQRDK8jqm9RKSfiMwUkeXu7/Atr2PyiohkiMh7IrLI/SxSft4wEfGLyAIRedbrWA7HrrF1gYisBypUNV4GKx6RiNwLvKGqd7g96LJUdZ/HYbWLO3XUFpzBxxu8jqc1ItIXeBMYoap1IvII8Lyq3uNtZO0jIsVAsarOF5FcYB5wtqou9zi0mBNnIbpsVa0RkSDO3/Vbqvqux6F5RkRuBCqAPFU90+t42mI1thQiIt2AE4A7AVS1MVGSmmsq8GG8JrUWAkCmiASALGCrx/G0m6puU9X57v1qYAXQ19uovKGOGvdh0L2lbE1AREqAM4A7vI7lSCyxdY0CL4vIPHe6ong3ANgJ3O02J9whItleB9UBXwYe9DqIw1HVLcAfgI3ANmC/qr7sbVSdIyJlwNHAHI9D8Yzb9LYQqAReUdWU/SyAvwDfB8Iex3FElti6ZrKqjsOZVf06Een4wkGxFQDGAbep6tHAAeAmb0NqH7fZ9AvAf72O5XBEpDvOBMQDgD5Atoh8xduoOk5EcoDHgBtUtcrreLyiqiFVLceZzWWiiIzyOCRPiMiZQKWqzvM6lvawxNYF7tk5qloJPIEzy3o82wxsbnHW+ShOoksEpwPzVXWH14EcwTRgnaruVNUm4HFgkscxdYh7Pekx4AFVfdzreOKB22Q/EzjN41C8chzwBbdfwUPAySJyv7chtc0SWyeJSLZ7cR23Oe9UYKm3UR2eqm4HNonIMHfTVCBROgVcSJw3Q7o2AseISJbb+WAqznWqhODGfCewQlX/5HU8XhKRIhHJd+9nAqcAKz0NyiOq+kNVLVHVMpxLAq+paty2RMTt7P4JoBfwhPM9QAD4j6q+6G1I7fJN4AG3aW8tcIXH8RyRe+JwCvA1r2M5ElWdIyKPAvOBZmABCTAFUQvHAZcAS9xrSwA/UtXnvQvJM8XAvW5vXB/wiKrGdTd347Du/sYYY5KKNUUaY4xJKpbYjDHGJBVLbMYYY5KKJTZjjDFJxRKbMcaYpGKJLY6IyI/dWcQXuzPZfyaC+z6ptRm5RaRMRKI6/k5EfhTL4xlzKI/K1hMicnaLxx+IyE9aPH5MRL4oIl8XkUtbef9HZUVEykXkcy2e+7mIfDdSv0OysXFsccJdPuZMYJyqNohIDyDN47Ai5UfAb7wOwqQmD8vWWzizzjwpIoU4U9i1XCbqWOA6d+KEIynHmVU/FccTdpjV2OJHMbBLVRsAVHWXqm4VkfEi8ro70fJL7rIiiMgsEfmre/a5VEQmutsnisg77iTHb7eYZaRDjnDc37nrVK0SkePd7Vki8og463g9ISJzRKRCRG7Fmel+oYg84O7eLyK3u2fQL7uzOhgTLV6Vrbf5eDq1ScAzQJE4BgB1qrq9Ze3LjWmRiCwCrnO3pQG/AC5wY7rA3ecIN9a1IvI/Efu0koAltvjxMtDPTRb/EJETxZmz72/Aeao6HrgL+HWL92S5E7Re6z4HzpQ/x7uTHP+MTtSU2nHcgKpOBG4Abna3XQvsVdURwE+B8QCqehNOAS5X1Yvd1w4B/q6qI4F9wLkdjdGYDvCqbM0DRrmJaRLwDvABcJT7+O1W3nM38E1VHXtwg6o2usd72C1HD7tPDQc+izNH7c3u72Swpsi44S5mOB44HpgCPAz8ChgFvCLO1F1+nKVQDnrQfe9sEckTZ167XJxpgIbgLKvTmX/2YUc47sGJcecBZe79ycBf3XiWisjiw+x/naoubGUfxkScV2XLbfZchjPR+DHA74GBOEntaJymyo+4x8hX1dnupn/jTP7dlufcWmiDiFTiTPO3+XAxpQpLbHFEVUPALGCWiCzBaYpYpqrHtvWWVh7/EpipqueIs57WrE6EIkc4boP7M0Tn/ocaWtwPAdYUaaLKw7L1Fs7ivrmquldE3gWux0ls/+ro73GIQ8uRfZ+7rCkyTojIMPdM8KBynFnhi9yL34hIUERGtnjNBe72yTgLWu4HugFb3Ocv72Q4HxzhuK15Czjfff0IYHSL55qsmcR4xeOy9TbO5N2L3MeLcWpvpRyyGoi7NM4+95gAF7d4uhqnxmjawRJb/MjBaeZY7jbjjcBpVz8P+J17MXkhn1zbq15EFgD/BK50t/0e+K27vdUzOLdTR8vl3YeJyOaDN5yFMg933Nb8A+eLYjlOM88yYL/73HRgcYvOI8bEkpdl622c5sd3AFS1GWc17rmq2tpK1FcAfxdnZQVpsX0mTmeRlp1HTBtsdv8EJSKzgO+q6lyvYwEQZ2mPoKrWi8gg4FVgmHvh25iEEW9ly3SctcmaSMkCZrpNjgJca0nNGOMFq7EZY4xJKnaNzRhjTFKxxGaMMSapJMQ1th49emhZWZnXYRjTafPmzdulqkVex3GQlSmTDNoqVwmR2MrKypg71zoomcQlIhu8jqElK1MmGbRVrqwp0hhjTFKxxGaMMSapWGIzxhiTVCyxGWOMSSqW2IwxxiQVS2zGGGOSSlIktrKyEkSky7eyshKvfxVj4kJJaWlEylRJaanXv4pJQQkxju1INmzYglbe3OX9SM9bIhCNMdHlrqQwF9iiqmeKyADgIaAQZ0XyS7o6AfWWTZu4eebMLsd6y5QpXd6HMR2VFDU2Y1LMt3AWyjzod8CfVXUwsJeP1w8zJiVZYjMmgYhICXAGcIf7WICTgUfdl9wLnO1JcMbECUtsxiSWvwDfBw6uvlwI7HNXZgbYDPRt7Y0ico2IzBWRuTt37ox6oMZ4xRKbMQlCRM4EKlV1Xmfer6rTVbVCVSuKiuJmPmZjIi4pOo8YkyKOA74gIp8DMoA84K9AvogE3FpbCbDFwxiN8ZzV2IxJEKr6Q1UtUdUy4MvAa6p6MTATOM992WXAUx6FaExcsMRmTOL7AXCjiKzBueZ2p8fxGOMpa4o0JgGp6ixglnt/LTDRy3iMiSdWYzPGGJNULLEZY4xJKlFPbCLiF5EFIvKs+3iAiMwRkTUi8rCIpEU7BmOMMakjFjU2m/7HGGNMzEQ1sdn0P8YYY2It2jW2v2DT/xhjjImhqCU2m/7HGGOMF6I5js2m/zHGGBNzUaux2fQ/xhhjvODFODab/scYY0zUxGRKLZv+xxhjTKzYzCPGGGOSiiU2Y4wxScUSmzHGmKRiic0YY0xSscRmjDEmqVhiM8YYk1QssRljjEkqltiMMcYkFUtsxhhjkoolNmOMMUnFEpsxxpikYonNGGNMUrHEZowxJqlYYjPGGJNULLEZY4xJKpbYjDHGJBVLbMYYY5KKJTZjjDFJxRKbMcaYpGKJzRhjTFKxxGZMghCRDBF5T0QWicgyEbnF3T5AROaIyBoReVhE0ryO1RgvWWIzJnE0ACer6ligHDhNRI4Bfgf8WVUHA3uBK70L0RjvWWIzJkGoo8Z9GHRvCpwMPOpuvxc4O/bRGRM/LLEZk0BExC8iC4FK4BXgQ2Cfqja7L9kM9G3jvdeIyFwRmbtz586YxGuMFyyxGZNAVDWkquVACTARGN6B905X1QpVrSgqKopWiMZ4zhKbMQlIVfcBM4FjgXwRCbhPlQBbvIrLmHhgic2YBCEiRSKS797PBE4BVuAkuPPcl10GPOVJgMbEicCRX2KMiRPFwL0i4sc5KX1EVZ8VkeXAQyLyK2ABcKeXQRrjtaglNhHJAGYD6e5xHlXVm0VkAPAQUAjMAy5R1cZoxWEip6yshA0but7K1b9/X9av3xyBiFKLqi4Gjm5l+1qc623GGKJbYzs45qZGRILAmyLyAnAjzpibh0Tknzhjbm6LYhwmQjZs2IJW3tzl/UjPWyIQjTHGtC5q19hszI0xxhgvRLXziI25McYYE2tRTWw25sYYY0ysxaS7v425McYYEytRS2w25sYYY4wXotkr0sbcGGOMibmoJTYbc2OMMcYLNqWWMcaYpGKJzRhjTFKxxGaMMR1UUlqKiHT5VlJa6vWvkpRsEmRjjOmgLZs2cfPMmV3ezy1TpkQgGnMoq7EZY4xJKpbYjDHGJBVLbMYYY5KKJTZjjDFJpV2JTUSOa882Y0z7WJkyJnraW2P7Wzu3GWPax8qUMVFy2O7+InIsMAkoEpEbWzyVB/ijGZgxycjKlDHRd6RxbGlAjvu63Bbbq/h4hn5jTPtZmTImyg6b2FT1deB1EblHVTfEKCZjkpaVKWOir70zj6SLyHSgrOV7VPXkaARlkoQq0AjhevBlgqR5HVE8sTJlTJS0N7H9F/gncAcQil44JuFpGJpWQ8NiaNoAeuDj5yQLggM45xRAQyApfUnJypQxUdLexNasqrdFNRKT+BpXwYGXILwHJAeCgyDQEyQDtA6ad0LTWh7/f8DawVD0G8j9Moh4HbkXrEwZEyXtTWzPiMi1wBNAw8GNqronKlGZxKKNUPMsNC4Bfw/IOQ/ShrdeI9MwZ1/0S568vQC2XgRZd0DxfRDsG/u4vWVlypgoaW9iu8z9+b0W2xQYGNlwTMIJ7YXq/0BoN2SeBJmTD9/EKD6emgGUvQf77oDK78D6cujzEGRPjVHQccHKlDFR0q7EpqoDoh2ISUDNO6H636BNkHcJBDvwbyJ+6P41yDoRtpwHm06D4rug2yXRizeOWJkyJnraldhE5NLWtqvqfZENxySM0B6oute5n3c5BHp1bj/pw6H/W7DlHNh2qdOsmX9lxMKMV1amjIme9jZFTmhxPwOYCswHrBCmonANVN0PhCHvCggUdW1//m5Q8gJsORu2Xw2SCd0uikSk8czKlDFR0t6myG+2fCwi+cBD0QjIxDkNQfV/IVwNeZd1Pakd5EuHvo/Bps85NTdfDuR+ITL7jkNWpoyJns4uW3MAsGsEqah2BjRvhJzPQ7Aksvv2ZUHJM5BxtNNjsn5xZPcf36xMGRMh7b3G9gxOjy1wJmo9CngkWkGZ+HTOKUD9O5A+AdLHROcg/lzo+xRsqIDNX4Cy9yNXK4wjnSlTItIPp6myl/ve6ar6VxEpAB7GmcVkPXC+qu6NTuTGxL/2XmP7Q4v7zcAGVd0chXhMvGrazF2/AgJ9IfvU6B4r2Af6PgkbT4AtX4LSV0Ha+6+aMDpTppqB76jqfBHJBeaJyCvA5cAMVb1VRG4CbgJ+EI2gjUkE7WqKdCduXYkzG3l3oDGaQZk4owrbryYYAHK+GJskkzkRek+Hutdh1y+jf7wY60yZUtVtqjrfvV8NrAD6AmcBbhdV7gXOjkLIxiSM9q6gfT7wHvAl4HxgjojYEhupYv/dcOBFbvoT4C+I3XG7Xep0UNn9K6h9PXbHjYGulikRKQOOBuYAvVR1m/vUdpymytbec42IzBWRuTt37uxK+MbEtfZ2HvkxMEFVL1PVS4GJwE+jF5aJG02bofLbkHkif/+PB8fv/X+QNhi2XuzMbpI8Ol2mRCQHeAy4QVWrWj6nqsrH1+445LnpqlqhqhVFRcl33dKYg9rbpuRT1coWj3fT+R6VJpFU3ugMmi6+E9XBEdml3w/SgYmPy4+COQ/BY3/pwUXf/Xh7//59Wb8+YS/1dqpMiUgQJ6k9oKqPu5t3iEixqm4TkWKgsu09mHigquyuq4Pycn48YwbbampoCodJ9/vpk5tL39xcynv3prx3b9IDSXd9Oera+4m9KCIvAQ+6jy8Anj/cG6wHVxI4MMMZs9bjFkgbFLHdhkKglTd37E21s7nwjJlc+OULnAmWAel5S8Ri8kBnypQAdwIrVPVPLZ56GmfuyVvdn09FPlwTCVUNDby/dSvLKivZW18PZ5/N7956i145OWQEAtQ1NbHjwAHC6lS60/x+ji0p4ezhwzl7+HDK8vO9/QUSxGETm4gMxmm//56IfBGY7D71DvDAEfZtPbgSmTbCjm9CcCAUfN/raCDzOGhc4awikN/fWbg0AXWxTB0HXAIsEZGF7rYf4SS0R0TkSmADzjU7E0dqGhuZuX49C7dvR1UZ2L07x/Xrx7M33ED99u0EfB9X1kPhMFuqq3l/yxbe2byZlz78kG+/9BLffuklppSVcc348ZwzfLjV5A7jSJ/MX4AfArjNHo8DiMho97nPt/VG92L2Nvd+tYi07MF1kvuye4FZWGKLP3v+n5NISp4BX4bX0TiTJuecBftvh9qXIOdsryPqrL/Q+TL1JtBWG25KLY2QKFSVhdu389KHH9IUDjO+uJhJ/fqRn+GUqWd37vxEUgPw+3yUdutGabdunDtiBH8AVu/ezSPLlnHHggVc+NhjFGZm8vWKCv7nM5+hZ3a2B79ZfDtSYuulqksO3aiqS9xeWe3S2R5cwDUApaWl7T3UkWkjhPaBBMGXn6qLXB5e8y7Y/UvI/hzknOl1NB8L9HaWxambDWkjvI6msyJSpkz8awyFeHLlSlbs2kVZt26cMXQoPbKyOrWvIYWF/PiEE/jh8cczY+1abps7l9+88QZ/fOcdrjz6aL5z7LEM6N49wr9B4jpSYss/zHPtags6tAdXy04Dqqoi0mYPLmA6QEVFRauv6ZDmnVD7KjSt5qNOY5IDGRWQOclJdMax+9fORMc9/9frSD4t8wSnJnngebISszUy/zDPJcxvpKo0hEIEfT78PutHdqiqhgYeXLqUHTU1TBs4kEklJR3qMNUWnwinDBrEKYMG8cGuXfzv228zfd48/jl3LpeMHcvNJ55o1+E4cmKbKyJXq+rtLTeKyFXAvCPtPC56cKlC/dtQO9NJXhnHQqAYtAEaP4C6WdC4HHLOjWoYCaNxHez9O3S7AtLjsFYkfsg+E6ru5idf9zqYTulSmfKSqrJ2717mbdvGmj17aAqHEaAkL4+jioqoKC4m6D/MIrMpYueBA/x78WIaQiEuHDWKIYWFbb9YpOsJLzeX7M9+lgd9Ph5YvJirx43jxyecQJ/c3K7tN4EdKbHdADwhIhfzcaGrANKAcw73xrjowaXq1NLq34a0oyD7DPC1aI/OGA+Na6DmSai6i6Pj8Hs85nb9xJlZpEcc9zgMlkJ6Od+5fCE0rID0o7yOqCNuoJNlyks1jY08t2oVK3fvJisYZGzv3hRkZFDb1MSHe/fy8ocfMmfzZs4YMuTwX+RJbndtLfcuWoSIcEV5Ob1zcg7/BlVunjmzy8e9ZcoUNt95J7+aPZvp8+dz18KFXD9hAj+YPLnTzZ+J7LCJTVV3AJNEZAowyt38nKq+1o59e9+Dq262k9TSK5zrRa2dGaUNhm5XQ9XdvHJnAzQsj8+aSizUz4eq/0DhjyDY1+toDi9rGgcqF/LmgyOYekXndxPrsXBdLFOeOFgDqW1qYtrAgXymb99PdHiYCqzft48X1qzhP0uXMqWsjONLSyPS9JZI9tbVce+iRQBcNnZszBNK37w8bjvzTL533HH8fNYs/vjOO/xr3jx+OHky3z72WDJSqBdle9djmwl06LTC8x5cjaudZsa0MW0ntYP83SDvUpp2/A22fBH6v+/MMp9qKn8A/sL46N5/JL5sfvhn+OfPQTd9EdJHd2o3Xo2F60yZ8sKOmhruW7wYAa4aN67NGkhZfj5XHX00z6xaxcz166lrauLUQZEb+xjvapua+PfixTSHw54ktZYGdu/Ofeecw02TJ/PDGTP40Wuv8a958/jt1Kl8edSolDjhSM6rvuFqqHkc/L2cXn3t+UP6C7jwuzgJccfXnGbMVHJgltNsW/gTJ9EngNv/C/j7wIGXnWumJqJqGhv5z9Kl+NvZrBb0+zln+HAm9u3Lu1u2MGv9+tgE6rFQOMwjy5ZR1dDARaNH0+tIzY/R4F6ra3kb2bMnT194IdxzDxtWruSixx/Hd801iFubbu1WEske6B5KvrqpKtQ8D9oMuV/qUG/HWe/hXFva9VNnFvu8FJnnWRV23QyBPpD/Na+jabdwGMg+HaruhLo3IcuGckWM389DS5dS19TEFeXlFLazBiIinDZoEI2hELM3boRRo478pgSmqjy7ejUb9u/ni0cdRUlenleBHPZaXViVxTt28FpaGtVXXsnIoiKmDRz40Xi6g26ZMiXakcZE8tXYGldA00rIOslpVuuowpsg/WjYcT2EUmSmr9qZzvXIwh8m3owewRKnubnundT5e8XCSSexpbqas4cPp7iDvetEhDOHDKG0Wzc46ywWbt8epSC9N3fbNhZu384J/fszumdPr8Npk0+E8t69uX7iRE7s359Vu3fz9/ff540NG2gOh70OL+KSK7FpkzMrhb+3062/MyQAxXdAaBfs/GFk44tHH9XW+kK3q7yOpnOypgI+pynVdNnsDRtg8mTGFRczopOrAPh9Pr40YgTU1XHhY49R19QU4Si9t72mhpfWrGFIQQEn9e/vdTjtkub3c1JZGddPnMjQggJeW7+ef86dy9q9yXVSmFyJrf5dCFdB9mdBuvCrZYyD7tfDvtuh/lOTRCSX2hlOM17hj+Jj6qzO8Oe5c0kuh6b1XkeT8H79xhuwZw+f7WLnj5y0NHjySVbu2sUPZ8yIUHRxIi2N/y5fTlYwyNnDhydch4y89HS+NHIkF40aRViVfy9ezGMrVoAX1wejIHkSW/iA8wUdHAbBsq7vr8fPwNcNdn73yK+Nc2VlJW1eLH7rqVPYuBXSe13X5msO3uJa5iTn73XgJdDka1qJpScuuAAeeIC0SAy2XruW6ydM4K9z5jBj7dqu7y8OqCqceSZ76+o496ijyAom7qxFQwoL+UZFBSf078+KnTvh2mt5aOlS53dMYMnTeaTuLacpMntaZPbnL3CSW+W3nV532adGZr8e2LBhS+vLxDR+CNX3Q/YZNGypOOJ+4nqZGAlC1jSoeQwaFjq1btMpWcEg7NkTsf397pRTeGXtWq546imWX3edU5NLYPctWgRjxnBSWRn9k2D6qqDfz5SyMkYVFfGPJ5/kwsce49Hly/nHGWck7ATLSVFjK8wH6udC2ijw94jcjrtfC4FS2Pmz5Ov+r+qM8/N1czrLJIO0kRDoB7WvQdi6/8eLrGCQu886i01VVfx81iyvw+mSzVVVfOvFF2H9eiYnSdf4g4qys+Guu/jt1Kk8s2oVI//xD55audLrsDolKRLbty8DaILM4yO7Y0mDHj+G+jlw4MXI7ttrTR9C82bnM5Mkmd9PBLJPAz3g9PI0cePYfv24etw4/vLuuyxK0F6SqsrXnn2WxlAInnoKX7w3z3dGOMxNkycz75prKO3WjbMffpgbXnzR+Z0TSOInttBevvkVnGVMAp3rwXVY3S6HQH+n52Cy1No+UVsr9zqayAr0cX6n+jnW/T/O3DptGt0zM/n6c899tEJ0Irlv0SKeX72aW6dNgyTrRfgR93r66F69mH/ttfDuu/x1zhzSv/ENpKDgiNfh42Wgd+JfY9v7/8jLwVnOJBokDXr8FLZfBQeeh5wzonOcWGpaA81bnFnyk6W21lLWydCwzOn+n/slr6MxroLMTP546qlc9uST3Dl/PlePH+91SO22xW2CPL60lOsnTuRbXgcULa0M9F6xcydP+f1w442cPXw4w3sc+XKP1wO9E7/G1rCEJ18FAq2uVxoZ3S6F4ADY9YvEr7WpQt3ryVlbO8iX26L7/wavozEtXDJmDMeXlvLDGTPYU1fndTjt0rIJ8q6zzkrOJsjDOKqoiK+NH09hVhYPL1vG7A0b4r7XZOIntr6POnM8RpMEnYmB699L/Gs3TR86tbVkurbWmsxJ4Mtzu//HdyFMJSLC/33uc+ytr+cnr8Xtggaf8O/Fi3lu9Wp+O3UqgwsKvA7HE90zM7l87FhG9+zJzPXreXzFCpri+Lpb4ic2oD4WHeC6XQb+nrD7dzE4WJSkQm3tIAk6M5KEtkHjYq+jMS2M6dWL6yZM4J9z5zJ/2zavwzmsrdXVfOvFF5lcWso3P/MZr8Px1MFJrqcOGMDSnTu5Z9EiDjQ2tv7idl6Li9Z1usS/xhYrvkzo/j/OQpz1iyFjjNcRdVzTWqcnZPYZyV1bOyhtNATegwMznIVmJbHHTyWTX0yZwsPLlnHd88/z1le/GpfNewebIOubm7nrC1+IyxhjTUSYXFpKUVYWj65YwV0LF/KV0aPpnnnIHLMRWEC1K9fpkqLGFjPdrwVfDuz5vdeRdNxHPSHzkmfc2pGIQNZnQauh7m2vozEt5Gdk8Ltp03h382ZnwHMcemDJEp5dtYrfnHxySq8K3pphPXpw6Zgx1DY1cdfChWyvqfE6pE+wxNYR/u7Q7RqoeijxOiUcrK0l+7W1QwX7OQO3696CUJXX0ZgWLh07lmNLSvj+K6+wr77e63A+YVt1Nf/zwgtM6teP/0nxJsi29OvWja+Wl+MT4Z6FC9m0f7/XIX3EEltHFdwACOz5k9eRdEzd625trdzrSGIvaxqgzoTPJm743I4ku2pr+VkXm60iSVX5+nPPUec2Qfp99jXZlqLsbL5aXk52Whr3L1nCxjhJbvYX66hgP8i7GPbdAaHdXkfTLlOPBZo3QeZkZ1meVOPPh4xjnE4kzVu8jsa0MK64mK9XVPD3999n8Y4dXocDwH+WLOHpDz7gV1OmMKwdY7ZSXbeMDC4fO5bctDTuX7yY9fv2eR2SJbZOKfweaC3s/T+vIzkyVW6+FmdsV6pcW2tN5vEg2db9Pw796uST6Z6RwXXPP+/5+Kit1dVc/8ILHFtSwg3HHONpLIkkNz2dy8aOpVtGBg8sWQIer09nia0z0kc6s3bs/ZuzXE48q32N4ytI3draQb50yJri1Fwbl3sdjWmhIDOT306dypsbNzpfih5RVa56+mkampu55+yzrQmygw4mt/yMDLjoIrZVV3sWi/3lOqvwJqcpct+dXkfSNlXY9VM2bwfSbRkX0o8Gfy9nqi1t9joa08KV48YxoU8fvvfKK1Q1eLMywx3z5/PCmjX8bto0hlovyE7JSUvjkjFjoK6O+5csYVdtrSdxWGLrrKzjnOatPX9w1oGLRzXPQt07/OIfpHZt7SDxOevqhfc5q62buOET4e+f+xw7amq4xYOlbdbt3cuNL7/MlLIyrps4MebHTyZ56elw330Izqwt+z3o8WqJrSsKb3Katqoe9DqST9Mw7PoxBAdz9xNeBxNHggMhOBTq3oBwfI29SXUT+vblyqOP5q9z5rCssjJmxw2Fw1z+1FMIpORckFGxZw9fGTOGhuZm/r14cdszlESJJbauyD4d0kc702xp2OtoPqnqQWhYAkW/pNla3T4p+1SnKbI2frqYG8dvp00jLz2d6194IWYdSX41ezazN2zg/51+OmVJsCJ2vOidk8NFo0ezv6GBB5cujenckpbYukIECm5yOiPUPOt1NB/TRtj1M2fMWu75XkcTf/yFkDEBGhYweqjXwZiWemRl8euTT2bW+vXcvXBh1I/3+vr1/GL2bC4ZM4bLxo6N+vFSTWm3bpx71FFsqa7miZUrY3ayYomtq/LOh2AZ7P5t/HQj33enM9NI0a+d60rm0zJPBMngbz8hfv5u7SAid4lIpYgsbbGtQEReEZHV7s/uXsbYVdeMH89JZWX8zwsvsGbPnqgdp/LAAS56/HEGFxTwjzPOQKwJMiqG9+jBqYMGsWLXLl5ZuzYmx7Rvva6SABR8z+mMUPeG19FAqBp23eJ0788+3eto4pcvE7KmcuIEoOoBr6PpiHuA0w7ZdhMwQ1WHADPcxwnL7/Nx39lnk+b3c/Hjj0elCauhuZlzH3mEPXV1PHzeeeSk2QTZ0XRM375M6NOHdzZvZu7WrVE/XtQSWyqcWX6k2xXukja/8ToS2PNbCO2Ann90mkpN29LHMWcRUPldCO3zOpp2UdXZwKHVmLOAe9379wJnxzKmaOjXrRv/OvNM3tuyJeLTbakq33juOd7cuJF7zz6b8t69I7p/82kiwmmDBzOkoIDnV6+Oak0coltju4ckP7P8iC8TCr7jzGpR6+Es8o3rnTks874CmdZl+YhEuPYXQKjSuSaZuHqp6sGFzbYDrS4nLyLXiMhcEZm7c+fO2EXXSV8aOZKrx43j1rfe4uGlS4/8hnYoKS3FN3myc/1u1iwuGDWqU2uFmY7ziXDeiBH0zM7m0eXLozrGLWqDm1R1toiUHbL5LOAk9/69wCzgB9GKIaa6X+cklV0/hVKPJtvd+QPAB0W/9eb4CWj+ciD/G7D3707NOyOxpx1TVRWRVi8aqup0YDpARUVFQlxY/Nvpp7N8506ueOopyvLz+UxJSZf2t6VnTzj1VEYWFXHuz36G3Hxzp/bTlbXCUlma38+XR43i9vnzeWjpUq4aN46MQOTTUKyvsbXrzBIS7+wSXzYU/ghqX4MDHix5Xzsbqh+Bgu9DsGuFP+UU/Qr8PWD7N+Jv2Eb77BCRYgD3Z+wGgUVZeiDA4xdcQJ/cXE574AEWdGHF7X/NnQtnnsmQggLOGT7cal4eyc/I4PwRI9hbX89jy5cTjkLnLc86j6jT77PN30hVp6tqhapWFBUVxTCyLsi/BgIlTq0tlj3twg2w/WtO78zC78fuuMnC3x16/i/Uz4H9cTxFWtueBi5z718GPOVhLBHXMzubGZdeSl56OlPvu4/X16/v0PvDqvz0tdf4+nPPwerVfGnECJsH0mP98/P53ODBrNm7lxlR6CkZ679u0p5ZAuDLgB4/dVZrrnk6dsfd87/QuBJ6/QN8WbE7bjLJu8QZAlD5PWiKfq+tzhKRB4F3gGEisllErgRuBU4RkdXANPdxfOjE9avWbseNGcOsyy6jV04Op/z73/zfe++160x/W3U1p91/P7964w2uKC+Hhx4i6E+hhXbj2Pg+fajo04e3N2+O+JJFsZ5A8OCZ5a0k4Zkl4Fyn2fNXqLwRsj/rJLtoalwDu38FuV+CHOve32kiUHw7rBsDO66Fvk/EZa9SVb2wjaemxjSQ9lLl5gj0arxlyhQGdO/O21/9Khc9/jjffOEFHlm2jFtOOomTyso+1ay4q7aWf82dy61vvUVzOMz0M8/kqnHjuDuckE3NSeu0QYPYdeAAT3/wAYWZmfTNy4vIfqOW2Nwzy5OAHiKyGbgZJ6E94p5lbgCSb1oMCUKvv8KmU5zOJD1+FL1jaQi2XQWSDj3/Er3jpIq0IdDjF7Dz+1D9X2fwvYkr3TMzef6ii7hn4UJ+8OqrnHzffQwuKOD40lJ65+TQ0NzM4spKXl+/nqZwmHOGD+d306YxxGbrj0t+n48vjRzJ7fPn8/CyZVw9bhy56eld3m80e0Um1pllJGVPg5xzYPevodul0evMseePUPc69L4Tgn2ic4xUU/BtqH4YdlwP2VOd6bdMXBERrjj6aL48ahQPuKtdP7NqFfvq6/GLMLJnT745cSKXl5czuleb/dNMnMgKBvnyyJHcuWABjyxfzmVjxxLo4jVQW8skWnr+EdY9D5Xfhr7/jfz+6+fDzp9Azhed5k8TGRKA3nfB+vGw41vQ536vIzJtyAwGuWrcOK4aZ2sNJrpeOTmcPXw4/12+nOdXr+bzQ7s2iat1DYqWtAFQ+DOofhSqHo7svsM1sPUrEOgBxdPj8lpQQssYA4U/dqbaqnrE62iMSQkjioqYXFrKgu3bmduFYR1giS26Cr8PGRNh+7WR62mnCtuugMYPoPg+ayqLlh4/dv92X4emzV5HY0xKmFJWxpCCAl5cswZKSzu9H0ts0SQBKL4XtB62nu8sJ9NVu3/l1AKLfudcyzPRIUGnGVIbYdvliTpw25iE4hPhi0cdRfeMDDj/fDbt39+5/UQ4LnOo9OFQfCfUvQU7vt21gdt7/+XMaZh3qTM3pYmutCHQ6y9QOwP2/sXraIxJCRmBABeMHAm1teypq+vUPiyxxULel6Hgu7DvH7D7l53bx747Ycc3IPsMKL7DrqvFSrcrIecs2PlDqJvrdTTGpISi7Gy47TbGdnLlBUtssVL0O+h2Oey6GXbe3P6mLQ3Drl/C9qsg+1Snh6UEoxqqaUHEqXH7e8OW8yC02+uIjEkNXWjdssQWK+KD3nc4yW33L2DLl6B51+Hf07QFNp/uNj9+BUqedpbIMbHlL4S+j0Jom9Mb1a63GRPXLLHFkvidMVJFf4Cap2DtENh96yd73alCw1Jn8cu1g51Z+3vd5vSAFFvl1zOZE6DnX+HAi04HHmNM3LLE1oLfT0QmbC0rO8xMIyJQ+B0YsAgyJjjXbj7sB2v6wrrRsKan83PPn3jsFWHgtHqk4BuIz9fpeEzbOvQ3L/gG9z0F4cqbOXNKB/7mxpiYsplHWgiFQCs7t/BgS9LzliO/KH0klL7sTGJc/ZgzLi20BzInQfrRkHsW5x3VJ3bxpKgO/821CfbfzbO37XJmfAkUA/YZGxNPLLF5LW0wFCbHIuIpQYKQd6GzblvVf6DbVeDv5nVUxpgWrCnSmI7y5ULuRUATVP/HWejVGBM3LLEZ0xmBnpDzJQjtguqHSbd+PcbEDUtsxnRW2iBn8HbzOh75M871N2OM5yyxGdMV6WMg+3N8djJQP8/raIwxWGIzpusyJjD0dCDzGK8jMcZgic2YiNgYoVWJjDFdZ4nNGGNMUrHEZowxJqlYYjPGGJNULLEZY4xJKpbYjDHGJBVLbMYYY5KKJTZjjDFJxRKbMcaYpGKJzRhjTFKxxGaMMSapWGIzxhiTVDxJbCJymoh8ICJrROQmL2IwJplYmTLmYzFPbCLiB/4OnA6MAC4UkRGxjsOYZGFlyphP8qLGNhFYo6prVbUReAg4y4M4jEkWVqaMaUFUNbYHFDkPOE1Vr3IfXwJ8RlWvP+R11wDXuA+HAR/ENNC29QB2eR1ElNjvFj39VbUoGjvuQpnaTfL+vTvD6/+ReJIon0Wr5SrgRSTtoarTgelex3EoEZmrqhVexxEN9rslt0PLlH0mn2Sfx8cS/bPwoilyC9CvxeMSd5sxpnOsTBnTgheJ7X1giIgMEJE04MvA0x7EYUyysDJlTAsxb4pU1WYRuR54CfADd6nqsljH0QVx1zwaQfa7JaAulKmk/Uw6yT6PjyX0ZxHzziPGGGNMNNnMI8YYY5KKJTZjjDFJxRJbO4lIPxGZKSLLRWSZiHzL65giSUT8IrJARJ71OpZIEpF8EXlURFaKyAoROdbrmOKBTcH1MRG5S0QqRWSp17F4KZm+4+waWzuJSDFQrKrzRSQXmAecrarLPQ4tIkTkRqACyFPVM72OJ1JE5F7gDVW9w+0xmKWq+zwOy1PuFFyrgFOAzTi9Ki9Mlv/ljhKRE4Aa4D5VHeV1PF5Jpu84q7G1k6puU9X57v1qYAXQ19uoIkNESoAzgDu8jiWSRKQbcAJwJ4CqNqZ6UnPZFFwtqOpsYI/XcXgtmb7jLLF1goiUAUcDczwOJVL+AnwfCHscR6QNAHYCd7vNrHeISLbXQcWBvsCmFo83k6BfYCY6Ev07zhJbB4lIDvAYcIOqVnkdT1eJyJlAparO8zqWKAgA44DbVPVo4ACQ0teTjDmSZPiOs8TWASISxPmDP6Cqj3sdT4QcB3xBRNbjNEmdLCL3extSxGwGNqvqwbPOR3ESXaqzKbhMq5LlO84SWzuJiOBcq1mhqn/yOp5IUdUfqmqJqpbhTMX0mqp+xeOwIkJVtwObRGSYu2kqkHAXwqPApuAyn5JM33GW2NrvOOASnBrNQvf2Oa+DMkf0TeABEVkMlAO/8TYc76lqM3BwCq4VwCMJNq1dRInIg8A7wDAR2SwiV3odk0eS5jvOuvsbY4xJKlZjM8YYk1QssRljjEkqltiMMcYkFUtsxhhjkoolNmOMMUnFElucEZGQ2812qYj8V0SyDvPa8vZ0xxWRk1qbtV9EyqI9o7mI/CiWxzOmLTEuW0+IyNktHn8gIj9p8fgxEfmiiHxdRC5t5f0flZVDYxGRn4vId48UWyqzxBZ/6lS13J1lvBH4+mFeWw7E+ziTHx35JcbERCzL1lvAJAARKcSZzq3lkknHAm+r6j9V9b4j7KursaQcS2zx7Q1gsIhku2tGvedO5nuWO2PEL4AL3LPQC0Rkooi8477m7RYzbnSIiIwXkddFZJ6IvOQuZ4GIzBKR37lxrBKR493tWSLyiLuO0xMiMkdEKkTkViDTje8Bd/d+EbndXe/pZRHJjMDnZExHRbtsvY2b2NyfzwBF4hiAk2S3t6x9ueVukYgsAq5zt30qFnefI9zyuFZE/iein0wSsMQWp0QkAJwOLAF+jDPV1URgCvC/QBD4GfCwexb6MLASON6d8PdndGKWDXeuuL8B56nqeOAu4NctXhJw47gBuNnddi2wV1VHAD8FxgOo6k18fJZ8sfvaIcDfVXUksA84t6MxGtMVMSpb84BRbmKahDOzyQfAUe7jt1t5z93AN1V17MEN7rJCh8YCMBz4LM4SRDe75da4Al4HYD4lU0QWuvffwJm77W2ciYoPtqtnAKWtvLcbcK+IDAEUp4B21DBgFPCKM3UcfmBbi+cPTow6Dyhz708G/gqgqkvd6avask5VF7ayD2OiLWZlS1UbRGQZzqTbxwC/BwbiJLWjcZoqPyIi+UC+uzYcwL9xkm9bnlPVBqBBRCqBXjiTfhssscWjOlUtb7lBnAxzrqp+cMj2zxzy3l8CM1X1HHHWU5rVieMLsExVj23j+Qb3Z4jO/f80tLgfAqwp0sRKrMvWWzgL3eaq6l4ReRdnjs6jgX916jf42KHlyL7LW7CmyMTwEvBNtxAiIke726uB3Bav68bHy49c3sljfYBzLeBY91hBERl5hPe8BZzvvn4EMLrFc03WTGLiWDTL1tvA14BF7uPFOLW3UuATvYPdld33ichkd9PFLZ4+NBZzBJbYEsMvcZo+FrvNG790t8/EuYh88KLy74HfisgC2jiDczt13NFi08EZzTeLyGbgLOA84HfuReyFfHwRvC3/wEmGy4FfAcuA/e5z0924H2jrzcZ4KJpl622c5sd34KNVFSqBuara2mr1VwB/d5tLpcX2Q2MxR2Cz+5suExE/EFTVehEZBLwKDHMvfBtjTExZu6yJhCxgptvkKMC1ltSMMV6xGpsxxpikYtfYjDHGJBVLbMYYY5KKJTZjjDFJxRKbMcaYpGKJzRhjTFL5/23DCqVAwBZ7AAAAAElFTkSuQmCC",
      "text/plain": [
       "<Figure size 504x504 with 4 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "fig, axs = plt.subplots(2, 2, figsize=(7, 7))\n",
    "\n",
    "sns.histplot(data=df_iris, x=\"Sepal.Length\", kde=True, color=\"skyblue\", ax=axs[0, 0])\n",
    "sns.histplot(data=df_iris, x=\"Sepal.Width\", kde=True, color=\"olive\", ax=axs[0, 1])\n",
    "sns.histplot(data=df_iris, x=\"Petal.Length\", kde=True, color=\"gold\", ax=axs[1, 0])\n",
    "sns.histplot(data=df_iris, x=\"Petal.Width\", kde=True, color=\"teal\", ax=axs[1, 1])\n",
    "\n",
    "plt.show()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "\n",
    "\n",
    "### 사분위수(Quartile)\n",
    "\n",
    "데이터를 정렬하면 최소값(Min), 최대값(Max), 범위(Range)를 알 수 있으며 대표 값 중에 하나인 중앙값(Median)을 통해 데이터 범위 내에 주요 데이터들의 위치를 알 수 있습니다.\n",
    "\n",
    "데이터의 분포를 파악하기 위해 데이터를 4등분하여 보는 것은 의미가 있기 때문에 데이터를 4등분하여 나타낸 것을 사분위수(Quartile)라고 합니다. 여기서 각 4등분 위치를 1사분위수(Q1), 2사분위수(Q2=중앙값), 3사분위수(Q3)로 나타내며 1사분위수에서 3사분위수까지를 사분범위(Interquartile Range)라고 합니다. \n",
    "\n",
    "숫자로는 직관적으로 분포를 파악하기 힘들기 때문에 상자수염그림(Boxplot)을 사용하여 시각화하여 판단합니다. \n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 38,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Q1: 2.8, Q2: 3.0, Q3: 3.3, IQR: 0.50\n"
     ]
    }
   ],
   "source": [
    "# 사분위수 \n",
    "q1 = df_iris['Sepal.Width'].quantile(.25)\n",
    "q2 = df_iris['Sepal.Width'].quantile(.5)\n",
    "q3 = df_iris['Sepal.Width'].quantile(.75)\n",
    "iqr = q3 - q1\n",
    "print(f\"Q1: {q1}, Q2: {q2}, Q3: {q3}, IQR: {iqr:.2f}\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 39,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Text(0.5, 1.0, '')"
      ]
     },
     "execution_count": 39,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD7CAYAAAB68m/qAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAQZUlEQVR4nO3df4ylVX3H8ffHXRSKCAmQKQF02mjs4DaCTCgo2lmIrQLBtmKA1B+YMWtbRbQaszgNVtqp4B9qW20tcdqstplg/BWEWjVxbi2imFkFBEYNaTBANQgIshS37vrtH/PQDsvMzp3dmZ2Zs+9XcsO9z3Puc75LZj9z9jzn3pOqQpK0/j1ttQuQJC0PA12SGmGgS1IjDHRJaoSBLkmNMNAlqRF9B3qSDUm+k+T6ec5dkuQnSW7pHm9a3jIlSYvZuIS2lwEzwLMWOH9tVb11/0uSJO2LvgI9yQnAucA48KfL0fExxxxTg4ODy3Epadk99thjHH744atdhvQU27dvf6Cqjp3vXL8j9A8D7waO2EubVyd5GfAD4B1Vdc/eLjg4OMj09HSf3UsHVq/XY2RkZLXLkJ4iyQ8XOrdooCc5D7i/qrYnGVmg2ReAyarameTNwDbgrHmutQXYAjAwMECv11u0eGk17Nixw59PrTtZ7LtckrwfeB2wCziU2Tn0z1bVaxdovwF4qKqO3Nt1h4eHyxG61ipH6FqrkmyvquH5zi26yqWqLq+qE6pqELgI+OqeYZ7kuDkvz2f25qkk6QBayiqXJ0lyJTBdVdcBb0tyPrOj+IeAS5anPElSv5YU6FXVA3rd8yvmHL8cuHw5C5MkLY2fFJXmmJycZNOmTZx99tls2rSJycnJ1S5J6ts+T7lIrZmcnGRsbIyJiQl2797Nhg0bGB0dBeDiiy9e5eqkxTlClzrj4+NMTEywefNmNm7cyObNm5mYmGB8fHy1S5P6YqBLnZmZGc4888wnHTvzzDOZmXHRltYHA13qDA0NceONNz7p2I033sjQ0NAqVSQtjYEudcbGxhgdHWVqaopdu3YxNTXF6OgoY2Njq12a1BdvikqdJ258XnrppczMzDA0NMT4+Lg3RLVuLPrR/5XiR/+1lvnRf61V+/XRf0nS+mCgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtzuMGF1jO/y0XquMGF1jtH6FLHDS603hnoUscNLrTeGehSxw0utN4Z6FLHDS603nlTVOq4wYXWOze4kObhBhdaq9zgQuqT69C1njnlInVch671zhG61HEdutY7A13quA5d652BLnVch671zkCXOq5D13rnTVGp4zp0rXd9r0NPsgGYBu6rqvP2OPcM4BPAqcCDwIVVdfferuc6dK1lrkPXWrVc69AvAxa6OzQK/LSqngt8CLh6aSVKkvZXX4Ge5ATgXODjCzR5FbCte/5p4Owk2f/yJEn96neE/mHg3cAvFzh/PHAPQFXtAh4Bjt7f4iRJ/Vv0pmiS84D7q2p7kpH96SzJFmALwMDAAL1eb38uJ/Vl8+bNB6SfqampA9KPtJB+Vrm8BDg/yTnAocCzkvxzVb12Tpv7gBOBe5NsBI5k9ubok1TVNcA1MHtT1JtOOhD25QvoBrfewN1XnbsC1UgrZ9Epl6q6vKpOqKpB4CLgq3uEOcB1wBu65xd0bVbnaxwl6SC1z+vQk1wJTFfVdcAE8MkkdwEPMRv8kqQDaEmBXlU9oNc9v2LO8Z8Dr1nOwiRJS+NH/yWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqRGLBnqSQ5N8K8mtSe5I8r552lyS5CdJbukeb1qZciVJC9nYR5udwFlVtSPJIcCNSb5YVd/co921VfXW5S9RktSPRQO9qgrY0b08pHvUShYlSVq6fkboJNkAbAeeC3y0qm6ep9mrk7wM+AHwjqq6Z57rbAG2AAwMDNDr9fa1bmnF+fOp9SazA/A+GydHAZ8DLq2q2+ccPxrYUVU7k7wZuLCqztrbtYaHh2t6enrfqpZW2ODWG7j7qnNXuwzpKZJsr6rh+c4taZVLVT0MTAGv2OP4g1W1s3v5ceDUfahTkrQf+lnlcmw3MifJYcDLge/t0ea4OS/PB2aWsUZJUh/6mUM/DtjWzaM/DfhUVV2f5EpguqquA96W5HxgF/AQcMlKFSxJml8/q1xuA06Z5/gVc55fDly+vKVJkpbCT4pKUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmN6GuDC2mteOH7vswjj//igPQ1uPWGFb3+kYcdwq3v/Z0V7UMHFwNd68ojj//igGw80ev1GBkZWdE+VvoXhg4+TrlIUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjVg00JMcmuRbSW5NckeS983T5hlJrk1yV5KbkwyuSLWSpAX1M0LfCZxVVS8ETgZekeT0PdqMAj+tqucCHwKuXtYqJUmLWjTQa9aO7uUh3aP2aPYqYFv3/NPA2UmybFVKkhbV1xx6kg1JbgHuB75SVTfv0eR44B6AqtoFPAIcvYx1SpIWsbGfRlW1Gzg5yVHA55Jsqqrbl9pZki3AFoCBgQF6vd5SL6GD3BFDW/nNbVsPTGfbFm+yP44Ygl7v8JXtRAeVvgL9CVX1cJIp4BXA3EC/DzgRuDfJRuBI4MF53n8NcA3A8PBwjYyM7GPZOlg9uvUq7r7q3BXvp9frsdI/n4Nbb2DkDSvbhw4u/axyObYbmZPkMODlwPf2aHYd8Ibu+QXAV6tqz3l2SdIK6meEfhywLckGZn8BfKqqrk9yJTBdVdcBE8Ank9wFPARctGIVS5LmtWigV9VtwCnzHL9izvOfA69Z3tIkSUvhJ0UlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGLOnrc6W1YHDrDQemo39b2X6OPOyQFb2+Dj4GutaVA/Fd6DD7S+NA9SUtF6dcJKkRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYsGuhJTkwyleTOJHckuWyeNiNJHklyS/e4YmXKlSQtpJ9NoncB76yqbyc5Atie5CtVdece7f6jqs5b/hIlSf1YdIReVT+qqm93zx8FZoDjV7owSdLSLGkOPckgcApw8zynz0hya5IvJnnBchQnSepfP1MuACR5JvAZ4O1V9bM9Tn8beE5V7UhyDvB54HnzXGMLsAVgYGCAXq+3j2VLK8+fT603qarFGyWHANcDX6qqD/bR/m5guKoeWKjN8PBwTU9PL6FU6cAZ3HoDd1917mqXIT1Fku1VNTzfuX5WuQSYAGYWCvMkv9q1I8lp3XUf3PeSJUlL1c+Uy0uA1wHfTXJLd+w9wLMBqupjwAXAHyfZBTwOXFT9DP0lSctm0UCvqhuBLNLmI8BHlqsoSdLS+UlRSWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqRH9bBItrWvJXrfEXfh9Vy+tvfuia7U5QlfzqmrJj6mpqSW/R1ptBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktSIRQM9yYlJppLcmeSOJJfN0yZJ/ibJXUluS/KilSlXkrSQfkbou4B3VtVJwOnAW5KctEebVwLP6x5bgL9f1iqlA2RycpJNmzZx9tlns2nTJiYnJ1e7JKlvi359blX9CPhR9/zRJDPA8cCdc5q9CvhEzX7l3DeTHJXkuO690rowOTnJ2NgYExMT7N69mw0bNjA6OgrAxRdfvMrVSYtb0hx6kkHgFODmPU4dD9wz5/W93TFp3RgfH2diYoLNmzezceNGNm/ezMTEBOPj46tdmtSXvje4SPJM4DPA26vqZ/vSWZItzE7JMDAwQK/X25fLSCtiZmaG3bt30+v12LFjB71ej927dzMzM+PPqtaFvgI9ySHMhvm/VNVn52lyH3DinNcndMeepKquAa4BGB4erpGRkaXWK62YoaEhNmzYwMjICL1ej5GREaamphgaGsKfVa0H/axyCTABzFTVBxdodh3w+m61y+nAI86fa70ZGxtjdHSUqakpdu3axdTUFKOjo4yNja12aVJf+hmhvwR4HfDdJLd0x94DPBugqj4G/CtwDnAX8N/AG5e9UmmFPXHj89JLL2VmZoahoSHGx8e9Iap1I6u1F+Lw8HBNT0+vSt/SYp6YcpHWmiTbq2p4vnN+UlSSGmGgS1IjDHRJaoSBLkmNMNAlqRGrtsolyU+AH65K59LijgEeWO0ipHk8p6qOne/EqgW6tJYlmV5oaZi0VjnlIkmNMNAlqREGujS/a1a7AGmpnEOXpEY4QpekRhjoWvOSjHUblN+W5JYkv7WM1x5Jcv08xz+X5PfmvP5+kj+b8/ozSf4gyR8lef087x9Mcnv3/OQk58w59+dJ3rVcfwbpCX3vWCSthiRnAOcBL6qqnUmOAZ5+ALr+OvBi4PNJjgYeA86Yc/4M4C1V9eM+rnUyMMzs10xLK8YRuta644AHqmonQFU9UFX/leTUJP+eZHuSLyU5DiBJL8lfdyP525Oc1h0/Lck3knwnyU1Jnr9IvzcxG+h0//0CcGy3icuvAY9X1Y/njra7mm5Ncivwlu7Y04ErgQu7mi7srnlSV+t/Jnnbsv3f0kHNQNda92XgxCQ/SPJ3SX672xLxb4ELqupU4B+BuTs5/0pVnQz8SXcO4HvAS6vqFOAK4K8W6Xc7sKkL5BcD3wC+Dwx1r2+a5z3/BFxaVS984kBV/U/X37VVdXJVXdud+g3gd4HTgPd2fyZpvzjlojWtqnYkORV4KbAZuBb4S2AT8JXZHRLZAMzd8nCye+/XkjwryVHAEcC2JM8DCthrgHbTO3cALwJOBz4A/DqzYX4Ks1My/6fr46iq+lp36JPAK/fSxQ3dvzp2JrkfGADu3VtN0mIMdK15VbUb6AG9JN9ldjrjjqo6Y6G3zPP6L4Cpqvr9JIPd9RbzdeBlwBFV9dMk3wTeymyg/8NS/xx72Dnn+W78u6hl4JSL1rQkz+9G1U84GZhhdj77jK7NIUleMKfNhd3xM5ndsPwR4Ejgvu78JX12fxPwZuDW7vVtzI7Wnw3cPrdhVT0MPNz1CfCHc04/yuy/EKQVZaBrrXsms1Mldya5DTiJ2TnpC4CruxuQt/D/NzABfp7kO8DHgNHu2AeA93fH5x0NJxlO8vE5h25idprlGwBVtQu4H5iuql/Oc4k3Ah/tNlPPnONTzN4EnXtTVFp2flJUTUnSA95VVe5AroOOI3RJaoQjdElqhCN0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1Ij/BbJT+A8STy0iAAAAAElFTkSuQmCC",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Boxplot를 이용한 시각화 \n",
    "df_iris.boxplot(column='Sepal.Width')\n",
    "plt.title('')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 40,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<AxesSubplot:ylabel='Sepal.Width'>"
      ]
     },
     "execution_count": 40,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAADtCAYAAACyL3KyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAARNklEQVR4nO3df4xlZX3H8fd3ZygsBTQOW6UDurFjatCIyLRRaawi24yIa1Ih+gfs0GLWtLo7iokVmqCSGGPSqOxi1A1oZ9VYWtBmobi6CFh/QZ3FhRWX2oldiluUYRb54a7o7H77xz3bDMPs3DvLPffO3ef9Sm7m3nvOPfMZwsxnn/OcH5GZSJLKtazbASRJ3WURSFLhLAJJKpxFIEmFswgkqXAWgSQVrvYiiIi+iPhRRNw8z7JLImIqInZUj3fWnUeS9HT9HfgeY8Au4KTDLL8+M9/TgRySpHnUWgQRcSrwZuCjwGXt2ObJJ5+cK1eubMemJKkY27dvfyQzV8y3rO4RwaeADwAnLrDO2yLidcBPgfdl5oMLbXDlypVMTEy0L6EkFSAiHjjcstrmCCLifODhzNy+wGo3ASsz8xXANmD8MNtaGxETETExNTVVQ1pJKledk8VnA6sjYjfwT8A5EfGl2Stk5nRmPlW9vBY4a74NZeamzBzOzOEVK+Yd2UiSjlBtRZCZl2fmqZm5EngHcFtmXjR7nYg4ZdbL1TQmlSVJHdSJo4aeJiKuAiYycwuwPiJWAzPAXuCSTueRpNJ15ISyzLwjM8+vnl9ZlcChUcPLMvOMzHxDZt7fiTxSHaanp1m/fj3T09PdjiItimcWS20yPj7Ozp072bx5c7ejSItiEUhtMD09zdatW8lMtm7d6qhAPcUikNpgfHycgwcPAnDgwAFHBeopFoHUBrfeeiszMzMAzMzMsG3bti4nklpnEUhtcO6559Lf3zgIr7+/n1WrVnU5kdQ6i0Bqg9HRUZYta/w69fX1sWbNmi4nklpnEUhtMDAwwMjICBHByMgIAwMD3Y4ktazjJ5RJR6vR0VF2797taEA9xyKQ2mRgYIANGzZ0O4a0aO4akqTCWQSSVDiLQJIKZxFIUuEsAkkqnEUgSYWzCKQ28X4E6lUWgdQm3o9AvcoikNrA+xGol1kEUht4PwL1MotAagPvR6BeZhFIbeD9CNTLLAKpDbwfgXqZRSC1gfcjUC+zCKQ2Wb16Nccffzxvectbuh1FWhSLQGqTLVu2sG/fPm666aZuR5EWxSKQ2sDzCNTLLAKpDTyPQL3MIpDawPMI1MssAqkNPI9AvcwikNrA8wjUyywCqQ08j0C9rL/bAaSjxejoKLt373Y0oJ5T+4ggIvoi4kcRcfM8y46NiOsjYjIi7oqIlXXnkeoyMDDAhg0bHA2o53Ri19AYsOswyy4FHs3MIeCTwMc7kEeSNEutRRARpwJvBq49zCpvBcar5zcAb4yIqDOTJOnp6p4j+BTwAeDEwywfBB4EyMyZiHgMGAAeqTmX2mTjxo1MTk52O8aSsGfPHgAGBwe7nGRpGBoaYt26dd2OoRbUNiKIiPOBhzNzexu2tTYiJiJiYmpqqg3ppPbbv38/+/fv73YMadEiM+vZcMTHgIuBGeA44CTgq5l50ax1vgF8ODN/EBH9wC+AFblAqOHh4ZyYmKgls/RsjI2NAXD11Vd3OYn0TBGxPTOH51tW24ggMy/PzFMzcyXwDuC22SVQ2QKMVs8vqNapp5kkSfPq+HkEEXEVMJGZW4DrgC9GxCSwl0ZhSJI6qCNFkJl3AHdUz6+c9f5vgAs7kUGSND8vMSFJhbMIJKlwFoEkFc4ikKTCWQSSVDiLQJIKZxFIUuEsAkkqnEUgSYWzCCSpcBaBJBXOIpCkwlkEklQ4i0CSCmcRSFLhLAJJKpxFIEmFswgkqXAWgSQVziKQpMJZBJJUOItAkgpnEUhS4SwCSSqcRSBJhbMIJKlwFoEkFc4ikKTCWQSSVDiLQJIKZxFIUuEsAkkqnEUgSYVruQgioi8i/jAiXnjo0WT94yLiPyLinoi4LyI+Ms86l0TEVETsqB7vPJIfQpJ05PpbWSki1gEfAn4JHKzeTuAVC3zsKeCczHwyIo4BvhsRX8/MO+esd31mvmeRuSVJbdJSEQBjwB9n5nSrG87MBJ6sXh5TPXJx8SRJdWt119CDwGOL3Xi1O2kH8DCwLTPvmme1t0XEvRFxQ0ScdpjtrI2IiYiYmJqaWmwMSdICFhwRRMRl1dOfAXdExL/R2OUDQGZ+YqHPZ+YB4JUR8VzgaxHx8sz88axVbgK+kplPRcS7gHHgnHm2swnYBDA8POyoQpLaqNmI4MTq8T/ANuD3Zr13QqvfJDN/BdwOjMx5fzozDxXLtcBZrW5TktQeC44IMvMjABFxYWb+y+xlEXHhQp+NiBXA7zLzVxGxHFgFfHzOOqdk5kPVy9XArkXmlyQ9S63OEVze4nuznQLcHhH3Aj+kMUdwc0RcFRGrq3XWV4eW3gOsBy5pMY8kqU2azRG8CTgPGIyIDbMWnQTMLPTZzLwXOHOe96+c9fxymheKJKlGzQ4f/V9gO43dNttnvf8E8L66QkmSOqfZHME9wD0R8eXM/F2HMkmSOqjZrqGdVCeBRcQzlmfmQmcWS5J6QLNdQ+dXX99dff1i9fUiPEtYko4KzXYNPQAQEasyc/bE799FxN3AB+sMJ0mqX6uHj0ZEnD3rxWsX8VlJ0hLW6kXnLgU+HxHPAQJ4FPjr2lJJkjqmpSLIzO3AGVURkJmLvgCdJGlpanbU0EWZ+aVZF5879D7Q/KJzkqSlr9mI4PerryfWHaSXbNy4kcnJyW7H0BJz6P+JsbGxLifRUjM0NMS6deu6HeOwmhXBLyPiDw5dfE4Nk5OT7PjxLg4c/7xuR9ESsuy3jSOqt//sl11OoqWkb9/ebkdoqlkRXAR8OiL2Ad8Hvgd8f849BYp04Pjnsf+l53U7hqQlbvn9t3Q7QlMLHgKamRdk5iDwF8A3aNyjeLy64fzS/+kkSU21etTQf0fEscDy6nFc9VWS1OOaHTV0BfAaYAXwn8CdwDXA2uo2lJKkHtdsRLAG+DWNewt/H7jLcwgk6ejS7FpDL42I5wGvBV4PfDAiTgDuoTFp/IX6I0qS6tR0jiAz9wI3R8RWGjeXfx3wLhqXmLAIJKnHNZsjWE1jNHA28DLgPhqHkL6fxq4iSVKPazYiuITGH/4PANsz87e1J5IkdVSzOYK/7FQQSVJ3HPE9BSJiUzuDSJK649ncXOZzbUshSeqaIy6C6h4FkqQe1+yooZtY4Cb1mbm67YkkSR3V7Kihf+hICklS1zQ7aujbnQoiSeqOlq4+GhEvAT4GnE7jyqMAZOaLa8olSeqQVieLvwB8BpgB3gBsBr5UVyhJUue0WgTLM/NbQGTmA5n5YeDN9cWSJHVKS7uGgKciYhnwXxHxHmAPcEJ9sSRJndLqiGAMOB5YT+MKpBcDo3WFkiR1Tqu3qvwhQDUqWJ+ZTzT7TEQcB/w7cGz1fW7IzA/NWedYGvMNZwHTwNszc/difgBJ0rPT0oggIoYjYidwL7AzIu6JiLOafOwp4JzMPAN4JTASEa+es86lwKOZOQR8Evj4otJLkp61VucIPg/8bWZ+ByAi/ozGkUSvONwHMjOBJ6uXx1SPuWcpvxX4cPX8BuCaiIjqs0vWnj176Nv3GMvvv6XbUSQtcX37ptmzZ6bbMRbU6hzBgUMlAJCZ36VxKOmCIqIvInYADwPbMvOuOasMAg9W25wBHgMG5tnO2oiYiIiJqampFiNLklrR6ojg2xHxOeArNP5V/3bgjoh4FUBm3j3fhzLzAPDKiHgu8LWIeHlm/nixITNzE7AJYHh4uOujhcHBQX7xVD/7X3pet6NIWuKW338Lg4PP73aMBbVaBGdUXz805/0zaRTDOQt9ODN/FRG3AyPA7CLYA5wG/Dwi+oHn0Jg0liR1SKtHDb1hsRuOiBXA76oSWA6s4pmTwVtoHIb6A+AC4LalPj8gSUebVo8aen5EXBcRX69enx4Rlzb52CnA7RFxL/BDGnMEN0fEVRFx6PLV1wEDETEJXAZ88Mh+DEnSkWp119A/0jhK6O+r1z8Frqfxh3xemXkvjV1Hc9+/ctbz3wAXtphBklSDVo8aOjkz/xk4CP9/hM+B2lJJkjqm1SL4dUQMUJ0HUJ0Y9lhtqSRJHdPqrqHLaEzs/lFEfA9YQWNyV5LU4xYcEUTEn0TEC6rzBP4cuILGpSO+Cfy8A/kkSTVrtmvoc8Bvq+evpTFZ/GngUaoTvCRJva3ZrqG+zNxbPX87sCkzbwRurC4dIUnqcc1GBH3VGb8AbwRum7Ws1fkFSdIS1uyP+VdoXGfoEWA/cOjqo0N41JAkHRUWLILM/GhEfIvGWcLfnHX5h2XAurrDSZLq13T3TmbeOc97P60njiSp09zPf4T69u31xjR6mmW/eRyAg8ed1OUkWkr69u0Fjo7LUGuWoaGhbkfQEjQ52biV99CLl/YvvTrt+Uv+b4ZFcATWrXN6RM80NjYGwNVXX93lJNLitHqtIUnSUcoikKTCWQSSVDiLQJIKZxFIUuEsAkkqnEUgSYWzCCSpcBaBJBXOIpCkwlkEklQ4i0CSCmcRSFLhLAJJKpxFIEmFswgkqXAWgSQVziKQpMJZBJJUuNqKICJOi4jbI+InEXFfRIzNs87rI+KxiNhRPa6sK48kaX513rx+Bnh/Zt4dEScC2yNiW2b+ZM5638nM82vMIUlaQG0jgsx8KDPvrp4/AewCBuv6fpKkI9OROYKIWAmcCdw1z+LXRMQ9EfH1iHjZYT6/NiImImJiamqqzqiSVJzaiyAiTgBuBN6bmY/PWXw38KLMPAPYCPzrfNvIzE2ZOZyZwytWrKg1rySVptYiiIhjaJTAlzPzq3OXZ+bjmflk9fwW4JiIOLnOTJKkp6vzqKEArgN2ZeYnDrPOC6r1iIg/rfJM15VJkvRMdR41dDZwMbAzInZU710BvBAgMz8LXAD8TUTMAPuBd2Rm1phJkjRHbUWQmd8Fosk61wDX1JVBktScZxZLUuEsAkkqnEUgSYWzCCSpcBaBJBXOIpCkwlkEklQ4i0CSCmcRSFLhLAJJKpxFIEmFswgkqXAWgSQVziKQpMJZBJJUOItAkgpnEUhS4SwCSSpcnfcsVgE2btzI5ORkt2MsCYf+O4yNjXU5ydIwNDTEunXruh1DLbAIpDZZvnx5tyNIR8Qi0LPiv/ik3uccgSQVziKQpMJZBJJUOItAkgpnEUhS4SwCSSqcRSBJhbMIJKlwFoEkFc4ikKTCWQRSm0xPT7N+/Xqmp6e7HUValNqKICJOi4jbI+InEXFfRDzjkozRsCEiJiPi3oh4VV15pLqNj4+zc+dONm/e3O0o0qLUOSKYAd6fmacDrwbeHRGnz1nnTcBLqsda4DM15pFqMz09zdatW8lMtm7d6qhAPaW2IsjMhzLz7ur5E8AuYHDOam8FNmfDncBzI+KUujJJdRkfH+fgwYMAHDhwwFGBekpH5ggiYiVwJnDXnEWDwIOzXv+cZ5YFEbE2IiYiYmJqaqq2nNKRuvXWW5mZmQFgZmaGbdu2dTmR1LraiyAiTgBuBN6bmY8fyTYyc1NmDmfm8IoVK9obUGqDc889l/7+xu09+vv7WbVqVZcTSa2rtQgi4hgaJfDlzPzqPKvsAU6b9frU6j2pp4yOjrJsWePXqa+vjzVr1nQ5kdS6Oo8aCuA6YFdmfuIwq20B1lRHD70aeCwzH6ork1SXgYEBRkZGiAhGRkYYGBjodiSpZXXeqvJs4GJgZ0TsqN67AnghQGZ+FrgFOA+YBPYBf1VjHqlWo6Oj7N6929GAek5kZrczLMrw8HBOTEx0O4Yk9ZSI2J6Zw/Mt88xiSSqcRSBJhbMIJKlwFoEkFa7nJosjYgp4oNs5pMM4GXik2yGkebwoM+c9I7fnikBayiJi4nBHZkhLlbuGJKlwFoEkFc4ikNprU7cDSIvlHIEkFc4RgSQVziKQpMJZBJJUOItAkgpnEUhS4f4P6Rb6cFTGMhwAAAAASUVORK5CYII=",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Seaborn를 이용한 Boxplot 시각화\n",
    "sns.boxplot(y='Sepal.Width', data=df_iris)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 41,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Text(0.5, 1.0, '')"
      ]
     },
     "execution_count": 41,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAAEcCAYAAAA4BiRaAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAclElEQVR4nO3de5hcVZnv8e8vnZCEJAYQbIlcWscRQ4IgNHI4ME7HMIwHdJwz+oh5wBHImIk68YJ6EgwzwGifQw7jBaMOBhtIBDIoyoyTeBjQdIE3EMJFQ1p8HAgQQAG5mMYkJuE9f+zVTKWTTld3VaW6V/0+z1NPV+29au1316p6e9Xau9ZWRGBmZnkY0+gAzMysdpzUzcwy4qRuZpYRJ3Uzs4w4qZuZZcRJ3cwsI07qNmSSQtJrGx1HI0nqkLRxD+tH7Wsk6UxJNzc6DhseJ/VRTNIGSZsl9Up6VtJqSYc2Oq4+ks6W9MNGxzGaSdpH0mclbUztvEHSF+q5zYi4NiJOrec2rH6c1Ee/t0fEZOBg4DfA0gbHUzeSxjY6hgY4H2gH3gRMATqAuxsZkI1sTuqZiIgtwA3AkX3LJE2VtELSU5IelnSBpDGSDkg9v7encpMl/UrSX6fHV0u6XNItkjZJulXS4bvb7h62MR24HDgx9TCfG+D5r5Z0W9rO9yR9WdI1aV1bGsaYK+kRYE2q+4K0rSfTtqem8rsMiaSe7Snp/kWSbpB0fdre3ZKOLis7TdK30r48JOnDZesmptflWUnrgeMraJbTJD0o6WlJl6bY95H0jKSjyup+haTfSzpoN3UcD9wYEY9HYUNErOi3f+dLWp9iu0rShLL1b5N0r6TnJP1Y0hvK1h0q6dtpf38r6Utp+U7fsCS9Pr0XnpH0gKR3l607LW17k6THJH2igtfF6ikifBulN2ADcEq6vy+wHFhRtn4F8G8UPbw24JfA3LTuVODXwCuAK4Abyp53NbAJeDMwHrgM+GHZ+gBeW8E2zi5/3gD78BPgn4B9gJOB3wHXpHVtaVsrgEnAROBc4FfAa4DJwLeBr6fyHcDGPbxGFwHbgHcB44BPAA+l+2OAtcA/pFheAzwI/Hl67iXAD4ADgEOBdf231W+7AXSn8oel1+Vv0rqvAEvKyn4E+PcB6rkAeAT4IHAUoN3s37oU0wHAj4DPpHVvBJ4ETgBagPel8uPT4/uAz6fXdgJwcv92S+seBc4BxqY6nwaOTOufAP4k3d8fOLbRn4tmvzU8AN+qaLziA9oLPJeS1ePAUWldC/CHvg9fWva3QKns8VLg58BjwMvLll8N/EvZ48nADuDQ9DiA1w62DQZJ6inZbQf2LVt2Dbsm9deUrf8+8MGyx0ekfR9LZUn99rJ1Y/qSUkp8j/R77vnAVen+g8Bby9bN67+tfs+NfuU/CHw/3T+BIlErPb4LePcA9bQAH6JI1ltTG7+v3/7NL3t8GvCf6f4/A5/uV98DwJ8CJwJPAWN3s82X2g04A/hBv/VfBS5M9x9Jbf6yRn8efCtuHn4Z/f4yIvaj6Gn9HXCrpFcCB1L0QB8uK/sw8Kqyx8uAmcDVEfHbfvU+2ncnInqBZ4Bp/cpUso09mQY8ExG/3912B1g2bTfbGwu0VrjN8v16EdiY6jwcmJaGKZ5Lw0WfKqt3Wr84ymMYdFup/LS03TuA3wMdkl5P8Q/yO7urICJ2RMSXI+IkYD+gE7gyDW/tcTtpnz7eb58OTesPBR6OiO2D7MPhwAn96jgTeGVa/06KfyQPp2G6Ewepz+rMST0T6cP/bYoe9ckUX5G3UXwo+xxG0StHUgtFUl8BfFC7nn730lk0kiZTfLV/vF+ZPW6Dore6J08AB0jad3fbLd+9svuP72Z72ykOEr9AMQzVF3cL0H+cuny/xgCHpDofBR6KiP3KblMi4rSyWMtjO2yQfeu/L4ex8+u3HDgLeC/F0NeWwSqLiM0R8WXgWcqOnexhO48Cnf32ad+IWJnWHabBDz4/Ctzar47JEfGBFNOdEfEOimG8fwW+Mdh+WH05qWdChXdQjGv2RMQOig9Yp6Qp6UDneRTDG1D0QoNijPpSYEVKgn1Ok3SypH2AT1MMW+zUi65gG78BDkl17CIiHqYYergoHUA8EXj7ILu6EvhYOsA6GfjfwPWpx/lLYIKk0yWNoxiPHt/v+cdJ+quUzD5KMaRxO/BTYJOkhemgaIukmZL6Doh+Azhf0v6SDgEWDBInwCdT+UMpxs2vL1t3DfA/KRL7it09GUDSR9MB4ImSxkp6H8Xxi3vKin1I0iGSDgAWl23nCmC+pBPS+2NSem2mpP19ArgkLZ8g6aTdhLAKeJ2k90oal27HS5qe2uxMSVMjYhvF8ZAXK3hdrJ4aPf7j2/BvFOOpmynG1TdRHDA7s2z9/hTJ4ymKHtc/UPwjP46it9d3sLOFYsx2cXp8NcWZK7ekum8DXl1Wb/mB0t1uI63bB1hNMXTz9AD78EcUByA3UYyXLwO60rq2tK2xZeXHpG08mrZ5DbB/2fqzKZLVkxQHQjew85j6DRRJbxNFYjy27LnTKP5p/Dq9Prez84HoFRTHL9YDn2TwMfUPU4zF/xb4LNDSr8z3UnzaQz3zKA7gPp+2/VPgbf3eA+enmJ6j+AZQfozircCdad0TwDeBKWndYRS9699SfOv6YtlrWH5g/IjUjk+lsmuAY1L73pReq9+l7Zzc6M9Fs9/6DtSYvUTS1RQJ64IGbPt64BcRcWEd6r6I4p/RWbWuezgkXQk8Xs3rLGkDxVk136tZYDaqNeOPOWwEScMbz1CcWngq8A6K0wezJqkN+CuKUwTNasZj6tZorwRKFMM8XwQ+EBH37PEZo5ykT1MMlV0aEQ81Oh7Li4dfzMwy4p66mVlGnNTNzDLipG5mlhEndTOzjDipm5llxEndzCwjTupmZhlxUjczy4iTuplZRuoy98uBBx4YbW1t9ah6xHjhhReYNGlSo8OwGnBb5qUZ2nPt2rVPR8Turmlbn6Te1tbGXXfdVY+qR4xSqURHR0ejw7AacFvmpRnaU9KAV97y8IuZWUYGTeqSjpB0b9ntd5I+uhdiMzOzIRp0+CUiHqC4yknfNR8fA26sb1hmZjYcQx1+mQ38ZxTXljQzsxFmqAdK30NxDcddSJpHcT1FWltbKZVK1UU2wvX29ma/j83CbZmXZm/Pii+Ska4I/zgwIyJ+s6ey7e3t4bNfbLRwW+alGdpT0tqIaN/duqEMv/wP4O7BErqZmTXOUJL6HAYYejEzs5GhojF1SZOAPwP+tr7hmJkNTFJN6sn52swV9dQj4oWIeHlEPF/vgMzMBhIRg94OX7hq0DI58y9Kzcwy4qRuZpYRJ3Uzs4w4qZuZZcRJ3cwsI07qZmYZcVI3M8uIk7qZWUac1M3MMuKkbmaWESd1M7OMOKmbmWXESd3MLCNO6mZmGXFSNzPLiJO6mVlGnNTNzDLipG5mlhEndTOzjDipm5llxEndzCwjTupmZhlxUjczy4iTuplZRipK6pL2k3SDpF9I6pF0Yr0DMzOzoRtbYbnLgJsi4l2S9gH2rWNMZmY2TIMmdUlTgTcDZwNExB+AP9Q3LDMzG45Khl9eDTwFXCXpHklfkzSpznGZmdkwVDL8MhY4FlgQEXdIugxYBPx9eSFJ84B5AK2trZRKpRqHOrL09vZmv4/Nwm2Zn2Zuz0qS+kZgY0TckR7fQJHUdxIRy4BlAO3t7dHR0VGrGEekUqlE7vvYLNyWmblpdVO356DDLxHxa+BRSUekRbOB9XWNyszMhqXSs18WANemM18eBM6pX0hmZjZcFSX1iLgXaK9vKGbWzI6++Gae37ytJnW1LVpd1fOnThzHfReeWpNY9rZKe+pmZnX1/OZtbLjk9KrrqcUxkmr/KTSSpwkwM8uIk7qZWUac1M3MMuKkbmaWESd1M7OMOKmbmWXESd3MLCNO6mZmGXFSNzPLiH9RamYjwpTpizhq+S4TwA7P8mpjAaj+162N4KRuZiPCpp5LPE1ADXj4xcwsI07qZmYZcVI3M8uIk7qZWUac1M3MMuKkbmaWESd1M7OMOKmbmWXESd3MLCNO6mZmGXFSNzPLiJO6mVlGKprQS9IGYBOwA9geEe31DMrMzIZnKLM0zoqIp+sWiVmdSKpJPRFRk3psYDWbHfGm6uqZOnFcbeJoAE+9a9kbLBm3LVpdkylfrTq1aoNmb89Kx9QDuFnSWknz6hmQmZkNX6U99ZMj4jFJrwBukfSLiLitvEBK9vMAWltbKZVKtY10hOnt7c1+H5uJ2zIvzdyeFSX1iHgs/X1S0o3Am4Db+pVZBiwDaG9vj2qvPDLS1eLqKjZC3LTabZmTJm/PQYdfJE2SNKXvPnAqsK7egZmZ2dBV0lNvBW5MZxCMBa6LiJvqGpWZmQ3LoEk9Ih4Ejt4LsZiZWZX8i1Izs4w4qZuZZcRJ3cwsI07qZmYZcVI3M8uIk7qZWUac1M3MMuKkbmaWEU+9a6Pa0RffzPObt1VdTy3m8Z46cRz3XXhq1fWYVcNJ3Ua15zdvq3ru7FpNzlazCzyYVcHDL2ZmGXFP3cxGjUovTagle16f86UJ3VM3s1EjIga9dXd3D1omZ07qZmYZcVI3M8uIk7qZWUZ8oNRGtSnTF3HU8kXVV7S8FrEAVHd6pVm1nNRtVNvUc4nPUzcr4+EXM7OMOKmbmWXESd3MLCNO6mZmGXFSNzPLiJO6mVlGnNTNzDJScVKX1CLpHkmr6hmQmZkN31B66h8BeuoViJmZVa+ipC7pEIrfP3+tvuGYmVk1Kp0m4AvA/wKmDFRA0jxgHkBrayulUqna2Ea03t7e7PdxtKjJz/Nvqr6OSePwe2IEaPbP5qBJXdLbgCcjYq2kjoHKRcQyYBlAe3t71GIujZGsVvOFWHU2dFRfR9ui1VXPH2MjR7N/NisZfjkJ+AtJG4B/Ad4i6Zq6RmVmZsMyaFKPiPMj4pCIaAPeA6yJiLPqHpmZmQ2Zz1M3M8vIkOZTj4gSUKpLJGZmVjX31M3MMuKkbmaWESd1M7OMOKmbmWXESd3MLCNO6mZmGXFSNzPLiJO6mVlGnNTNzDLipG5mlhEndTOzjDipm5llxEndzCwjTupmZhlxUjczy4iTuplZRpzUzcwyMqQrH5mNRpIGL7Nk8HoiogbRmNWXe+qWvYjY4627u3vQMk7oNlo4qZuZZcRJ3cwsI07qZmYZcVI3M8uIk7qZWUYGTeqSJkj6qaT7JN0v6eK9EZhZva1cuZKZM2cye/ZsZs6cycqVKxsdklnVKjlPfSvwlojolTQO+KGk/xcRt9c5NrO6WblyJYsXL6arq4sdO3bQ0tLC3LlzAZgzZ06DozMbvkF76lHoTQ/HpZtP2rVRrbOzk66uLmbNmsXYsWOZNWsWXV1ddHZ2Njo0s6pU9ItSSS3AWuC1wJcj4o7dlJkHzANobW2lVCrVMMyRp7e3N/t9zFlPTw87duygVCq91JY7duygp6fH7TrKNftns6KkHhE7gGMk7QfcKGlmRKzrV2YZsAygvb09Ojo6ahzqyFIqlch9H3M2ffp0Wlpa6OjoeKktu7u7mT59utt1lGv2z+aQzn6JiOeAbuCtdYnGbC9ZvHgxc+fOpbu7m+3bt9Pd3c3cuXNZvHhxo0Mzq8qgPXVJBwHbIuI5SROBPwMqmP7IbOTqOxi6YMECenp6mD59Op2dnT5IaqNeJcMvBwPL07j6GOAbEbGqvmGZ1d+cOXOYM2dO039dt7wMmtQj4mfAG/dCLGZmViX/otTMLCNO6mZmGXFSNzPLiJO6mVlGnNTNzDLipG5mlhEndTOzjDipm5llxEndzCwjTupmZhlxUjczy4iTuplZRpzUzcwy4qRuZpYRJ3Uzs4w4qZuZZcRJ3cwsI07qZmYZcVI3M8uIk7qZWUac1M3MMuKkbmaWESd1M7OMOKmbmWVk0KQu6VBJ3ZLWS7pf0kf2RmBmZjZ0Yysosx34eETcLWkKsFbSLRGxvs6xmZnZEA3aU4+IJyLi7nR/E9ADvKregZmZ2dANaUxdUhvwRuCOukRjZmZVqWT4BQBJk4FvAR+NiN/tZv08YB5Aa2srpVKpVjGOKJdddhmrV69m27ZtjBs3jtNPP52PfMSHGUaz3t7ebN+vzajZ27OipC5pHEVCvzYivr27MhGxDFgG0N7eHh0dHbWKccRYsGABq1atYsmSJRx55JGsX7+ehQsXcsghh7B06dJGh2fDVCqVyPH92qyavT0rOftFQBfQExGfq39II9cVV1zBkiVLOO+885gwYQLnnXceS5Ys4Yorrmh0aGZmQGVj6icB7wXeIunedDutznGNSFu3bmX+/Pk7LZs/fz5bt25tUERmZjur5OyXH0aEIuINEXFMun13bwQ30owfP57LL798p2WXX34548ePb1BEZmY7q/hAqcH73/9+Fi5cCMCRRx7J5z73ORYuXLhL793MrFGc1Ieg72Dopz71KbZu3cr48eOZP3++D5Ka2YjhuV+GaOnSpWzZsoXu7m62bNnihG5mI4qTuplZRpzUzcwy4jH1ARSn51cvImpSj5lZJdxTH0BE7PF2+MJVg5ZxQjezvc1J3cwsI07qZmYZacox9aMvvpnnN2+rup62Raurev7UieO478JTq47DzKxPUyb15zdvY8Mlp1dVRy1mgqv2n4KZWX9NmdSnTF/EUcsXVV/R8mrjAKjun4uZWbmmTOqbei5xT93MsuQDpWZmGXFSNzPLSFMOv0CNhj5uqv7sFzOzWmrKpF7teDoU/xRqUY+ZWS15+MXMLCNO6mZmGXFSNzPLiJO6mVlGmvJAaSUqmU9dSwavx9Pvmtne5J76AAaaH/26665jxowZjBkzhhkzZnDdddd5PnUzGzHcUx+ClStXsnjxYrq6utixYwctLS3MnTsXgDlz5jQ4OjOzCnrqkq6U9KSkdXsjoJGss7OTrq4uZs2axdixY5k1axZdXV10dnY2OjQzM6Cy4ZergbfWOY5Roaenh40bNzJz5kxmz57NzJkz2bhxIz09PY0OzcwMqGD4JSJuk9S2F2IZ8aZNm8bChQu59tprXxp+OfPMM5k2bVqjQzMzA3ygdMj6H/z0wVAzG0lqdqBU0jxgHkBrayulUqlWVY8Yjz/+OAsXLuTcc8/lkUce4bDDDuOcc85hyZIlWe5vs+jt7XX7ZaTp23NPp+OVnZbXBqyrpGxEcNxxx0WOZsyYEWvWrImIiO7u7oiIWLNmTcyYMaOBUVm1+trS8tAM7QncFQPkXw+/DMHixYuZO3cu3d3dbN++ne7ububOncvixYsbHZqZGVDB8IuklUAHcKCkjcCFEdFV78BGor5z0RcsWEBPTw/Tp0+ns7PT56ib2YhRydkvzlhl5syZw5w5c2pyjVIzs1rz8IuZWUac1M3MMuKkbmaWESd1M7OMOKmbmWVEUYefuUt6Cni45hWPLAcCTzc6CKsJt2VemqE9D4+Ig3a3oi5JvRlIuisi2hsdh1XPbZmXZm9PD7+YmWXESd3MLCNO6sO3rNEBWM24LfPS1O3pMXUzs4y4p25mlhEn9QpIOluSr1mXEUn/KOmUYTyvQ9KqesRkIGmapBuG8bzvStpvkDLDavPRxsMvFZBUAj4REXc1OharnCRRvMdfrGGdHRTvhbdVWH5sRGyv1fablV/HyjVtT13SJEmrJd0naZ2kMyQdJ+lWSWsl/YekgyW9C2gHrpV0r6SJkmZLukfSzyVdKWl8qvMSSesl/UzSP6Vlb5d0Ryr/PUmtjdzv0Si9rh8qe3yRpE9I+qSkO9PrfXFa1ybpAUkrgHXAoZKuTm38c0kfS+WuTm2LpOMl/Ti9F34qaYqkCZKuSs+5R9Ks3cR1gKR/Tdu/XdIbyuL7uqQfAV/fCy/RqLSHdl2XHp8t6TuS1gDfl7SvpG+kz9iN6XPVnspukHRgav8eSVdIul/SzZImpjKDtXmbpB9Iujvd/nsDXpbqDXRJpNxvwDuBK8oeTwV+DByUHp8BXJnul4D2dH8C8CjwuvR4BfBR4OXAA/zXt5/90t/9y5b9DfDZRu/7aLsBbwRuLXu8HngfxVkOouicrALeTHHpxReB/5bKHgfcUvbcvna5GngXsA/wIHB8Wv4yiusMfLys/V8PPJLavgNYlZYvpbhoDMBbgHvT/YuAtcDERr92I/k2QLv+CenSmcDZwEbggPT4E8BX0/2ZwPayz+UGil+StqXlx6Tl3wDOqrDN9wUmpGV/zB4uGTeSbzW78PQo9HPgs5KWUCSEZyneKLcU39ppAZ7YzfOOAB6KiF+mx8uBDwFfArYAXWnMtW/c9RDgekkHU7yZHqrP7uQrIu6R9Ip0XOMgirY6CjgVuCcVm0zxQXwEeDgibk/LHwReI2kpsBq4uV/1RwBPRMSdaVu/A5B0MkXSJiJ+Ielh4HX9nnsyReeAiFgj6eWSXpbWfSciNle/9/kaoF0f7Vfsloh4Jt0/GbgsPXedpJ8NUPVDEXFvur+WItGXG6jNJwFfknQMsINd23tUaNqkHhG/lHQscBrwGWANcH9EnDjM+rZLehMwm6I38HcUvbelwOci4jtpPPai6qNvSt+keF1fCVwPHA78n4j4ankhSW3AC32PI+JZSUcDfw7MB94NnLsX4n1h8CLGru3a33Bex61l93cAEyt83seA3wBHU3z72zKMbTdcM4+pTwN+HxHXAJcCJwAHSToxrR8naUYqvgmYku4/ALRJem16/F7gVkmTgakR8V2KN8fRaf1U4LF0/3313KfMXQ+8hyIBfBP4D+Dc9Loj6VWSXtH/SZIOBMZExLeAC4Bj+xV5ADhY0vGp/BRJY4EfAGemZa8DDktly5WX6QCe7uv1WcX6t+ue/IjinzKSjqT4tjYcA7X5VIoe/IsUn+uWYdbfUE3bU6d4Q1wq6UVgG/ABirG4L0qaSvHafAG4n2Is7nJJm4ETgXOAb6Y3wp3A5cABwL9JmkAxznte2s5FqeyzFN8GXr03di43EXG/pCnAYxHxBPCEpOnAT9JwWS9wFkXPrNyrgKsk9XVgzu9X7x8knQEsTQfUNgOnAF8B/lnSzyneF2dHxNa0rT4XAVemYYDf43/aQ9a/XdM3rYF8BVguaT3wC4rP5vPD2Oae2vxbkv4auIlR+m3LpzSa2aggqQUYFxFbJP0R8D3giIj4Q4NDG1GauaduZqPLvkC3pHEU34Y/6IS+K/fUzcwy0rQHSs3McuSkbmaWESd1M7OMOKnbqCZpcZrj42cq5uY5oYZ1Dzrzn9lI47NfbNRKPxR7G3BsOof8QIqpGGoiIk6rVV1me4t76jaaHUzxK86tABHxdEQ8nmbs+79phsWf9v36V9JBkr6lYmbHOyWdlJZP1n/NyPgzSe9MyzekfxRIOivVda+kr0pqSbddZoA0ayQndRvNbqaYWveXkr4i6U/L1j0fEUdRTLT2hbTsMuDzEXE8xURcX0vL/76vfES8geKXvy9Jv1w9AzgpIo6h+NXqmcAxwKsiYmba1lV12EezIfHwi41aEdEr6TiK6VpnUcyGuSitXln29/Pp/inAkWU/9X9ZmjvmFIr5R/rqfbbfpmZTTOF7Z3ruROBJ4N/Z8wyQZnudk7qNahGxg2K++1Kap6Vv/pXyX9X13R9DMc/6TrPv9ZvPZXcELI+I83dZ0ZgZIM0G5OEXG7UkHSHpj8sWHQM8nO6fUfb3J+n+zcCCsucfk+7eQjEnft/y/ftt6vvAu/pmgVRxxaPDK5gB0myvc0/dRrPJFDPt7Ucxk+KvgHkUZ8Tsn2ZP3ArMSeU/DHw5LR8L3EbRw/5MWr6OYrz8YuDbfRuJiPWSLgBuTrM9bqP4J7CZPcwAadYInvvFsiNpA8Vlzp5udCxme5uHX8zMMuKeuplZRtxTNzPLiJO6mVlGnNTNzDLipG5mlhEndTOzjDipm5ll5P8D1P4CbhPgUfQAAAAASUVORK5CYII=",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Boxplot를 이용한 시각화 \n",
    "df_iris.boxplot(column='Petal.Length', by='Species')\n",
    "plt.title('')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 42,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<AxesSubplot:xlabel='Species', ylabel='Petal.Length'>"
      ]
     },
     "execution_count": 42,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXgAAAEGCAYAAABvtY4XAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8rg+JYAAAACXBIWXMAAAsTAAALEwEAmpwYAAAX60lEQVR4nO3dfZRddX3v8fcnk0BCwoMmU8RMcdRJ6EWBCAeVohTFcB0u9R9Zxd5iB9u70gfLiNTeVdZNLbLSRaul6thqSaswPlbxoaW00aQqwlWrTEiEJEgyxQQHqUyoQBJDyMO3f+w9cjLOZPbMnN/Zc/Z8XmudNXvvs8/e3zl75jO/+e19flsRgZmZVc+csgswM7M0HPBmZhXlgDczqygHvJlZRTngzcwqam7ZBdRbsmRJdHZ2ll2GmVnL2Lhx4+6IaB/ruRkV8J2dnQwMDJRdhplZy5C0a7zn3EVjZlZRDngzs4pKFvCSzpC0ue7xtKRrU+3PzMyOlqwPPiIeAlYASGoDHgW+lGp/ZmZ2tGZ10VwC/EdEjHsywMzMGqtZAf8W4DNjPSFplaQBSQPDw8NNKsfMrPqSB7yk44A3AbeP9XxErI2IWkTU2tvHvJTTzMymoBnXwXcD90XEj5uwLzNrQX19fQwODibZ9tDQEAAdHR0N33ZXVxe9vb0N326jNCPgf51xumfMzFLbv39/2SWUJmnAS1oIrAR+J+V+zKy1pWwFj2y7r68v2T5mqqQBHxH7gMUp92FmZmPzJ1nNzCrKAW9mVlEOeDOzinLAm5lVlAPezKyiHPBmZhXlgDczqygHvJlZRTngzcwqygFvZlZRDngzs4pywJuZVZQD3sysohzwZmYV5YA3M6soB7yZWUU54M3MKsoBb2ZWUQ54M7OKcsCbmVWUA97MrKIc8GZmFeWANzOrKAe8mVlFJQ14SadI+ryk70t6UNIFKfdnZmbPmZt4+x8EvhwRV0g6Djgh8f7MzCyXLOAlnQxcBFwNEBHPAs+m2p+ZmR0tZRfNi4Fh4FZJmyT9vaSFo1eStErSgKSB4eHhhOWYmc0uKQN+LnAu8JGIeAWwD/jj0StFxNqIqEVErb29PWE5ZmazS8qAHwKGIuI7+fznyQLfzMyaIFnAR8R/Aj+UdEa+6BJgW6r9mZnZ0VJfRXMN8Kn8CpqHgbcl3p+ZJdTX18fg4GDZZUzKjh07AOjt7S25kuK6uroaUm/SgI+IzUAt5T7MrHkGBwfZtHUTnFJ2JZNwJPuy6dFN5dZR1JON21TqFryZVc0pcOTiI2VXUVlz7mpcz7mHKjAzqygHvJlZRTngzcwqygFvZlZRDngzs4pywJuZVZQD3sysonwdvJkVNjQ0BE819lptG+VJGIqhhmzKR8nMrKLcgjezwjo6OhjWsD/JmtCcu+bQsbSjMdtqyFbMzGzGccCbmVWUA97MrKIc8GZmFeWANzOrKAe8mVlFOeDNzCrKAW9mVlEOeDOzinLAm5lVlAPezKyiHPBmZhXlgDczqyiPJmmV0dfXx+DgYMO3OzSUjc3d0dGYEf7qdXV10dvb2/DtJvVki40Hvzf/uqjUKop7EljamE0lDXhJO4E9wGHgUETUUu7PLIX9+/eXXcKM0dXVVXYJk7Zjxw4Ali1dVnIlBS1t3PusiGjIhsbceBbwtYjYXWT9Wq0WAwMDyeoxm4qRFnZfX1/JldhUVP34Sdo4XuO5hf7PMjOzyUgd8AGsl7RR0qqxVpC0StKApIHh4eHE5ZiZzR6pA/41EXEu0A28XdJFo1eIiLURUYuIWnt7e+JyzMxmj6QBHxGP5l8fB74EvDLl/szM7DnJAl7SQkknjkwDlwJbUu3PzMyOlvIyyVOBL0ka2c+nI+LLCfdnZmZ1kgV8RDwMnJNq+2Zmdmy+TNLMrKIKteAlHQ+8Geisf01E3JimLDMzm66iXTT/BDwFbAQOpCvHzMwapWjAd0TEG5NWYmZmDVW0D/5bks5KWomZmTXUMVvwkh4gG25gLvA2SQ+TddEIiIg4O32JZmY2FRN10VzelCps1kg1ZntKI8PNttq47S051rw11DEDPiJ2AUj6RES8tf45SZ8A3jrmC83GMTg4yPYt93H6osNll1LYcQeznsxndt5bciXFPbK3rewSbAYoepL1ZfUzktqA8xpfjs0Gpy86zOra3olXtClbM9Aqty+ylI55klXS9ZL2AGdLejp/7AEeJ7t00szMZqiJumhuAm6SdFNEXN+kmsxslkl5biblOZSZfp6jaBfN7ZLOHbXsKWBXRBxqcE1mZg2zYMGCsksoTdGA/zBwLnA/2SWSZ5EN/XuypN+LiPWJ6jOzWWAmt4JbWdEPOv0IeEV+56XzgBXAw8BK4L2JajMzs2koGvDLI2LryExEbAN+KR8S2MzMZqCiXTRbJX0E+Id8/kpgWz7K5MEklVklDQ0NsW9Pmy/jS2zXnjYWDg2VXYaVrGgL/mpgELg2fzycLzsIvK7xZZmZ2XQVasFHxH7g5vwxmj+xYoV1dHTwzKHH/EGnxNYMLGJ+R0fZZVjJit7w40LgBuBFHH3Dj5ekKcvMzKaraB/8R4F3kt3wo3UGETEzm8WKBvxTEbEuaSVmZtZQRQP+65LeB3yRulv2RcR9SaoyM7NpKxrwr8q/1uqWBfD6xpZjZmaNUvQqGl8KaWbWYgpdBy/pVEkflbQunz9T0m8XfG2bpE2S7pxOoWZmNjlFP+h0G/AV4IX5/HayDzwV8Q7gwUlVZWZm01a0D35JRHxO0vUAEXFI0oSXS0rqAP4X8GfAdVMv06rkkb2tNVTBj3+atYNOPeFIyZUU98jeNpaXXYSVrmjA75O0mOzEKpJeTTYe/EQ+APxf4MTxVpC0ClgFcPrppxcsx1pVV1dX2SVM2rP5DSPmdy4ruZLiltOa77U1VtGAvw64A3ippG8C7cAVx3qBpMuBxyNio6SLx1svItYCawFqtVoUrMdaVCuO+z1Sc19fX8mVmE1O0ato7pP0K8AZZDf8eAh4E9kNQMZzIfAmSZcB84GTJH0yIq6aZs1mZlZA0ZOsRMShiNgaEVsi4iDw/gnWvz4iOiKiE3gL8DWHu5lZ8xQO+DGoYVWYmVnDFe2DH0vh/vKIuAu4axr7MjOzSTpmwEt6gLGDXMCpSSoyM7OGmKgFf3lTqjAzs4Y7ZsBHxK5mFWJmZo015ZOsktY2shAzM2us6VxFc0vDqjAzs4abcsBHxMZGFmJmZo010VU0/8wxLoeMiDc1vCIzM2uIia6i+cumVGFmZg030VU032hWIWZm1liFPskqaRlwE3Am2cBhAETESxLVZWZm01T0JOutwEeAQ8DrgI8Dn0xVlJmZTV/RgF8QEV8FFBG7IuIGsjs1mZnZDFV0sLEDkuYAOyT9AfAo0Dr3XDMzm4WKtuDfAZwA9ALnAVcBv5mqKDMzm76iAd8ZEXsjYigi3hYRbwZ8A1UzsxmsaMBfX3CZmZnNEBN9krUbuAxYKqn+jsMnkV1RY2ZmM9REJ1l/BAyQ3WC7fuyZPcA7UxVlNhV9fX0MDg42fLs7duwAoLe3t+Hb7urqSrJdM5j4k6zfA74n6dP5uqdHxENNqcxshliwYEHZJZhNSdHLJN9INi7NccCLJa0AbvRgYzaTuCVsdrSiJ1lvAF4JPAkQEZuBFyepyMzMGqJowB+MiKdGLRt3GGEzMytf0S6arZL+N9CWDzzWC3wrXVlmZjZdRVvw1wAvAw4AnwaeAq5NVJOZmTXAMQNe0nxJ1wLvBR4BLoiI8yNidUQ804wCzcq2e/durrnmGp544omySzGblIla8P1ADXgA6GYSd3jK/zh8V9L3JG2V9J5p1GlWmv7+fu6//376+/vLLsVsUiYK+DMj4qqIuAW4ArhoEts+ALw+Is4BVgBvlPTqqZVpVo7du3ezbt06IoJ169a5FW8tZaKAPzgyERGTGpogMnvz2Xn5w1feWEvp7+8nIvuxPXLkiFvx1lImCvhzJD2dP/YAZ49MS3p6oo1LapO0GXgc2BAR3xljnVWSBiQNDA8PT+mbMEtlw4YNHDyYtXMOHjzI+vXrS67IrLhjBnxEtEXESfnjxIiYWzd90kQbj4jDEbEC6ABeKenlY6yzNiJqEVFrb2+f8jdilsLKlSuZN28eAPPmzePSSy8tuSKz4opeJjktEfEk8HWyIQ/MWkZPTw+SAJgzZw49PT0lV2RWXLKAl9Qu6ZR8egGwEvh+qv2ZpbBkyRK6u7uRRHd3N4sXLy67JLPCin6SdSpOA/oltZH9IflcRNyZcH9mSfT09LBz50633q3laOQKgZmgVqvFwMBA2WWYmbUMSRsjojbWc03pgzczs+ZzwJuZVZQD3sysohzwZmYV5YA3M6soB7yZWUU54M3MKsoBb2ZWUQ54M7OKcsCbmVWUA97MrKIc8GZmFeWANzOrKAe8mVlFOeDNzCrKAW9mVlEOeDOzinLAm5lVlAPezKyiHPBmZhXlgDczqygHvJlZRTngzcwqygFvZlZRyQJe0i9K+rqkbZK2SnpHqn2ZmdnPm5tw24eAP4yI+ySdCGyUtCEitiXcp5mZ5ZK14CPisYi4L5/eAzwILE21PzMzO1pT+uAldQKvAL4zxnOrJA1IGhgeHm5GOU23fft2uru7GRwcLLsUM5tFkge8pEXAF4BrI+Lp0c9HxNqIqEVErb29PXU5pVizZg379u3jxhtvLLsUM5tFkga8pHlk4f6piPhiyn3NVNu3b2fnzp0A7Ny50614M2ualFfRCPgo8GBE/FWq/cx0a9asOWrerXgza5aULfgLgbcCr5e0OX9clnB/M9JI6328eTOzVJJdJhkR/x9Qqu23is7OzqNCvbOzs7RazGx28SdZE1u9evVR8+9+97tLqsTMZhsHfGLLly//Wau9s7OTrq6ucgsys1nDAd8Eq1evZuHChW69m1lTpRyqoOX09fUluYxxaGiIBQsW0NfX1/BtA3R1ddHb25tk22bWuhzwTbB///6ySzCzWcgBXydVK3hku6la8GZmY3EfvJlZRTngzcwqqiW7aFKdDE1lx44dQLouoFR88tastbVkwA8ODrLpgW0cOeH5ZZdSiJ4NADb+x3+WXElxc376X2WXYGbT1JIBPzQ0BETZZRQW808qu4QpiPx9NrNW5T54M7OKaskWfEdHBz8+MJdnzry87FIqa/62O+noeEHZZZjZNLgFb2ZWUS3ZgofsJOD8bXeWXUYheia7U2Er9cVnJ1ndgjdrZS0Z8K02IuOOHXsAWPbSVgrMF7Tc+2xmR2vJgG+1a7M9VIGZlcF98GZmFeWANzOrKAe8mVlFtWQffCqpxrhJPRaNx4wxs7G4Bd8Exx9/PAcOHODgwYNll2Jms4hb8HVStYJvvvlm7rjjDpYtW8Z1112XZB9mZqO5BZ/Y7t27WbduHRHBunXreOKJJ8ouycxmCQd8Yv39/Rw5cgSAw4cP09/fX3JFZjZbJAt4SR+T9LikLan20Qo2bNjAoUOHADh06BDr168vuSIzmy1StuBvA96YcPst4bWvfe1R8xdddFFJlZjZbJMs4CPibsC3BTIzK0npffCSVkkakDQwPDxcdjkNd8899xw1f/fdd5dUiZnNNqUHfESsjYhaRNTa29vLLqfhVq5cydy52dWoc+fO5dJLLy25IjObLUoP+Krr6elhzpzsbW5ra6Onp6fkisxstnDAJ7ZkyRK6u7uRRHd3N4sXLy67JDObJVJeJvkZ4NvAGZKGJP12qn3NdD09PZx99tluvZtZUykiyq7hZ2q1WgwMDJRdhplZy5C0MSJqYz3nLhozs4pywJuZVZQD3sysohzwZmYVNaNOskoaBnaVXUciS4DdZRdhU+bj19qqfPxeFBFjfkp0RgV8lUkaGO9Mt818Pn6tbbYeP3fRmJlVlAPezKyiHPDNs7bsAmxafPxa26w8fu6DNzOrKLfgzcwqygFvZlZRDvhEJF0t6YVl12FTJ+lGSW+YwusulnRnippmI0kvlPT5KbzuXyWdMsE6UzrGrcJ98IlIugt4V0R4eMwZTJLIfg+ONHCbF5Md+8sLrj83Ig41av+zhd+3ibkFPwmSFkr6F0nfk7RF0pWSzpP0DUkbJX1F0mmSrgBqwKckbZa0QNIlkjZJekDSxyQdn2/zzyVtk3S/pL/Ml/2qpO/k6/+bpFPL/L5bQf4+vr1u/gZJ75L0R5Luzd/f9+TPdUp6SNLHgS3AL0q6LT+mD0h6Z77ebfmxRNL5kr6VH/vvSjpR0nxJt+av2STpdWPU9XxJ/5jv/98lnV1X3yckfRP4RBPeopZwjOO4JZ+/WtIdkr4GfFXSCZI+l/8OfSn/vanl6+6UtCQ/3g9K+jtJWyWtl7QgX2eiY9wp6R5J9+WPXy7hbZm6iPCj4AN4M/B3dfMnA98C2vP5K4GP5dN3AbV8ej7wQ2B5Pv9x4FpgMfAQz/0ndUr+9Xl1y/4PcHPZ3/tMfwCvAL5RN78N6CG7PE5kjZk7gYuATuAI8Op83fOADXWvHTkOtwFXAMcBDwPn58tPAuYCf1h3vH8JeCQ/1hcDd+bLPwT8aT79emBzPn0DsBFYUPZ7N5Me4xzH1wJb8vmrgSHg+fn8u4Bb8umXA4fqfu92kg1R0JkvX5Ev/xxwVcFjfAIwP1+2DBgo+z2azCO7G7QV9QBws6S/IAuLn5D9UG3I/tOnDXhsjNedAfwgIrbn8/3A24G/Bp4BPpr32Y7023YAn5V0GtkP3g/SfDvVERGbJP1Cft6jnezYnAVcCmzKV1tE9kv6CLArIv49X/4w8BJJHwL+BVg/avNnAI9FxL35vp4GkPQasgAnIr4vaRewfNRrX0PWMCAiviZpsaST8ufuiIj90//uq2Oc4/jDUattiIj/yqdfA3wwf+0WSfePs+kfRMTmfHojWejXG+8YLwT+WtIK4DA/f3xnNAf8JETEdknnApcBa4CvAVsj4oIpbu+QpFcCl5C1Iv6ArJX3IeCvIuKOvD/3hulXPyvcTvY+vgD4LPAi4KaIuKV+JUmdwL6R+Yj4iaRzgP8J/C7wa8BvNaHefROvMiuNPo6jTeV9O1A3fRhYUPB17wR+DJxD9l/gM1PYd2ncBz8JeavipxHxSeB9wKuAdkkX5M/Pk/SyfPU9wIn59ENAp6SufP6twDckLQJOjoh/JftBOid//mTg0XzaN3It7rPAW8jC4XbgK8Bv5e8zkpZK+oXRL5K0BJgTEV8AVgPnjlrlIeA0Sefn658oaS5wD/Ab+bLlwOn5uvXq17kY2D3SOrRxjT6Ox/JNsj/ISDqT7L+2qRjvGJ9M1rI/QvZ72zbF7ZfCLfjJOQt4n6QjwEHg98j69voknUz2fn4A2ErWt/e3kvYDFwBvA27Pf2juBf4WeD7wT5Lmk/UTX5fv54Z83Z+Q/Zfw4mZ8c60uIrZKOhF4NCIeAx6T9D+Ab+ddaHuBq8hacPWWArdKGmnwXD9qu89KuhL4UH5ybj/wBuDDwEckPUD2c3B1RBzI9zXiBuBjedfBT/Ef7AmNPo75f1zj+TDQL2kb8H2y372nprDPYx3jL0j6TeDLtNh/Xb5M0sxalqQ2YF5EPCPppcC/AWdExLMllzYjuAVvZq3sBODrkuaR/Rf8+w7357gFb2ZWUT7JamZWUQ54M7OKcsCbmVWUA94qTdL/y8cfuV/ZuECvauC2Jxyt0KxMvorGKiv/ANrlwLn59elLyIZ+aIiIuKxR2zJLwS14q7LTyD45egAgInZHxI/yUQbfm48C+d2RTxhLapf0BWWjT94r6cJ8+SI9N2rk/ZLenC/fmf/RQNJV+bY2S7pFUlv++LlRKs2axQFvVbaebCjg7ZI+LOlX6p57KiLOIhvw7QP5sg8C74+I88kGCPv7fPmfjKwfEWeTfbr4Z/JPy14JXBgRK8g+KfsbwApgaUS8PN/XrQm+R7NxuYvGKisi9ko6j2y42deRjdD5x/nTn6n7+v58+g3AmXVDDZyUj2PzBrKxUUa2+5NRu7qEbMjhe/PXLgAeB/6ZY49SaZaUA94qLSIOk43Nf1c+ZszIWDD1n/AbmZ5DNkb8USMGjhpbZiwC+iPi+p97opxRKs0Ad9FYhUk6Q9KyukUrgF359JV1X7+dT68Hrql7/Yp8cgPZ+P0jy583aldfBa4YGalS2V2cXlRglEqzpNyCtypbRDY64Clkoz0OAqvIrqx5Xj7C4wHg1/P1e4G/yZfPBe4ma3mvyZdvIetffw/wxZGdRMQ2SauB9fmIlAfJ/iDs5xijVJql5rFobNaRtJPstm67y67FLCV30ZiZVZRb8GZmFeUWvJlZRTngzcwqygFvZlZRDngzs4pywJuZVdR/A8cG4CWbR2lWAAAAAElFTkSuQmCC",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Seaborn를 이용한 Boxplot 시각화\n",
    "sns.boxplot(x='Species', y='Petal.Length', data=df_iris)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 분산(Variance), 표준편차(Standard Deviation)\n",
    "\n",
    "분산과 표준편차는 평균값을 이용해 산포도를 수치화 할 수 있으며, 통계 계산시에도 평균값과 함께 사용하기 유용합니다.\n",
    "\n",
    "* 편차(Deviation): 데이터가 평균으로부터 떨어진 정도, 데이터 - 평균\n",
    "* 분산(Variance): 편차 제곱의 평균, 편차의 평균은 항상 0 이 되기 때문에 분산을 이용함\n",
    "* 표준편차(Standard Deviation): 분산의 제곱근, 분산은 제곱값으로 수가 너무 크고, 단위가 변하기(예, $m$ -> $m^2$)때문에 표준편차를 이용함\n",
    "\n",
    "![](https://mechanicalbase.com/wp-content/uploads/2020/11/image.png)\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 43,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Sepal.Length   0.68569\n",
       "Sepal.Width    0.18998\n",
       "Petal.Length   3.11628\n",
       "Petal.Width    0.58101\n",
       "dtype: float64"
      ]
     },
     "execution_count": 43,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# 분산\n",
    "df_iris.var()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 44,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Sepal.Length   0.82807\n",
       "Sepal.Width    0.43587\n",
       "Petal.Length   1.76530\n",
       "Petal.Width    0.76224\n",
       "dtype: float64"
      ]
     },
     "execution_count": 44,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "# 표준편차\n",
    "df_iris.std()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### 변동계수(Coefficient of Variation)\n",
    "\n",
    "변동계수(CV)는 표준편차를 평균으로 나눈 값으로 두 집단에서 데이터의 흩어짐 정도를 비교하는데 사용합니다.  \n",
    "\n",
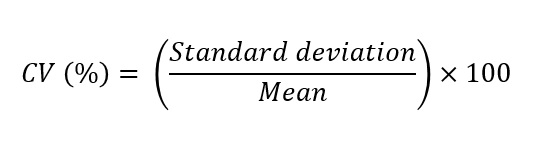    "![](https://toptipbio.com/wp-content/uploads/2017/04/Coefficient-of-variation-CV-formula.jpg)\n",
    "\n",
    "예를 들어 두 회사의 연도별 수익률에 대하여 어느 회사가 변동폭이 큰지를 비교할때 사용해볼 수 있습니다.\n",
    "\n",
    "![](https://exceltable.com/en/analyses-reports/images/analyses-reports11-1.png)\n",
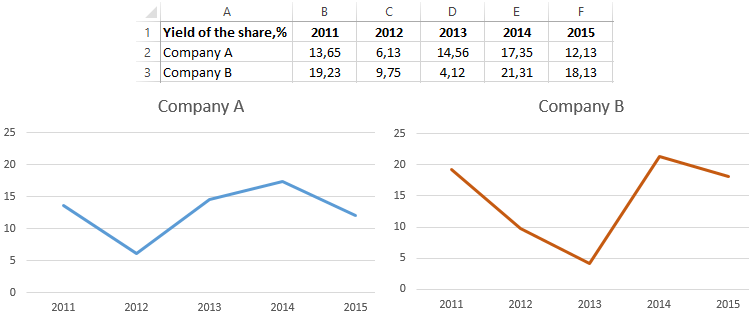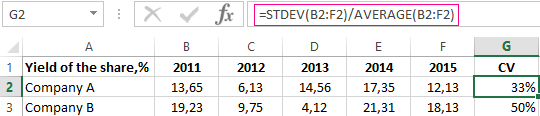    "![](https://exceltable.com/en/analyses-reports/images/analyses-reports11-2.png)\n",
    "\n",
    "https://exceltable.com/en/analyses-reports/coefficient-variation-in-excel"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 45,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "mean1: 5.84, mean2: 3.76\n",
      "cv1: 0.14, cv2: 0.47\n"
     ]
    }
   ],
   "source": [
    "# Scipy 를 통한 CV 계산\n",
    "# https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.variation.html\n",
    "mean1 = df_iris['Sepal.Length'].mean()\n",
    "mean2 = df_iris['Petal.Length'].mean()\n",
    "cv1 = sp.stats.variation(df_iris['Sepal.Length'])\n",
    "cv2 = sp.stats.variation(df_iris['Petal.Length'])\n",
    "print(f\"mean1: {mean1:.2f}, mean2: {mean2:.2f}\")\n",
    "print(f\"cv1: {cv1:.2f}, cv2: {cv2:.2f}\")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3.8.9 64-bit ('skp-n4e-jupyter-sts')",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.8.9"
  },
  "nikola": {
   "category": "",
   "date": "2019-02-24",
   "description": "",
   "link": "",
   "slug": "ml-descriptive-statistics",
   "tags": "",
   "title": "Machine Learning - Descriptive Statistics",
   "type": "text"
  },
  "toc": {
   "base_numbering": 1,
   "nav_menu": {},
   "number_sections": true,
   "sideBar": true,
   "skip_h1_title": false,
   "title_cell": "Table of Contents",
   "title_sidebar": "Contents",
   "toc_cell": false,
   "toc_position": {},
   "toc_section_display": true,
   "toc_window_display": false
  },
  "vscode": {
   "interpreter": {
    "hash": "074780be484a97690bb59ec71f684629e06fa9a846f324f8f10540b41bb15945"
   }
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}